يبدو أن النموذج الإحصائي الجديد يقوض الافتراضات المقبولة منذ فترة طويلة من نظرية الأعداد. إلى أي مدى يمكنك الوثوق بها إذا كان الدليل الدقيق فقط هو المهم حقًا؟
في الآونة الأخيرة ، توصل أربعة باحثين إلى نموذج يقلب رأساً على عقب الحس السليم الكامل لمجال بحثهم. استخدموا البيانات الحسابية للإشارة إلى أن وجهة النظر السائدة لعدة عقود لأحد المفاهيم الأساسية كانت خاطئة.
وهؤلاء ليسوا علماء أحياء أو علماء مناخ أو فيزيائيين. في مجالها العلمي ، ليس للنماذج التجريبية رأي فيما يتعلق بالحقيقة. إنهم علماء رياضيات ، ممثلون عن الانضباط ، الذين عادة ما تحفظهم عملتهم القياسية - وهي دليل منطقي لا يمكن إنكاره - من المناقشات التي تؤثر على مجالات أخرى. ومع ذلك ، هم هنا ، مع نموذجهم الذي يقول إنه ربما حان الوقت لمراجعة بعض الأفكار الراسخة.
نموذج
منشور على الإنترنت في عام 2016 وجاهز للظهور في مجلة الجمعية الرياضية الأوروبية ينتمي إلى هذا المفهوم الرياضي الموقر مثل رتبة معادلة جبرية. الترتيب هو مقياس يتوافق مع عدد حلول المعادلة التي تتعلق بالأرقام العقلانية ، وأيها غير منطقي. المعادلات ذات المستوى العالي لها حلول أكثر عقلانية وأكثر تعقيدًا.
منذ بداية القرن العشرين ، اهتم علماء الرياضيات بمسألة ما إذا كانت هناك قيود على ارتفاع رتبة المعادلة. في البداية ، اعتقد الجميع تقريبًا أنه يجب أن يكون التقييد موجودًا. لكن بحلول السبعينيات ، تغير الرأي السائد - بدأ معظم علماء الرياضيات يعتقدون أن الرتبة كانت غير محدودة ، مما يعني أنه من الممكن اكتشاف المنحنيات ذات الرتب الكبيرة بشكل لا نهائي. لذلك حدث ذلك ، على الرغم من أن بعض علماء الرياضيات يعتقدون أنه لا توجد حجج قوية تدعم هذا الرأي.
"إن الناس متسلطون للغاية بشأن غياب القيود. قال
أندرو جرانفيل ، عالم الرياضيات في جامعة مونتريال وكلية لندن الجامعية: "عندما تبدأ في الفهم ، يتبين أن الأدلة على ذلك ضعيفة للغاية".
اليوم ، تشير الأدلة إلى خلاف ذلك. بعد عامين من ظهور النموذج ، أقنعت العديد من علماء الرياضيات بأن رتبة المعادلات الجبرية من نوع معين كانت محدودة حقًا. ومع ذلك ، لا يعتقد الجميع أن هذا النموذج مقنع. يثير الافتقار إلى الاتفاق أسئلة لا تتعلق غالبًا بالنتائج الرياضية - ما هو الوزن الذي يمكن أن يكون للدليل التجريبي في مجال لا يمثل فيه سوى الدليل الصارم؟
قالت
جينيفر بارك ، عالمة الرياضيات في جامعة أوهايو ، المؤلفة المشاركة في العمل: "لا يوجد مبرر رياضي أن هذا النموذج هو بالضبط ما نحتاج إليه". "بالإضافة إلى ذلك ، من وجهة نظر تجريبية ، تعمل الكثير من الأشياء."
نقطة إلى نقطة
إذا تم إعطاؤك معادلة ، يمكنك رسم منحنى لحلولها على الرسم البياني. يرغب علماء الرياضيات في معرفة عدد هذه الحلول المنطقية - فهي تنتمي إلى نوع الأرقام ، والتي يمكن التعبير عنها كنسبة من عددين صحيحين (1/2 أو -3 أو 4483/929).
يصعب العثور على حلول عقلانية بشكل منهجي ، لكن علماء الرياضيات لديهم تقنيات تعمل في ظل ظروف معينة. خذ المعادلة x
2 + y
2 = 1. الرسم البياني لحلول هذه المعادلة هو دائرة. للعثور على جميع النقاط العقلانية للدائرة ، نبدأ بحل واحد محدد - دعنا نقول ، من النقطة التي عندها x = 1 و y = 0. ثم ارسم خطًا من خلال هذه النقطة يتقاطع مع الدائرة عند نقطة أخرى. إذا كان منحدر خطنا منطقيًا ، فستكون نقطة التقاطع الثانية أيضًا حلًا عقلانيًا. من خلال رسم خط ، قمنا بزيادة عدد القرارات العقلانية من واحد إلى اثنين.
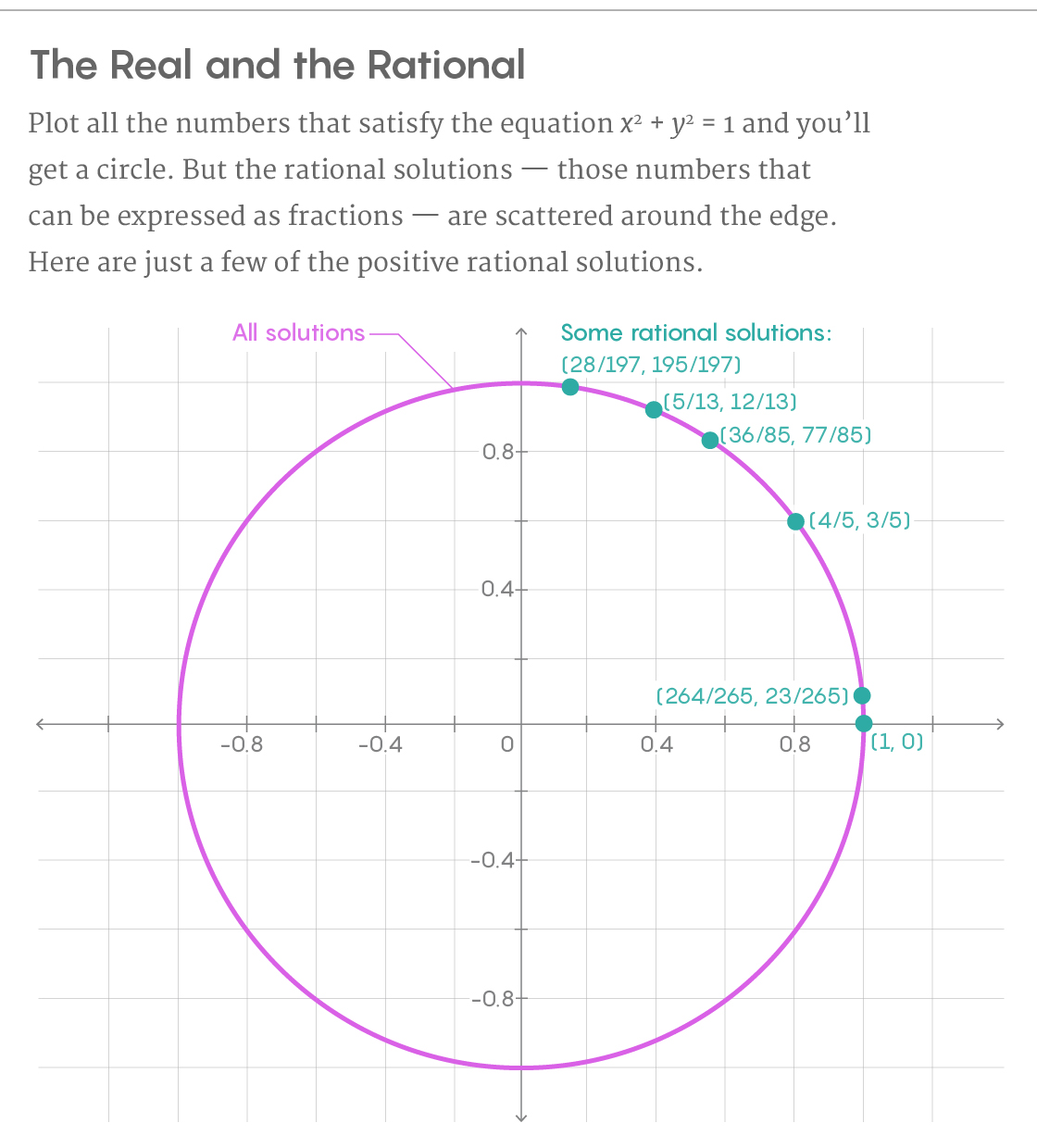
وليس هناك حاجة للتوقف عند هذا الحد. نكرر الإجراء عن طريق رسم خط مستقيم مع منحدر عقلاني آخر من خلال النقطة العقلانية الثانية - فهو يتقاطع مع الدائرة عند النقطة العقلانية الثالثة. استمرارًا بهذه الطريقة إلى اللانهاية ، سنجد في النهاية جميع النقاط العقلانية للدائرة ، التي يوجد فيها عدد لا نهائي.
وفي حالة الدائرة ، تحتاج إلى البدء من نقطة واحدة فقط ، ويمكنك العثور عليها جميعًا. يُعرف عدد القرارات العقلانية التي تحتاج إلى معرفتها في البداية للعثور على جميع القرارات الأخرى باسم رتبة المنحنى. الترتيب هو طريقة مرتبة لوصف مجموعة غير محدودة من القرارات العقلانية في رقم واحد. قال
بيورن بونين ، عالم الرياضيات في معهد ماساتشوستس للتكنولوجيا ، المؤلف المشارك للنموذج ، مع بارك ،
جون فويت من كلية دارتموث ،
وميلاني ماتشيت وود من جامعة ويسكونسن: "إنه نوع من أفضل الطرق لوصف الحلول العقلانية لهذه المنحنيات".
الدائرة هي معادلة تربيعية ، أو معادلة من الدرجة الثانية (تعني "الدرجة" حجم أكبر درجات درجات المعادلة). لأكثر من مائة عام ، عرف علماء الرياضيات كيفية إيجاد حلول عقلانية لمعادلات الدرجة الثانية.
النوع التالي من المعادلات هو المنحنيات الإهليلجية ، حيث توجد متغيرات مرفوعة إلى الدرجة الثالثة. توجد المنحنيات الناقصية في المجال الأكثر جاذبية للبحث الرياضي. إنها أكثر تعقيدًا من المعادلات من الدرجة الثانية ، لذلك فهي مثيرة للاهتمام للدراسة ، لكنها ليست معقدة للغاية. لا يزال الإجراء المتغير لرسم خطوط مستقيمة قابلاً للتطبيق على المنحنيات الناقصية ، ولكنه يتوقف عن العمل مع معادلات من الدرجة الرابعة وأعلى.
تأتي منحنيات الاهليلجيه في رتب مختلفة. مع بعض المنحنيات البيضاوية ، يمكنك البدء من نقطة عقلانية واحدة ، وتطبيق إجراء رسم الخطوط وعدم العثور على جميع الحلول العقلانية. قد تحتاج إلى إضافة نقطة عقلانية ثانية لا تتعلق بالنقطة الأولى. مع ذلك ، ستبدأ في إجراء جديد لرسم الخطوط ، وستجد توازنًا بين النقاط العقلانية. منحنى ، للعثور على جميع النقاط العقلانية التي تحتاج إلى معرفة نقطتين منطقيتين في البداية ، له رتبة تساوي نقطتين.
لا توجد قيود مثبتة على ارتفاع رتبة منحنى بيضاوي. كلما ارتفعت رتبة المعادلة ، كلما كانت مجموعة الحلول العقلانية للمنحنى أوسع وأكثر تعقيدًا. قال بونين "إن الترتيب يقيس بطريقة ما مدى تعقيد مجموعة القرارات".
ومع ذلك ، فإن الرتبة تستحيل محاولات علماء الرياضيات لوصفها نظريًا. إذا تم منحك منحنى بيضاوي الشكل ، فلن يكون له علاقة واضحة بين كيفية ظهوره ورتبته. قال بارك: "إذا كان لدي منحنى بيضاوي الشكل ، وقمت بتعديل المعاملات قليلاً ، فإن ترتيبها يتغير جذريًا". - يمكنك تغيير المعامل بمقدار واحد ، وسوف يقفز الترتيب إلى مليون. لا أحد يعرف كيف تتصرف الرتب ".
دفع عدم وجود نظرية عامة علماء الرياضيات إلى التراجع إلى مجموعة صغيرة من الأدلة التي لديهم من أجل التكهن بوجود قيود على الرتبة. قال جرانفيل: "وجهة النظر هي أنه لا توجد قيود على الرتبة ، لأن الناس في كل الأوقات وجدوا المزيد والمزيد من الرتب العالية". حامل الرقم القياسي الحالي هو منحنى بيضاوي من الدرجة 28 ، تم اكتشافه في عام 2006 من قبل نعوم الكيس ، عالم الرياضيات في جامعة هارفارد.
ولكن بعد ذلك ظهر هذا النموذج الجديد ، وذكر أنه من شبه المؤكد أنه نهاية الطريق.
مفاجأة في حوالي 21
لدراسة الظواهر المعقدة للغاية أو التي يتعذر الوصول إليها للبحث المباشر ، يستخدم العلماء النماذج. بعد إنشاء نظير لثقب أسود في المختبر ، قد يتمكنون من معرفة شيء ما حول كيفية عمل الثقوب السوداء الحقيقية ، دون الاضطرار إلى المشي على طول حافة أفق الحدث.
يفعل علماء الرياضيات نفس الشيء. مثال جيد هو دراسة الأعداد الأولية. يريد علماء الرياضيات معرفة إجابة السؤال عن
التوائم الأولية - هل هناك عدد لا نهائي من أزواج الأعداد الأولية التي تختلف عن 2 (3 و 5 و 11 و 13). تتجاوز الإجابة الشاملة معرفتهم ، لكنهم ابتكروا نماذج تتنبأ بتكرار الأرقام المزدوجة - ويبدو أن الإجابة هي أنها تحدث لعدد غير محدود من المرات.
لا يدرس النموذج الجديد بشكل مباشر المنحنيات الناقصية. تستكشف مثل هذا الشيء الرياضي مثل
قلب المصفوفة . تشير النوى إلى المنحنيات الإهليلجية ، مثل الفئران بالنسبة للناس ، فهي ليست نفس الشيء ، ولكن من الأسهل دراستها ، ويؤمل أن تكون قريبة بما يكفي لاستخلاص استنتاجات حول بعضها على أساس التجارب على الآخرين. على وجه الخصوص ، النوى لها نسختها الخاصة من
الرتبة . بعد دراسة توزيع رتب النوى - كم عدد النوى التي حصلت على رتبة 1 ، وكم نواة لها رتبة 2 ، وهكذا - يأمل أربعة من علماء الرياضيات في الحصول على فكرة عن توزيع رتب المنحنيات الإهليلجية. في الواقع ، يراهنون على أن توزيع رتب النوى والمنحنيات الإهليلجية متشابهة مع بعضها البعض.
 جنيفر بارك ، بيورن بونين وميلاني وود
جنيفر بارك ، بيورن بونين وميلاني وودقال بارك: "إن قفزة الإيمان تدخل حيز التنفيذ". "نأمل أن تكون هناك مجموعة أخرى من الأشياء الرياضية أكثر قابلية للفهم ولها نفس توزيع الرتب مثل المنحنيات البيضاوية."
عندما قام الباحثون الأربعة بهذا العمل ، اعتبر معظم علماء الرياضيات الرتبة غير محدودة. ومع ذلك ، روى النموذج قصة مختلفة. وتقول إنه لا يوجد سوى عدد محدود من المنحنيات البيضاوية برتبة تزيد عن 21. وإذا كان هناك عدد محدود منها ، فسيحصل أحدهم على أعلى رتبة - مما يعني أن الرتبة لا تزال لها حد أعلى. عندما رأى علماء الرياضيات الأربعة هذا ، أدركوا أن لديهم نتيجة حية في أيديهم.
قال وود: "هذا التنبؤ لا يتطابق مع ما آمن به الجميع ، على الأقل ما اعترف به علنا". "لا أحد يعتقد أن الرتب يمكن أن يكون لها قيود."
إذا كان الإيمان بالنموذج يتطلب خطوة جادة إلى حد ما ، فعندما يبلغ النموذج عن أن الفطرة السليمة كانت خاطئة ، يلزم اتخاذ خطوة أكبر. ومع ذلك ، فإن الكثير من الأدلة تتحدث لصالح هذه النتيجة. يعتمد هذا النموذج على نماذج سابقة أنشأها علماء رياضيون آخرون درسوا خصائص مختلفة للمنحنيات الناقصية. هذه النماذج صمدت أمام اختبار الزمن. وقد تم إثبات بعض هذه التوقعات.
قال وود: "لم يقترح أحد البدء من الصفر وصنع نموذج جديد". "كان السؤال هو كيفية إثراء النماذج الموجودة التي يؤمن بها الناس بالفعل."
سبب آخر للاعتقاد في النموذج هو أن قيمة الرتبة 21 لا تبدو أي حدود تعسفية. قبل عشر سنوات ، ابتكر Granville نموذجًا آخر ، والذي اتبعت منه أيضًا أنه يجب ألا يكون هناك سوى عدد محدود من المنحنيات البيضاوية برتبة أعلى من 21. على عكس الصدفة البسيطة من وجهة نظر العديد من علماء الرياضيات.
قال بارك: "لدينا نموذجان ارشاديان مختلفان تمامًا وكلاهما أعطانا نفس الرقم ، 21 - فاجأ الناس."
ربما كان السبب الأكثر إقناعاً أن النموذج يبدو جديرًا بالمصداقية هو حقيقة أن توقعاته الأخرى تتطابق تمامًا مع الخصائص المثبتة للمنحنيات الناقصية. ينطبق الاستنتاج المعمم للنموذج - وجود عدد محدود من المنحنيات الإهليلجية برتبة أكثر من 21 - على جميع المنحنيات الإهليلجية. ومع ذلك ، لديهم عائلات معينة ، بالنسبة لكثير من علماء الرياضيات قد حددوا بالفعل حدود الرتب. كما توقع النموذج قيم التصنيف للعديد من هذه العائلات ، وكانت تنبؤاته متشابهة ، أو حتى تزامنت تمامًا مع تلك الحدود التي حددها علماء الرياضيات بالفعل.
قال بارك: "حدودنا تنبأت بدقة بكل تلك الحالات التي درسها أشخاص آخرون". "يشك الناس في تقاريري ، ولكن عندما أذكر مصادفات أخرى ، فإنهم متفاجئون جدًا من ذلك."
بين الأدلة والأدلة
يحظى النموذج بالكثير من الدعم ، ولكن لا يؤمن به الجميع ، وقد يتبين أنه خاطئ. أهم المشككين هو نعوم الكيس ، وهو عالم رياضيات في جامعة هارفارد حقق رقمًا قياسيًا لمنحنى بيضاوي. في العقود التي تلت أن أصبح أصغر أستاذ بدوام كامل في جامعة هارفارد ، حصل على العديد من النتائج التي تشير إلى عدم وجود حدود رتبة. كتب إلي إليس بالبريد "رأيي لم يتغير لفترة طويلة - لا أعتقد أننا على دراية جيدة في هذه القضية لدعم هذه الفرضية أو تلك".
يعتقد Elkis أن النموذج قد لا يعمل بشكل صحيح في نواح كثيرة. يأخذ في الاعتبار المنحنيات المختارة عشوائيًا ، أو تكون المنحنيات متوسطة إلى حد ما. ومع ذلك ، هناك أدلة ، بما في ذلك البحث الذي قام به Elkis نفسه ، حول إمكانية وجود عائلات من المنحنيات الإهليلجية ، والتي تشتمل كل منها على عدد لا نهائي من هذه المنحنيات ، والذي يختلف سلوكه بشكل كبير عن سلوك المنحنيات النموذجية. يكتب إلكيس: "إن النماذج الإرشادية القائمة على السلوك المتوقع للمنحنيات العشوائية قد لا تروي القصة الكاملة عن السلوك المتطرف".
حتى أحد مؤلفي النموذج ليس متأكدًا تمامًا منه. قال وود: "أود أن أقول إنني محدود في الرتب مثل الملحد". تعترف بأن النموذج قد يكون غير صحيح لأسباب عبر عنها Elkis. ولكن إذا لم يتكيف النموذج مع المهمة ، فعندئذ لأنه لم يأخذ في الاعتبار بعض الخصائص المخفية وغير المتوقعة للمنحنيات الإهليلجية. "السؤال هو: إذا كنت لا تؤمن برتب محدودة ، في أي مكان يتوقف النموذج عن العمل؟" - قال وود.
"على الأرجح ، سيكونون على حق إذا لم يتوصل أحدهم إلى سبب عبقري لخطئهم. قال ألكسندر سميث ، وهو طالب دراسات عليا في جامعة هارفارد يعمل مع Elkis ويدرس صفوف المنحنيات الإهليلجية: "ليس لدي أي فكرة عما إذا كان مثل هذا السبب موجودًا أم لا".
لا يرفع مؤلفو النموذج أهميته إلى العقيدة. إنهم يعرفون الفرق بين الأدلة والأدلة ، ويفهمون أنه لن تؤدي أي جبال للأولى إلى الأخيرة. لكنهم يعتقدون أن عملهم ، على الأقل ، يوفر أساسًا معقولًا للتفكير في المفاهيم الرياضية الأساسية بعد قرن من التفكير البسيط.
قال بارك: "ربما يمثل العثور على منحنيات بيضاوية من الدرجة الأولى تحديًا لعلماء الرياضيات". أو ربما يجب على علماء الرياضيات "أن يعيدوا النظر في آرائهم حول ما آمننا به ، باعتباره فرضية شائعة".