مرحبًا. نحن ، كمسافرين في أفكارنا ، ومحللين لحالتنا ، يجب أن نفهم أين هي جيدة ، وأين يكون الأمر كذلك ، وأين نحن بالضبط ، وأريد أن أسترعي انتباه القراء إلى ذلك.
كيف نجمع سلاسل من الأفكار ، بالتتابع؟ ، بافتراض ختام كل خطوة ، والتحكم في تدفق التحكم وحالة الخلايا في الذاكرة؟ أو ببساطة من خلال وصف بيان المشكلة ، أخبر البرنامج بالمهمة المحددة التي تريد حلها ، وهذا يكفي لتجميع جميع البرامج. لا تحول الترميز إلى دفق من الأوامر التي من شأنها تغيير الحالة الداخلية للنظام ، ولكن التعبير عن المبدأ كمفهوم الفرز ، لأنه ليس عليك تخيل نوع الخوارزمية المخفية هناك ، ما عليك سوى الحصول على البيانات التي تم فرزها. ليس لشيء يمكن لرئيس أمريكا ذكر الفقاعة ، فهو يعبر عن فكرة أنه فهم شيئًا ما في البرمجة. اكتشف للتو أن هناك خوارزمية فرز ، والبيانات في الجدول على سطح المكتب ، في حد ذاتها ، لا يمكن أن تصطف ، بطريقة سحرية ، بترتيب أبجدي.
يبدو أن هذه الفكرة التي أتحدث عنها جيدًا تجاه الطريقة التصريحية للتعبير عن الأفكار ، والتعبير عن كل شيء بتسلسل الأوامر والتحولات بينهما ، قديمة وقديمة ، لأن أجدادنا فعلوا ذلك ، قام أجدادهم بتوصيل جهات الاتصال على لوحة التصحيح وحصلوا على الأضواء الوامضة ، ولدينا شاشة والتعرف على الصوت ، حيث أنه في هذا المستوى من التطور لا يزال بإمكانك التفكير في الأوامر التالية ... يبدو لي أنه إذا عبرت عن البرنامج بلغة منطقية ، فسوف تبدو أكثر قابلية للفهم ، ويمكن القيام بذلك في مجال التكنولوجيا ، تم إجراء رهان في الثمانينيات.
حسنًا ، استمرت المقدمة ...
سأحاول ، في البداية ، إعادة سرد آلية الفرز السريع. لفرز قائمة ، تحتاج إلى تقسيمها إلى قائمتين فرعيتين ودمج القائمة الفرعية المفروزة مع قائمة فرعية أخرى مرتبة .
يجب أن تكون عملية التقسيم قادرة على تحويل القائمة إلى قائمتين فرعيتين ، إحداهما تحتوي على جميع العناصر الأقل أساسية ، وتحتوي القائمة الثانية على عناصر كبيرة فقط. للتعبير عن هذا ، تم كتابة سطرين فقط على Erlang:
qsort([])->[]; qsort([H|T])->qsort([X||X<-T,X<H])++[H|qsort([X||X<-T,X>=H])].
هذه التعبيرات من نتيجة عملية التفكير مثيرة للاهتمام بالنسبة لي.
من الأصعب تقديم وصف لمبدأ الفرز بشكل حتمي. كيف يمكن أن تكون هناك ميزة لهذه الطريقة في البرمجة ، ومن ثم لا تسميها ، على الرغم من وجود s-place-place ، على الأقل fortran. هل هذا لأن جافا سكريبت ، وجميع اتجاهات وظائف لامدا في المعايير الجديدة لجميع اللغات ، هي تأكيد على إزعاج الخوارزمية.
سأحاول إجراء تجربة للتحقق من مزايا نهج واحد وآخر لاختبارها. سأحاول أن أثبت أنه يمكن مقارنة السجل التعريفي لتعريف الفرز وسجله الخوارزمي من حيث الأداء واستنتاج كيفية صياغة البرامج بشكل صحيح. ربما سيؤدي هذا إلى دفع البرمجة إلى الرف من خلال الخوارزميات وتدفق الأوامر ، كمقاربات قديمة ، ليست ذات صلة على الإطلاق للاستخدام ، لأنه لا يقل عن الموضة التعبير في Haskell أو في مقطع عرضي. وربما ليس فقط يمكن أن تعطي خرافية حادة البرامج نظرة واضحة ومدمجة؟
سأستخدم Python للتوضيح ، لأنه يحتوي على العديد من النماذج ، وهذا ليس C ++ على الإطلاق ولم يعد ليسب. يمكنك كتابة برنامج واضح في نموذج مختلف:
فرز 1
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<T])+[H]+qsort([X for X in T if X>=T])
يمكن نطق الكلمات بهذه الطريقة : يأخذ التصنيف العنصر الأول كقاعدة ، ثم يتم فرز جميع العناصر الأصغر وتوصيلها بجميع العناصر الكبيرة ، قبل فرزها .
أو ربما يعمل مثل هذا التعبير بشكل أسرع من الفرز المكتوب في شكل خرقاء لتبديل بعض العناصر القريبة أو لا. هل من الممكن التعبير عن هذا بإيجاز ، ولا يتطلب الكثير من الكلمات لذلك. حاول صياغة مبدأ الفرز حسب الفقاعة بصوت عالٍ وأخبره لرئيس الولايات المتحدة ، لأنه حصل على هذه البيانات المقدسة ، وتعلم عن الخوارزميات ووضعها ، على سبيل المثال ، على النحو التالي : من أجل فرز القائمة ، تحتاج إلى أخذ عنصرين ومقارنتهما ببعضهما البعض و إذا كان الأول أكثر من الثاني ، فيجب استبدالها وإعادة ترتيبها ، ثم تحتاج إلى تكرار البحث عن أزواج من هذه العناصر من بداية القائمة حتى انتهاء التباديل .
نعم ، مبدأ فرز الفقاعة يبدو أطول من إصدار الفرز السريع ، ولكن الميزة الثانية ليست فقط في إيجاز السجل ، ولكن أيضًا في سرعته ، فإن التعبير عن نفس الفرز السريع الذي صاغته الخوارزمية سيكون أسرع من الإصدار المعبر عنه بشكل معلن؟ ربما نحتاج إلى تغيير وجهات نظرنا حول تدريس البرمجة ، فمن الضروري كيف حاول اليابانيون إدخال تدريس مقدمة وما يرتبط بها من تفكير في المدارس. يمكنك الانتقال بشكل منظم إلى المسافة من اللغات الخوارزمية للتعبير عن الأفكار.
فرز 2
لإعادة إنتاج هذا ، كان علي أن أنتقل إلى الأدب ، هذا تصريح من هوار ، أحاول تحويله إلى بيثون:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p - 1) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo - 1 j = hi + 1 while True do: i= i + 1 while A[i] < pivot do : j= j - 1 while A[j] > pivot if i >= j: return j A[i],A[j]=A[j],A[i]
أنا معجب بالفكرة ، هناك حاجة إلى دورة لا نهاية لها هنا ، كان سيدخلها هناك)) ، كان هناك مهرجون.
تحليل
الآن دعنا نضع قائمة طويلة ونجعلها مرتبة حسب كلتا الطريقتين ، ونفهم كيفية التعبير عن أفكارنا بشكل أسرع وأكثر كفاءة. ما هو النهج الأسهل؟
إنشاء قائمة بأرقام عشوائية كمشكلة منفصلة ، هكذا يمكن التعبير عنها:
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<H])+[H]+qsort([X for X in T if X>=H]) import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=qsort(list) print('qsort='+str(monotonic() - start))
فيما يلي القياسات التي تم الحصول عليها:
>>> test(10000) qsort=0.046999999998661224 >>> test(10000) qsort=0.0629999999946449 >>> test(10000) qsort=0.046999999998661224 >>> test(100000) qsort=4.0789999999979045 >>> test(100000) qsort=3.6560000000026776 >>> test(100000) qsort=3.7340000000040163 >>>
الآن أكرر هذا في صياغة الخوارزمية:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p ) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo-1 j = hi+1 while True: while True: i=i+1 if(A[i]>=pivot) or (i>=hi): break while True: j=j-1 if(A[j]<=pivot) or (j<=lo): break if i >= j: return max(j,lo) A[i],A[j]=A[j],A[i] import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=quicksort(list,0,len-1) print('quicksort='+str(monotonic() - start))
كان علي العمل على تحويل المثال الأصلي للخوارزمية من مصادر قديمة إلى ويكيبيديا. إذن هذا: تحتاج إلى أخذ العنصر الداعم وترتيب العناصر في الصفيف الفرعي بحيث يكون كل شيء أقل وأقل على اليسار ، وأكثر وأكثر على اليمين. للقيام بذلك ، استبدل اليسار بالعنصر الأيمن. نكرر هذا لكل قائمة فرعية للعنصر المرجعي مقسومًا على الفهرس ، إذا لم يكن هناك شيء للتغيير ، فإننا ننتهي .
المجموع
دعنا نرى ما هو الفارق الزمني لنفس القائمة ، والتي يتم فرزها حسب طريقتين بدورهما. سنجري 100 تجربة وسننشئ رسمًا بيانيًا:
import random def test(len): t1,t2=[],[] for n in range(1,100): list=[random.randint(-100, 100) for r in range(0,len)] list2=list[:] from time import monotonic start = monotonic() slist=qsort(list) t1+=[monotonic() - start]
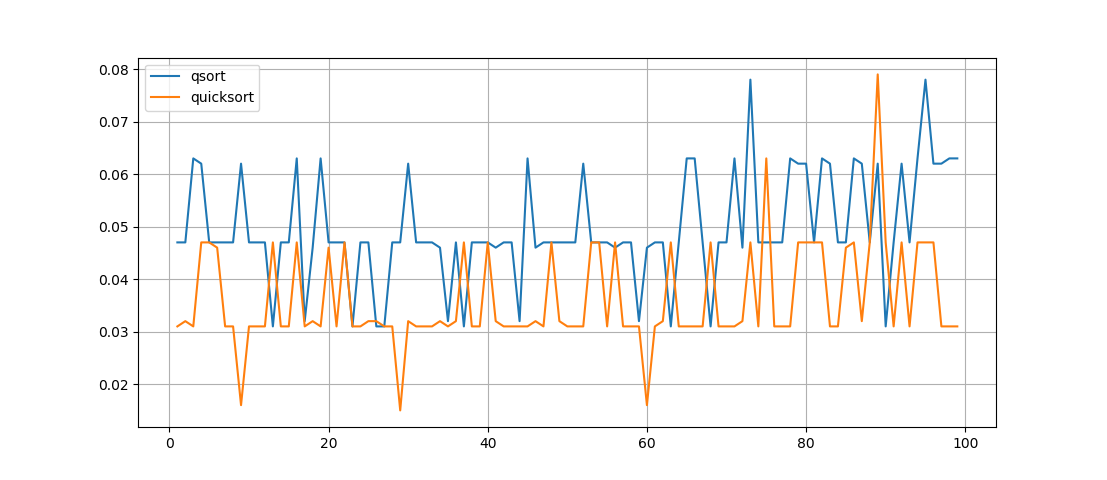
ما يمكن رؤيته هنا - تعمل وظيفة Quicksort () بشكل أسرع ، ولكن سجلها ليس واضحًا جدًا ، على الرغم من أن الوظيفة متكررة ، ولكن ليس من السهل على الإطلاق فهم عمل التباديل الذي تم إجراؤها فيه.
حسنًا ، ما هو تعبير الفكر الفردي أكثر وعياً؟
مع اختلاف بسيط في الأداء ، نحصل على مثل هذا الاختلاف في حجم وتعقيد التعليمات البرمجية.
ربما تكون الحقيقة كافية لتعلم اللغات الحتمية ، ولكن ما هو أكثر جاذبية بالنسبة لك؟
ملاحظة. وهنا مقدمة:
qsort([],[]). qsort([H|T],Res):- findall(X,(member(X,T),X<H),L1), findall(X,(member(X,T),X>=H),L2), qsort(L1,S1), qsort(L2,S2), append(S1,[H|S2],Res).