Geekly articles weekly

تتأخر ذاكرة الكمبيوتر كل 7.8 ثانية


ذاكرة DDR3 SDRAM الحديثة. المصدر: BY-SA / 4.0 من Kjerish

في زيارة حديثة لمتحف تاريخ الكمبيوتر في ماونتن فيو ، لفت انتباهي مثال قديم للذاكرة الفريتية .


المصدر: BY-SA / 3.0 من كونستانتين لانزيت

توصلت بسرعة إلى استنتاج مفاده أن ليس لدي أي فكرة عن كيفية عمل هذه الأشياء. قم بتدوير الحلقات (لا) ، ولماذا تمر ثلاثة أسلاك من خلال كل حلقة (ما زلت لا أفهم كيف تعمل). والأهم من ذلك ، أدركت أن لدي فكرة صغيرة عن كيفية عمل ذاكرة الوصول العشوائي الديناميكية الحديثة!


المصدر: دورة ذاكرة Ulrich Drapper

كنت مهتمًا بشكل خاص بأحد عواقب كيفية عمل ذاكرة الوصول العشوائي الديناميكية. اتضح أن كل بت من البيانات يتم تخزينه بشحنة (أو غيابه) على مكثف صغير في شريحة ذاكرة الوصول العشوائي. لكن هذه المكثفات تفقد شحنتها تدريجيًا بمرور الوقت. لتجنب فقدان البيانات المخزنة ، يجب تحديثها بانتظام لاستعادة الشحن (إن وجد) إلى مستواه الأصلي. تتضمن عملية التحديث هذه قراءة كل بت ثم كتابتها مرة أخرى. أثناء هذا "التحديث" ، تكون الذاكرة مشغولة ولا يمكنها إجراء عمليات عادية ، مثل الكتابة أو تخزين البتات.

لقد أزعجني هذا لفترة طويلة ، وتساءلت ... هل من الممكن ملاحظة تأخير في التحديث على مستوى البرنامج؟

قاعدة التدريب على ترقية ذاكرة الوصول العشوائي الديناميكية


تتكون كل وحدة DIMM من "خلايا" و "صفوف" و "أعمدة" و "جوانب" و / أو "صفوف". يشرح هذا العرض التقديمي من جامعة يوتا التسمية. يمكن التحقق من تكوين ذاكرة الكمبيوتر باستخدام decode-dimms . هنا مثال:

  $ فك شفرة dimms
 الحجم 4096 ميجابايت
 البنوك × الصفوف × الأعمدة × بت 8 × 15 × 10 × 64
 الرتب 2

لسنا بحاجة لفهم مخطط DDR DIMM بأكمله ، نريد أن نفهم تشغيل خلية واحدة فقط تقوم بتخزين جزء واحد من المعلومات. بتعبير أدق ، نحن مهتمون فقط بعملية التحديث.

تأمل في مصدرين:


يجب تحديث كل بت في الذاكرة الديناميكية: يحدث هذا عادةً كل 64 مللي ثانية (ما يسمى التحديث الثابت). هذه عملية مكلفة إلى حد ما. لتجنب توقف رئيسي واحد كل 64 مللي ثانية ، يتم تقسيم العملية إلى 8192 عملية تحديث أصغر. في كل واحد منهم ، يرسل جهاز التحكم في ذاكرة الكمبيوتر أوامر التحديث إلى شرائح DRAM. بعد تلقي التعليمات ، ستقوم الشريحة بتحديث 1/8192 خلية. إذا كنت تعد ، فإن 64 مللي ثانية / 8192 = 7812.5 نانوثانية أو 7.81 ميكرومتر. هذا يعني ما يلي:

  • يتم تنفيذ أمر تحديث كل 7812.5 نانوثانية. يطلق عليه tREFI.
  • تستغرق عملية التحديث والاسترداد بعض الوقت ، حتى تتمكن الشريحة من إجراء عمليات القراءة والكتابة العادية مرة أخرى. ما يسمى tRFC يساوي إما 75 ns أو 120 ns (كما هو الحال في وثائق ميكرون المذكورة).

إذا كانت الذاكرة ساخنة (أكثر من 85 درجة مئوية) ، فإن وقت تخزين البيانات في الذاكرة ينخفض ​​، وينخفض ​​وقت التحديث الثابت إلى 32 مللي ثانية. وفقا لذلك ، ينخفض ​​tREFI إلى 3906.25 نانوثانية.

شريحة الذاكرة النموذجية مشغولة بالتحديث لجزء كبير من حياتها: من 0.4٪ إلى 5٪. بالإضافة إلى ذلك ، تعد شرائح الذاكرة مسؤولة عن الحصة غير العادية من استهلاك الطاقة لجهاز الكمبيوتر النموذجي ، ويتم إنفاق معظم هذه الطاقة على الترقيات.

يتم حظر شريحة الذاكرة بالكامل أثناء التحديث. أي أن كل بت في الذاكرة مقفل لأكثر من 75 نانوثانية كل 7812 نانوثانية. دعونا قياسه.

إعداد التجربة


لقياس العمليات بدقة النانو ثانية ، تحتاج إلى دورة ضيقة جدًا ، ربما في C. يبدو كما يلي:

  for (i = 0; i < ...; i++) { //   . *(volatile int *) one_global_var; //   CPU.    _mm_clflush(one_global_var); //   ,     //    (25    160). // , - . asm volatile("mfence"); //     clock_gettime(CLOCK_MONOTONIC, &ts); }

الرمز الكامل متاح على GitHub.

الكود بسيط جدا قم بقراءة الذاكرة. نقوم بتفريغ البيانات من ذاكرة التخزين المؤقت لوحدة المعالجة المركزية. نقيس الوقت.

(ملاحظة: في التجربة الثانية ، حاولت استخدام MOVNTDQA لتحميل البيانات ، ولكن هذا يتطلب صفحة ذاكرة خاصة غير قابلة للتخزين المؤقت وحقوق الجذر).

على جهاز الكمبيوتر الخاص بي ، يعرض البرنامج البيانات التالية:

  # طابع زمني ، وقت الدورة
 3101895733 ، 134
 3101895865 ، 132
 3101896002 ، 137
 3101896134 ، 132
 3101896268 ، 134
 3101896403 ، 135
 3101896762 ، 359
 3101896901 ، 139
 3101897038 ، 137

عادة ، يتم الحصول على دورة تستغرق حوالي 140 نانوثانية ، ويقفز الوقت بشكل دوري إلى حوالي 360 نانوثانية. في بعض الأحيان تظهر نتائج غريبة على أكثر من 3200 نانوثانية.

لسوء الحظ ، فإن البيانات صاخبة للغاية. من الصعب جدًا معرفة ما إذا كان هناك تأخير ملحوظ مرتبط بدورات التحديث.

تحويل فورييه السريع


في وقت ما بزغ لي. نظرًا لأننا نريد العثور على حدث بفاصل زمني ثابت ، يمكننا إرسال البيانات إلى خوارزمية FFT (تحويل فورييه السريع) ، الذي يفك تشفير الترددات الرئيسية.

لست أول من يفكر في الأمر: مارك سيبورن مع الضعف الشهير روهامر نفذ هذه التقنية في عام 2015. حتى بعد الاطلاع على كود مارك ، كان الحصول على FFT للعمل أصعب مما توقعت. لكن في النهاية ، جمعت كل القطع معًا.

تحتاج أولاً إلى إعداد البيانات. يتطلب FFT إدخال بفاصل زمني ثابت لأخذ العينات. نريد أيضًا تقليم البيانات لتقليل الضوضاء. بالتجربة والخطأ ، وجدت أن أفضل نتيجة يتم تحقيقها بعد المعالجة الأولية للبيانات:

  • يتم قطع القيم الصغيرة (أقل من 1.8 متوسط) لتكرارات الحلقة وتجاهلها واستبدالها بالأصفار. نحن حقا لا نريد أن نصدر ضوضاء.
  • يتم استبدال جميع القراءات الأخرى بوحدات ، لأن سعة التأخير الناجم عن بعض الضوضاء ليست مهمة بالنسبة لنا.
  • لقد استقرت على فاصل زمني لأخذ العينات قدره 100 نانوثانية ، ولكن أي رقم يصل إلى تردد Nyquist (التردد المتوقع المزدوج) سيفعل .
  • يجب أخذ عينات البيانات في وقت محدد قبل تقديمها إلى FFT. جميع طرق أخذ العينات المعقولة تعمل بشكل جيد ، لقد استقرت على الاستيفاء الخطي الأساسي.

الخوارزمية شيء من هذا القبيل:

 UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )

التي تنتج في بياناتي متجهًا مملاً إلى حد ما مثل هذا:

  [0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 1 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 
  0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 1 ، 1 ، 0 ،
  0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 
  0 ، 0 ، 1 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، ...]

ومع ذلك ، فإن الناقل كبير جدًا ، وعادة ما يكون حوالي 200 ألف نقطة بيانات. مع هذه البيانات ، يمكنك استخدام FFT!

 C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)

بسيطة جدا ، أليس كذلك؟ ينتج هذا عن متجهين:

  • يحتوي C على أعداد معقدة من مكونات التردد. نحن لسنا مهتمين بالأرقام المعقدة ، ويمكنك تخفيفها باستخدام الأمر abs() .
  • يحتوي F على تسميات ، أي مدى التردد يكمن في مكان المتجه C. نقوم بتطبيع الأس إلى الهرتز عن طريق الضرب في تكرار أخذ العينات لمتجه الإدخال.

يمكن رسم النتيجة على مخطط:



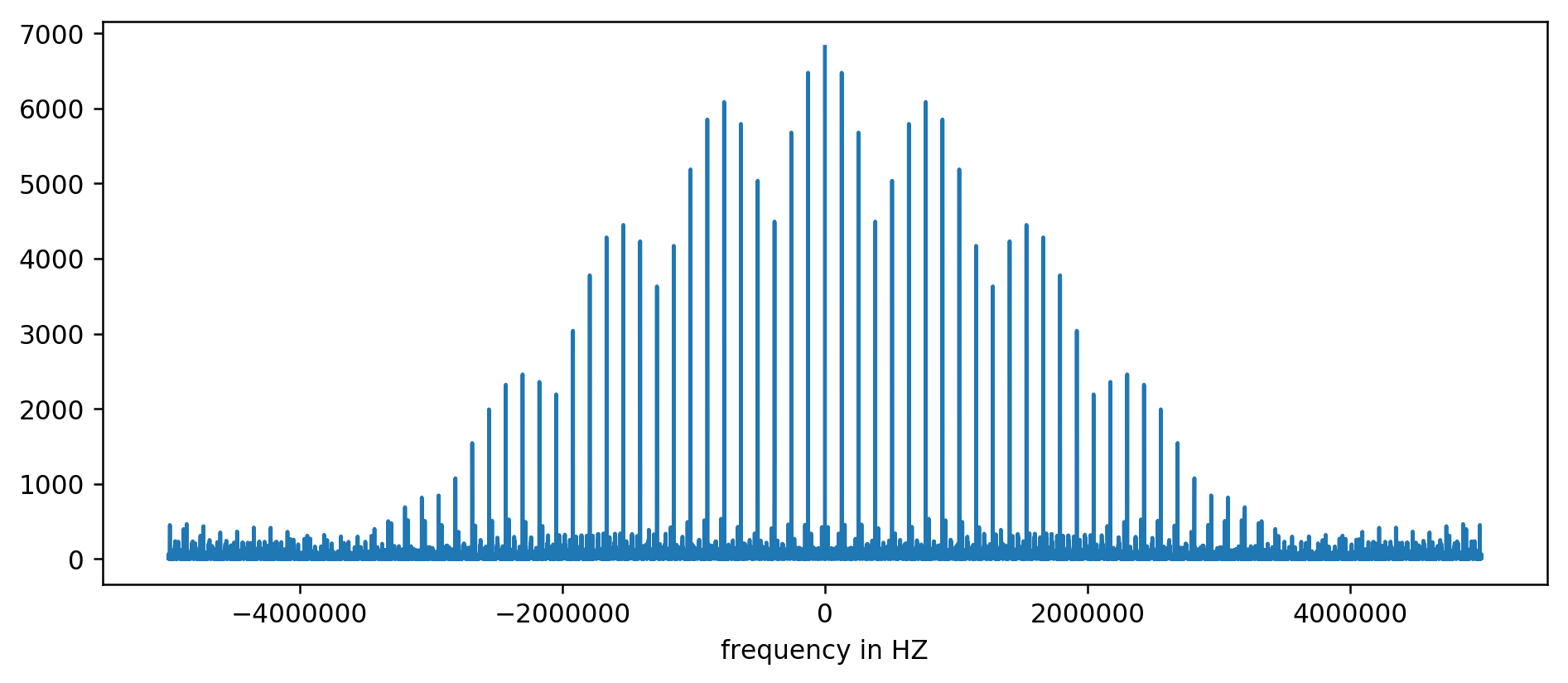
المحور Y بدون وحدات ، حيث قمنا بتطبيع وقت التأخير. على الرغم من ذلك ، تظهر الرشقات بوضوح في بعض نطاقات التردد الثابتة. دعونا نعتبرها أقرب:



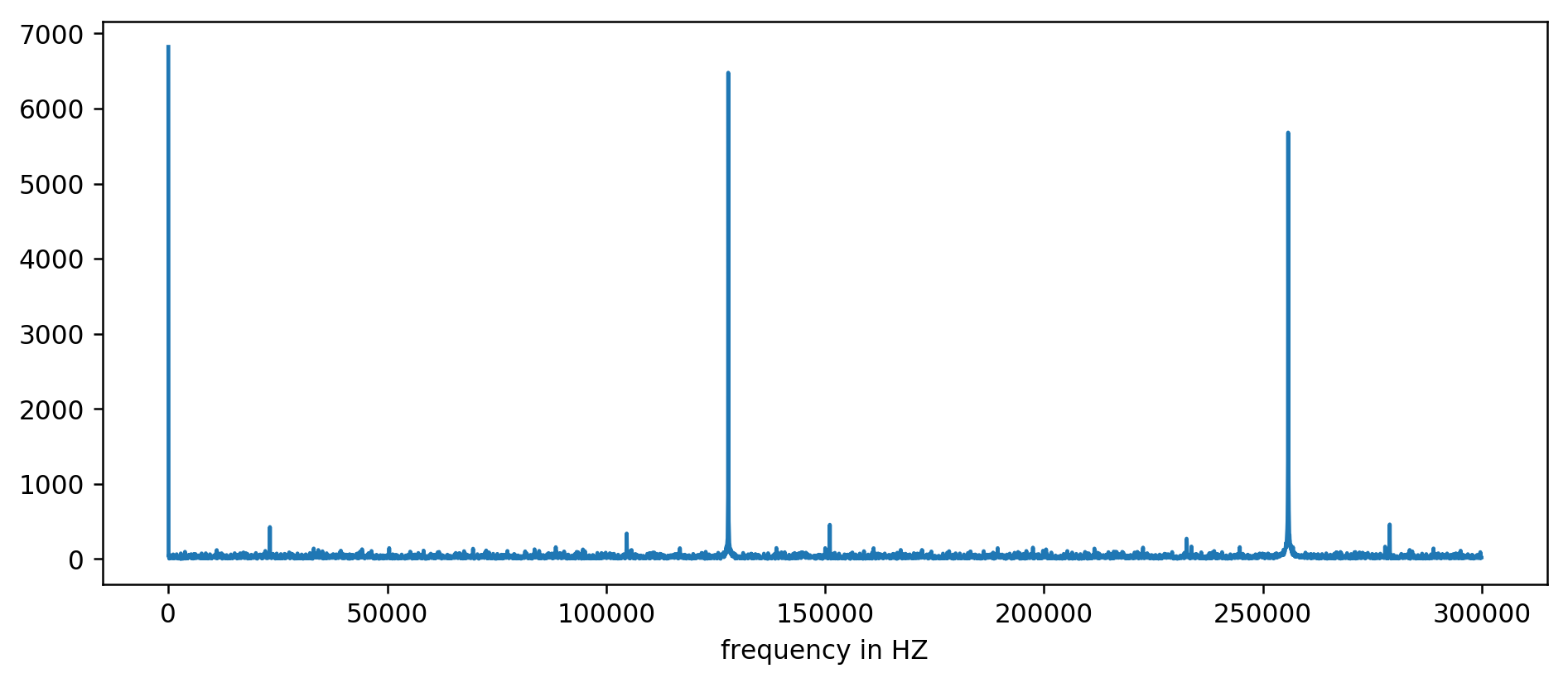
نرى بوضوح القمم الثلاثة الأولى. بعد القليل من الحساب غير المعبر ، بما في ذلك قراءة التصفية على الأقل عشرة أضعاف المتوسط ​​، يمكنك استخراج الترددات الأساسية:

  127850.0
 127900.0
 127950.0
 255700.0
 255750.0
 255800.0
 255850.0
 255900.0
 255950.0
 383600.0
 383650.0

نعتبر: 1000000000 (نانوثانية) / 127900 (هرتز) = 7818.6 نانوثانية

الصيحة! القفزة الأولى في التردد هي حقًا ما كنا نبحث عنه ، وهو يرتبط حقًا بوقت التحديث.

القمم المتبقية عند 256 كيلو هرتز ، 384 كيلو هرتز ، 512 كيلو هرتز هي ما يسمى التوافقيات التي هي مضاعفات تردد قاعدتنا 128 كيلو هرتز. هذا هو الأثر الجانبي المتوقع تمامًا لتطبيق FFT على شيء مثل الموجة المربعة .

لتسهيل التجارب ، قمنا بعمل نسخة لسطر الأوامر . يمكنك تشغيل الكود بنفسك. فيما يلي مثال على الإطلاق على الخادم الخاص بي:

  ~ / 2018-11-memory-تحديث $ جعل
 gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram
 ./measure-dram |  python3 ./analyze-dram.py
 [*] التحقق من ASLR: main = 0x555555554890 مكدس = 0x7fffffefe2ec
 [] حقيقة ممتعة.  فعلت 40663553 clock_gettime () في الثانية
 [*] قياس وقت MOVQ + CLFLUSH.  تشغيل 131072 تكرارات.
 [*] تدوين البيانات
 [*] بيانات الإدخال: min = 117 avg = 176 med = 167 max = 8172 items = 131072
 [*] مدى القطع 212-inf
 [] 127849 عنصر تحت القطع ، 0 عنصر فوق قطع ، 3223 عنصر غير الصفر
 [*] تشغيل FFT
 [*] يبلغ حجم التردد الأعلى فوق 2 كيلو هرتز أقل من 250 كيلو هرتز 7716
 [+] ارتفاع التردد الأعلى من 2 كيلو هرتز هو في:
 127906 هرتز 7716
 255813 هرتز 7947
 383720Hz 7460
 511626Hz 7141

يجب أن أعترف ، الرمز غير مستقر تمامًا. في حالة حدوث مشاكل ، يُنصح بتعطيل Turbo Boost ، وتحجيم تردد وحدة المعالجة المركزية وتحسين الأداء.

الخلاصة


هناك استنتاجان رئيسيان من هذا العمل.

لقد رأينا صعوبة تحليل البيانات منخفضة المستوى ويبدو أنها صاخبة إلى حد ما. بدلاً من التقييم بالعين المجردة ، يمكنك دائمًا استخدام FFT القديم الجيد. عند إعداد البيانات ، من الضروري ، إلى حد ما ، التفكير بالتمني.

الأهم من ذلك ، لقد أظهرنا أنه من الممكن غالبًا قياس سلوك الأجهزة الخفي من عملية بسيطة في مساحة المستخدم. أدى هذا النوع من التفكير إلى اكتشاف ثغرة Rowhammer الأصلية ، وتم تنفيذه في هجمات Meltdown / Spectre وظهر مرة أخرى في تناسخ Rowhammer الأخير لذاكرة ECC .

لا يزال هناك الكثير خارج نطاق هذه المقالة. بالكاد تطرقنا إلى التشغيل الداخلي لنظام الذاكرة الفرعي. لمزيد من القراءة ، أوصي:


أخيرًا ، إليك وصفًا جيدًا لذاكرة الفريت القديمة:

Source: https://habr.com/ru/post/ar431010/

More articles:


All Articles