يوضح دليل جديد وجود نوعين من المنحنيات اللانهائية

كشف عمل ألكسندر سميث في فرضية غولدفيلد عن الخصائص الأساسية للمنحنيات الإهليلجية

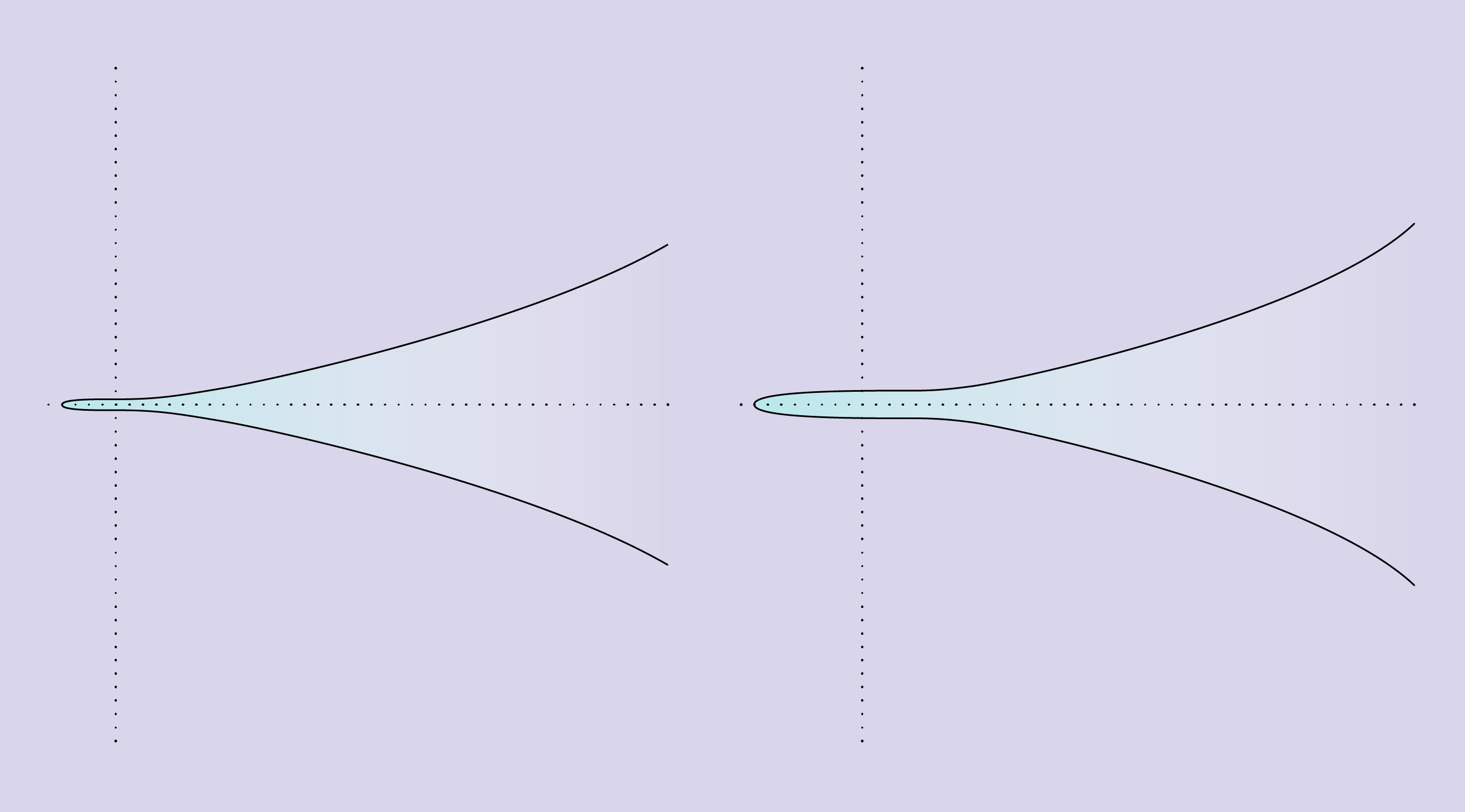يوضح منحنى إهليلجيان غرابة مفهوم الرتبة. يتم وصف المنحنى الموجود على اليسار بالمعادلة y ² = x ³ + 1 ، ويمر عبر خمس نقاط منطقية فقط ويحتل المرتبة 0. يتم وصف المنحنى الموجود على اليمين بالمعادلة y ² = x ³ + 8 ، ويمر عبر عدد لا نهائي من النقاط العقلانية ، ولديه رتبة 1.

يمكن أن يكون هناك العديد من أنواع المنحنيات الناقصية ، ولكن هناك نوعان فقط من أصنافهما الحقيقية. هذا هو نتيجة الأدلة الجديدة التي تلقاها طالب دراسات عليا من جامعة هارفارد.

تبدو المنحنيات الناقصة غريبة ، لكن هذه أشياء هندسية غير ملحوظة ، ليست أكثر تعقيدًا من الخطوط المستقيمة أو القطع المكافئ أو القطع الناقص. في عمله المنشور على الإنترنت العام الماضي ، أثبت Alexadr Smith الفرضية التي كانت سائدة قبل أربعين عامًا فيما يتعلق بالميزة الأساسية للمنحنيات الناقصة للرتبة. أثبت سميث أنه بالنسبة لعائلة معينة من المنحنيات التي لها خاصية واحدة ، فإن النصف لديه رتبة 0 والنصف الآخر لديهم رتبة 1.

تؤسس هذه النتيجة خاصية داعمة للأشياء التي شغلت علماء الرياضيات لعدة قرون ، والتي نمت أهميتها بشكل خاص في العقود الأخيرة.

"لقد كنا نفكر في ذلك لأكثر من 1000 عام ، والآن لدينا فهم احتمالي للمنحنيات الناقصية. قال شاو أو زانغ ، عالم الرياضيات في جامعة برينستون ، الذي قدم توصيات سميث بشأن عمله عندما كان لا يزال طالبًا في برينستون.

المنحنيات الاهليلجية هي معادلات ذات متغيرات مرفوعة للقوة الثالثة ، على سبيل المثال ، y ² = x ³ + 1. وقد ظهرت في العديد من البراهين الرياضية الهامة في العقود الأخيرة ، بما في ذلك أهم دليل على نظرية Fermat العظمى من عام 1994. يكمن جزء من أهميتها في حقيقة أنها تنتمي إلى النوع الأكثر تعقيدًا من معادلات كثيرات الحدود ، والتي لدى علماء الرياضيات نوعًا من الأفكار النظامية حولها.

قال دوريان غولدفيلد ، عالم الرياضيات في جامعة كولومبيا ، الذي اقترح عام 1979 فرضية حصلت على اسمه: "المنحنيات البيضاوية هي حالة مثيرة للاهتمام".

تقوم فرضية غولدفيلد بعمل تنبؤات حول رتبة المنحنيات الناقصية. كما وصفنا سابقًا في مقالة حديثة ، " ما هو الدليل الذي يمكن أن يقنع علماء الرياضيات إذا لم يكن هناك دليل صارم؟ " الترتيب هو مقياس لتعقيد مجموعة من الحلول العقلانية للمنحنى (الحلول التي يمكن تمثيلها على شكل كسور). وعلى الرغم من عدم وجود قيود مثبتة على رتبة المنحنى - حتى الآن تعتبر أعلى 28 درجة هي أعلى رتبة - تتوقع فرضية غولدفيلد أن نصف المنحنيات البيضاوية في المتوسط ​​لها رتبة 0 ، والنصف الآخر لديهم 1.

قد لا يبدو واضحًا لك كيف يمكن أن توجد منحنيات بيضاوية برتبة أكثر من 1 إذا كان نصف المنحنيات البيضاوية لها رتبة 0 والنصف الآخر لديه 1. إذا كان لديك مربع من كرات كرة الطاولة ، وإذا كنت تعرف أن نصف بالضبط هم أسود ، ونصفهم أبيض ، فلا يمكن أن يكون أحمر.

والأمر الأكثر إرباكًا هو حقيقة أن المنحنيات الناقصية ذات الرتبة 2 أو أعلى ليست موجودة فقط على عدد قليل ، ولكن على عدد لا نهائي. النتيجة السخيفة على ما يبدو هي نتيجة إحصائيات ماكرة تعمل مع اللانهاية. على الرغم من وجود الكثير من المنحنيات من الرتبة 2 وما فوقها ، فهناك العديد من المنحنيات ذات الرتب 0 و 1 بحيث لا تكون المنحنيات ذات الرتب 2 وما فوق ذات دلالة إحصائية. إذا وضعت جميع المنحنيات في صندوق وأخرجتها من هناك بشكل عشوائي ، فإن فرص سحب منحنى برتبة أكثر من 1 تساوي رسميًا الصفر.

ماذا يعني أن رتبة المنحنى هي 0؟ مثل هذه المنحنيات لديها عدد محدود من النقاط العقلانية - وليس أكثر من 16 ، كما أثبت باري مازور في السبعينيات.


دوريان غولدفيلد

هناك أسباب للاعتقاد بأن عددًا كبيرًا جدًا من المنحنيات البيضاوية سيكون لها رتبة 0. إذا كنت تتخيل كيف يعمل المنحنى على طول المستوى ، فسيتبين أن معظم النقاط التي يمر من خلالها لن تكون منطقية. لا يمكن التعبير عن هذه النقاط على أنها كسور ، حتى لو كانت معقدة بشكل تعسفي. إن فرص تقاطع منحنى عشوائي مع العديد من النقاط المنطقية - مجموعة لانهائية - ضئيلة.

قال سميث: "إنني أعتبر الأمر بهذه الطريقة: إذا كنت تأخذ منحنى إهليلجيًا عشوائيًا ، فسيكون لديك أسباب للحصول على رتبة 0. ولا تريد أن يكون لها نقاط منطقية".

يتم تفسير انتشار منحنيات الرتبة 1 بطريقة مماثلة. تحتوي منحنيات الرتبة 1 على العديد من النقاط العقلانية بشكل لا نهائي ، ولكن جميعها محاذاة بدقة شديدة ، بحيث يمكنك ربطها ببعضها البعض في عملية بسيطة إلى حد ما.

بالنسبة لمنحنيات الرتبة 2 وما فوق ، تكون مجموعات النقاط العقلانية أكثر تعقيدًا. تحتوي على عدة مجموعات فرعية لا حصر لها من النقاط العقلانية غير المرتبطة ببعضها البعض.

ما هي فرص ظهور نقطتين مستقلتين؟ - قال غولدفيلد. "منخفض جدًا". تقول فرضيتي أنه يجب أن يحدث هذا نادرًا ".

عندما طرح غولدفيلد فرضيته لأول مرة ، اعتبرها معظم علماء الرياضيات أنها غير صحيحة. وأشاروا إلى نتائج التجارب الحسابية ، والتي اتبعت منها أن المنحنيات برتبة 2 أو أعلى تحدث في كثير من الأحيان أكثر من 0 ٪ من الحالات.

رد غولدفيلد أنهم ببساطة يأخذون النطاق صغيرًا جدًا. وأشار إلى أنه إذا درست أول 10 أعداد صحيحة فقط ، يمكنك الحصول على تقدير غير دقيق للغاية أن 40٪ من الأعداد هي أرقام أولية. وبالمثل ، استقرت هذه التجارب الحسابية من مجموعات فرعية صغيرة من المنحنيات الإهليلجية إلى مجموعات كبيرة من المنحنيات.

"قلت انظروا الأعداد الأولية! كان هذا جوابي. قال غولدفيلد: "نحن بحاجة إلى الصعود أعلى بكثير ، لأنه في البداية يمكن أن يظهر الكثير من المرح".

لا تنطبق فرضية Goldfeld على جميع المنحنيات البيضاوية. يصف عائلة خاصة من المنحنيات البيضاوية ، والتقلبات التربيعية. مثال: منحنى إهليلجي cy ² = x ³ - x ، حيث c ثابت. من خلال تغيير قيمة c ، فإنك تنحني منحنى بيضاوي الشكل. تشير فرضية Goldfeld إلى مجموعة متنوعة لا حصر لها من المنحنيات التي يمكن الحصول عليها عن طريق تغيير قيمة c.

شهد ألكسندر سميث أن غولدفيلد كان على حق. في ورقة جديدة ، يثبت أن 100 ٪ من المنحنيات الإهليلجية (من نوع خاص) لها رتبة 0 أو 1. كما أثبت أن هذه المنحنيات مقسمة بالتساوي بين الرتبين ، على الرغم من وجود الصيد. ويستند برهانه على قسم 50-50 على صحة فرضية بيرش - سوينرتون داير (BJD). تعتبر فرضية BSD واحدة من أشهر المشكلات المفتوحة في الرياضيات. لم يقترب علماء الرياضيات بعد من برهانها ، لكنهم يعتبرونها على العموم صحيحة.

حتى مع هذا التحذير ، تعتبر نتيجة سميث مهمة. يقول علماء الرياضيات أنه يظهر طريقة لإثبات فرضية Goldfeld بشكل كامل دون العبث بفرضية BSD المحبطة. تعطي هذه الطريقة فهمًا جديدًا لطبيعة المنحنيات البيضاوية.

قالت ميلاني وود ، أستاذة الرياضيات في جامعة ويسكونسن: "إن عمل أليكس سميث مثير للاهتمام للغاية ، وأعتقد أنه لا يزال يتعين دراسته ودفع ثمنه". "حقيقة أنه يمكن إثبات ذلك أمر مهم للغاية وثوري."