مقدمة
ما هو هذا النص
إذا سمع الشخص عن "محاكاة للواقع" ، فعلى الأرجح أنه سيخرج بمختلف أعمال الخيال العلمي (مثل Matrix أو The Dark City أو Zero Theorems) أو ألعاب الكمبيوتر. في حالة الأشخاص الذين تكون رؤوسهم مسدودة بدرجة هندسية ، قد تظهر حزم مثل
KOMPAS-3D AutoCAD أو Solid Edge أو NX. من المحتمل أن يتذكر الشخص الذي يستمع إلى العلم أي
نماذج لمختلف بدائل الفضاء .
ولكن هناك مستوى آخر من الواقع ، والذي سيتحول إلى نسيان غير مستحق: المستوى الذي تحدث فيه كل الكيمياء هو مستوى الذرات والجزيئات. يمكن أيضًا محاكاة ذلك بنجاح كبير على جهاز كمبيوتر. نظرًا لأن ميكانيكا الكم مسؤولة عن كل شيء في هذا القسم من الواقع ، غالبًا ما تسمى هذه الحسابات كيمياء الكم. وسنتحدث عن علاقته بالواقع الذي تم دراسته بالطرق التجريبية.
سيتناول هذا النص أهم الأشياء الأساسية. لكن ممارسة قراءة المجلات العلمية والاستماع إلى تقارير مختلفة تظهر أنه يجب تذكيرها باستمرار.
تم تصميم النص للأشخاص الذين يفهمون و / أو يهتمون بكيفية حياة الذرات والجزيئات.مأخوذة من xkcd.comخلفية موجزةحدث ذلك أن زميلًا ، للأسف ، عمل في العلوم الروسية ، دعاني لإلقاء محاضرة في دورته الخاصة لشخصين في واحدة من الجامعات الفيزيائية المعروفة في روسيا. ولكن ، بمصادفة غريبة ، تم نقلها إلى مؤتمر طلابي عقد بالتوازي ... هناك لم تثر اهتمامًا كبيرًا بين الطلاب ، وكنت آسفًا جدًا للمواد ، لذلك قررت أن أزعج هبر قليلاً ، محاولاً تحويل المحاضرة التعليمية إلى مقالة علمية شعبية.
الطرق الفيزيائية لدراسة حياة الجزيئات
نعرف من دورات الكيمياء والفيزياء المدرسية أن جميع المواد تتكون من ذرات أو جزيئات أو أيونات أو توليفات منها. ويبدو أننا نعرف حتى نوع الحياة التي يعيشونها. ولكن يجب أن يكون لهذه المعلومات مصادر موثوقة خاصة بها (طرق البحث) ، وهي كذلك حقًا.
هناك طرق عديدة للتجسس على حياة الذرات. أولئك الذين يرغبون ، على سبيل المثال ، يمكنهم التعرف على بعضهم بمزيد من التفصيل في الكتب المدرسية الكلاسيكية
- Pentin Yu.A.، Vilkov L.V. طرق البحث الفيزيائي في الكيمياء. - م: مير ، 2006 ،
- دراجو ر. الطرق الفيزيائية في الكيمياء. - م: مير ، 1981.
ولكن ، تقريبًا وبسهولة إلى حد ما ، تبرز 3 مجموعات رئيسية من الأساليب:
- طرق التحليل الطيفي
- طرق الحيود
- طرق مختلفة من الفحص المجهري (لا يهم ، نصف شفاف أو مسح ، بالنسبة لنا هذا ليس ضروريًا الآن).
لن يكون هناك حديث عن الأخير ، لكن أدواته لا تقل أهمية عن الأولين.
لماذا لن يكون هناك حديث عن الفحص المجهري(أنا لا أخجل من الكلمة على الإطلاق في الفحص المجهري)
طرق التحليل الطيفي لدراسة المادة
تزودنا هذه المجموعة القوية من الأساليب بأشياء كثيرة جدًا: من البحث عن الجزيئات وتحديدها في الوسط النجمي وعلى الكواكب الأخرى إلى الفحص العادي للمتفجرات في المطار.
المبدأ العام للطرق الطيفية
عند الحديث عن التحليل الطيفي ، عادةً ما يشير إلى مبدأ التشغيل العام التالي.
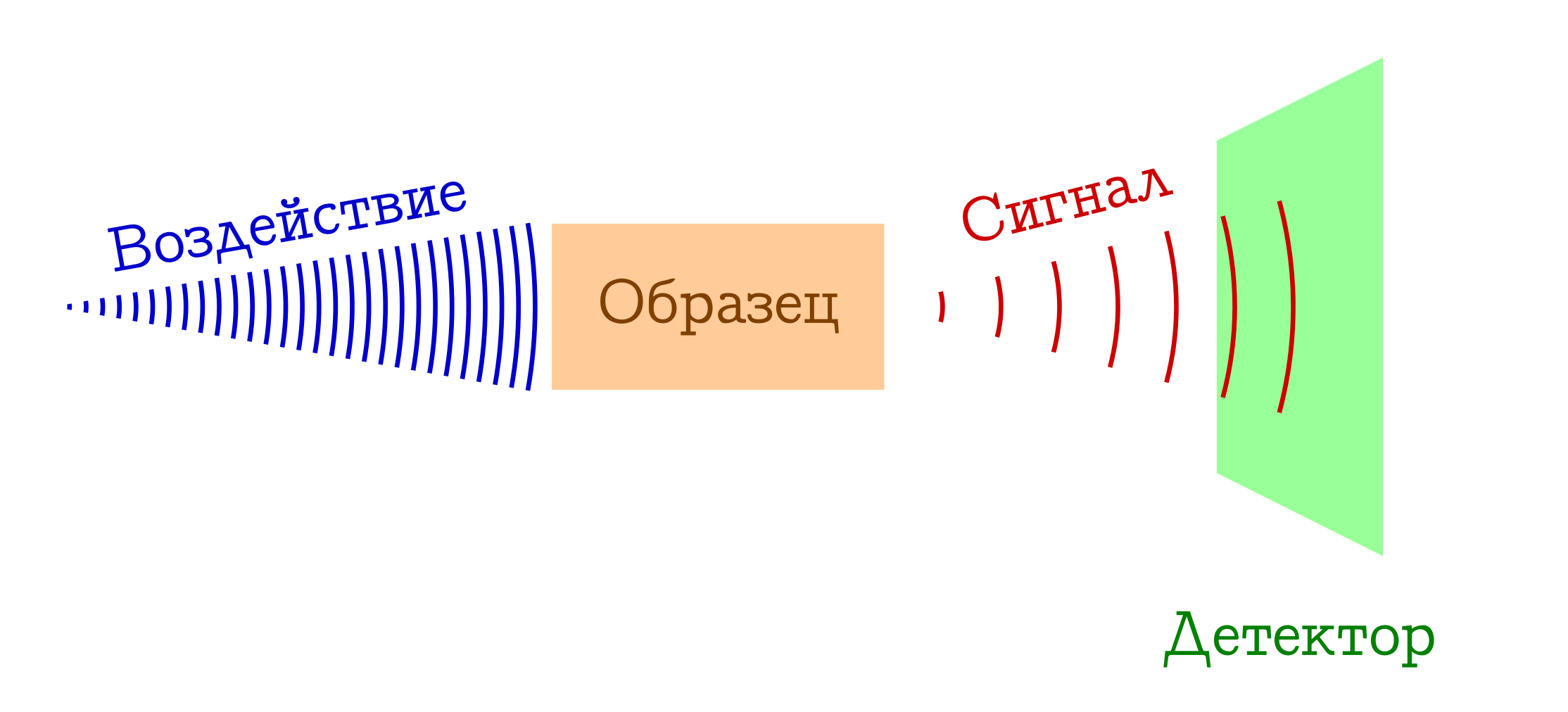
المخطط العام للطرق الطيفية لدراسة المواد
- لدينا شيء نتعامل معه (على سبيل المثال ، مصباح / ليزر / ضوء الشمس) وفقًا للعينة التي تهمنا. غالبًا ما تكون هذه دراسة كهرومغناطيسية ، ولكن يمكن أن تكون إلكترونات (على سبيل المثال ، في التحليل الطيفي الشامل مع التأين عن طريق تأثير الإلكترون) أو مزيج من كل شيء ممكن ومستحيل من البلازما (على سبيل المثال ، في مطياف اللهب ، المحبوب جدًا من قبل طلاب المدارس والطلاب الصغار من أعضاء هيئة التدريس الكيميائية). بطريقة أو بأخرى ، يجب أن يعمل شيء على عينتنا.
- عندما يتعرض لعينة ، يحدث شيء يغير حالته. يمكن أن يكون هذا الانتقال إلى نوع ما من مستوى متحمس (في أي قياس طيفي أو مطياف رامان) ، أو حتى انهيار النظام الجزيئي (كما هو الحال في أطياف الكتلة أو التحليل الطيفي الإلكتروني ). ولكن بطريقة ما يجب أن يكون النمط في مرحلة ما مختلفًا.
- ؟؟؟
- الربح !!! نسجل إشارة معينة (منبعثة أو ممتصة) مع هذا التغيير في العينة على المستوى الجزيئي. يمكن أن يفقد هذا الفوتونات التي تنفق على تغيير العينة (ثم يكون لدينا مطياف الامتصاص) ، أو العكس بالعكس ، الفوتونات الزائدة المنبعثة بعد الإثارة الأولية للمادة (مطياف الانبعاث) ، تغير في الطول الموجي للفوتونات الأولية نتيجة للتفاعل مع المادة (مطيافية رامان ، والمزيد المعروفة في الخارج باسم
Ramenovskaya Ramanova ) ، أو شظايا غبية من الجزيئات الأصلية (كما هو الحال في أطياف الكتلة أو التحليل الطيفي الإلكتروني ). هناك العديد من الخيارات - الجوهر هو نفسه: هناك إشارة!
مثال على هذه الطرق هو مجموعة من الأحرف المختلفة: NMR ، ESR ، MW ، THz ، IR ، UV / Vis ، XRF ، MS ، PES ، EXAFS ، XANES ، إلخ. الخ
كلهم (أو كثير منهم) مألوفين (أو يجب أن يكونوا على دراية) بكل كيميائي. كل هذه الأساليب هي الترسانة المعيارية (غير المكتملة) للباحث الذي يحترم نفسه ويتعامل مع المواد.
النطاقات الطيفية وعلاقتها بحياة الجزيئات
 مأخوذة من xkcd.com
مأخوذة من xkcd.comنظرًا لأنه في الغالبية العظمى من الحالات ، لا يزال التحليل الطيفي مرتبطًا بالإشعاع الكهرومغناطيسي ، فمن المنطقي ربط نطاقات الطيف الكهرومغناطيسي بمختلف جوانب الحياة الجزيئية الذرية. بعد كل شيء ، فإن تردد الموجات الكهرومغناطيسية المستخدمة في التحليل الطيفي هو نوع من "الساعة" التي تسمح لك باكتشاف مدة استمرار هذه العملية أو تلك في الأنظمة الجزيئية. لذا ، بتغيير هذا التردد ، يمكنك الدراسة (وحتى العمل) على العمليات الجزيئية المختلفة.
لذا
- من وجهة النظر الكيميائية ، لا يحدث شيء مثير للاهتمام في نطاق الطول الموجي الطويل للغاية ، لذلك لا يمكنك تذكره.
- مع تردد الراديو والموجات الدقيقة (وحتى الأشعة تحت الحمراء طويلة الموجة ، IR = IR) ، تدور جزيئات مختلفة في مرحلة الغاز: كبيرة وثقيلة - في منطقة الموجات الراديوية (الترددات المنخفضة) ، والصغيرة والخفيفة - في IR (ترددات أعلى).
- في IR ، تحدث اهتزازات جزيئية مختلفة (بشكل رئيسي): جميع الحركات المطابقة وغيرها من الحركات غير الواضحة داخل الجزيئات تكون في IR ذات الطول الموجي الطويل ، وتحدث الاهتزازات الممتدة (التمدد - تقصير أطوال الروابط الكيميائية) في الطول الموجي القصير (حتى 4000 سم -1 ).
- حسنًا ، يأتي مكان الطيف ، حيث تعيش التحولات الإلكترونية المختلفة (حتى منطقة γ-Quanta). عند الترددات المنخفضة (مرئية ، الأشعة فوق البنفسجية = الأشعة فوق البنفسجية والأشعة السينية الناعمة) ، تعيش التحولات المرتبطة بإلكترونات التكافؤ بشكل أساسي.
لماذا نرى؟بالمناسبة ، بالتحديد بسبب التحولات الإلكترونية التي يمكننا رؤيتها: في أعيننا (في المخاريط) هناك هياكل لها
شبكية في تكوينها. عندما يمتص هذا الجزيء الفوتون المرئي ، تنكسر فيه رابطة مزدوجة ، مما يؤدي إلى أزمرة cis-trans. وهذا التغيير هو ما نعتبره الإشارة الأساسية ، التي تنتقل بعد ذلك إلى دماغنا.
ولكن مع زيادة طاقة الفوتون (أي بتواتر متزايد ، كما نتذكر من صيغة بلانك E = ح ن ش ) نصل إلى طبقات أعمق وأعمق من البنية الإلكترونية ، حتى نرتاح في نطاق الأشعة السينية إلى قذائف 1s النهائية ( أو ، كما يطلق عليها X-ray ، K ).
لذا ، باختيار الطول الموجي المناسب للإشعاع الكهرومغناطيسي ، يمكننا أن ننظر بمزيد من التفصيل في عملية معينة في الجزيئات.
طرق حيود المواد
الآن دعونا نتحدث قليلاً عن الحيود. الرسم التخطيطي لمثل هذه التجارب بسيط أيضًا.
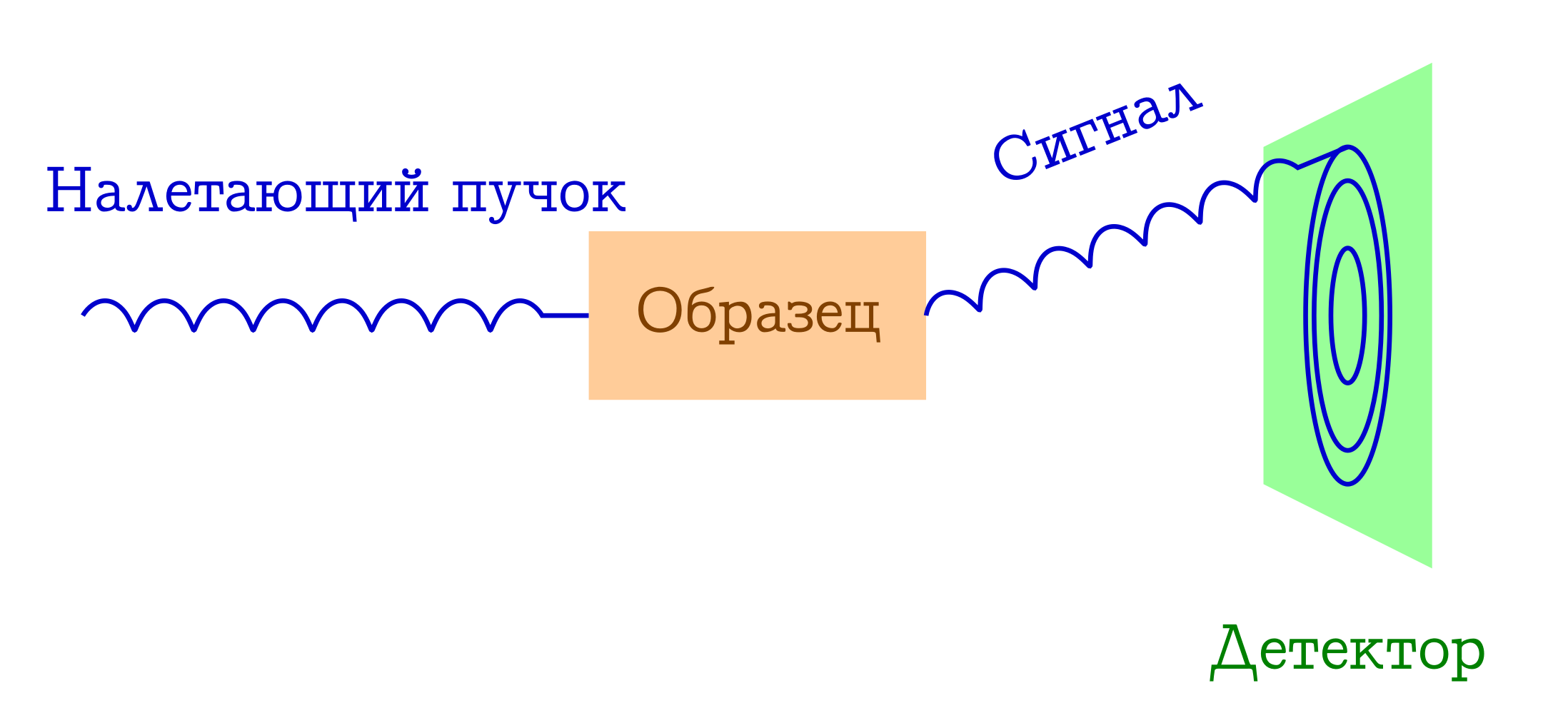
مخطط عام لطرق الحيود لدراسة المواد
- شعاع من بعض الجسيمات يطير على العينة. غالبًا ما تكون إما فوتونات الأشعة السينية ، أو الإلكترونات ، أو النيوترونات.
- تنتشر هذه الجسيمات بواسطة آليات مختلفة بشكل مرن على الذرات في العينة التي تهمنا (أي ، دون تغيير طول الموجة وطور الموجة ، فإنها ببساطة تغير اتجاه رحلتها). لا يحدث أي شيء للعينة من هذه الجسيمات الواردة: فهي ببساطة ليس لديها وقت للتفاعل معها.
- تعمل المسافات بين الذرات بمثابة صريف حيود لحزمة السقوط ، وبالتالي ، سنرى صورة حيود جميلة على الكاشف.
من الفقرة الأخيرة ، تنشأ حالة الطول الموجي للجسيمات الساقطة (λ): يجب أن تكون من نفس الترتيب أو أقل من الترتيب المميز للمسافات بين الذرات ، لذا فإن typical النموذجي لهذه الطرق هو 1 - 0.01 Å.
الأنواع الرئيسية للأخطاء عند مقارنة التجارب والحسابات النظرية
ونتيجة لذلك ، لدينا صورة مثيرة للاهتمام للغاية: في التحليل الطيفي وفي الحيود ، نلاحظ نوعًا من الإشارة اليسرى ، والتي تشير بطريقة ما
بشكل غير مباشر إلى ما يحدث بالفعل في النظام الجزيئي.
القياس مع الكهف الأفلاطونيتذكر هذه اللوحة بشكل خرافي
أسطورة كهف أفلاطون . لدينا عالم حقيقي معين من الجزيئات. لكننا نرى فقط الظلال منه على جدار الكهف (الكاشف) ، وهي عرض غير مكتمل لجميع الأشياء المثيرة للاهتمام التي تحدث على هذا المستوى من الواقع.
ولكن ، لحسن الحظ ، في بعض الأحيان يمكننا حسابًا نظريًا للإشارة التي تهمنا (على سبيل المثال ، في التحليل الطيفي بالميكروويف أو الأشعة تحت الحمراء أو الأشعة فوق البنفسجية / Vis) ، وأحيانًا يمكننا استخراج الكميات ذات الأهمية المتوفرة من الإشارة المرصودة للحساب الكيميائي الكمي (على سبيل المثال ، المسافة بين الذرات في الجزيء ، عزم ثنائي القطب ، وما إلى ذلك). وهنا لدينا فرصة أن تتحد التجربة العددية والحقيقية في المرحلة الشغوفة من المقارنة مع بعضها البعض ... وهنا يمكن أن تحدث أربعة أنواع من الأخطاء كمعيار.
انتباه! لا يعني مصطلح "خطأ" هنا أن نتيجة المقارنة خاطئة بشكل واضح. إنها مجرد أن أساس المقارنة يصبح مهتزًا ومستنقعيًا للغاية ، ويمكن لخطوة قذرة واحدة أن تفسد العمل بأكمله بسهولة.
- الظروف المختلفة للتجربة و / أو الحساب (حالة التجميع ، درجة الحرارة ، الضغط ، إلخ). يمكننا فجأة البدء في مقارنة أنظمة مختلفة فيما بينها ، لسبب ما نعتبرها متشابهة. على سبيل المثال ، من الواضح أن إضافة ملعقة أو خمس ملاعق صغيرة من السكر إلى فنجان شاي سيؤدي إلى نفس النظام المادي المسمى "الشاي مع السكر" ، لكن خصائص هذا النظام ستكون مختلفة تمامًا. ويمكن قياسه بسهولة. على سبيل المثال ، باستخدام مقياس حرارة (قياس درجة حرارة الشاي بعد إذابة السكر مباشرة) أو مع اللسان (إحدى طرق التحليل الحسية). لذلك عند مقارنة الأنظمة الناتجة مع بعضها البعض (سواء أكان كوبًا حقيقيًا من السكر مع الشاي أو طراز الكمبيوتر الخاص به) ، يجب ألا ننسى أن أوجه التشابه لها حدودها ، وأنه إذا قللنا من هامش الخطأ لـ "التشابه" ، فسوف نجد الاختلافات في النهاية.
- اختلاف المعنى المادي و / أو الرياضي للمعلمات (قد لا توجد معلمة المعنى المادي بالمعنى المعتاد). هنا أيضًا ، كل شيء بسيط: إذا قارنا كميتين باسم مشابه ، فهذا لا يعني أن الكميات لها نفس المعنى المادي. على سبيل المثال ، تصنيف نائب بين جميع سكان المدينة مقابل تصنيف فقط بين الجدات. كل من هذا التصنيف وهذا (أيًا كان) ، يمكن أن ترتبط هذه الأرقام (أو أيًا كانت) ارتباطًا وثيقًا ببعضها البعض ، ولكن لا يزال معنى هذه المعلمات مختلفًا ، ويمكن اكتشاف هذا الاختلاف.
- أخطاء "عشوائية" . يتضمن هذا بعض الأخطاء المنهجية التي لا يدركها المجرب / المحاكي ، أو الأخطاء العشوائية في التجربة / الحساب التي لا يمكن التحكم فيها و / أو التنبؤ بها. من حيث المبدأ ، يمكن أن تصبح هذه الأشياء نفسها موضوعًا للتحقيق في مختلف التأثيرات المنهجية المثيرة للاهتمام.
أو مجرد تقدير لنسبة S / N ("الإشارة إلى الضوضاء") الأكثر فائدة. - والخطأ القياسي الأخير هو نمو أيدي المجرب / الآلة الحاسبة من عظم الحوض ، أي الأخطاء البشرية العادية. ليست هناك حاجة للتحقيق في أي شيء ، فقط تحقق مرة أخرى من العمل أو كرر التجربة للعثور على الدعامة المقابلة وإزالتها.
لا يمكن قول شيء أكثر واقعية عن النوعين الأخيرين من الأخطاء ، ولكن عن النوعين الأولين ، وإذا كنت تستخدم طريقة بحث محددة ، فيمكنك قول الكثير من الأشياء. لذلك ، سنركز عليها. سيكون التركيز الرئيسي في هذه الحالة على الاختلافات الهيكلية للجزيئات.
الخطأ رقم 1. الاختلافات في الخصائص الجزيئية تحت ظروف مختلفة
كلوريد الصوديوم: عندما لا توجد أخطاء
لسبب ما ، لا يخطر على بال أحد أن يقول أن البلورة المفردة من كلوريد الصوديوم (NaCl) ، وهي جزيء ضخم من Na
+ و Cl
- أيونات ، وجزيء NaCl الدياتومي ، الذي يتم الحصول عليه عن طريق تبخر هذه البلورة في درجات حرارة مجنونة ، يكون لها نفس الشيء دعنا نقول الهيكل.
وحتى إذا افترضنا أن المسافات بين الكلور والصوديوم (
r NaCl ) على الأقل هي نفسها هنا وهناك ، فستضعنا التجربة في مكانها:
أين نرتكب خطأفي الواقع ، مع مثل هذه المقارنة ، نسمح بإمكانية الخطأ رقم 2 ، ولكن كل شيء على ما يرام هنا ، إذا قمنا بتقييم أخطاء هذه المقارنة ، فستكون بترتيب 0.01 Å ، وهو أقل بكثير من اختلاف المعلمات المقارنة. أي هذا ليس خطأ ، ولكنه تأثير حقيقي.
كيفية الحصول على المسافة بين كاتيون الصوديوم وأنيون الكلور في بلورة الملح بنفسكإن الحصول على المسافة بين الذرات في جزيء كلوريد الصوديوم من البيانات التجريبية ليس إجراءً معقدًا أيضًا. لكن المشكلة هي فقط أن مثل هذه التجربة شيء معقد. لذلك ، من الأسهل استخدام قاعدة بيانات حيث تم بالفعل تحديد المسافات المطلوبة.
ولكن للحصول على المسافة بين الذرات في البلورة ، يكفي فقط كثافة الملح البلوري للطاولة 2.1 = 2.165 جم / سم
3 ، والتي يمكن
الحصول عليها بسهولة من ويكيبيديا وقياس نفسك في المنزل.
لحساب المسافة التي نحتاجها:
- كثافة بلورة كلوريد الصوديوم ،
- معرفة موقع أيونات هذه البلورة.
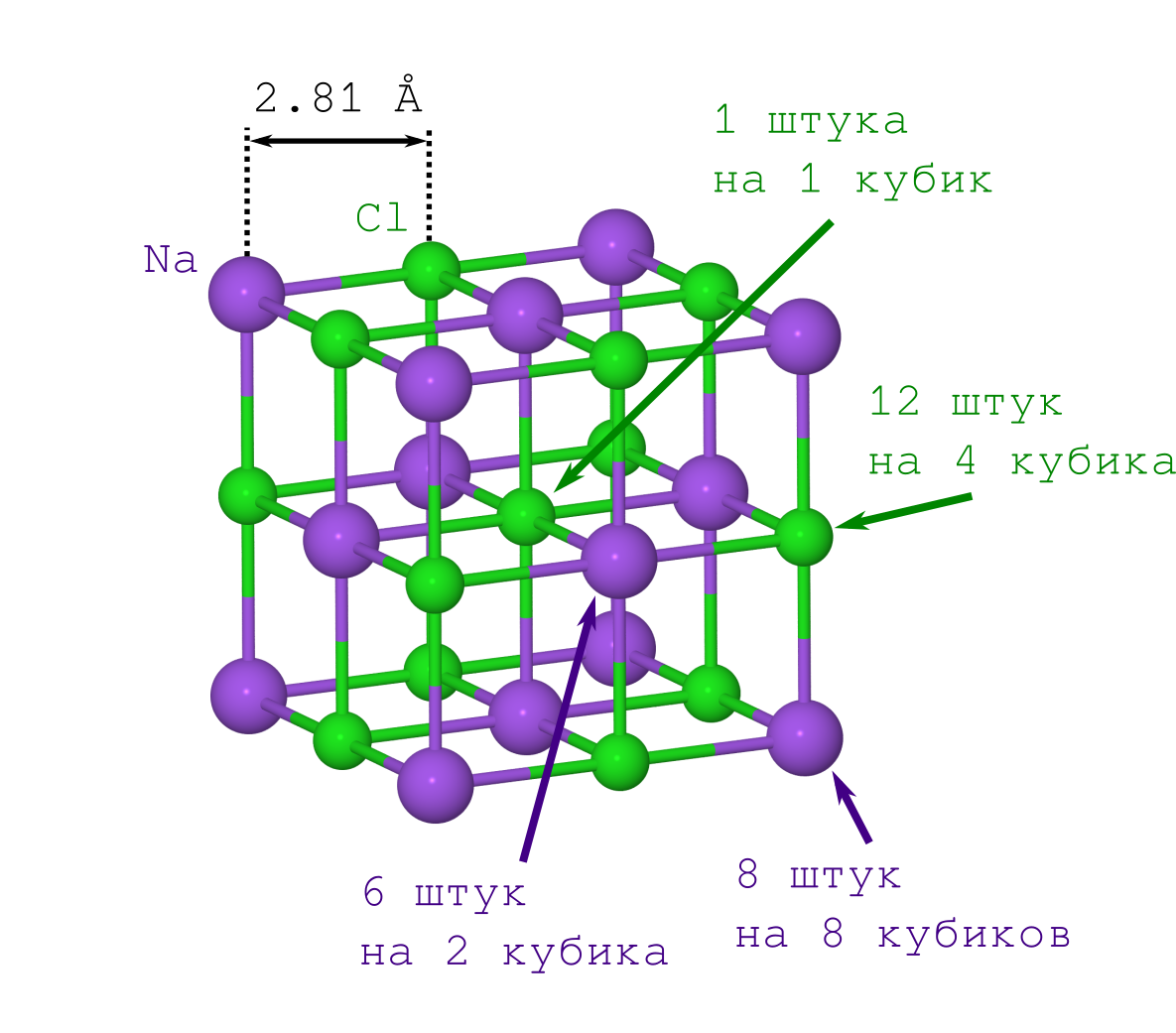
إذا كنت قد فعلت ذلك للمرة الأولى (على سبيل المثال ، في بداية القرن العشرين) ، فسيتعين عليك أن تعذب نفسك بالنقطة الثانية. لكن هذا معروف بالفعل لدى الناس الحديثين: إن شبكة NaCl لها شكل مكعب يتناوب فيه Na
+ و Cl
- ions مع بعضها البعض (انظر الصورة أعلاه). بضرب الجزء المشار إليه من البلورة ("نسخ ولصق" القطعة المحددة وضبطها على التكرار السابق وجها لوجه) ، نحصل على بلورة NaCl بأي حجم مرغوب وأي شكل (ماين كرافت) مرغوب فيه.
لذا يجب أن تكون كثافة هذا المكعب هي نفس كثافة البلورة بأكملها. بالنظر إلى أن الكثافة
rho= fracmV (أي الكتلة لكل حجم) ، اتضح أنه بمعرفة الكتلة والتعبير الهندسي للحجم ، يمكننا حساب المسافة بين الذرات.
حجم المكعب واضح: طول الضلع ضعف المسافة Na - Cl (
L=2r mathrmNaCl ) ، مما يعني أن الحجم المطلوب هو
V=L3=8r mathrmNaCl3 .
الكتلة ليست بهذه البساطة. تقع معظم ذراتنا على رؤوس وحواف ووجوه المكعب ، مما يعني أنها تنتمي في نفس الوقت إلى العديد من هذه المكعبات. يجب أن يؤخذ هذا في الاعتبار في الحسابات.
لنبدأ بأيونات Na
+ . لدينا نوعان فقط منهم (انظر نمط الشبكة البلورية):
- تلك الموجودة في رؤوس المكعب (هناك العديد من رؤوس المكعب ، أي 8 ، وهي في وقت واحد في 8 مكعبات ، لذلك ستحتاج إلى قسمة هذا الرقم على 8) ،
- تلك التي تقع على الوجوه (هناك 6 منهم ، وهم في نفس الوقت ينتمون إلى مكعبين).
نتيجة لذلك ، نحصل على أن يحتوي المكعب الخاص بنا
8 cdot frac18+6 cdot frac12=4 أيون الصوديوم.
الآن حول Cl
- . هناك أيضًا نوعان فقط منهم (انظر نمط الشبكة البلورية):
- تلك التي تقع على حواف المكعب (هناك 12 منها ، وهي مملوكة بشكل مشترك بأربعة مكعبات) ،
- أن Cl - الموجود في وسط المكعب ، هو واحد وينتمي إلى مكعبنا فقط.
لذلك ، يحتوي المكعب لدينا
12 cdot frac14+1 cdot frac11=4 أيون الكلور.
من الواضح أن تكوين البلورة يتوافق مع الصيغة الكيميائية لـ NaCl ، لكن كتلة مكعبنا متساوية (لا تنس أن كتل الذرات في الجدول الدوري معطاة
بوحدات الكتلة الذرية ):
m=4 cdot( underbraceM mathrmNa23 textam+ UnderbraceM mathrmCl35.5 textamu)=234 textamu=234 cdot1.66 cdot10−24 textg=3.88 cdot10−22 textg\.
الآن من العلاقة
rho= fracmV يمكننا عمل معادلة للطول
r mathrmNaCl :
r mathrmNaCl3= left( fracm8 rho right) ،
والتي يمكن حلها بسهولة:
r mathrmNaCl= left( fracm8 rho right)1/3= left( frac3.88 cdot10−22 [ textg]8 cdot2.17 [ textg/ textcm3] right)1/3=2.82 cdot10−8 [ textcm]=2.82 [ textÅ] .
من البيانات المأخوذة من البلورات بالأشعة السينية 2.81 Å (على سبيل المثال ، من
Abrahams، SC؛ Bernstein، JL Accuracy لمقياس حيود تلقائي. قياس عوامل هيكل كلوريد الصوديوم // Acta Crystallographica (1965) 18، 926-932 ) لم
نفتقد سوى 0.01 Å ، وهو بارد بما فيه الكفاية.
قد يعتقد شخص ما أن الفرق 0.45 Å غير ذي أهمية ، ولكن هذا هو تقريبًا نصف قطر بور (0.52 Å) ، وهو ما يعادل أكبر مسافة محتملة للإلكترون ، والمعايير الذرية الفارق كبير.
لماذا يختلف كلوريد الصوديوم في شكل جزيء ذري عن بلورةكل شيء بسيط للغاية هنا. تخلق الشبكة البلورية اللانهائية إمكانية "القفز" الذي لا رجعة فيه لإلكترونات الصوديوم 3s
1 لكل ذرة كلور ، حيث يتم تعويض فرق الشحن الناتج بالتفاعل مع الجيران.
3s
1 ( ), ,
«» :
Na:Cl↔Na+Cl−
() (), .
,
±1 , , .
NaCl (2.36 Å),
d=q⋅rNaCl=9.0 [] اين
q≥0 (
+q ,
−q )
, « » 0.21, ..
d=0.21⋅9.0=1.9 [qe⋅Å] , :
q=drNaCl=1.92.36=0.8 . «» 0.2 NaCl NaCl .
الفيروسين
يجدر الانتقال من البلورات الأيونية إلى البلورات الجزيئية التي يتم فيها تعبئة الجزيئات بكثافة ، بحيث يصبح من الممكن فجأة المقارنة ، ودون أي تحفظات.لكن لا يجب نسيان الفرق. وهناك أيضًا مثال كلاسيكي حول هذا الموضوع: جزيء الفيروسين .هذا هو أبسط اتصال شطيرة. في ذلك ، توجد ذرة حديدية محايدة (مثل قطعة صغيرة) محصورة بين حلقتين أروماتيتين (خمس كعكات).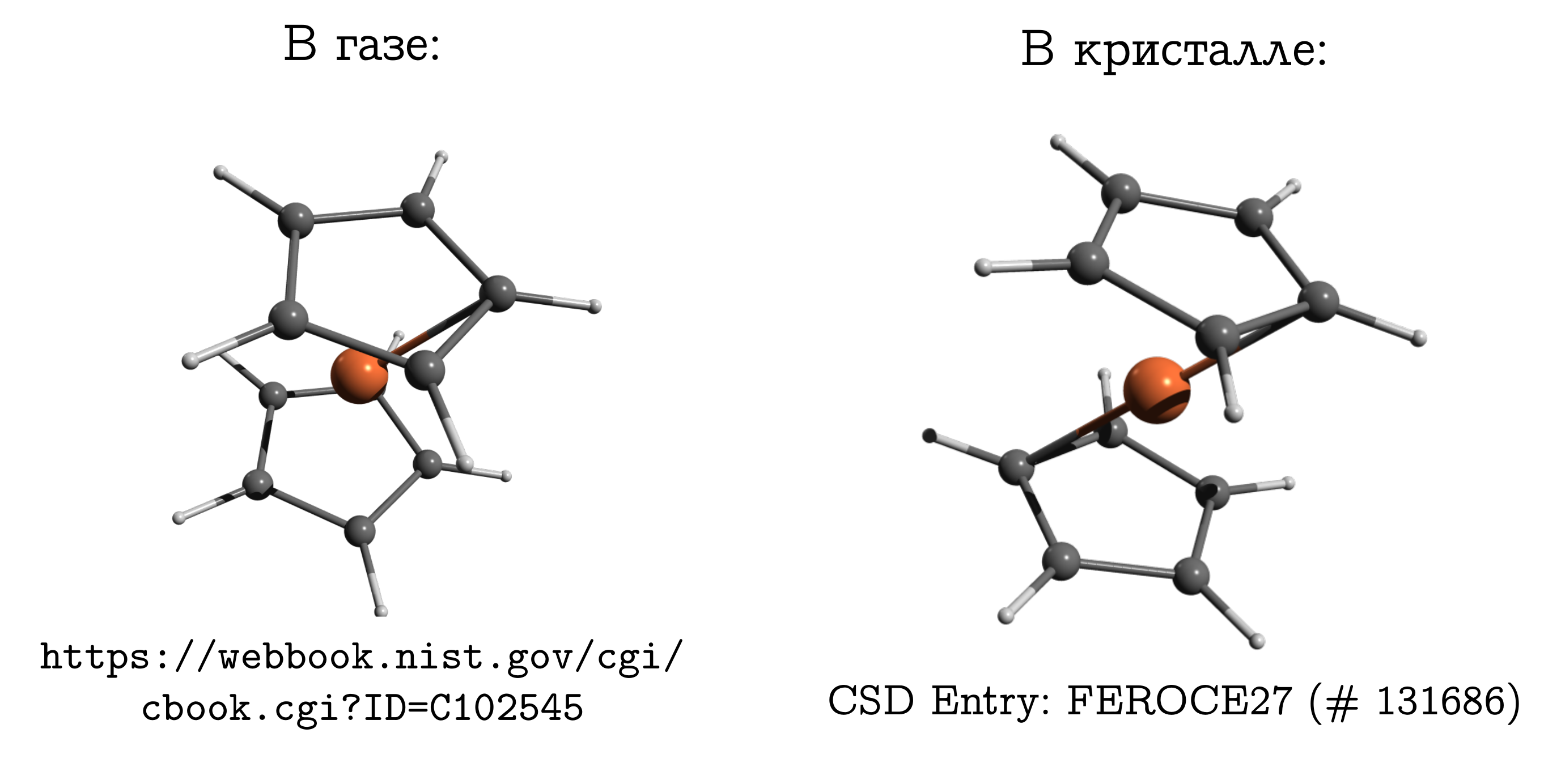 يمكن تبخر هذا الجزيء بسهولة تامة ، واكتشف أن ما يسمى بالهيكل الأكثر استقرارًا في مرحلة الغاز هو التشكل المعوق. في ذلك ، فإن ذرات الكربون والهيدروجين للحلقات العلوية والسفلية متقابلة (انظر الصورة أعلاه) ، حيث تكون تفاعلات التشتت في هذه الحالة أقوى بين هذه الأجزاء من الجزيء ، والتشتت مفيد دائمًا.إذا أخذنا بلورة الفيروسين ، فعندئذٍ يتبين أن الجزيئات الموجودة بها لها تشكيل ثابت مختلف (يُسمى مثبط للهيدروكربونات) ، حيث يكون الهيدروجين والكربون في إحدى الحلقات أعلى / تحت رابطة C - C الخاصة بالأخرى. هناك تفاعلات تشتت بين الجزيئات ، وينشأ تشابه ، يبدو غير مريح لبنية الجزيء من حقيقة أنه من الأسهل للجزيئات أن تتناسب معًا فقط في شكل غير مريح ، ويتم تعويض هذا الإزعاج الشخصي من خلال التفاعل مع بعضها البعض.
يمكن تبخر هذا الجزيء بسهولة تامة ، واكتشف أن ما يسمى بالهيكل الأكثر استقرارًا في مرحلة الغاز هو التشكل المعوق. في ذلك ، فإن ذرات الكربون والهيدروجين للحلقات العلوية والسفلية متقابلة (انظر الصورة أعلاه) ، حيث تكون تفاعلات التشتت في هذه الحالة أقوى بين هذه الأجزاء من الجزيء ، والتشتت مفيد دائمًا.إذا أخذنا بلورة الفيروسين ، فعندئذٍ يتبين أن الجزيئات الموجودة بها لها تشكيل ثابت مختلف (يُسمى مثبط للهيدروكربونات) ، حيث يكون الهيدروجين والكربون في إحدى الحلقات أعلى / تحت رابطة C - C الخاصة بالأخرى. هناك تفاعلات تشتت بين الجزيئات ، وينشأ تشابه ، يبدو غير مريح لبنية الجزيء من حقيقة أنه من الأسهل للجزيئات أن تتناسب معًا فقط في شكل غير مريح ، ويتم تعويض هذا الإزعاج الشخصي من خلال التفاعل مع بعضها البعض.لماذا يختلف الفيروسين عن الإيثانعادة ما يتعين على الشخص الملم بالكيمياء أن يتغلب على نفسه ليتذكر بنية الفيروسين في الغاز. بعد كل شيء ، لديه ذكريات من الإيثان (C
2 H
6 ) ، حيث يتم تثبيط التشكل الأكثر استقرارًا (عندما تقع هيدروجين قطعة واحدة من CH
3 "بين" هيدروجين CH
3 آخر) ، لأن في هذا الموقف ، يتم تقليل التنافر بين الذرات بين قذائف الإلكترونات للهيدروجين.

مقتبس من
www.chem.msu.su/rus/teaching/stereoوهنا الاختلاف كله في المسافة. الشكل القياسي لإمكانات تفاعلات التشتت هو إمكانات لينارد جونز (هذا ، بالمناسبة ، واحد ، وليس رجلين):
V mathrmLJ(r)= fracAr12− fracBr6
في ذلك ، يتم أخذ المصطلح الأول من التنافر بين الذرات ، والثاني من الجذب بين الذري الناشئ عن تقلبات كثافة الإلكترونات. بشكل عام ، تبدو هذه الإمكانية شيئًا مثل هذا:
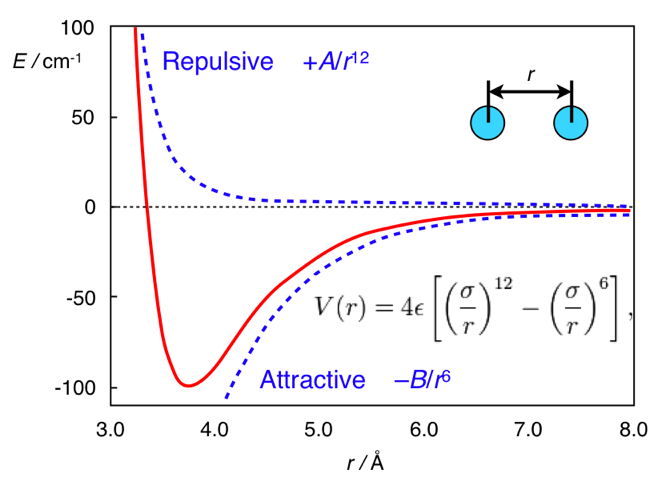
إمكانات لينارد جونز. مقتبس من
chemistry.stackexchange.com/questions/34214/physical-significance-of-double-well-potential-in-quantum-bondingوفي حالة الإيثان ، تكون ذرات الهيدروجين قريبة جدًا من بعضها البعض ، لذا فهي (بالنسبة إلى الحد الأدنى) على الجانب الأيسر من المنحنى ، وتتميز بالتنافر. في حالة الفيروسين ، توجد بين الحلقات طبقة ذات حجم غير مريض (ذرة حديدية) ، حيث تكون الحلقات بعيدة بما يكفي حتى لا تشعر بالتنافر بين الذرات. ولذا فهم على الجانب الصحيح (الجذاب) من الإمكانات.
الهيستامين
في حالة الفيروسين رأينا ما يسمى الاختلافات في المطابقة: ظل الجزيء كما هو (أي لم يتم كسر أو تكوين روابط كيميائية) ، وتغير شكله قليلاً.
ولكن يمكن أن تكون الاختلافات أقوى ، على سبيل المثال ، إذا كان ما يسمى ب
التحولات الصنعية . Tautomerization هو فئة من التفاعلات الكيميائية التي تحدث بسهولة وبسرعة بحيث أنه نتيجة لذلك ، يمكن أن يكون لدينا في نفس الوقت العديد من أيزومرات جزيء واحد ، تمر بسهولة إلى بعضها البعض. تسمى هذه الأيزومرات tautomers.
مثال قياسي على ذلك: الحشو كيتو-إنول في الكيتونات:

في معظم الأحيان ، كما هو الحال في هذا المثال ، ترتبط الحشو بنقل البروتون من مكان دافئ إلى آخر. وترتبط هذه التفاعلات
بتأثير النفق ، حيث يكون الهيدروجين ، باعتباره أخف الذرات ، أكثر عرضة.
تتميز هذه التحولات الكيميائية بالعديد من الجزيئات البيولوجية ، على سبيل المثال ،
القواعد النيتروجينية التي يتكون منها DNA أو
السكريات .
ولكن عند الانتقال من نظام إلى نظام ، غالبًا ما تتغير ثوابت التوازن لمثل هذه التفاعلات ، لذلك في مراحل مختلفة يمكننا ملاحظة تراكيب صنعية مختلفة.
مثال على ذلك هو جزيء الهيستامين (انظر الشكل أدناه).
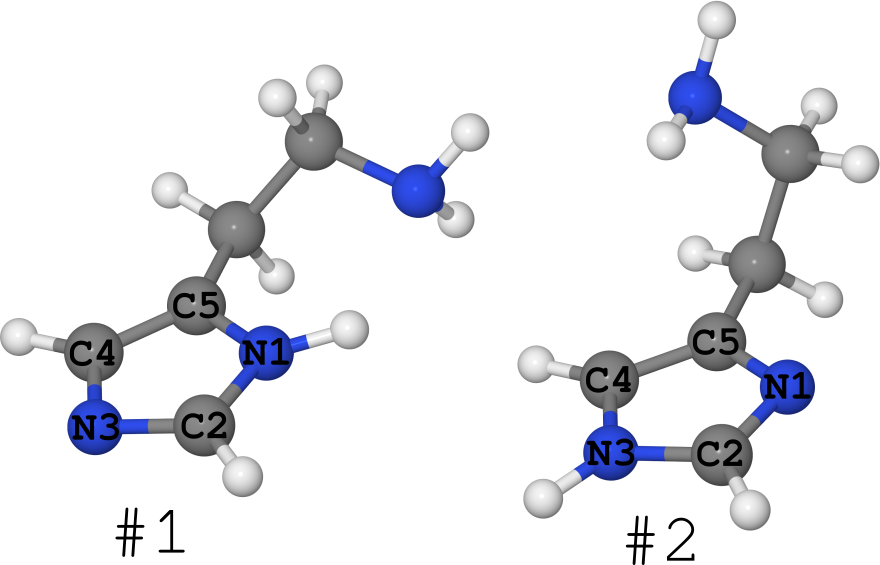
إنه موجود على شكل اثنين من الصائغ (أنا صامت بشكل عام حول عدد المطابقين ، هناك الكثير منهم):
- # 1 ، حيث يجلس الهيدروجين على النيتروجين N1 ،
- # 2 ، حيث يجلس الهيدروجين على النيتروجين N3.
وقد حدث أن لهذا الجزيء هياكله في مراحل مختلفة معروفة.
- في البلورة ، يتم تجميدها تمامًا في شكل رقم 1. (انظر مقالة DOI: 10.1021 / ja00796a011 والهيكل الموجود في بنك هياكل كامبريدج تحت اسم "HISTAN" و / أو الرقم 1176642)
- في المحاليل المائية ، يوجد هذا الجزيء في كلا الشكلين ، و tautomer # 2 أكبر بشكل ملحوظ ( DOI: 10.1021 / ja027103x ).
- في الغاز ، يوجد الهيستامين بالتساوي في الشكل رقم 1 وفي الشكل رقم 2 ( DOI: 10.1021 / ja980560m ).
أي تحتوي الأطوار المختلفة على أعداد مختلفة من الجزيئات المختلفة ، مما يعني أنها أنظمة مختلفة.
استنتاج الخطأ # 1

الاستنتاج الرئيسي المستخلص من الأمثلة المذكورة أعلاه هو كما يلي:
عند مقارنة الحسابات في مرحلة واحدة وتجربة في مرحلة أخرى ، يجب أن يتم إعدادها للاختلافات المنهجية.
هذا لا يعني أنه ليس من الضروري المقارنة: من الضروري المقارنة ، ولكن من الضروري فقط أن تكون أكثر انتقادًا للاختلافات و / أو المصادفات الموجودة ، وتقييم هذه التأثيرات إن أمكن.
الخطأ رقم 2. المعلمات الجزيئية "حديقة الحيوان".
يتم وصف الخطأ الثاني بإيجاز على النحو التالي: إذا تم استدعاء المعلمات بشكل مشابه ، ولكن ليس متطابقًا ، فهذه معلمات مختلفة.
لفهم مصدر هذا الخلاف بين النظرية والتجربة ، يجب على المرء أن يحلل بمزيد من التفصيل كل من الطرق التجريبية القياسية المستخدمة للحصول على المعلمات الجزيئية والنماذج التي تحسب كميات مماثلة من النظرية بحتة.
وهنا سنتحدث مرة أخرى فقط عن الهياكل.
كيفية الحصول على الهياكل الجزيئية التجريبية
من أجل تقييد أنفسنا بطريقة أو بأخرى ، سنتحدث فقط عن طرق لدراسة بنية الجزيئات الفردية ، أي عن مرحلة الغاز.
لدينا مصدران رئيسيان لهذه المعلومات:
- حيود إلكترون الغاز ،
- التحليل الطيفي بالميكروويف.
سوف نتحدث عن كل من هذه الأساليب بمزيد من التفصيل.
حيود إلكترون الغاز
هذه الطريقة قديمة جدًا ، نشأت في الثلاثينيات من القرن العشرين ، عندما أجرى العلماء الألمان مارك وويرل التجارب الأولى على حيود الإلكترونات عن طريق الغاز.
قليل من الناس يعرفون ، لكن طريقة البحث هذه تشارك في تلقي ثلاث جوائز نوبل في الكيمياء.
3 نبلاء بمدخل إلكتروني- حصل بيتر ديبي في عام 1936 على جائزته مع الصياغة:
"[لعمله على] التركيب الجزيئي من خلال تحقيقاته في لحظات ثنائي القطب وحيود الأشعة السينية والإلكترونات في الغازات "
هذا هو الإشارة الصريحة الوحيدة لحيود إلكترون الغاز في مزايا الفائز ، وليس بدون سبب. تسمى معادلة حيود الإلكترون الأساسية لكثافة الانتثار الجزيئي Debye.
في الواقع ، معادلة ديبايIij(s)=gij frac sin(srij)rij
هنا
Iij يشير إلى كثافة التشتت للإلكترونات (أو الأشعة السينية أو الجسيمات الأخرى) بواسطة زوج من الذرات i و
j على مسافة
rij بصرف النظر
s= frac2 pi lambda sin left( frac theta2 right) هل إحداثيات الانتثار مرتبطة بزاوية الانتثار
theta وطول موجة الجسيمات
lambda و
g - قدرة هذا الزوج من الذرات على تشتيت الجسيمات المشتتة.
وعلى الرغم من حقيقة أن أي شيء يتذكره هذا الفيزياء الرائعة ( نموذج الحلول الأيونية ، ونموذجها لحساب السعة الحرارية للبلورات ) ، ولكن ليس حيود الإلكترون ، فقد حصل على الجائزة العلمية الرئيسية (على وجه الخصوص) لذلك.
- لينوس بولينج عام 1954. نعم ، الشخص الذي حصل على جائزتي نوبل شخصيتين ،
بل ووضع العالم بأسره على فيتامين سي ، جريت بولينج. عندما كان يعمل في Kaltekh ، على وجه الخصوص ، كان يعمل في حيود إلكترون الغاز (انظر ، على سبيل المثال ، DOI: 10.1021 / ja01873a047 ). وبالطبع ، ساعدته معرفة الكيمياء الهيكلية للجزيئات الحرة على إنشاء النظرية الشهيرة للترابط الكيميائي (ولكن دعونا لا نقلل من خلفيته البلورية الكبيرة هنا). - أود هاسل ، 1969 حائز على جائزة. حصل على جائزة نوبل 1/2 لاكتشاف التوازن المطابق. وقد فعل ذلك على أساس دراسة حيود الإلكترون للهكسان الحلقي. يوجد هذا الجزيء على شكل شكلين: كرسي (كرسي) وحمام (في التقليد الإنجليزي - قارب ، قارب).

من هنا: www.shapeways.com/product/N5FE298DS/cyclohexane-2-molecules-boat-and-chair-form
تتحول هذه الخيارات لترتيب الذرات بسرعة إلى بعضها البعض ، ولكن في ذلك الوقت لم يعرفوا عنها ، ويعتقدون أنه يجب تحقيق واحد فقط من الهياكل. فقط إشارة حيود الإلكترون لا تريد أن يتم وصفها من قبل أي من هذه الهياكل ، وفقط مزيج من الإشارات من كلا التطابقين يمكن أن يفسر نمط الحيود المرصود (يمكن العثور على المزيد حول هذا في كتاب I. Khargittai "Frank Science. المحادثات مع الكيميائيين المشهورين").
مخطط الطريقة نفسها بسيط للغاية (انظر الصورة أدناه).
يحدث الشيء في فراغ.
- يتم إخراج الإلكترونات السريعة باستمرار من الكاثود ، والتي يتم تسريعها في مجال الأنود إلى طاقات 40-60 كيلو فولت.
- تركز الإلكترونات المنتشرة بما فيه الكفاية (ولكن السريعة) بواسطة عدسة مغناطيسية ، وبعد ذلك تتحول إلى شعاع ضيق.
- يتم تثبيت غرفة بمادة متعامدة مع الشعاع. يتم تسخين العينة حتى الغليان ، ويتلامس البخار الناتج مع شعاع الإلكترون.
- تشتت الجزيئات الإلكترونات بنجاح ، وتطير بعيدًا بهدوء بعيدًا ، حيث تسقط على الفيلم.
- عادة أمام الفيلم وضع ما يسمى ب. جهاز القطاع. هذه شاشة تدور بسرعة كبيرة بشكل غير عادي. والحقيقة هي أن الإلكترون لديه احتمال الانحراف عن اتجاهه الأصلي (بزاوية تشتيت كبيرة theta ) ، يسقط بسرعة كبيرة. لذلك ، من أجل تهدئة هذا الانخفاض في الشدة ، فإن القطاع يطغى بشكل موحد على الجزء المركزي من الفيلم ، ويترك الجزء البعيد مفتوحًا. والنتيجة هي صورة مضاءة بالتساوي.
- يلتقط مصيدة الشعاع تلك الإلكترونات غير المنتشرة على الإطلاق (وهناك الكثير منها).
- حسنًا ، حتى لا تطير الجزيئات في جميع أنحاء الجهاز ، مما يؤدي إلى اتساخها ، يتم تجميدها في مصيدة باردة مبردة بالنيتروجين السائل.
والنتيجة هي نفس نمط الحيود لحلقات متحدة المركز موصوفة بواسطة معادلة ديباي (هذه إشارة). يمكن بعد ذلك سحب المعلمات الجزيئية المختلفة منه مباشرة.
أين يمكنني العثور على مختبرات الغاز الإلكترونية؟لم يبق الكثير.
ولكن يوجد في روسيا اثنان منهم: موسكو (في قسم الكيمياء بجامعة موسكو الحكومية) ، وفي جامعة إيفانوفو الكيميائية التكنولوجية.
التحليل الطيفي بالميكروويف
هذه الطريقة في دراسة الجزيئات معروفة أكثر ، لذلك سأتحدث عنها باختصار أكثر قليلاً ، باستخدام التعديل الأكثر حداثة كمثال: مطياف تحويل فورييه (كما هو الحال في روسيا ، باختصار مطياف ميكروويف ذي تحويل فورييه).
التصميم هنا أكثر تعقيدًا بالفعل ، لأنه يتطلب مجموعة من الإلكترونيات المختلفة (مكبرات الصوت ومعدلات التردد ، وما إلى ذلك). سنحذف كل هذا ونتحدث فقط عما يحدث داخل غرفة الفراغ.
- مقابل بعضهما البعض هناك هوائيان بوقان (مثل الهوائي الذي افتتح دراسة relict ). يعمل أحدهم كجهاز إرسال ، والثاني هو جهاز استقبال.
- عمودي على هذه الهوائيات هو صمام يطلق العينة. في معظم الأحيان ، يتم إطلاقه في شكل بخار مع غاز حامل معين (غازات خاملة عادة) في وضع التوسع الحار. في ظل هذه الظروف ، تبرد الجزيئات بسرعة إلى درجات حرارة قريبة من 0 كلفن ، مما يبسط الطيف بشكل كبير ، مما يجعلها أكثر عرضة للتفسير.
- عندما تملأ الجزيئات الغرفة بأكملها ، يشعها هوائي الإرسال بإشارة معدلة بتردد خطي. في تمثيل التردد ، يتوافق هذا مع مجموع جميع الترددات في نطاق معين.
- تمتص بعض الجزيئات هذا الإشعاع بترددات إرسال مختلفة ، وتدخل في حالة مثيرة. ولكن ، بعد مرور بعض الوقت ، يتراجعون ، ويبدأون في إشعاع ما التقطوه أثناء الاندفاع من هوائي الإرسال. يبدو هذا المماطل بمثابة إشارة تذبذب متناقصة ( اضمحلال الحث المجاني ). يسجله الهوائي الثاني أيضًا. ثم ، بعد تحويل فورييه لتسجيل هذه الإشارة في الوقت المناسب ، يتم الحصول على طيف التردد المعتاد.
على النقيض من حيود الإلكترون ، الذي لم يكن مهمًا نوع الجزيئات التي يجب مراعاتها ، في مطياف الموجات الدقيقة ، يجب أن يكون للجزيء عزم ثنائي القطب ثابت (في حالات نادرة ، تكون عزم ثنائي القطب المغناطيسي مناسبًا أيضًا ، وهذا نموذجي للجذور ، مثل جزيء O
2 ). الإشارة هنا هي "كثافة الانبعاثات مقابل. التردد ". يتم استخلاص الثوابت الدورانية من هذه الأطياف من خلال بعض النماذج ، والتي يتم بعدها استخراج التركيب الجزيئي.
مرحبًا بكم في حديقة حيوانات المعلمات الجزيئية!
حان الوقت الآن للنظر في المعلمات الهندسية التي يمكننا الحصول عليها من التجارب المختلفة. في الواقع ، يشير كل نوع من أنواع الكميات إلى نوع النموذج الذي تم استخدامه لتناسب الإشارة التجريبية (غالبًا باستخدام طريقة المربعات الصغرى). يمكن العثور على معظم هذه المعلمات في مراجعة Kuchitsu K.، Cyvin SJ // In: Molecular Structure and Vibrations / Cyvin SJ (Ed.) - Amsterdam: Elsevier، 1972. - Ch.12. - ص.183-211.
لنبدأ مرة أخرى بالتصوير الإلكتروني.
- rg= langler rangleT هيكل. هذه مجرد مجموعة من متوسط قيم المسافات بين الذرات عند درجة حرارة معينة.
- ra= langler−1 rangle−1T هذه القيمة متشابهة rg ، ولكن من الطبيعي إلى حد ما وصف نمط الانعراج.
- r alpha=rh،0=؟ . هذه القيمة ليس لها معنى مادي واضح وهي مرتبطة بالكامل بالنموذج التفسيري. في الواقع ، هذا هو ما لوحظ في علم البلورات.
مثال بلوري r alpha الهياكل (رباعي النتروجين في البلورة). مقتبس من DOI: 10.1002 / anie.201704396
يتم تقريب كل ذرة بواسطة القطع الناقص الذي يصف حركتها الاهتزازية ، ويتم أخذ المسافات بين مراكز القطع الناقص كمسافات بين الذرات. لكن ، مثل هذا التبسيط لطبيعة حركة الذرات يتوافق مع إدخال تقريب المذبذب التوافقي للتذبذبات ، ولا يعمل دائمًا بشكل جيد.
مثال على توزيع الذرات عندما لا يعمل تقريب المذبذب التوافقي. نفس الرباعي ميثان ، ولكن في الغاز.
- rh1=؟؟؟ . لم يتم وصف حوت السمك معجزة اليودو
HEX باختصار ، وله علاقة ضعيفة جدًا بالواقع ، ولكن له خصائص رائعة: يجب أن يكون متسقًا هندسيًا (انظر أدناه) ويمكن حسابه بسهولة. ونتيجة لذلك ، اكتسبت شعبيتها الكبيرة في المجتمع الإلكتروني.
في مطيافية الموجات الدقيقة ، هناك متغيرات هيكلية أقل بقليل.
- الأكثر فهمًا جسديًا هو rn= langlen| hatr|n rangle هيكل. في الواقع ، هذا هو متوسط الهندسة على حالة اهتزاز معينة للجزيء ( |n rangle ) نظرًا لأنها تعمل في الغالب مع الجزيئات الباردة ، فإنها عادة ما تلاحظ بنية معينة من هذه الفئة: r0 ، أي هندسة الجزيء في حالة الذبذبات الأرضية ، عندما تصنع الذرات صفرًا من الاهتزازات حول موقعها الأكثر فائدة.
- الأكثر شعبية rs هيكل. الحرف "s" يعني "الاستبدال". يحصلون عليها بهذه الطريقة: يعتقدون أن هناك بعض إحداثيات الذرات التي يتم إصلاحها في الفضاء ، ثم يقومون باستبدال نظري ذري واحد للذرة في الجزيء ، ويحددون موضع هذه الذرة عن طريق تغيير الثوابت الدورانية. الميزة الرئيسية لهذه التكنولوجيا هي البساطة. ناقص: تحتاج فقط إلى استبدال أحادي + لا يمكن إنشاء جميع مواضع الذرات مثل هذا + المعنى المادي لمثل هذا النموذج ليس واضحًا جدًا.
- التطور المنطقي rs الهياكل rm - الهياكل التي يتم الحصول عليها من التركيب بواسطة المربعات الصغرى ذات الوزن الكتلي. كما أنهم بحاجة إلى جزيئات بديلة نظيرية ، ولكن أي منها مناسب بالفعل.
وهذا أبعد ما يكون عن جميع أنواع الهياكل الممكنة ...
لكن
المُحاكي العظيم المستخدم في حزمة كيميائية كمومية معيارية (مثل
برنامج شركة Gaussian Evil Corporation ) عند استخدام تعويذة سحرية مثل "Opt" يحصل على ما يسمى "هندسة التوازن" ، أو
re هيكل. هذا هو التكوين الأمثل للنوى ، مما يقلل من الطاقة الإلكترونية للنظام. ويمكن أيضًا سحب هذه الهياكل من حيود الإلكترون والتحليل الطيفي الدوراني ، ولكن فقط للجزيئات الصغيرة جدًا والمتناظرة ، وبالاقتران مع طرق البحث الأخرى. حتى الآن لا يعمل.
وهكذا يطرح السؤال: هل من الصحيح المقارنة
re هيكل مع بعض التجريبية ، والنظر فقط في الأخطاء التجريبية؟
الجواب هنا بسيط:
لا ، من الضروري وضع خطأ إضافي على الاختلافات المنهجية المحتملة. ويمكن إعطاء مثال حي على ذلك: تأثير باستيانسين-مورينو (انظر المقالات
DOI: 10.1107 / S0365110060002557 و
DOI: 10.1107 / S0365110060002545 ).
لنفترض أن لدينا جزيء من النوع CX
2 (أي CO
2 ، CS
2 ، وما إلى ذلك). كما يجب أن نعرف من مسار كيمياء المدرسة ، فإن هذه الجزيئات لها بنية خطية (ذرات الكربون واثنان من chalcogenes على خط مستقيم واحد).
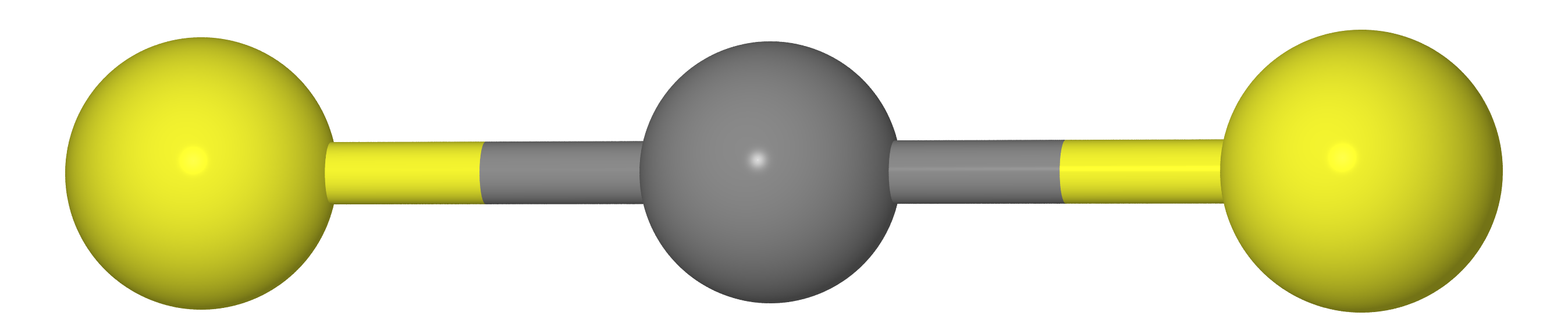
وهذا يعني أن المسافة بين ذرات X يجب أن تساوي ضعف طول الرابطة C - X (أي
re( mathrmXX)=2re( mathrmCX) )

على أي حال ، إذا قمنا بقياس المسافات بين الذرات C و X (
rg( mathrmCX) ) و XX (
rg( mathrmXX) ) عن طريق إلكترون الغاز ، نحصل على ذلك
rg( mathrmXX)<2rg( mathrmCX) ، أي يتحول الجزيء إلى انحناء. يكمن السبب في حقيقة أن الجزيء يقوم بما يسمى
اهتزازات المقص ، والتي بسببها تكون ذرات X أقرب كثيرًا من بعضها البعض في الموقع الأكثر ملاءمة (انظر الشكل أدناه).

من أين يأتي تأثير Bastansen-Morino. صورة من مقالة
DOI: 10.1039 / C6CP05849C .
لذلك ، إذا كنا نساوي متوسط درجة الحرارة
rg -بناء التوازن (
re ) ، سوف نخلص إلى استنتاج خاطئ بأن جزيئات ثاني أكسيد الكربون وثاني أكسيد الكربون منحنية.
لهذا السبب عند مقارنة أنواع مختلفة من المعلمات الهندسية ، يجب عليك دائمًا توخي الحذر الشديد. ينطبق هذا على كل من مقارنة البيانات التجريبية فيما بينها ، ومقارنة التجربة والنظرية.
الجزيئات نموذج الجزيئات القياسية
لنفترض الآن أننا نرغب تمامًا في محاكاة نتيجة بعض التجارب على أساس نموذجنا النظري من أجل مقارنة المحاكاة بالواقع في معركة عادلة.
وهنا من الضروري أيضا أن نكون حذرين ، لأنه نماذج مختلفة من الجزيئات لها حدودها للتطبيق. دعونا نفحص هذا باستخدام مثال نموذج الجزيء القياسي.
تحتاج أولاً إلى فهم النموذج القياسي للجزيء. يمتلك علماء فيزياء BAK نموذجهم
القياسي الخاص بهم ، ولدى علماء الفلك نموذجهم
الخاص ، ولدى علماء الفيزياء تصميمهم الأساسي الخاص بهم ، والذي يرقصون منه فيما بعد. ولكن على عكس النماذج المادية ، فإن ما نعتبره هو مجموعة من التقديرات التي تسمح للمستخدم بالحصول على النتيجة تلقائيًا وبسرعة نسبيًا.
لمستخدمي Gaussianنتذكر الآن ما يكمن في السحر السحري الغوسي "Opt" و "Freq".
يبدو المخطط العام للتقديرات المقدمة شيئًا مثل هذا:
نموذجنا القياسي هو في صميم الجودة. انتقل لفترة وجيزة من خلال جميع مراحل استلامها.
النموذج الناتج يسمى RR-HO (BO). لن نلمس تقريب بورن أوبنهايمر (BO) ، ولكن سيتعين علينا التحدث عن الدوار الصلب والمذبذب التوافقي في إطار الكيمياء الهيكلية ...والمشكلة الرئيسية في هذا التقريب هي أن الجزيء ليس صلبًا ، وأن اهتزازاته متناسقة تمامًا. وفقًا لذلك ، في الواقع ، نحن بحاجة إلى تقريب دوار غير صلب ومذبذب متناغم. والكلمة الرئيسية هنا هي "غير متناسقة" ، أي "ليست متناسقة".لنتحدث عن أبسط الجزيئات: ثنائي الذرة. هناك أمثلة كثيرة منها: HCl ، HBr ، HI ، CO ، O 2 ، N 2 ، إلخ. الخ
وتتميز عن جميع الجزيئات بحقيقة أن لديها اهتزاز واحد فقط: تمديد / ضغط المسافة بين الذرات.وهذه هي المسافة بين الذرات التي يمكننا قياسها في حيود إلكترون الغاز (في متغير متوسط درجة الحرارة ،rg ) وفي التحليل الطيفي الدوراني (المتوسط على سبيل المثال ، حالة الاهتزازات الأرضية ، أي r0 )
والآن يطرح السؤال الرئيسي عن كون الحياة وبشكل عام:ماذا سيكون rg و r0 في تقريب المذبذب التوافقي ، وكيف يمكن مقارنته بمسافة التوازن re ؟
للإجابة ، عليك أن تنظر إلى سطح الطاقة الكامنة لجزيء ثنائي الذرة:
- , : . , .
- , , 2 :
- ( r→0 ), - , « » ,
- ( r→+∞ )
ونتيجة لذلك ، إذا قام الجزيء بتقصير طول رابطه نسبةً إلى وضع التوازن ، فإنه يتاخم الحائط ، وإذا زاد ، فإنه يسقط على أريكة ناعمة. والجزيء ليس أحمق ، سوف يستلقي على الأريكة أكثر من الضرب على الحائط. لذلك ، سيكون متوسط الاهتزاز على مسافة أكبر من التوازن (re<r0,rg ) ، وهذا أمر ملحوظ: مثل هذه الإزاحة من 0.01 Å ، وهو أعلى من أخطاء القياس.
لذلك ، حتى إذا أردنا حساب شيء ما أشبه بالتجربة ، يبقى في إطار نموذج الجزيء القياسي (RR-HO @ BO) ، فلن نحصل على أي شيء جديد ، وبالتالي ، ستشارك هندسة التوازن في المقارنة.استنتاج الخطأ # 2
 رسم توضيحي من مقالة DOI: 10.1002 / anie.201611308 .والاستنتاج بسيط للغاية ويتكون من جزأين.
رسم توضيحي من مقالة DOI: 10.1002 / anie.201611308 .والاستنتاج بسيط للغاية ويتكون من جزأين.- مع المقارنة الصحيحة ، يجب أن يكون لجميع القيم نفس المعنى.
- إذا كانت القيم مختلفة ، فلا ينبغي نسيانها.
أمثلة على الأخطاء في الأوراق العلمية
"الأعمال الهندوسية"
في الواقع ، المكان الرئيسي حيث يمكنك العثور على هذا هو المجلات ذات المستوى المنخفض. نادرًا ما تحتوي على مقالات ذات نتائج رائعة ، لذلك تم اختيارها من قبل "الباحثين الرائدين" من دول العالم الثاني وأكثر (دول البريكس وأتباعها الأقل نجاحًا). من خلال مجلات "المستوى المنخفض" هنا لا تعني تلك التي تنشر مقالات مثل "The Rooter: Algorithm من أجل التوحيد النموذجي لنقاط الوصول والتكرار" ، بل المنشورات العلمية المحترمة. في مجال علمي ، أشهر "غسيل نصف" هي:(هناك آخرون). كما ترى ، وفقًا للإشارات الرسمية ، تعتبر العلوم الروسية منشورات لائقة جدًا. ولكن يأتي هناك اندفاع من ز ... محتوى نوعية مشكوك فيها، أن الكثير ما زال تسريب.على سبيل المثال ، أخذت العدد الأخير من مجلة البنية الجزيئية وذهبت إلى جدول المحتويات ، وفويلا:S. Sathiya ، M.Sinhilkumar ، C. Ramachandra Raja ، نمو Crystal ، تحليل سطح هيرشفلد ، دراسة DFT ودراسات NLO من الدرجة الثالثة من thiourea 4 dimethyl aminobenzaldehyde // J. Mol. هيكل. ، V. 1180 (2019) ، PP. 81-88.
https://doi.org/10.1016/j.molstruc.2018.11.067
الهيكل العام لمثل هذا العمل متواضع للغاية.- «» ( ) . .
- (), . — , ( , ) , . , - Gaussian, « ». … 1 2 , .. - .
- , /Vis, .
- في المرئيات الجزيئية القياسية ، مثل GaussView (الجريء) يتم رسم الصور الجميلة ، ولكن دائمًا بجودة رديئة.
- لم يتم استخلاص نتائج جوهرية: "لقد جربنا الكثير ، عدنا كثيرًا ، جلبنا الجداول والصور ⇒ نحن رائعون ، قدموا لنا الحلوى ".
ولكن من المفضلة: المادةتحقيق جوفينداراجان ، م. كاراباكاك ، FT-IR ، FT-Raman و UV. تحليل تقدير التردد المحسوب وحسابات البنية الإلكترونية على 1-nitronaphthalene // Spectrochimica Acta Part A: مطياف الجزيئات والجزيئات الحيوية ، V. 85 (2012) ، PP. 251-260 ،
https://doi.org/10.1016/j.saa.2011.10.002.
في ذلك ، تم تسجيل الطيف في المرحلة الصلبة بغباء ، ثم تم تفسيره على أساس الحسابات المتواضعة في نموذج HO في الطور الغازي. لكن الحيلة هي أنهم لم يتمكنوا حتى من إجراء حسابات عادية ، والتي ألمحوا إليها بأدب في التعليق على المقالة .ومع ذلك ، يشير مصطلح "الأعمال الهندوسية" (مثل مصطلح " رمز هندوسي ") إلى أبعد ما يكون عن الأعمال القادمة من شبه القارة الغامضة المقابلة.إذا ذهبت إلى موقع Cyberleninka الرائع ، فأنت تنظر إلى الهاوية ، وينظر إليك الهاوية ، يمكنك اكتشاف الكثير من الأشياء المثيرة للاهتمام. البحث عن "الكم من المواد الكيميائية» (ج / من دون شروط إضافية "PCA") كان قادرا على العثور على الكثير من الأشياء الشيطانمفيد. نظرًا لأن كمية كبيرة من الأعمال "الكمومية الكيميائية" قد كُرست لدراسة الخيول الكروية في فراغ (أي الحسابات دون الرجوع إلى الواقع) ، فلم تكن مرتبطة بهذا النص. ولكن من بينها ، فقدت هذه الأعمال الثلاثة:لقد سررت بشكل خاص بهذا الأخير ، لأن "تقييم الملاءمة" كان مقارنة غير كافية للهياكل في مراحل مختلفة (الغاز مقابل الكريستال) ومعاني مختلفة ( re مقابل rα ) - هذا هو بالفعل ارتفاع كفاية.هل يحدث في مجلات جيدة؟
نعم ، هناك "أخطاء" هناك.لا تخف ، انتهى كل شيء بشكل جيد!, , , / . , , .
, : , .
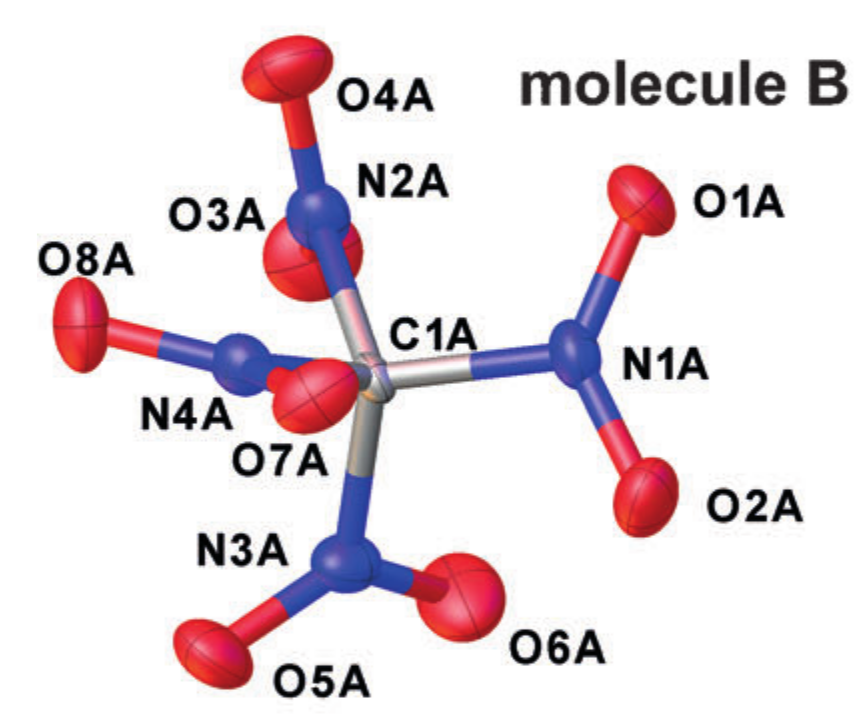
نحن نتحدث عن أحد الجزيئات العضوية ذات رابطة C - C مفردة للغاية: 1،1'-bisdiadamantane :
لماذا هذا الجزيء بارد,
(
), , C--C 1.54 Å.
, 1,1'-
re=1.630±0.005 Å, 0.08 Å ( )!
C--C - , , , , . , , () . - , . , ( ) , .
الاتصال المركزي الأحادي C - C طويل جدًا ، وبالتالي كان من المثير جدًا مقارنة كيفية إعادة إنتاج الأساليب النظرية للواقع. والحقيقة في المقالات الأولى ، ها هم:
القرف المقدس!— Nature, , — JACS — !!! , - .
تم تمثيله فقط عن طريق البيانات البلورية. ونتيجة لذلك ، بمقارنة الأشياء الصعبة القابلة للمقارنة مع بعضها البعض ، دون إجراء تصحيحات مناسبة للاختلاف في المعلمات ، توصلوا أخيرًا إلى استنتاج مفاده أن طول رابطة C - C المركزية في الغاز هو 1.655 Å ، متجاوزًا 0.02 Å. وهذا أكثر بكثير من الخطأ التجريبي.لحسن الحظ ، تعاونوا في النهاية مع المتخصصين في هذه القضايا ، وفي النهاية حصلوا على الإجابة الصحيحة ( يمكن أيضًا العثور على ملخص شعبي قصير لهذا العمل على N + 1 ).هل تريد مقارنة؟
 بعد كل ما كتبته عن صحة المقارنات ، قد يطرح سؤال معقول: هل من الضروري إذن مقارنة نتائج الحسابات ونتائج التجارب فيما بينها؟من الضروري! كما تحتاج!هناك بيان مشهور (لم أتمكن من العثور على مؤلف موثوق به):
بعد كل ما كتبته عن صحة المقارنات ، قد يطرح سؤال معقول: هل من الضروري إذن مقارنة نتائج الحسابات ونتائج التجارب فيما بينها؟من الضروري! كما تحتاج!هناك بيان مشهور (لم أتمكن من العثور على مؤلف موثوق به):لا أحد يصدق الحسابات النظرية ، باستثناء الشخص الذي قام بها.
الجميع يؤمن بالنتائج التجريبية ما عدا من حصل عليها.
عند ترجمتها إلى اللغة الروسية ، يبدو الأمر كما يلي: لا أحد يصدق الحسابات النظرية ، باستثناء الشخص الذي قام بها ، ولكن الجميع يصدق البيانات التجريبية ، باستثناء الشخص الذي تلقىها.لكن في العلم ، من الضروري أن يؤمن الجميع (جيدًا ، أو الأغلبية) ، والتجربة هي المقياس الوحيد ، لأنه يربط ما قمنا بحسابه بالواقع.هناك مقالة ملحوظة (الوصول المفتوح) في ثاني أهم مجلة كيميائية حول موضوع ما يجب أن يفعله الباحث أو الشخص العادي الذي يقرأ المقالات العلمية و / أو الأخبار: Mata R. ، Suhm M. // Angew. كيم. Int. إد. ، 56 (2017) ، دوى: 10.1002 / anie.201611308(بالمناسبة ، لقد أعطيت رابطًا لها بالفعل ، لأن صورة واحدة ، بواسطة ريكاردو ماتا ، من هذه المقالة).تقدم استنتاجات هذا المقال توصيات لمنظري المحاكاة والتجريب. سأقدمها هنا (في الترجمة ومراجعة صغيرة) ككلمة أخيرة لهذا المنشور.- يجب على المنظر:
- لا تقدم طرقًا ومحاولات ناجحة فحسب ، بل تصف أيضًا فشل الطرق (خاصة إذا كانت هذه الأساليب شائعة) ،
- وصف منهجيتك بشكل جيد وكامل ،
- حيث يمكن إعطاء تقديرات (أو وصف) للأخطاء ، وتقريبات وتبسيطات هامة مقبولة.
- المجربون بدورهم يجب أن:
- لكزة المنظرين بياناتهم التجريبية ، والتي يمكن استخدامها كمعايير (معايير) ،
- لإظهار البيانات التجريبية غير مفهومة للمجتمع العلمي ، حيث ستساعد النظرية (أو تجارب إضافية) في التفسير ،
- التحدث على
أرض أجنبية من المؤتمرات النظرية مع بياناتها ،
- سحب أشياء البيانات التجريبية الخاصة بك التي يمكن الوصول إليها قدر الإمكان للمقارنة مع النظرية ،
كل المقارنات الأفضل والصحيحة! وتذكر: فقط من لم يفعل شيئًا ليس مخطئًا.
PS
كنتيجة لاحقة ، أود أن أعطي قائمة صغيرة من قواعد البيانات حيث يمكنك حفر البيانات التجريبية المختلفة للجزيئات.بنوك البيانات الهيكلية
علب بلورية
أسهل طريقة لتحديد بنية الجزيء في البلورة هي الأنيسول الخماسي الكلور هو روتين. لذلك ، إذا كنت لا تعرف كيف يبدو الجزيء ، فانتقل إلى بنوك البيانات البلورية (الأماكن التي يتم فيها تجميع جميع هياكل المواد تقريبًا التي تم حشرها في مقياس الزوايا وإضاءتها بواسطة حزمة من جزيئات الموجة القصيرة). نظرًا لوجود الكثير من هذه البنوك ، سأقدم فقط أشهرها (يمكن العثور على قائمة أكثر اكتمالاً على ويكي ).- قاعدة بيانات الهيكل البلوري غير العضوي ( ICSD ). لا يتعلق هذا بالكامل بالجزيئات ، حيث يمكنك العثور على هياكل مختلفة من الأملاح والمعادن والسيراميك وما إلى ذلك. هذه القاعدة مدعومة من جامعة كارلسروهيف للتكنولوجيا ، وبالتالي فإن الوصول إليها مدفوع وغير رخيص. ولكن إذا كان ذلك ، موقعها .
- Cambridge Structural Database ( CSD ). , . ! . ! . , , , , . .
- Crystallography Open Database ( COD ). - . , , , , . .
- , , Protein Data Bank ( PDB ). , ( ). .
هيكل الجزيئات في الغاز
هنا الأمور أسوأ إلى حد ما ، لأن التجارب لدراسة بنية الجزيئات الحرة أكثر تعقيدًا بكثير ، سواء لتنفيذ (على الأقل فراغ عالي) وللتفسير.لذلك ، هناك قواعد بيانات أقل بكثير.- أكبر قاعدة بيانات للجزيئات الحرة هي MOlecular GAsphase DOCumentation (أو MOGADOC ). يقع مقرها في جامعة أولم ، وهي استثمار باهظ الثمن. ولكن ، إذا كان أي شيء ، فإن الموقع هنا .
- إذا كنت تريد معرفة هياكل التوازن التجريبية 100٪ للجزيئات ، فهذه هي مقارنة NIST للكيمياء الحاسوبية وقاعدة البيانات المعيارية ( CCCBDB ). تقريبا كلها تجريبية بحتةre - , . .
- — MolWiki . , , , ( ). .
?
 مأخوذة من xkcd.comهناك قواعد بيانات أكثر بكثير هنا ، حيث أن إزالة الطيف بدون تفسير مهمة أبسط بكثير من الحصول على هيكل (لا حاجة إلى بناء نماذج وإثبات أنها صحيحة). بالإضافة إلى ذلك ، فإن الأطياف ذات قيمة تطبيقية رائعة: يمكن استخدامها لتحديد تركيبة العينات ، سواء كانت مياه من نهر مجاور ، أو إشارة من سحابة جزيئية (أو حتى من جو كوكب خارجي ، انظر الشكل أعلاه).نعم ، بالمناسبة ، جميع الروابط في هذا القسم ستكون مجانية لقواعد البيانات.
مأخوذة من xkcd.comهناك قواعد بيانات أكثر بكثير هنا ، حيث أن إزالة الطيف بدون تفسير مهمة أبسط بكثير من الحصول على هيكل (لا حاجة إلى بناء نماذج وإثبات أنها صحيحة). بالإضافة إلى ذلك ، فإن الأطياف ذات قيمة تطبيقية رائعة: يمكن استخدامها لتحديد تركيبة العينات ، سواء كانت مياه من نهر مجاور ، أو إشارة من سحابة جزيئية (أو حتى من جو كوكب خارجي ، انظر الشكل أعلاه).نعم ، بالمناسبة ، جميع الروابط في هذا القسم ستكون مجانية لقواعد البيانات.- NIST Chemistry WebBook . , . , UV/Vis, - . , ! , , . .
- High-resolution transmission molecular absorption database ( HITRAN ). - , , , , (, ). .
- , The Cologne Database for Molecular Spectroscopy, . .
- حسنًا ، كمثال أخير ، سأقدم مشروع ExoMol . هذه ليست أطيافًا تجريبية نقية تمامًا ، ولكن هذا مثال ممتاز لتفاعل النظرية والتجربة: استنادًا إلى البيانات التجريبية عالية الدقة والحسابات عالية المستوى للغاية ، يتم توقع أطياف الجزيئات البسيطة في ظل ظروف مختلفة (بما في ذلك الحالات الشديدة). ينصب التركيز الرئيسي هنا على المؤشرات الحيوية ، لذلك عندما يرى الفلكيون أطياف الكواكب الخارجية ، يمكنهم بسهولة تحديد الجزيئات التي نعرفها بالفعل. الموقع .
PPS
إذا كانت هناك أخطاء / شيء لا يزال غير مفهوم ، فاكتب في التعليقات - سأصحح / أحاول أن أشرح بشكل أفضل.