تطبيق عملي لمولد التحويل باستخدام Verilog HDL

مجردة

تعد سجلات إزاحة الملاحظات الخطية أداة ممتازة لتنفيذ مولد بت عشوائي زائف في الأجهزة ؛ أنها تمنع بنية إلكترونية بسيطة وفعالة. علاوة على ذلك ، فهي قادرة على إنتاج تسلسل الإخراج مع فترات كبيرة وخصائص إحصائية جيدة. ومع ذلك ، فإن LFSRs القياسية ليست آمنة تشفيرًا ، حيث يمكن توقع تسلسل الإخراج بشكل فريد نظرًا لوجود عدد صغير من بتات الدفق الرئيسية باستخدام خوارزمية Berlekamp-Massey. تم اقتراح عدة طرق لتدمير الخطية المتأصلة في تصميم LFSR. تتضمن هذه الطرق مولدات توليفة غير خطية ومولدات ترشيح غير خطية ومولدات تعمل على مدار الساعة. ومع ذلك ، فإنها تظل عرضة للعديد من الهجمات مثل هجمات القنوات الجانبية والهجمات الجبرية. في عام 2015 ، تم اقتراح مولد جديد متحكم زمنياً يسمى مولد التبديل. ثبت أن هذا المولد الجديد مقاوم للهجمات الجبرية وهجمات القنوات الجانبية ، مع الحفاظ على الكفاءة والمتطلبات الأمنية. في هذا المشروع ، نقدم تصميم مولد التبديل باستخدام Verilog HDL.

مقدمة والخلفية التاريخية

يرتبط تاريخ توليد الأرقام العشوائية الزائفة في الأجهزة ارتباطًا وثيقًا بتطوير الأصفار الدائرية. الأصفار المتدفقة هي الأصفار التي تقوم بتشفير أحرف النص العادي بشكل فردي (عادةً بتأثيرًا تدريجيًا) ، على النقيض من منع الأصفار ، التي تقوم بتشفير النص العادي في كتلة كبيرة (64 بت أو أكثر). تتطلب العديد من بنيات تشفير الدفق مولد تيار رئيسي ، وهو عبارة عن مولد بت عشوائي شبه زائف والذي يكون مفتاح التشفير هو مفتاح التشفير. لكل بت نص عادي ، يتم حساب بت النص المشفر المقابل كدالة قابلة للإرجاع (عادةً بوابة xor) من بت النص العادي وبت بت دفق المفتاح المقابل. لذلك ، فإن تصميم مولدات تيار آمنة وفعالة أمر ضروري لتشغيل تشفير الدفق.


إحدى الأدوات المفيدة لبناء مولدات التيار الرئيسي هي سجلات تحويل الملاحظات الخطية. يمكن تركيبها بسهولة باستخدام مكونات إلكترونية أولية ، ويمكن برمجتها ببساطة على أجهزة منطق قابلة للبرمجة. أيضًا ، نظرًا لتركيبها البسيط ، يمكن تصميم نماذج LFSR وتحليلها رياضيا ، مما أدى إلى مجموعة كبيرة من المعرفة والنتائج المتعلقة بها. يحتوي تسلسل خرج LFSR الذي تم إنشاؤه بشكل صحيح على طول أسي وخصائص statisitical جيدة مثل التعقيد الخطي الكبير.


على الرغم من الخصائص الإحصائية الجيدة لل LFSR ، لا يمكن استخدامه كمولد تيار رئيسي في شكله المستطيل بسبب طبيعته الخطية. إذا تمكن المهاجم من معرفة $$$2L$بتات تيار المفتاح المتتالية ، ثم يمكن توقع تسلسل الإخراج بشكل فريد وفعال باستخدام خوارزمية Berlekamp-Massey ، حيث $$$L$هو عدد السجلات. تم اقتراح العديد من الطرق المختلفة لتدمير الخطية الكامنة في تسلسل إخراج LFSR:

• استخدام LFSRs متعددة ووظيفة الجمع غير الخطية لمخرجاتها (مولدات توليفة غير خطية).
• توليد تسلسل الإخراج كدالة غير خطية لحالة LFSR (مولدات التصفية غير الخطية).
• قطع مسافة زمنية غير منتظمة لل LFSRs (المولدات التي تسيطر عليها على مدار الساعة).

ومع ذلك ، ظلت كل هذه التصميمات عرضة للهجمات مثل الهجمات الجبرية والقنوات الجانبية. بعد عام 2000 ، لم تعد هذه مشكلة حرجة ، حيث تم اقتراح تشفير الكتلة Rijndael وانتخابه كمعيار متقدم للتشفير (AES). كانت AES قادرة على العمل في وضع تشفير الدفق وتفي بجميع المعايير الصناعية لشفرات الدفق. علاوة على ذلك ، مع ظهور القوى الحسابية ، يمكن نشر AES على منصات مختلفة. وقد أدى ذلك إلى انخفاض كبير في تطبيقات تشفير الدفق.


قدم عدي شامير محاضرة مدعوة في كتاب "حالة الفن" في Stream Ciphers 2004 و Asiacrypt 2004 بعنوان "Stream Ciphers: Dead or Alive؟". في عرضه التقديمي ، اقترح أن الأصفار تيار يمكن البقاء على قيد الحياة في التطبيقات التالية:

• تطبيقات موجهة نحو البرمجيات بسرعات عالية للغاية (مثل أجهزة التوجيه).
• تطبيقات موجهة للأجهزة مع مساحة صغيرة بشكل استثنائي (مثل البطاقات الذكية).

واحد من أحدث المقترحات لمولدات التيار الرئيسي هو مولد التبديل. يزعم أنه مقاوم للهجمات الجبرية والقنوات الجانبية ، مع الحفاظ على الكفاءة وسرعات التشغيل.


في هذا المشروع ، سنقدم تصميمًا لمولد التبديل في الأجهزة ، باستخدام Verilog HDL. أولاً ، نقدم النموذجين الشائعين لـ LFSRs ، فيبوناتشي LFSRs و Galois LFSRs. بعد ذلك ، نقدم عرضًا رياضيًا لل LFSRs. ثم سنقدم مولد التبديل كما قدمه. أخيرًا ، نقدم تصميم Verilog لمولد التحويل.

الخطي ردود الفعل التحول السجلات

سجلات إزاحة الملاحظات الخطية عبارة عن دوائر تتكون من قائمة سجلات خطية (وتسمى أيضًا عناصر التأخير) ومجموعة محددة مسبقًا من الاتصال فيما بينها. تتحكم إشارة الساعة العالمية (الفردية) في تدفق البيانات داخل LFSR. النوعان الأكثر شيوعًا من LFSRs هما فيبوناتشي LFSRs و Galois LFSRs ؛ تأجيل فقط في شكل اتصالات. كما سنرى لاحقًا في قسم النماذج الرياضية ، هناك العديد من أوجه التشابه بين بنيات فيبوناتشي وجالوا ، ويفضل أحدهما على الآخر تطبيق معين.


من خلال هذه المقالة ، نفترض عدادًا افتراضيًا للوقت العالمي يبدأ من $$$0$وزيادة بنسبة $$$1$بعد كل حافة إيجابية من دورة الساعة العالمية.

سجلات

السجل هو عنصر منطقي قادر على تخزين جزء واحد من البيانات ، يسمى الحالة. لديها اثنين من خطوط الإدخال: خط البيانات بت واحد وخط إشارة على مدار الساعة. لديها إخراج بت واحد يساوي دائمًا الحالة الداخلية. على كل حافة موجبة لإدخال الساعة ، يتم تعيين إدخال البيانات إلى الحالة ، وإلا تظل الحالة على حالها. دعنا نشير إلى حالة السجل $$$S$في الوقت $$$t$كما $$$\ mathop S \ nolimits ^ t$.

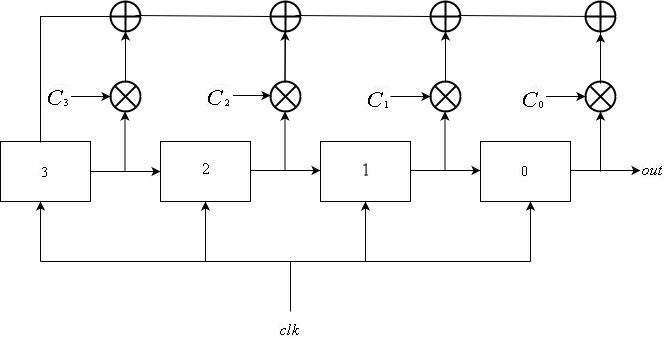
فيبوناتشي

يتكون فيبوناتشي LFSR من $$$L$السجلات التي تم تعدادها من $$$0$ل $$$L-1$، كل متصلا إشارة الساعة نفسها. مدخلات التسجيل $$$i$هو إخراج التسجيل $$$i + 1$ل $$$0 \ le i \ le L-2$. ردود الفعل المدخلات للتسجيل $$$L-1$هو مجموع المخرجات xor لمجموعة فرعية من السجلات. يمكن وصف تحديث السجل رياضيا كما يلي:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ start {array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {if} \ \} 0 \ le i \ le L-2 \\ \ mathop \ bigoplus \ limit_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ right.$$

اين $$$C_j = 1 دولا$إذا سجل $$$j$يتم تضمينها في ردود الفعل و $$$0$خلاف ذلك.

يتم الحصول على تسلسل الإخراج من السجل $$$0$. وهذا هو ، تسلسل الإخراج هو $$$\ mathop {\ left \ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

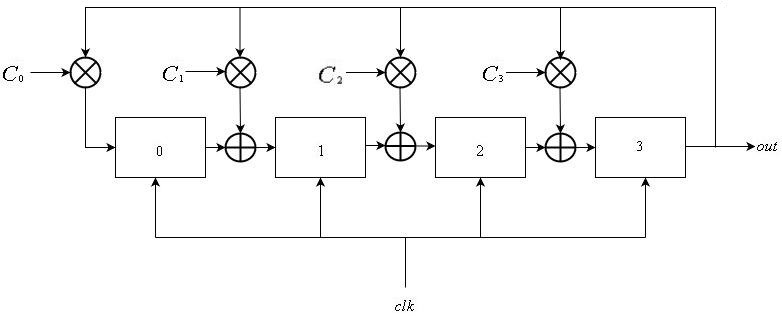
جالوا LFSRs

غالوا LFSRs تتكون أيضا من قائمة خطية من $$$L$السجلات التي تم تعدادها من $$$0$ل $$$L-1$، كل تقاسم إشارة الساعة العالمية. مدخلات التسجيل $$$i$هو إخراج التسجيل $$$i-1$ل $$$1 \ le i \ le L-1$. بالنسبة إلى مجموعة فرعية من السجلات ، يتم إدخال مدخلاتهم مع إخراج التسجيل $$$L-1$. يمكن التعبير عن ذلك على النحو التالي:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ start {array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ \ if \ \}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \}} i = 0 \ end {array} \ right.$$

اين $$ إذا كان إدخال التسجيل $$$i$هو xored مع إخراج التسجيل $$$L-1$.


بطريقة مشابهة لطريقة LFSRs فيبوناتشي ، يتم تعريف تسلسل الإخراج كـ $$$\ mathop {\ left \ {{\ mathop S \ nolimits_ {L-1} ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

مقارنة بين تصاميم فيبوناتشي وجالوا

هناك مراسلات مباشرة بين فيبوناتشي وجالوا LFSRs بالمعنى الرياضي ، كما سنرى في القسم التالي. ومع ذلك ، هناك ميزتان ملحوظتان لاستخدام تصميم Galois:

• في تنفيذ البرامج ، فإنه لا يتطلب $$$L$تحقق التكافؤ قليلا ، والذي يضيف عامل لوغاريتمي من التعقيد.
• في تنفيذ الأجهزة ، لا يتطلب الأمر سوى بوابات xor ثنائية الإدخال ، والتي يكون تأخير نشرها أقل بكثير من بوابات xor متعددة المدخلات المستخدمة في تصميم Fibonacci.

في مشروعنا ، نأخذ بعين الاعتبار صياغة المصفوفة الخاصة بـ LFSR ، بحيث يمكن تغيير كلا المعماريين.

نموذج رياضي من LFSRs

في الأقسام التالية ، ما لم يُنص على خلاف ذلك ، نفترض أن كل العمليات الحسابية تتم تحت حقل جالوا $$$Gf \ left (2 \ right)$. وهذا هو ، يتم حساب جميع العمليات مودولو $$ . تطبيق آخر لهذه الاتفاقية هو أن كل الضرب منطقي وبوابة ، وكل الجمع هو بوابة xor.


النظر في حالات الجميع $$$L$سجلات LFSR في بعض الوقت $$$t$؛ هذا يمكن أن يمثله ناقل من $$${\ left \ {{0،1} \ right \} ^ L}$ :

$$

$${S ^ t} = \ left ({\ mathop S \ nolimits_0 ^ t؛ \ mathop S \ nolimits_1 ^ t؛ \ ldots؛ \ mathop S \ nolimits_ {L-1} ^ t} \ right)$$

نشير إلى هذا المتجه باعتباره حالة LFSR. لاحظ أن هناك على الأكثر $$${2 ^ L}$الدول الممكنة ل $$$L$تسجيل LFSR. لاحظ أيضًا أنه إذا كان LFSR سيصل إلى حالة الصفر ، فلن يتمكن من الوصول إلى أي حالة أخرى. لذلك نقول أن هناك $$$2 ^ L-1$غير تافهة من LFSR.


النظر في التحول الخطي التالي:

$$

$$F = \ left ({\ start {array} {* {20} {c}} 0 & 1 & \ cdots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \\ {\ mathop C \ nolimits_0} & {\ mathop C \ nolimits_1} & \ cdots & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

بالنظر إلى ذلك $$$\ mathop S \ nolimits ^ t$هي حالة فيبوناتشي LFSR ، ويمكن ملاحظة ذلك

$$

$$F \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

إذا $$$\ mathop S \ nolimits ^ t$كان حالة من Galois LFSR ، ثم النظر في tranformation $$$G$:

$$

$$G = \ left ({\ start {array} {* {20} {c}} 0 & \ cdots & 0 & {\ mathop C \ nolimits_0} \\ 1 & \ cdots & 0 & {& mathop C \ nolimits_1} \\ \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 1 & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

في هذه الحالة ، لدينا

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

يمكن أن تكون تمثيلات مصفوفة LFSR مرنة عند التعامل مع التحديثات المتكررة ، حيث يمكن تفسيرها على أنها منتج مصفوفة بسيط. ويمكن ملاحظة ذلك $$$F = {G ^ T}$. تشير هذه الحقيقة إلى العديد من أوجه التشابه بين تصميمات Fibonacci و Galois إذا تم اعتبارها تحولات خطية من $$${\ left \ {{0،1} \ right \} ^ N}$ ل $$${\ left \ {{0،1} \ right \} ^ N}$ .


يُعرف ضرب متجه حالة بعض LFSR بواسطة مصفوفة (لأنواع Fiboancci أو Galois) باسم تسجيل LFSR أو تحديثه.

مولد التبديل

إن Switching Generator عبارة عن مولد يتم التحكم فيه على مدار الساعة تم اقتراحه في عام 2015. وقد ثبت أنه يتمتع بمقاومة للهجمات الجبرية والقنوات الجانبية. في هذا القسم ، سنقدم تصميم مولد التبديل ، كما هو محدد من قبل مخترعيها.

الهيكل الأساسي

يتكون مولد التبديل من LFSRs اثنين: عنصر تحكم LFSR $$$دولا$من الطول $$$N$و LFSR البيانات $$$B$من الطول $$$M$. يتم تحديث التحكم LFSR كما هو موضح سابقا. ومع ذلك ، يتم تحديث البيانات LFSR باستخدام واحدة من اثنين من المصفوفات المحتملة ، $$$\ mathop M \ nolimits_1 ^ i$او $$$\ mathop M \ nolimits_2 ^ j$اين $$${M_1} ، {M_2}$مصفوفات مصاحبة لبعض الحدود المتعددة البدائية. يتم تحديد اختيار مصفوفة واحدة على الأخرى من خلال خرج إشارة من السيطرة LFSR. يمكن وصف هذه العملية كما يلي:

$$

$$\ mathop B \ nolimits ^ t = \ left \ {\ start {array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \ right.$$

إخراج مولد التبديل هو إخراج LFSR $$$B$. لاحظ أننا افترضنا ذلك $$$دولا$هو جالوا LFSR. يمكن أن يكون كذلك فيبوناتشي LFSR.


أعداد صحيحة $$$i، j$تسمى مؤشرات التبديل.

البذرة

أذكر أن LFSR يمكن أن تتكرر من خلال على الأكثر $$${2 ^ L} -1$الدول غير تافهة قبل إعادة النظر في الدول السابقة. منذ المصفوفات $$${M_1} ، {M_2}$هي مصفوفات التحول من LFSRs ، يمكننا استنتاج أن الأعداد الصحيحة $$$i، j$يمكن أن يكون على الأكثر $$$2 ^ M-1$قبل البدء في تكرار المصفوفات.


البذور لمولد التبديل هو $$$N + 3M$بت ، تمثل الحالات الأولية لـ LFSRs $$$دولا$و $$$B$والقوى الصحيحة $$$i، j$. لاحظ أن المصفوفات $$${M_1} ، {M_2}$يتم إصلاحها طوال فترة التنفيذ ولا يتم تضمينها في البذور.

فيريلوج التصميم

في هذا القسم ، سنقدم تصميمنا لمولد التحويل باستخدام Verilog HDL. سوف نقدم كل تصميم وحدة في أسفل الأزياء. في النهاية ، نقدم وحدة مولد التبديل.


في تصميمنا ، حاولنا الحفاظ على المكونات المتزامنة عند الحد الأدنى. المكونات الوحيدة التي تسيطر عليها على مدار الساعة هي LFSRs $$$A ، B$.


يمكن تنفيذ عمليات المصفوفة والمتجهات بعدة طرق مختلفة ، متفاوتة في استهلاك وحدات المنطق ووحدات الذاكرة والتعقيد الإجرائي. في تصميمنا ، نلغي الحاجة إلى الكتل الإجرائية ، ونستخدم عناصر المنطق إلى الحد الأقصى.


تتم فهرسة جميع المصفوفات في الوحدات التالية بدءًا من $$$0$من اليسار إلى اليمين ، ثم من أعلى إلى أسفل.


لاحظ أيضًا أن جميع الوحدات النمطية لها أحجام معلمة ؛ هذا لأغراض التصحيح. في التنفيذ الفعلي ، يتم إصلاح جميع الأحجام.

معدد

هذه هي وحدة تنفيذ 2 إلى 1 $$$N$بت المضاعف. وحدة لديها اثنين $$$N$خطوط إدخال بت ، خط اختيار 1 بت ، و $$$N$خط الانتاج بت. إذا كان الإدخال محدد $$$0$ثم يتم تعيين الإخراج إلى سطر الإدخال الأول ، وإلا فإنه يتم تعيينه إلى الثاني.


وحدة المضاعف

تحول المتجهات

تطبق هذه الوحدة تحولًا خطيًا على ناقل. يقبل كمدخل $$$N \ مرة N$مصفوفة التحول و $$$N$ناقلات بت. إنه يخرج منتج مصفوفة المتجه من مدخلاته.


كل بت في متجه الإخراج هو نتيجة ل $$$N$بوابة xor بت ، مع الأخذ في الاعتبار نتيجة ل $$$N$بت bitwise وموجه المتجه والصف المصفوفة المقابلة. وهذا يعني أن كل بت ناتج يتم إدخاله على الإدخال ، ولا توجد حاجة إلى كتل إجرائية.


بالضبط $$$N ^ 2$يتم استخدام اثنين من المدخلات والبوابات ، جنبا إلى جنب مع $$$N$$$$N$المدخلات بوابات xor.


وحدة تحويل المتجهات

الهوية

هذه الوحدة لا تقبل أي مدخلات. لها $$$N \ مرة N$يتم تهيئة الإخراج بت إلى $$$N$مصفوفة الهوية. تم الإعلان عن مثل هذه الوحدة من أجل الراحة ، بحيث لا يتعين علينا تهيئة متجه سجل عالمي لكل حجم مختلف.


وحدة مصفوفة الهوية

تبديل

هذه الوحدة تقبل $$$N \ مرة N$المصفوفة وإخراج تبديل لها. لا يتم استخدام عناصر منطقية ولا عناصر ذاكرة في هذه الوحدة ، حيث أن مخرجاتها هي مجرد تبديل لمدخلاتها
.

مصفوفة تبديل وحدة

مصفوفة الضرب

هذه هي وحدة تنفيذ الضرب مصفوفة المصفوفة. يقبل اثنين $$$N \ مرة N$المصفوفات كمدخلات ، ومخرجات مصفوفة المصفوفة.


تحتوي هذه الوحدة على مثيل لوحدة تبديل المصفوفة. هذا يجعل من الممكن تخصيص مؤشرات متتالية للأعمدة في مصفوفة الإدخال الثانية. ثم يتم تعيين كل إدخال في مصفوفة الإخراج إلى إخراج $$$N$- مدخل بوابة xor ، الذي يكون إدخاله هو bitwise والصف المقابل من المصفوفة الأولى والعمود من الثاني.


بالضبط $$$N ^ 3$اثنين من المدخلات والبوابات و $$$N ^ 2$$$$N$يتم استخدام الإدخال xor في هذا التطبيق.


مصفوفة وحدة الضرب

مصفوفة الأس

ترفع هذه الوحدة مصفوفة إلى عدد صحيح. يقبل كمدخل $$$N \ مرة N$مصفوفة و $$$K$عدد صحيح بت. ناتجها هو المصفوفة التي أثيرت على قوة عدد صحيح المحدد.


مصفوفة وحدة الأس

وحدة التحكم

هذه الوحدة تنفذ $$$N$بت التحكم LFSR. إنها واحدة من وحدتي التحكم على مدار الساعة في تصميمنا.


ويشمل ثابت $$$N \ مرة N$مصفوفة التحول LFSR ومتغير $$$N$الدولة بت. يتضمن مدخلاته ساعة ، و $$$N$إعادة تعيين حالة بت ، وإشارة إعادة تعيين. ناتجها هو بت واحد ، وهو الجزء الأخير من LFSR.


بعد كل حافة إيجابية لإشارة الساعة ، يتم تحديث الحالة وفقًا لمصفوفة التحويل باستخدام وحدة الضرب بمصفوفة المتجهات. يتم تعيين إعادة تعيين الحالة إلى الحالة الداخلية بعد كل حافة إيجابية من إشارة إعادة التعيين.





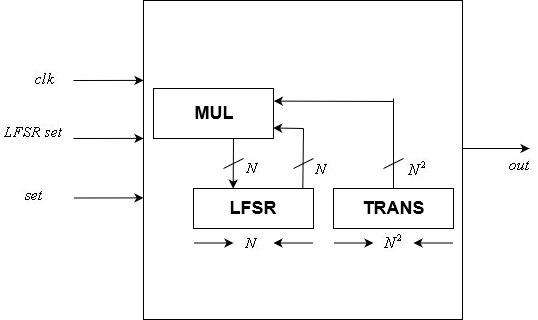وحدة التحكم وحدة

وحدة البيانات

ال $$$N$يتم تطبيق LFSR البيانات باستخدام هذه الوحدة. مثل وحدة التحكم ، يتم التحكم به على مدار الساعة


وحدة تضم اثنين $$$N \ مرة N$المصفوفات التحول و $$$N$دولة بت LFSR. يقبل كمدخل إشارة ساعة ، إشارة تحكم ، $$$N$بت إعادة تعيين حالة LFSR ، اثنان $$$N \ مرة N$إعادة تعيين مصفوفة التحول ، وإشارة إعادة تعيين. لديها ناتج واحد بت ، والجزء الأخير من LFSR الداخلية.


لاحظ أنه نظرًا لأنه يمكن تغيير البذرة ، يمكن أيضًا تغيير مصفوفات التحويل ، على عكس وحدة التحكم التي تكون مصفوفة التحويل بها ثابتة.




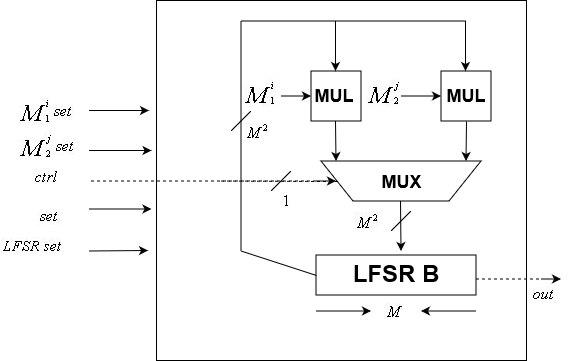\ وحدة البيانات

مولد التبديل

هذه هي الوحدة الرئيسية لتصميمنا. هو معلمات من قبل الأعداد الصحيحة $$$N ، M$، والتي هي أحجام وحدات التحكم والبيانات ، على التوالي.


المدخلات إلى هذه الوحدة هي إشارة على مدار الساعة ، أ $$$N + 3M$البذور بت ، وإشارة مجموعة. البذرة هي ببساطة سلسلة من التحكم LFSR إعادة تعيين ، إعادة تعيين LFSR البيانات ، والأعداد الصحيحة $$$i، j$الناتج هو واحد بت ، بت العشوائية الزائفة الناتجة عن مولد التبديل.


هذه الوحدة تضم اثنين $$$M \ مرة M$المصفوفات $$$\ mathop M \ nolimits_1 ، \ mathop M \ nolimits_2$. يتم إصلاح هذه المصفوفات طوال فترة التنفيذ.


يتم استخدام مثيلين لوحدة الأس الأسس لحساب مصفوفات الإدخال لوحدة البيانات ، حيث تكون مدخلاتهما هي مصفوفات التحويل الصحيحة والأعداد الصحيحة $$$i، j$، المستخرجة من البذور.


وحدة مولد التبديل

الاستنتاجات والتوصيات

في هذا المشروع ، قدمنا ​​تصميم مولد التبديل باستخدام Verilog HDL. يركز هذا التصميم بالكامل على الأجهزة ، ويزيل استخدام الكتل الإجرائية. مثل هذا النهج يسمح لأداء الحد الأقصى على حساب عناصر المنطق والذاكرة. بالنسبة لبعض التطبيقات ذات قيود عناصر المنطق والذاكرة ، قد يكون من المفيد التضحية بالأداء وزيادة استخدام الكتل الإجرائية لتقليل استخدام العناصر الإلكترونية.


من عيوب المشروع أنه يتحمل مسؤولية اختيار مؤشرات التبديل الجيدة على المستخدم. أحد التطورات المحتملة هو إضافة مكون جهاز للتحقق من صحة فهرس التبديل المستخدم. وهذا يتطلب تنفيذ خوارزميات معقدة للأجهزة مثل العثور على خصائص متعددة الحدود لمصفوفة معينة والتحقق من أنها بدائية.


هناك تقدم محتمل يتمثل في إضافة مولد أرقام عشوائي حقيقي للتحقق من مؤشرات التبديل العشوائي ، وإخراج زوج صالح بمجرد العثور عليه. يمكن إثبات أن هذه العملية تتوقف بعد فترة قصيرة مع احتمال كبير.

المراجع

1. كاتز ، جوناثان ، وآخرون. كتيب التشفير المطبق. مطبعة CRC ، 1996.
2. تشوي ، جون ، وآخرون. "مولد التبديل: مولد جديد يتم التحكم فيه على مدار الساعة مع مقاومة ضد الهجمات الجبرية والقنوات الجانبية." Entropy 17.6 (2015): 3692-3709.
3. شامير ، عدي. "الأصفار تيار: ميتا أو حيا؟" أسياكريبت. 2004
4. LFSRs للمبتدئين