كُتب المقال عن تحليل ودراسة مواد المسابقة للبحث عن السفن في البحر.

دعنا نحاول أن نفهم كيف وماذا تبحث الشبكة وماذا تجد. هذه المقالة هي ببساطة نتيجة الفضول والاهتمام الخمول ، لا يوجد شيء منها في الممارسة العملية ، ولا يوجد أي شيء للصق النسخ للمهام العملية. ولكن النتيجة ليست متوقعة تماما. الإنترنت مليء بأوصاف تشغيل الشبكات التي يخبر بها المؤلفون بشكل جميل ومع الصور كيف تحدد الشبكات البدائية - الزوايا ، والدوائر ، والشعيرات ، والذيول ، وما إلى ذلك ، ثم يتم البحث عن التقسيم / التصنيف. يتم الفوز بالعديد من المسابقات باستخدام الأوزان من الشبكات الكبيرة والعريضة الأخرى. من المثير للاهتمام أن نفهم ونرى كيف وما هي البدائل التي تبنيها الشبكة.
سنجري دراسة صغيرة وننظر في الخيارات - يتم تقديم منطق المؤلف ورمزه ، ويمكنك التحقق من / استكمال / تغيير كل شيء بنفسك.
انتهت المنافسة البحثية البحرية kaggle في الآونة الأخيرة. اقترحت إيرباص تحليل صور الأقمار الصناعية للبحر مع وبدون سفن. في إجمالي 192555 صور 768 × 768 × 3 - تبلغ 340 720 680 960 بايت إذا كان uint8 وأربعة أضعاف إذا float32 (بالمناسبة float32 أسرع من float64 ، وصول أقل للذاكرة) وفي 15606 صورة تحتاج إلى العثور على سفن. كالعادة ، اتخذت جميع الأماكن الهامة من قبل الأشخاص المشاركين في ODS (ods.ai) ، وهو أمر طبيعي ومتوقع ، وآمل أن نتمكن قريباً من دراسة مجموعة الأفكار ورمز الفائزين والفائزين بالجوائز.
سننظر في مشكلة مماثلة ، لكننا سنعمل على تبسيطها بشكل كبير - لنأخذ البحر np.random.sample () * 0.5 ، ولا نحتاج إلى الأمواج والرياح والسواحل وغيرها من الأنماط والوجوه الخفية. لنجعل صورة البحر عشوائية حقًا في نطاق RGB من 0.0 إلى 0.5. سنقوم بتلوين الأوعية في نفس اللون وتمييزها عن البحر ، وسنضعها في النطاق من 0.5 إلى 1.0 ، وستكون جميعها بنفس الشكل - علامات القطع ذات الأحجام والتوجهات المختلفة.

خذ نسخة شائعة جدًا من الشبكة (يمكنك أن تأخذ شبكتك المفضلة) وسنفعل جميع التجارب معها.
بعد ذلك ، سنقوم بتغيير معلمات الصورة ، وإنشاء التداخل وبناء الفرضيات - لذلك نحن نسلط الضوء على الميزات الرئيسية التي تعثر عليها الشبكة من علامات القطع. ربما يستخلص القارئ استنتاجاته ويدحض المؤلف.
نقوم بتحميل المكتبات ، ونحدد أحجام مجموعة من الصورimport numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm_notebook, tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau from keras.models import load_model from keras.optimizers import Adam from keras.layers import Input, Conv2D, Conv2DTranspose, MaxPooling2D, concatenate, Dropout from keras.losses import binary_crossentropy import tensorflow as tf import keras as keras from keras import backend as K from tqdm import tqdm_notebook w_size = 256 train_num = 8192 train_x = np.zeros((train_num, w_size, w_size,3), dtype='float32') train_y = np.zeros((train_num, w_size, w_size,1), dtype='float32') img_l = np.random.sample((w_size, w_size, 3))*0.5 img_h = np.random.sample((w_size, w_size, 3))*0.5 + 0.5 radius_min = 10 radius_max = 30
تحديد وظائف الخسارة والدقة def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
نحن نستخدم المقياس الكلاسيكي في تجزئة الصورة ، وهناك الكثير من المقالات ، والكود مع التعليقات والنص حول المقياس المحدد ، في نفس kaggle هناك الكثير من الخيارات مع التعليقات والشرح. سوف نتوقع قناع البكسل - هذا هو "البحر" أو "القارب" وتقييم حقيقة أو زيف التنبؤ. أي الخيارات الأربعة التالية ممكنة - لقد توقعنا بشكل صحيح أن البيكسل هو "بحر" ، وتوقعنا بشكل صحيح أن البيكسل هي "سفينة" أو أخطأ في توقع "بحر" أو "سفينة". وهكذا ، بالنسبة لجميع الصور وجميع وحدات البكسل ، نقدر عدد الخيارات الأربعة ونحسب النتيجة - سيكون ذلك نتيجة الشبكة. وكلما كانت التنبؤات أقل خطأ والأكثر صحة ، كانت النتيجة أكثر دقة وأفضل شبكة.
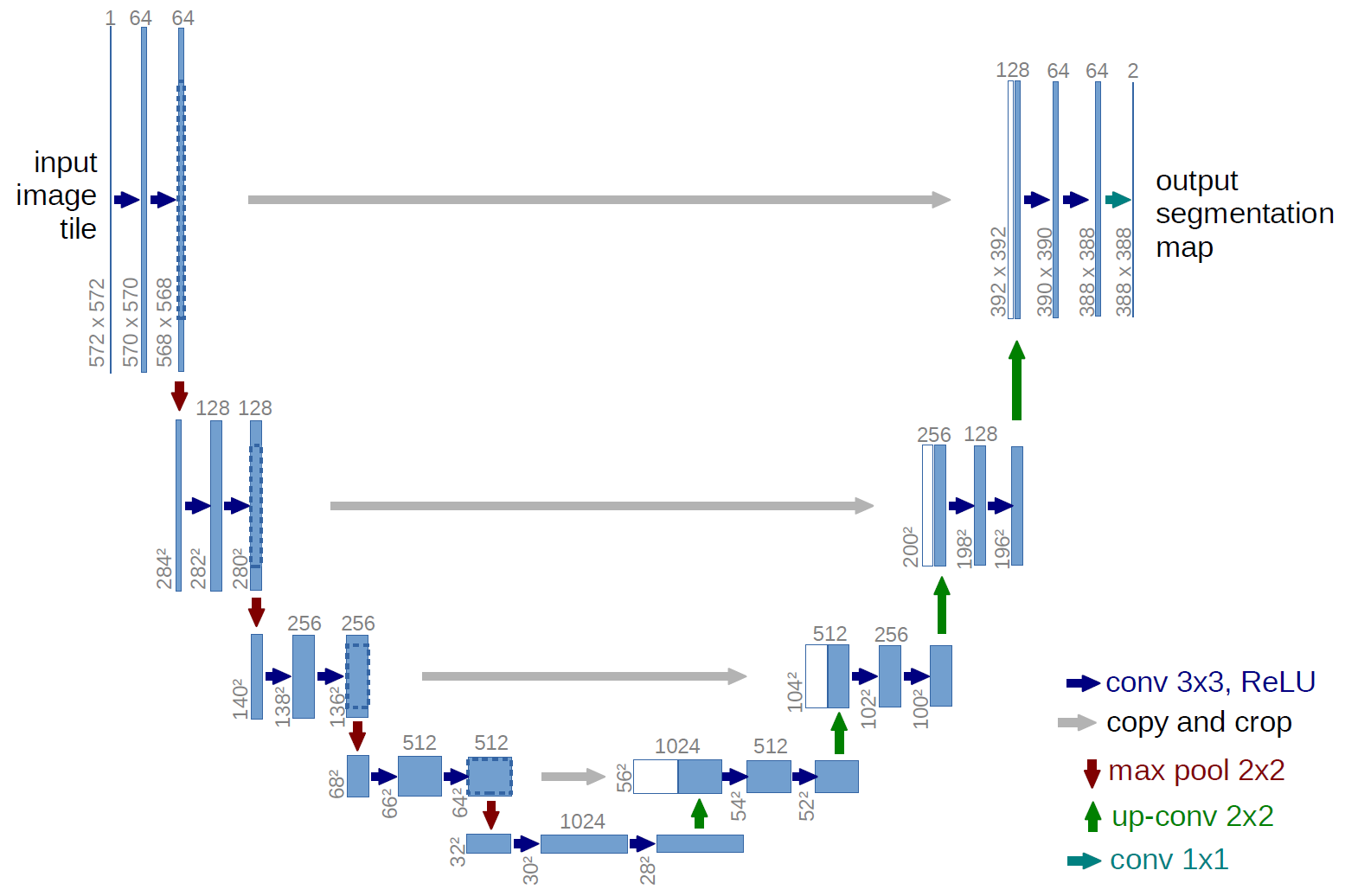
ولأغراض البحث ، دعنا نأخذ شبكة u المدروسة جيدًا ، وهي شبكة ممتازة لتجزئة الصور. تعتبر الشبكة شائعة جدًا في مثل هذه المسابقات ، وهناك العديد من الأوصاف ، التفاصيل الدقيقة للتطبيق ، إلخ. تم اختيار متغير من شبكة U-net الكلاسيكية ، وبطبيعة الحال ، كان من الممكن ترقيته ، وإضافة كتل متبقية ، إلخ. ولكن "لا يمكنك احتضان ضخامة" وإجراء جميع التجارب والاختبارات في وقت واحد. تقوم U-net بإجراء عملية بسيطة للغاية باستخدام الصور - فهي تقلل من حجم الصورة مع بعض التحويلات خطوة بخطوة ثم تحاول استعادة القناع من الصورة المضغوطة. أي يصل حجم الصورة في حالتنا إلى 32 × 32 ، ثم نحاول استعادة القناع باستخدام البيانات من جميع الضغطات السابقة.
في الصورة ، مخطط U-net هو من المقالة الأصلية ، لكننا أعيدنا صياغته قليلاً ، لكن يبقى جوهره كما هو - نضغط الصورة → نوسع إلى قناع.
فقط U- صافي def build_model(input_layer, start_neurons): conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(input_layer) conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(conv1) pool1 = MaxPooling2D((2, 2))(conv1) pool1 = Dropout(0.25)(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(conv2) pool2 = MaxPooling2D((2, 2))(conv2) pool2 = Dropout(0.5)(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(conv3) pool3 = MaxPooling2D((2, 2))(conv3) pool3 = Dropout(0.5)(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(conv4) pool4 = MaxPooling2D((2, 2))(conv4) pool4 = Dropout(0.5)(pool4)
التجربة الأولى. أسهل
تم اختيار الإصدار الأول من تجربتنا ليكون البساطة بسيطة جدًا - البحر أخف ، والسفن أغمق. كل شيء بسيط للغاية وواضح ، نحن نفترض أن الشبكة سوف تجد السفن / الحذف دون مشاكل وبأية دقة. تولد وظيفة next_pair زوجًا من الصورة / القناع ، يتم فيه تحديد المكان والحجم وزاوية الدوران بشكل عشوائي. علاوة على ذلك ، سيتم إجراء جميع التغييرات على هذه الوظيفة - تغيير في اللون ، الشكل ، التداخل ، إلخ. ولكن الآن أصبح الخيار الأسهل هو اختبار فرضية القوارب المظلمة على خلفية فاتحة.
def next_pair(): p = np.random.sample() - 0.5
نحن نولد القطار كله ونرى ما حدث. يبدو مثل القوارب في البحر ولا أكثر. كل شيء واضح بشكل واضح وواضح ومفهوم. الموقع عشوائي وليس هناك سوى قطع ناقص واحد في كل صورة.
for k in range(train_num):
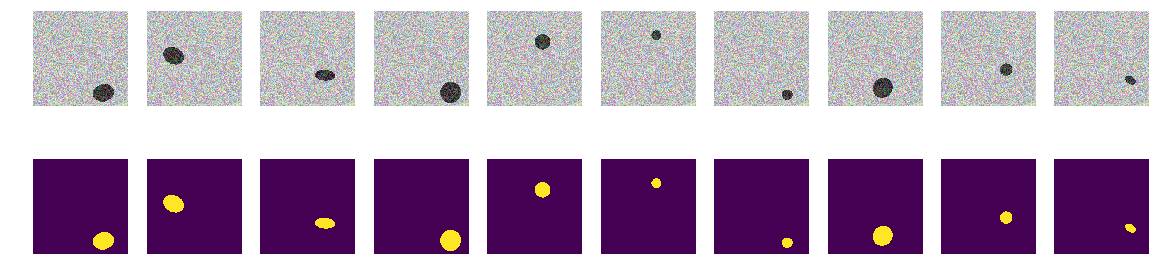
ليس هناك شك في أن الشبكة سوف تتعلم بنجاح وستجد الحذف. ولكن دعونا نختبر فرضيتنا المتمثلة في أن الشبكة مدربة للعثور على القطع / السفن وفي نفس الوقت بدقة عالية.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.save_weights('./keras.weights') while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.2272 - my_iou_metric: 0.7325 - val_loss: 0.0063 - val_my_iou_metric: 1.0000
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0090 - my_iou_metric: 1.0000 - val_loss: 0.0045 - val_my_iou_metric: 1.0000
تعثر الشبكة على علامات الحذف بنجاح. ولكن لم يثبت على الإطلاق أنها تبحث عن علامات استقصائية في فهم الرجل ، كمنطقة تحدها معادلة القطع الناقص ومليئة بمحتوى مختلف عن الخلفية ، لا يوجد يقين من وجود أوزان شبكية مماثلة لمعاملات معادلة القطع الناقص التربيعية. ومن الواضح أن سطوع القطع الناقص أقل من سطوع الخلفية وليس سراً أو لغزًا - نفترض أننا فحصنا الكود. دعونا إصلاح وجه واضح ، وجعل الخلفية ولون القطع الناقص عشوائي أيضا.
الخيار الثاني
الآن نفس الحذف موجودة في نفس البحر ، ولكن لون البحر ، وبالتالي ، يتم اختيار القارب بشكل عشوائي. إذا كان البحر أغمق ، فستكون السفينة أخف وزناً والعكس صحيح. أي من خلال سطوع مجموعة النقاط ، من المستحيل تحديد ما إذا كانت خارج القطع الناقص ، أي البحر أو تلك نقاط داخل القطع الناقص. مرة أخرى ، نقوم باختبار فرضيتنا المتمثلة في أن الشبكة ستعثر على علامات تمييز بغض النظر عن اللون.
def next_pair(): p = np.random.sample() - 0.5
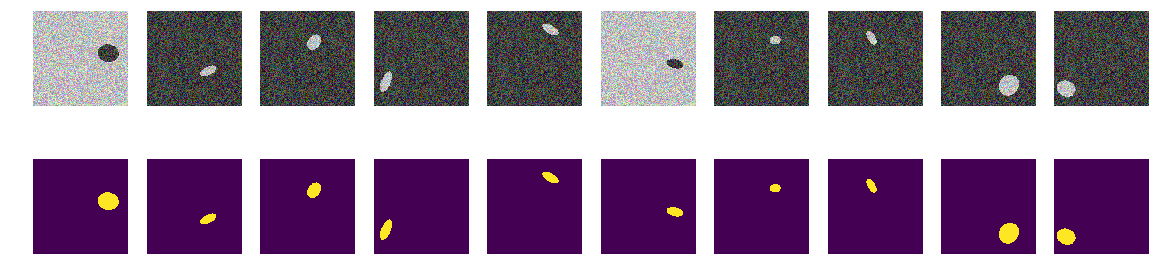
الآن ، بالبكسل ومحيطه ، من المستحيل تحديد الخلفية أو القطع الناقص. نحن أيضا إنشاء الصور والأقنعة وننظر إلى أول 10 على الشاشة.
أقنعة البناء for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.4652 - my_iou_metric: 0.5071 - val_loss: 0.0439 - val_my_iou_metric: 0.9005
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.1418 - my_iou_metric: 0.8378 - val_loss: 0.0377 - val_my_iou_metric: 0.9206تتكيف الشبكة بسهولة وتجد كل علامات القطع. ولكن هنا ، هناك عيب في التنفيذ ، وكل شيء واضح - أصغر من المنطقتين في الصورة هو القطع الناقص ، خلفية أخرى. ربما تكون هذه فرضية زائفة ، ولكن مع ذلك لا يزال حلها ، أضف مضلعًا آخر للصورة بنفس لون القطع الناقص.
الخيار الثالث
في كل صورة ، نختار لون البحر بشكل عشوائي من الخيارين ونضيف شكل بيضاويًا ومستطيلًا ، وكلاهما يختلف عن لون البحر. يتحول إلى نفس "البحر" ، وأيضًا "قارب" مطلي ، ولكن في نفس الصورة نضيف مستطيلًا بنفس لون "القارب" وأيضًا بحجم محدد بشكل عشوائي. أصبح افتراضنا أكثر تعقيدًا ، حيث يوجد في الصورة كيانان متطابقان اللون ، لكننا نفترض أن الشبكة ستظل تتعلم كيفية اختيار الكائن الصحيح.
برنامج لرسم الحذف والمستطيلات كما كان من قبل ، نحسب الصور والأقنعة وننظر إلى أول 10 أزواج.
بناء قناع الصور الحذف والمستطيلات for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 57s 8ms/step - loss: 0.7557 - my_iou_metric: 0.0937 - val_loss: 0.2510 - val_my_iou_metric: 0.4580
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.0719 - my_iou_metric: 0.8507 - val_loss: 0.0183 - val_my_iou_metric: 0.9812لا يمكن الخلط بين مستطيلات الشبكة وتأكيد فرضيتنا. استنادا إلى الأمثلة والمناقشات ، كان لدى كل شخص في مسابقة إيرباص سفن واحدة ، وكانت العديد من السفن في مكان قريب تمامًا. القطع الناقص من المستطيل - على سبيل المثال السفينة من المنزل على الشاطئ ، تتميز الشبكة ، على الرغم من أن المضلعات هي نفس لون القطع الناقصة. إنها ليست مسألة لون ، لأن كل من القطع الناقص والمستطيل يتم رسمهما بشكل عشوائي.
الخيار الرابع
ربما تتميز الشبكة عن طريق المستطيلات - صحيح ، وتشويهها. أي تعثر الشبكة بسهولة على المساحات المغلقة بغض النظر عن الشكل وتتجاهل المنطقة المستطيلة. هذه هي فرضية المؤلف - سنقوم بفحصها ، والتي لن نضيف إليها مستطيلات ، بل مضلعات رباعية الزوايا ذات شكل اعتباطي. ومرة أخرى ، فإن فرضيتنا هي أن الشبكة تميز القطع الناقص عن مضلع رباعي الزوايا من نفس اللون.
يمكنك بالطبع الدخول في الدواخل الموجودة في الشبكة وهناك إلقاء نظرة على الطبقات وتحليل معنى الأوزان والتحولات. يهتم المؤلف بالسلوك الناتج للشبكة ، وسوف يستند الحكم إلى نتيجة العمل ، على الرغم من أنه من المثير للاهتمام دائمًا النظر إلى الداخل.
إجراء تغييرات على توليد الصور def next_pair(): p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min) p1 = np.rint(np.random.sample()*(w_size-radius_max)) p2 = np.rint(np.random.sample()*(w_size-radius_max)) p3 = np.rint(np.random.sample()*2.*radius_min - radius_min) p4 = np.rint(np.random.sample()*2.*radius_min - radius_min) p5 = np.rint(np.random.sample()*2.*radius_min - radius_min) p6 = np.rint(np.random.sample()*2.*radius_min - radius_min) p7 = np.rint(np.random.sample()*2.*radius_min - radius_min) p8 = np.rint(np.random.sample()*2.*radius_min - radius_min) poly = np.array(( (p1, p2), (p1+p3, p2+p4+p0), (p1+p5+p0, p2+p6+p0), (p1+p7+p0, p2+p8), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc = list(set(rr) & set(rr_p)) if len(in_sc) > 0: if np.mean(rr_p) > np.mean(in_sc): poly += np.max(in_sc) - np.min(in_sc) else: poly -= np.max(in_sc) - np.min(in_sc) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img = img_l.copy() img[rr, cc] = img_h[rr, cc] img[rr_p, cc_p] = img_h[rr_p, cc_p] else: img = img_h.copy() img[rr, cc] = img_l[rr, cc] img[rr_p, cc_p] = img_l[rr_p, cc_p] msk = np.zeros((w_size, w_size, 1), dtype='float32') msk[rr, cc] = 1. return img, msk
نحسب الصور والأقنعة وننظر إلى أول 10 أزواج.
نبني أقنعة الصور الحذف والمضلعات for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

نطلق شبكتنا. واسمحوا لي أن أذكرك أنه هو نفسه بالنسبة لجميع الخيارات.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.6815 - my_iou_metric: 0.2168 - val_loss: 0.2078 - val_my_iou_metric: 0.4983
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.1470 - my_iou_metric: 0.6396 - val_loss: 0.1046 - val_my_iou_metric: 0.7784
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0642 - my_iou_metric: 0.8586 - val_loss: 0.0403 - val_my_iou_metric: 0.9354
تم تأكيد الفرضية ، والمضلعات والقطع الناقص يمكن تمييزها بسهولة. سوف يلاحظ القارئ اليقظ هنا - بطبيعة الحال مختلف ، سؤال هراء ، أي الذكاء الاصطناعى العادي يمكن أن يميز منحنى من الدرجة الثانية من سطر الأول. أي تحدد الشبكة بسهولة وجود حد في شكل منحنى من الدرجة الثانية. نحن لن نجادل ، واستبدال البيضاوي مع مسدس والتحقق.
التجربة الخامسة ، الأصعب
لا توجد منحنيات ، فقط الوجوه الملساء لسباعي الأضلاع المائلة والمدارة والمضلعات التعسفية الرباعية الزوايا. نعرض في الوظيفة تغييرات مولد الصورة / القناع - فقط إسقاطات heptagons العادية والمضلعات رباعية الزوايا من نفس اللون.
المراجعة النهائية لوظيفة توليد الصور def next_pair(_n = 7): p = np.random.sample() - 0.5 c_x = np.random.sample()*(w_size-2*radius_max) + radius_max c_y = np.random.sample()*(w_size-2*radius_max) + radius_max radius = np.random.sample()*(radius_max-radius_min) + radius_min d = np.random.sample()*0.5 + 1 a_deg = np.random.sample()*360 a_rad = np.deg2rad(a_deg) poly = []
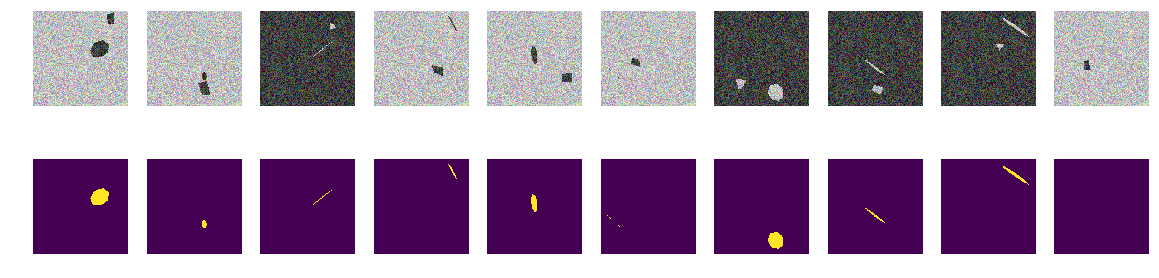
كما كان من قبل ، نبني المصفوفات وننظر إلى أول 10.
أقنعة البناء for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 54s 7ms/step - loss: 0.5005 - my_iou_metric: 0.1296 - val_loss: 0.1692 - val_my_iou_metric: 0.3722
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.1287 - my_iou_metric: 0.4522 - val_loss: 0.0449 - val_my_iou_metric: 0.6833
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0759 - my_iou_metric: 0.5985 - val_loss: 0.0397 - val_my_iou_metric: 0.7215
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0455 - my_iou_metric: 0.6936 - val_loss: 0.0297 - val_my_iou_metric: 0.7304
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0432 - my_iou_metric: 0.7053 - val_loss: 0.0215 - val_my_iou_metric: 0.7846
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0327 - my_iou_metric: 0.7417 - val_loss: 0.0171 - val_my_iou_metric: 0.7970
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0265 - my_iou_metric: 0.7679 - val_loss: 0.0138 - val_my_iou_metric: 0.8280ملخص
كما ترون ، تميز الشبكة بين إسقاطات heptagons العادية والمضلعات الرباعية الزوايا بدقة 0.828 في مجموعة الاختبار. تم إيقاف التدريب على الشبكة بقيمة تعسفية قدرها 0.75 وعلى الأرجح ينبغي أن تكون الدقة أفضل بكثير. إذا انطلقنا من الأطروحة التي تفيد بأن الشبكة تجد بدائية وأن مجموعاتها تحدد الكائن ، ففي حالتنا هناك منطقتان بمتوسط مختلف عن الخلفية ، لا توجد بدائل في فهم الإنسان. لا توجد خطوط واضحة ذات لون واحد ، ولا توجد زوايا ، على التوالي ، فقط المناطق ذات الحدود المتشابهة للغاية. حتى إذا كنت تقوم ببناء خطوط ، فإن كلا الكائنين في الصورة مبنيان من نفس العناصر الأولية.
سؤال للخبراء - ما الذي تعتبره الشبكة كعلامة تميز "القوارب" من "التدخل"؟ من الواضح أن هذا ليس لون أو شكل حدود القوارب. بالطبع ، يمكننا أن نستمر في دراسة هذا البناء المجرد للسفن "البحرية" / "السفن" ، لسنا أكاديمية العلوم ويمكننا إجراء البحوث بدافع الفضول فقط. يمكننا تغيير heptagons إلى ثماني أو ملء الصورة بخمسة وستة زوايا منتظمة ومعرفة ما إذا كانت شبكتهم تميز أم لا. أترك هذا للقراء - على الرغم من أنني تساءلت أيضًا عما إذا كان يمكن للشبكة حساب عدد زوايا المضلع وترتيب ، ليس للاختبار ، المضلعات المنتظمة في الصورة ، ولكن توقعاتهم العشوائية.
هناك خصائص أخرى لا تقل إثارة للاهتمام لهذه القوارب ، وهذه التجارب مفيدة لأننا نحن أنفسنا نضع جميع الخصائص الاحتمالية للمجموعة المدروسة ، والسلوك غير المتوقع للشبكات المدروسة جيدًا سيضيف المعرفة ويجلب فوائد.
تم تحديد الخلفية بشكل عشوائي ، ويتم اختيار اللون بشكل عشوائي ، ويتم تحديد موقع القارب / القطع الناقص بشكل عشوائي. لا توجد خطوط في الصور ، هناك مناطق ذات خصائص مختلفة ، لكن لا توجد خطوط أحادية اللون! في هذه الحالة ، بالطبع ، هناك عمليات تبسيط ويمكن زيادة تعقيد المهمة - على سبيل المثال ، اختيار ألوان مثل 0.0 ... 0.9 و 0.1 ... 1.0 - ولكن بالنسبة للشبكة ، لا يوجد فرق. يمكن للشبكة العثور على أنماط مختلفة عن تلك التي يراها الشخص ويجدها.
إذا كان أحد القراء مهتمًا ، فيمكنك متابعة البحث والتقاط الشبكات ، وإذا لم ينجح الأمر أو لم يكن واضحًا ، أو إذا ظهر فكر جديد وجيد ومثير للإعجاب بجماله ، فيمكنك دائمًا مشاركتنا معنا أو سؤال الأساتذة (والجدات أيضًا) وطلب المساعدة المؤهلة في مجتمع المواد المستنفدة للأوزون.