عبقري وكاتب رياضي غامض يعززان حل مشكلة التقليب

تم الاعتراف بالأدلة الجديدة ، التي ألفها كاتب الخيال العلمي الأسترالي جريج إيغان ، وإثبات عام 2011 ، الذي تم نشره بشكل مجهول على الإنترنت ، على أنها اختراقات مهمة في دراسة اللغز الذي يبحث عنه علماء الرياضيات منذ 25 عامًا.

في 16 سبتمبر 2011 ، نشر أحد المعجبين بالأنيم سؤال الرياضيات 4chan على سلسلة عبادة " حزن Haruhi Suzumiya " في المنتدى. تم عرض الموسم الأول من العرض ، حيث كانت هناك رحلات زمنية ، بترتيب مختلف عن الترتيب الزمني ، وخلال العرض والإصدار اللاحقين على قرص DVD ، تم تغيير ترتيب الحلقات مرة أخرى. على الإنترنت ، جادل المعجبون بترتيب مشاهدة المسلسل على نحو أفضل ، وسأل مؤلف السؤال: إذا كان الجمهور يرغب في مشاهدة المسلسل في جميع الطلبات المحتملة ، فكم عدد الحلقات التي ستكون على قائمة أقصر؟ [ يشير إلى قائمة يمكنك أن تجد فيها أي سلسلة من الحلقات / تقريبا. perev. ]

في أقل من ساعة ، قدم أحد المؤلفين المجهولين إجابة على السؤال - ليس حلاً كاملاً ، بل حد أدنى لعدد الحلقات المطلوب. من منطقه ، المطبق على أي عدد من الحلقات ، تبع ذلك أنه بالنسبة للموسم الأول من Haruhi ، والذي يتكون من 14 حلقة ، سيتعين على الجمهور مشاهدة ما لا يقل عن 93،884،313،611 حلقة على التوالي لدراسة جميع التباديل الممكنة. وكتب مؤلف الرد "تفحص الدليل على العيوب التي ربما تكون قد فاتني".

لمدة سبع سنوات ، ذهب الدليل دون أن يلاحظه أحد في المجتمع الرياضي - اتضح أنه في تلك اللحظة لاحظه عالم رياضيات محترف واحد فقط ، ولم يدرسه جيدًا بما فيه الكفاية. ومع ذلك ، فجأة في الشهر الماضي ، أثبت كاتب الخيال العلمي الأسترالي جريج إيغان حدًا أعلى جديدًا لعدد الحلقات المطلوبة. أعاد اكتشاف إيجان الاهتمام بالمهمة ولفت الانتباه إلى السجل المتعلق بالحد الأدنى لعام 2011. يعتبر كل من هذه الأدلة الآن طفرات كبيرة في دراسة اللغز الذي ظل علماء الرياضيات يبحثون عنه منذ 25 عامًا على الأقل.

قام علماء الرياضيات بالتحقق بسرعة من الحد العلوي من Egan ، والذي ينطبق ، مثل الحد الأدنى ، على متواليات من أي طول. ثم أكد روبن هيوستن ، وهو عالم رياضيات في Kiln ، وهي شركة لتصور البيانات ، وجاي بانتون من جامعة ماركويت في ميلووكي ، عمل مؤلف مجهول مع 4chan. وقال بانتون: "بذلت جهود كثيرة للتحقق من صحة هذه الفرضية" ، حيث لم يتم التعبير بوضوح عن الأفكار الرئيسية للدليل.

والآن ، قام كل من هيوستن وبانتون ، مع فينس فاتر من جامعة فلوريدا ، بكتابة عمل رسمي . في ذلك ، أشاروا إلى المؤلف الأول بأنه "ملصق 4chan مجهول".

وقال هيوستن: "الشيء الغريب هو أن هذا الدليل الأنيق للغاية لحقيقة غير معروفة سابقًا ظهر في مثل هذا المكان غير المحتمل".

مدن التباديل

إذا كانت السلسلة تحتوي على ثلاث حلقات فقط ، فهناك ست طرق ممكنة لمشاهدتها: 123 و 132 و 213 و 231 و 312 و 321. يمكن لصقها معًا ووضع قائمة من 18 حلقة ، بما في ذلك كل إصدار من الترتيب. ومع ذلك ، هناك أيضًا طريقة لصق أكثر فاعلية: 123121321. يسمى هذا التسلسل الذي يحتوي على جميع التباديل لمجموعة من الأحرف n باسم التقليب الفائق.

في عام 1993 ، اكتشف دانيال آشلوك وجانيت تيلوتسون أنه عند دراسة أقصر التباديل الفائقة لقيم مختلفة من n ، تبدأ الفصائل في الظهور بسرعة - نفس القيم المكتوبة في النموذج n! ، أي ضرب كل الأرقام من 1 إلى n (على سبيل المثال ، 4 ! = 4 * 3 * 2 * 1).

إذا كان هناك حلقة واحدة فقط في السلسلة ، فسيكون طول أقصر التقليب الفائق 1! (المعروف أيضا باسم الوحدة القديمة الجيدة). لسلسلة من حلقتين ، أقصر التقليب الفائق (121) يبلغ طوله 2! + 1! .. لمدة ثلاث حلقات (المثال أعلاه) ، الطول 3! + 2! + 1! ، ولأربع حلقات (123412314231243121342132413214321) ستكون 4! + 3! + 2! + 1! .. أصبحت قاعدة الفصائل مقبولة عمومًا (على الرغم من أنه لا يمكن لأحد إثبات أنها صحيحة لكل n) ، وقد أكد علماء الرياضيات لاحقًا على n = 5.

ثم في عام 2014 ، أعجب هيوستن علماء الرياضيات ، حيث أظهروا أنه بالنسبة إلى n = 6 ، توقفت القاعدة عن العمل. تتوقع القاعدة أن الأمر سيستغرق 873 حلقة لمشاهدة ستة حلقات بكل طريقة ممكنة ، ولكن هيوستن وجدت طريقة للقيام بذلك في 872. وبما أن هناك طريقة بسيطة لتحويل التقليب الفائق القصير للأحرف n إلى تقليب فائق قصير لأحرف n + 1 ، فإن مثال هيوستن يعني أن القاعدة الفصائل لا تعمل لجميع ن> 6.

يحول بناء هيوستن مهمة التقليب الفائق إلى مشكلة البائع المتجول الشهير ، والتي تبحث عن أقصر طريق في عدة مدن. على وجه التحديد ، ترتبط التباديل الفائق بمشكلة البائع "غير المتماثلة" ، حيث يكون لكل مسار بين مدينتين سعره الخاص (وليس بالضرورة هو نفسه في كلا الاتجاهين) ، والهدف هو العثور على أرخص طريق عبر جميع المدن.

من السهل فهم هذا التحول: تخيل أن كل تقليب هو مدينة ، وتخيل المسار من كل التقليب إلى كل التقليب الآخر. في مشكلة التقليب الفائق ، نحتاج إلى أقصر تسلسل من الأرقام التي توجد فيها جميع التباديل ، لذلك هدفنا هو المرور عبر جميع التباديل وذلك لإضافة أكبر عدد ممكن من الأرقام إلى التقليب الأولي. نعلن أن تكلفة كل مسار هي ببساطة عدد الأرقام التي نحتاج إلى إرفاقها في نهاية التقليب الأول للحصول على الثاني. في المثال مع n = 3 ، يكلف المسار من 231 إلى 312 دولارًا واحدًا ، حيث نحتاج إلى إضافة 2 فقط إلى نهاية 231 للحصول على 312 ، والمسار من 231 إلى 132 يكلف 2 دولارًا ، نظرًا لأننا بحاجة إلى إضافة 32. في هذه الصيغة ، أرخص طريقة من خلال جميع المدن تتوافق مباشرة مع أقصر التقليب.



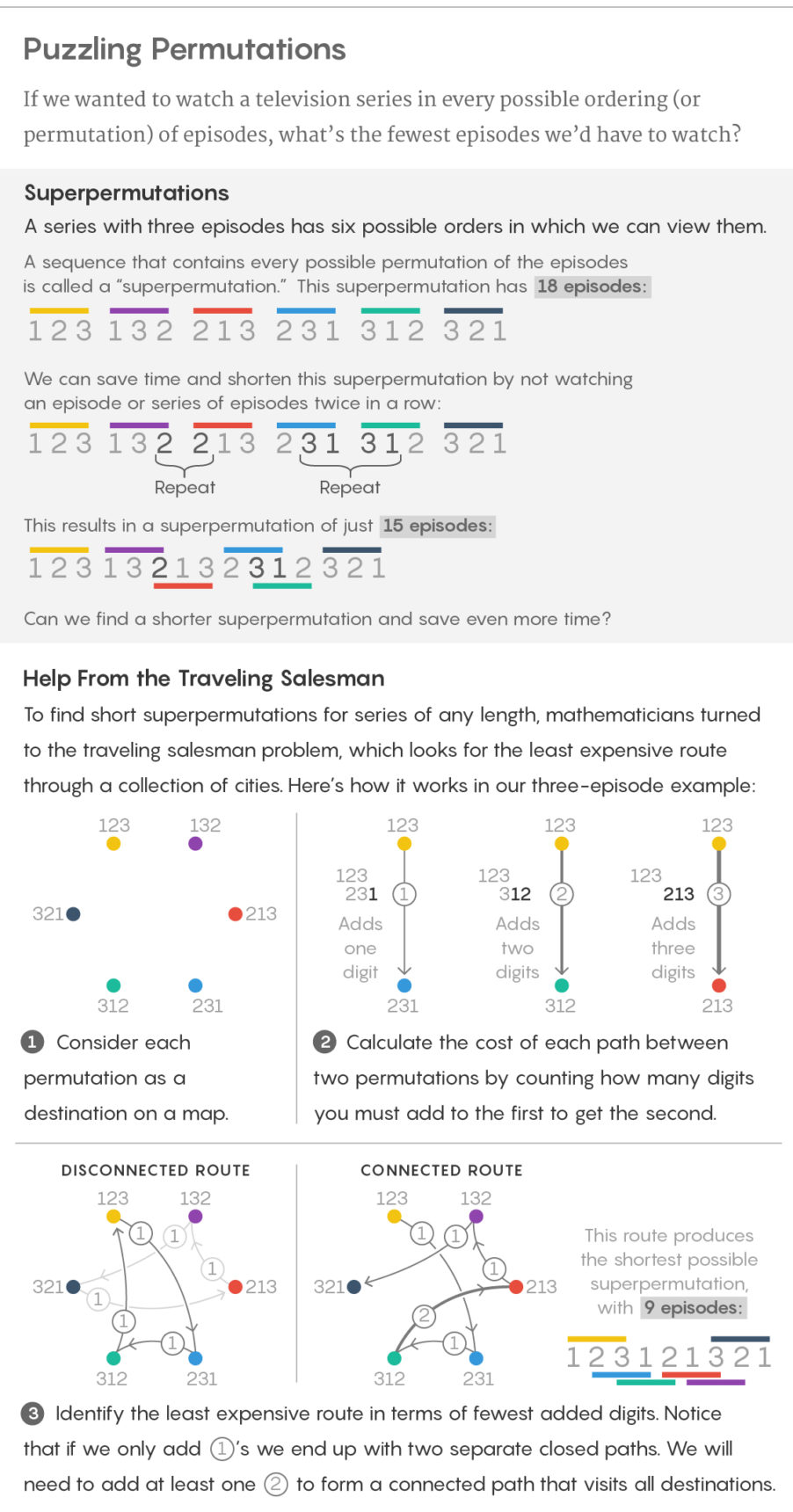
مثل هذا التحول يعني أن هيوستن يمكن أن توجه جميع قدرات الخوارزميات لحل مشكلة البائع المتجول إلى مشكلة التقليب الفائق. تُعرف هذه المشكلة بانتمائها إلى فئة المعقدات NP ، مما يعني عدم وجود خوارزمية فعالة يمكنها حلها في الحالة العامة. ومع ذلك ، هناك خوارزميات يمكنها حل بعض أصناف المشكلة بشكل فعال ، ويمكن للخوارزميات الأخرى إنتاج حلول تقريبية جيدة. استخدم هيوستن واحدًا من الأخير لإصدار التقليب الفائق المكون من 872 رقمًا.

نظرًا لأنه قدم حلاً تقريبيًا فقط ، فقد لا يكون هذا هو الحل الأكثر مثالية. وقال بانتون إن علماء الرياضيات يقومون الآن بإجراء بحث حسابي ضخم لأقصر تقليب من 6 أحرف. وقال "نحن نعلم أن عمليات البحث لدينا ستنتهي في وقت محدد ، لكننا لا نعرف ما إذا كان سيستغرق أسبوعًا أو مليون عام". "لا يوجد شريط التقدم".

ترتيب خاطئ

في الوقت الذي ظهر فيه عمل هيوستن ، كان موقع مجهول على قناة 4chan في ركن الإنترنت لمدة ثلاث سنوات تقريبًا. لاحظ عالم الرياضيات ، ناثانييل جونستون من جامعة ماونت إليسون ، نسخة من هذا المنشور في موقع آخر بعد بضعة أيام من ظهور هذا المنشور - وليس لأنه كان محبًا لأنيمي ، ولكن لأنه أدخل طلبات متعددة في Google ، المرتبطة التباديل الفائق.

قام جونستون بقراءة الدليل وبدا أنه موثوق به ، لكنه لم يضيع طاقته في فحص شامل. في ذلك الوقت ، اعتقد علماء الرياضيات أن الصيغة الموصوفة للتباديل الفائق كانت على الأرجح صحيحة ، وعندما تعتقد أنك تعرف الإجابة الدقيقة على سؤال ما ، فأنت غير مهتم بالحد الأدنى للتقدير. بمعنى آخر ، كانت حلقات المسلسل حول التباديل الفائق تسير وفق الترتيب الخاطئ.

بعد ذلك ، ذكر جونستون الحد الأدنى على زوج من المواقع الإلكترونية ، لكن "لا أعتقد أن أي شخص قد أولى اهتمامًا خاصًا بهذا الأمر" ، على حد قوله.

ثم ، في 26 سبتمبر 2018 ، قام عالم الرياضيات جون بايز من جامعة كاليفورنيا في ريفرسايد بتغريد منشور عن اكتشاف هيوستن في عام 2014 ، كجزء من سلسلة من التغريدات حول أنماط رياضية واضحة تتوقف عن العمل.

ملاحظة perev.: لم يكن هناك مثل هذه السلسلة الكبيرة من التغريدات ، ثلاثة فقط. الاثنان الآخران مثيران للاهتمام في حد ذاته ، رغم أنهما لا يرتبطان بهذا المقال. واحد يقول أن 6 هي المسافة الأكثر شعبية بين اثنين من الأعداد الأولية المجاورة لجميع الأعداد الأولية أقل من 172700000000،000،000،000،000،000،000،000،000،000 ، ثم هذا النمط توقف فجأة عن العمل! يوضح الثاني الاتصال التالي من التكاملات ، الدوال المثلثية والرقم π



لكن فقط لـ n <9.8 × 10 ⁴² !

لفتت تغريدة اهتمام إيغان ، الذي درس الرياضيات قبل عدة عقود ، قبل أن يبدأ حياته المهنية ككاتب خيال علمي معترف به (كانت أول قصة ناجحة له ، حظاً سعيداً ، تسمى "مدينة التباديل"). "لم أتوقف أبدًا عن الاهتمام بالرياضيات" ، كتب إيجان في البريد.

تساءل إيجان عما إذا كان من الممكن إنشاء تقليب فائق حتى أقصر من ذلك في هيوستن. لقد اندمج في دراسة الأدبيات المتعلقة بكيفية إنشاء اختصارات في شبكات التباديل ، وبعد بضعة أسابيع وجد ما يحتاج إليه. في بضعة أيام ، استنتج حدًا أعلى جديدًا على طول أقصر التقليب الفائق للأحرف n: n! + (ن - 1)! + (ن - 2)! + (ن - 3)! + n - 3. إنها تشبه الصيغة الحزبية التي استُبعد منها العديد من الأعضاء.

"لقد كسر تماما الحد العلوي السابق" ، وقال هيوستن.

كان الحد الأدنى لمؤلف المشاركة في 4chan قريبًا بشكل مغر من الحد الأعلى الجديد: n! + (ن - 1)! + (ن - 2)! + n - 3. بعد نشر النتيجة ، ذكّر إغان جونستون علماء الرياضيات بإثبات مؤلف مجهول ، وسرعان ما أثبتت هيوستن وبانتون صحتها. كما هو الحال في عمل هيوستن ، تتناسب الحدود الدنيا والعليا الجديدة مع التباينات الفائقة من وجهة نظر مشكلة البائع المتجول: يظهر الحد الأدنى أن المسار عبر جميع المدن يجب أن يمر ببعض الحد الأدنى لعدد المسارات التي تزيد قيمتها عن دولار واحد ، والحد الأعلى يخلق مسارًا خاصًا لكل n ، باستخدام المركبات فقط بقيمة 1 دولار و 2 دولار.

الآن ، يحاول الباحثون الجمع بين الحدود العليا والسفلى ، وإيجاد صيغة واحدة تحل مشكلة التقليب الفائق. "ربما ، في النهاية ، سيظل الناس يحلون هذا اللغز" ، كما توقع بايز. "الآن كل شيء يبدو جيدا."

بالنسبة لمحبي Haruhi ، يقدم حل Egan إرشادات دقيقة حول كيفية عرض جميع الخيارات الممكنة للموسم الأول باستخدام إجمالي 93،924،230،411. يمكنك البدء في المشاهدة اليوم ، أو يمكنك الانتظار حتى يتمكن علماء الرياضيات من خفض هذا الرقم. يثبت الحد الأدنى من مؤلف مجهول أن هذا التخفيض لن ينقذهم أكثر من 40 مليون حلقة - ومع ذلك ، هذا يكفي لبدء الاستعداد للموسم الثاني.