زمن التعلم: نظرية الانتظار

يصبح موضوع الكمون مع مرور الوقت مثيرًا للاهتمام في الأنظمة المختلفة في Yandex وليس فقط. يحدث هذا كما تظهر أي ضمانات خدمة في هذه الأنظمة. من الواضح أن الحقيقة هي أنه ليس من المهم فقط أن نعد ببعض الفرص للمستخدمين ، ولكن أيضًا لضمان استلامها بوقت استجابة معقول. تختلف "عقلانية" زمن الاستجابة ، بطبيعة الحال ، اختلافًا كبيرًا في الأنظمة المختلفة ، ولكن المبادئ الأساسية التي يتجلى بها زمن الانتقال في جميع الأنظمة شائعة ، ويمكن اعتبارها بمعزل عن الخصائص المحددة.

اسمي سيرجي تريفونوف ، أعمل في فريق Real-Time Map Reduce في ياندكس. نحن نعمل على تطوير نظام أساسي لمعالجة تدفق البيانات في الوقت الفعلي مع أوقات الاستجابة الثانية والثانية. النظام الأساسي متاح للمستخدمين الداخليين ويسمح لهم بتنفيذ كود التطبيق على تدفقات البيانات الواردة باستمرار. سأحاول تقديم نظرة عامة مختصرة على المفاهيم الأساسية للبشرية حول موضوع تحليل الكمون على مدى السنوات العشر الماضية ، وسنحاول الآن فهم ما يمكن تعلمه بالضبط عن الكمون باستخدام نظرية الطابور.

بدأت ظاهرة الكمون يتم التحقيق فيها بشكل منهجي ، حسب علمي ، فيما يتعلق بظهور أنظمة الانتظار - شبكات الاتصالات الهاتفية. بدأت نظرية الطوابير مع عمل إيه كيه إيرلانج في عام 1909 ، حيث أظهر أن توزيع بواسون ينطبق على حركة الهاتف العشوائية. طور إرلانج نظرية استخدمت منذ عقود لتصميم شبكات الهاتف. تسمح لنا النظرية بتحديد احتمال رفض الخدمة. بالنسبة لشبكات الهاتف ذات القنوات بتبديل الدارات ، حدث عطل إذا كانت جميع القنوات مشغولة ولا يمكن إجراء الاتصال. كان لا بد من السيطرة على احتمال هذا الحدث. كنت أرغب في الحصول على ضمان ، على سبيل المثال ، سيتم تقديم 95 ٪ من جميع المكالمات. تتيح صيغ Erlang تحديد عدد الخوادم اللازمة للوفاء بهذا الضمان إذا كانت مدة وعدد المكالمات معروفة. في الواقع ، هذه المهمة تتعلق فقط بضمانات الجودة ، واليوم لا يزال الناس يحلون مشكلات مماثلة. لكن الأنظمة أصبحت أكثر تعقيدًا. المشكلة الرئيسية لنظرية الطوابير هي أنها لا تدرس في معظم المؤسسات ، وقلة من الناس يفهمون السؤال خارج قائمة الانتظار M / M / 1 المعتادة (انظر الملاحظة أدناه ) ، ولكن من المعروف أن الحياة أكثر تعقيدًا بكثير من هذا النظام. لذلك ، أقترح ، تجاوز M / M / 1 ، انتقل مباشرة إلى الأكثر إثارة للاهتمام.

متوسط ​​القيم

إذا كنت لا تحاول اكتساب معرفة كاملة بتوزيع الاحتمالات في النظام ، ولكنك تركز على الأسئلة الأكثر بساطة ، يمكنك الحصول على نتائج مفيدة ومفيدة. الأكثر شهرة منهم ، بالطبع ، نظرية ليتل . إنه قابل للتطبيق على نظام به أي تدفق إدخال ، وجهاز داخلي بأي تعقيد وجدولة تعسفية بالداخل. الشرط الوحيد هو أن النظام يجب أن يكون مستقرًا: يجب أن يكون متوسط ​​أوقات الاستجابة وأطوال قائمة الانتظار ، ثم يتم توصيلها بتعبير بسيط

$$

$$L = \ lambda W$$

اين $$$L$ - متوسط ​​عدد الوقت للطلبات في الجزء المعتبر من النظام [pcs] ، $$$W$ - متوسط ​​الوقت الذي تمر فيه الطلبات عبر هذا الجزء من النظام ، $$$\ lambda$ - سرعة استلام الطلبات إلى النظام [pcs / s]. تكمن قوة النظرية في إمكانية تطبيقها على أي جزء من النظام: قائمة الانتظار ، أو المنفذ ، أو قائمة الانتظار + ، أو الشبكة بالكامل. غالبًا ما يتم استخدام هذه النظرية مثل هذا تقريبًا: "تدفق 1 جيجابت / ثانية يتدفق نحونا ، وقمنا بقياس متوسط ​​زمن الاستجابة ، وهو 10 مللي ثانية ، وبالتالي ، لدينا في المتوسط ​​1.25 ميغابايت في الرحلة." لذلك ، هذا الحساب غير صحيح. بتعبير أدق ، يكون هذا صحيحًا فقط إذا كانت جميع الطلبات لها نفس الحجم بالبايت. نظرية ليتل تحسب الاستعلامات في القطع ، وليس في البايت.

كيفية استخدام نظرية ليتل

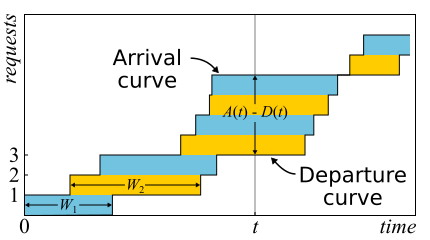
في الرياضيات ، غالباً ما يكون من الضروري دراسة الأدلة للحصول على رؤية حقيقية. هذا هو الحال فقط. نظرية ليتل جيدة لدرجة أنني أعطي رسمًا للرهان هنا. يتم وصف حركة المرور الواردة من خلال الوظيفة $$$A (t)$ - عدد الطلبات التي تم تسجيل دخولها في ذلك الوقت $$$t$ . بالمثل $$$D (ر)$ - عدد الطلبات التي تم تسجيل خروجها في ذلك الوقت $$$t$ . تعتبر لحظة دخول (خروج) الطلب لحظة استلام (إرسال) البايت الأخير. يتم تحديد حدود النظام فقط من خلال هذه الحالات الزمنية ، وبالتالي ، فإن النظرية قابلة للتطبيق على نطاق واسع. إذا رسمت رسومات بيانية لهذه الوظائف في نفس المحاور ، فمن السهل أن ترى ذلك $$$A (t) - D (t)$ هو عدد الطلبات في النظام في وقت ر ، و $$$W_n$ - وقت الاستجابة للطلب nth.

تم إثبات النظرية بشكل رسمي فقط في عام 1961 ، على الرغم من أن العلاقة نفسها كانت معروفة قبل ذلك بفترة طويلة.

في الواقع ، إذا كان من الممكن إعادة ترتيب الطلبات داخل النظام ، فسيكون كل شيء أكثر تعقيدًا ، لذلك من أجل البساطة سوف نفترض أن هذا لا يحدث. على الرغم من أن النظرية صحيحة في هذه الحالة أيضًا. الآن دعونا نحسب المساحة بين الرسوم البيانية. هناك طريقتان للقيام بذلك. أولاً ، وفقًا للأعمدة - كما تعتقد التكاملات عادةً. في هذه الحالة ، اتضح أن integrand هو حجم قائمة الانتظار بالقطع. ثانياً ، سطراً سطراً - ما عليك سوى إضافة كمون جميع الطلبات. من الواضح أن كلا الحسابين يعطيان المجال نفسه ، وبالتالي يكونا متساويين. إذا تم تقسيم كلا الجزأين من هذه المساواة على الوقت ،t ، حيث قمنا بحساب المنطقة ، فعندئذ على اليسار ، سيكون لدينا متوسط ​​طول قائمة الانتظار $$$L$ (بحكم المتوسط). على اليمين هو أكثر تعقيدا قليلا. نحتاج إلى إضافة عدد آخر من الطلبات N إلى البسط والمقام ، ثم سننجح

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

إذا أخذنا في الاعتبار فترة توظيف كبيرة أو كافية ، فسيتم إزالة الأسئلة الموجودة على الحواف ويمكن اعتبار أن النظرية مثبتة.

من المهم أن نقول أننا في الدليل لم نستخدم أي توزيعات لأي احتمالات. في الواقع ، نظرية ليتل هي قانون حتمية! وتسمى هذه القوانين في نظرية انتظار قانون التشغيل. يمكن تطبيقها على أي أجزاء من النظام وأي توزيعات لمتغيرات عشوائية مختلفة. تشكل هذه القوانين مُنشئًا يمكن استخدامه بنجاح لتحليل القيم المتوسطة في الشبكات. العيب هو أنها تنطبق فقط على المتوسطات ولا تقدم أي معرفة حول التوزيعات.

بالعودة إلى سؤال لماذا لا يمكن تطبيق نظرية ليتل على البايتات ، افترض ذلك $$$A (t)$ و $$$D (ر)$ الآن يتم قياسها ليس في القطع ، ولكن بالبايت. ثم ، بإجراء حجة مماثلة ، نحصل عليها بدلاً من ذلك $$$W$ الشيء الغريب هو المساحة مقسومة على العدد الإجمالي للبايت. لا يزال هناك ثوانٍ ، لكنه قليل الكمون المتوسط ​​المرجح حيث تزداد الطلبات الكبيرة. يمكن أن تسمى هذه القيمة متوسط ​​زمن الوصول للبايت - وهو ، بشكل عام ، منطقي ، لأننا استبدلنا القطع بالبايت - ولكن ليس كمون الطلب.

تقول نظرية ليتل إنه في ظل مجموعة معينة من الطلبات ، يكون زمن الاستجابة وعدد الطلبات في النظام متناسبين. إذا كانت جميع الطلبات تبدو متماثلة ، فلا يمكن تقليل متوسط ​​وقت الاستجابة دون زيادة الطاقة. إذا علمنا حجم الاستعلامات مقدمًا ، فيمكننا محاولة إعادة ترتيبها بالداخل لتقليل المساحة الواقعة بين $$$A (t)$ و $$$D (ر)$ وبالتالي متوسط ​​وقت استجابة النظام. واستمرارًا لهذه الفكرة ، يمكننا إثبات أن خوارزميات أقصر وقت للمعالجة وأقصر وقت للمعالجة المتبقية تعطي متوسط ​​وقت استجابة أدنى لخادم واحد دون إمكانية مزاحمته ، على التوالي. ولكن هناك تأثير جانبي - قد لا تتم معالجة الطلبات الكبيرة إلى أجل غير مسمى. تسمى هذه الظاهرة "الجوع" وترتبط ارتباطًا وثيقًا بمفهوم عدالة التخطيط ، والذي يمكن تعلمه من منشور الجدولة السابق : الأساطير والواقع .

هناك فخ آخر شائع يرتبط بفهم قانون ليتل. يوجد خادم ذو سلسلة واحدة يخدم طلبات المستخدمين. لنفترض أننا قمنا بقياس L - متوسط ​​عدد الطلبات في قائمة الانتظار لهذا الخادم ، و S - متوسط ​​وقت تقديم الخادم لطلب واحد. الآن النظر في طلب وارد جديد. في المتوسط ​​، يرى L استعلامات أمامه. خدمة كل منهم يستغرق في المتوسط ​​ثانية ثانية. اتضح أن متوسط ​​وقت الانتظار $$$W = L S$ . ولكن من خلال النظرية اتضح ذلك $$$W = L / \ lambda$ . إذا عدّلنا التعبيرات ، فسنرى هذا الهراء: $$$S = 1 / \ lambda$ . ما هو الخطأ في هذا المنطق؟

1. أول ما يلفت انتباهك: وقت استجابة النظرية لا يعتمد على S. في الواقع ، بالطبع ، لا. إن متوسط ​​طول قائمة الانتظار يأخذ هذا في الاعتبار بالفعل: كلما كان الخادم أسرع ، كلما كان طول قائمة الانتظار أقصر وأقصر وقت الاستجابة.
2. نحن نعتبر نظامًا لا تتراكم فيه قوائم الانتظار إلى الأبد ، ولكن تتم إعادة تعيينها بانتظام. هذا يعني أن استخدام الخادم أقل من 100٪ وتخطينا جميع الطلبات الواردة وبنفس السرعة التي وصلت بها هذه الطلبات ، مما يعني أنه في المتوسط ​​لا يستغرق الأمر ثوانٍ ثانية لمعالجة طلب واحد ، ولكن المزيد $$$1 / \ lambda$ ثواني ، لأنه ببساطة في بعض الأحيان لا نقوم بمعالجة أي طلبات. والحقيقة هي أنه في أي نظام مفتوح مستقر دون خسارة ، لا تعتمد الإنتاجية على سرعة الخوادم ، بل يتم تحديدها فقط من خلال دفق الإدخال.
3. الافتراض بأن الطلب الوارد يرى في النظام عددًا متوسطًا من الطلبات غير صحيح دائمًا. مثال مضاد: الطلبات الواردة تأتي بشكل دوري ، ونستطيع معالجة كل طلب قبل وصول الطلب التالي. صورة نموذجية للأنظمة في الوقت الحقيقي. يرى الطلب الوارد دائمًا طلبات صفرية في النظام ، ولكن من الواضح أن النظام يحتوي على أكثر من صفر طلبات. إذا كانت الطلبات تأتي في أوقات عشوائية تمامًا ، فعندئذ "يرون متوسط ​​عدد الطلبات" .
   
   
   
4. لم نأخذ في الاعتبار أنه مع وجود احتمال معين ، قد يكون هناك بالفعل طلب واحد في الخادم يحتاج إلى "تمديد". في الحالة العامة ، يختلف متوسط ​​وقت "ما بعد الخدمة" عن الوقت الأولي للخدمة ، وأحيانًا يكون من المفارقات أنه قد يكون أطول من ذلك بكثير. سوف نعود إلى هذه المشكلة في النهاية عندما نناقش الهجمات الصغيرة ، تابعنا.

لذلك ، يمكن تطبيق نظرية ليتل على الأنظمة الكبيرة والصغيرة ، وعلى قوائم الانتظار ، والخوادم ، وعلى سلاسل معالجة واحدة. لكن في كل هذه الحالات ، يتم تصنيف الطلبات عادة بطريقة أو بأخرى. طلبات المستخدمين المختلفين ، طلبات ذات أولويات مختلفة ، طلبات قادمة من مواقع مختلفة ، أو طلبات من أنواع مختلفة. في هذه الحالة ، المعلومات المجمعة حسب الفئات ليست مثيرة للاهتمام. نعم ، متوسط ​​عدد الطلبات المختلطة ومتوسط ​​وقت الاستجابة لجميعها متناسب مرة أخرى. ولكن ماذا لو أردنا معرفة متوسط ​​وقت الاستجابة لفئة معينة من الطلبات؟ والمثير للدهشة ، أن نظرية ليتل يمكن تطبيقها على فئة محددة من الاستعلامات. في هذه الحالة ، تحتاج إلى أن تأخذ كما $$$\ lambda$ المعدل الذي تطلبه هذه الفئة ، وليس الكل. ك $$$L$ و $$$W$ - متوسط ​​قيم عدد ووقت الإقامة لطلبات هذه الفئة في الجزء الذي تم التحقيق فيه من النظام.

أنظمة مفتوحة ومغلقة

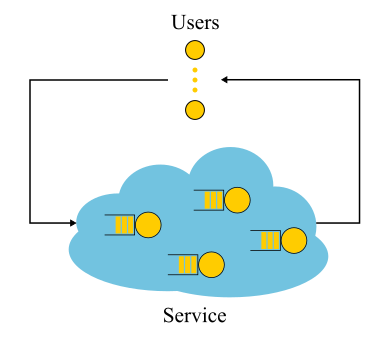
تجدر الإشارة إلى أنه بالنسبة للأنظمة المغلقة ، فإن خط الاستدلال "الخاطئ" يؤدي إلى الاستنتاج $$$S = 1 / \ lambda$ اتضح أن هذا صحيح. الأنظمة المغلقة هي تلك الأنظمة التي لا تأتي الطلبات من الخارج ولا تخرج من الخارج ، ولكن يتم تداولها من الداخل. أو ، خلاف ذلك ، أنظمة التغذية المرتدة: بمجرد أن يغادر الطلب النظام ، يحل الطلب الجديد مكانه. هذه الأنظمة مهمة أيضًا لأنه يمكن اعتبار أي نظام مفتوح مغمورًا في نظام مغلق. على سبيل المثال ، يمكنك اعتبار الموقع كنظام مفتوح ، حيث يتم باستمرار صب الطلبات ومعالجتها وسحبها ، أو على العكس من ذلك ، كنظام مغلق مع كامل جمهور الموقع. ثم يقولون عادة إن عدد المستخدمين ثابت ، وهم إما ينتظرون استجابة للطلب أو "يفكرون": لقد تلقوا صفحتهم ولم ينقروا بعد على الرابط. في حالة أن وقت التفكير يكون دائمًا صفراً ، يُسمى النظام أيضًا نظام الدُفعات.

قانون ليتل للأنظمة المغلقة صحيح إذا كانت سرعة الوصول الخارجي $$$\ lambda$ (ليسوا في نظام مغلق) استبدال مع عرض النطاق الترددي للنظام. إذا قمنا بلف الخادم ذو الترابط المفرد الذي تمت مناقشته أعلاه في نظام دفعي ، فسنحصل عليه $$$S = 1 / \ lambda$ و 100 ٪ إعادة التدوير. في كثير من الأحيان مثل هذه نظرة على النظام يعطي نتائج غير متوقعة. في التسعينيات ، كانت وجهة النظر هذه على الإنترنت مع المستخدمين كنظام واحد هي التي أعطت زخما لدراسة التوزيعات غير الأسية. سنناقش التوزيعات أكثر من ذلك ، ولكن هنا نلاحظ أنه في ذلك الوقت كان كل شيء تقريبًا وفي كل مكان يُعتبر أسيًا ، وحتى تم العثور على بعض المبررات ، وليس مجرد عذر بروح "معقد للغاية". ومع ذلك ، فقد تبين أن توزيعات التوزيعات المهمة ليست كلها ذات ذيول متساوية ، ويمكن تجربة معرفة ذيول التوزيع. ولكن الآن ، دعنا نعود إلى متوسط ​​القيم.

الآثار النسبية

لنفترض أن لدينا نظامًا مفتوحًا: شبكة معقدة أو خادم بسيط مترابط واحد - لا يهم. ما الذي سيتغير إذا قمنا بمضاعفة وصول الطلبات وتسريع معالجتها بمقدار النصف - على سبيل المثال ، من خلال مضاعفة سعة جميع مكونات النظام؟ كيف سيتغير الاستخدام والإنتاجية ومتوسط ​​عدد الطلبات في النظام ومتوسط ​​وقت الاستجابة؟ بالنسبة للخادم ذو الخيوط المفردة ، يمكنك محاولة أخذ الصيغ وتطبيقها "على الجبهة" والحصول على النتائج ، ولكن ماذا تفعل مع شبكة عشوائية؟ الحل بديهية على النحو التالي. لنفترض أنه تم مضاعفة الوقت ، ثم في "نظامنا المرجعي المتسارع" لا يبدو أن سرعة الخوادم وتدفق الطلبات يتغيران ؛ وفقا لذلك ، جميع المعلمات في الوقت المتسارع لها نفس القيم كما كان من قبل. وبعبارة أخرى ، فإن تسريع جميع "الأجزاء المتحركة" في أي نظام يعادل تسارع الساعة. الآن سنقوم بتحويل القيم إلى نظام في وقت عادي. لن تتغير الكميات التي لا تحتوي على أبعاد (الاستخدام ومتوسط ​​عدد الطلبات). تختلف القيم التي يتضمن بعدها العوامل الزمنية للدرجة الأولى تناسبيًا. سيتم مضاعفة إنتاجية [الطلبات / الطلبات] ، وسيتم خفض فترات الاستجابة والانتظار إلى النصف.

يمكن تفسير هذه النتيجة بطريقتين:

1. يمكن للنظام الذي تسارع مرات k أن يستوعب تدفق المهام k مرات أكثر ، ومع متوسط ​​زمن الاستجابة k مرات أقل.
2. يمكننا القول أن القوة لم تتغير ، ولكن ببساطة انخفض حجم المهام k مرة. اتضح أننا نرسل نفس الحمل إلى النظام ، ولكن يتم نشره في أجزاء أصغر. و ... أوه ، معجزة! يتم تقليل متوسط ​​زمن الاستجابة!

مرة أخرى ، لاحظت أن هذا صحيح بالنسبة لفئة واسعة من الأنظمة ، وليس فقط لخادم بسيط. من الناحية العملية ، هناك مشكلتان فقط:

1. لا يمكن تسريع جميع أجزاء النظام بسهولة. لا يمكننا التأثير على البعض على الإطلاق. على سبيل المثال ، سرعة الضوء.
2. لا يمكن تقسيم جميع المهام إلى ما لا نهاية إلى مهام أصغر وأصغر ، حيث لم يتم تعلم نقل المعلومات في أجزاء أقل من بت واحد.

النظر في مرور إلى الحد الأقصى. لنفترض ، في نفس النظام المفتوح ، التفسير رقم 2. نقسم كل طلب وارد إلى نصفين. وينقسم زمن الاستجابة أيضا إلى النصف. كرر التقسيم عدة مرات. ونحن لسنا بحاجة حتى إلى تغيير أي شيء في النظام. اتضح أنه يمكنك جعل وقت الاستجابة صغيرًا بشكل تعسفي بمجرد نشر الطلبات الواردة في عدد كبير بما فيه الكفاية من الأجزاء. في الحد الأقصى ، يمكننا أن نقول أنه بدلاً من الاستعلامات ، نحصل على "سائل الاستعلام" ، الذي نقوم بتصفيته بواسطة خوادمنا. هذا هو نموذج السائل المسمى ، وهو أداة مريحة للغاية للتحليل المبسط. ولكن لماذا زمن الاستجابة صفر؟ ما الخطأ الذي حدث؟ أين لم نعتبر الكمون؟ اتضح أننا لم نأخذ في الاعتبار سرعة الضوء فقط ، فلا يمكن مضاعفتها. لا يمكن تغيير وقت الانتشار في قناة الشبكة ، يمكنك فقط تحمله. في الواقع ، يتضمن الإرسال عبر شبكة مكونين: وقت الإرسال ووقت الانتشار. يمكن تسريع الأول بزيادة الطاقة (عرض القناة) أو تقليل حجم الحزم ، والثاني صعب للغاية التأثير. في "نموذجنا السائل" ، لم يكن هناك أي خزانات لتراكم السوائل - قنوات الشبكة مع أوقات انتشار غير صفرية وثابتة. بالمناسبة ، إذا أضفناهم إلى "نموذجنا السائل" ، فسيتم تحديد زمن الانتقال من خلال مجموع أوقات الانتشار ، وستظل قوائم الانتظار في العقد فارغة. تعتمد قوائم الانتظار فقط على أحجام الرزم وتقلب (تدفق القراءة) لدفق الإدخال.

ويترتب على ذلك أنه عندما يتعلق الأمر بالاختفاء ، لا يمكنك متابعة حساب التدفقات ، وحتى أجهزة إعادة التدوير لا تحل كل شيء. من الضروري أن نأخذ في الاعتبار حجم الطلبات وألا ننسى وقت التوزيع ، الذي يتم تجاهله في كثير من الأحيان في نظرية قائمة الانتظار ، على الرغم من أن إضافته إلى الحسابات ليست صعبة على الإطلاق.

توزيعات

ما هو سبب الاصطفاف؟ من الواضح أن النظام لا يملك سعة كافية ، ويتراكم الفائض من الطلبات؟ ليس صحيحا! تنشأ قوائم الانتظار أيضًا في الأنظمة التي توجد بها موارد كافية. إذا لم تكن هناك سعة كافية ، فإن النظام ، كما يقول المنظرين ، غير مستقر. هناك سببان رئيسيان لقائمة الانتظار: عدم انتظام الطلبات وتغير حجم الطلبات. لقد درسنا بالفعل مثالًا تم فيه القضاء على هذين السببين: نظام في الوقت الفعلي حيث تأتي الطلبات من نفس الحجم بشكل دوري بشكل صارم. قائمة الانتظار لا تشكل أبداً. متوسط ​​وقت الانتظار في قائمة الانتظار هو صفر. , , , . , .

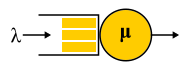
A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

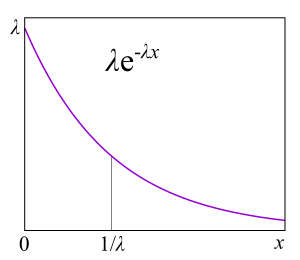
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . $$$a=1.16$ , 80/20: 20% 80% .

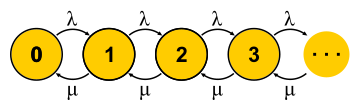
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ . , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ اين $$$\rho = \lambda / \mu$ - هذا هو استخدام الخادم. نهاية القصة. خلال العرض التقديمي ، فاتني قدر كافٍ من الافتراضات وقمت ببديلين من المفاهيم ، لكن جوهر هذا الأمل ، كما آمل ، لم يعاني.

من المهم أن نفهم أن هذا النهج لا يعمل إلا إذا كانت الحالة الحالية للآلة تحدد بالكامل سلوكها الإضافي ، وقصة كيف دخلت هذه الحالة ليست مهمة. لفهم كل يوم لآلة الحالة المحدودة ، هذا غني عن القول - بعد كل شيء ، هو شرط لذلك. لكن بالنسبة لعملية الاستوكاستك ، يستنتج من ذلك أن جميع التوزيعات يجب أن تكون أسي ، لأنهم فقط لا يملكون ذاكرة - لديهم معدل فشل ثابت.

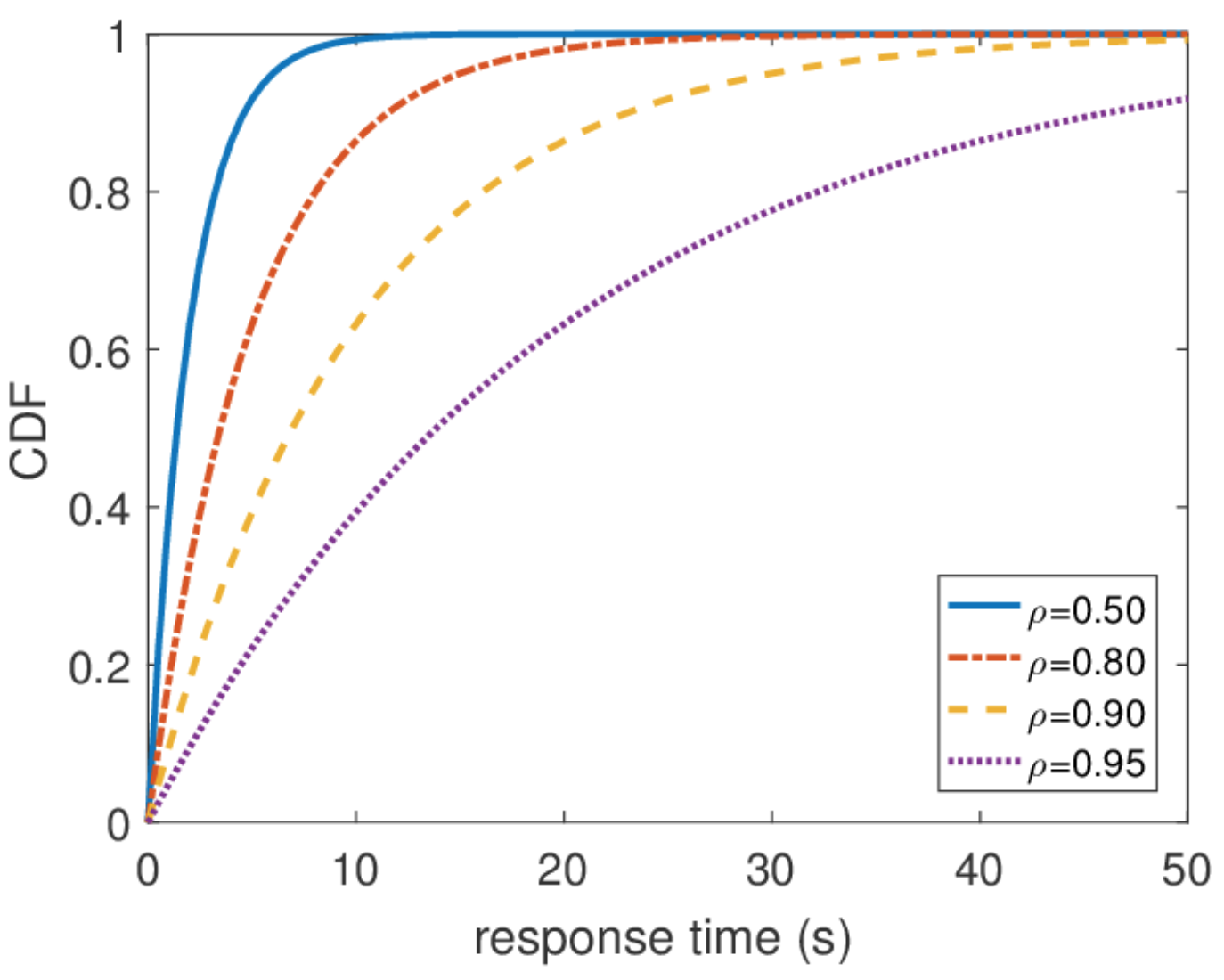
من المهم أيضًا أن نقول إن جميع المعلومات الأخرى حول النظام يسهل الحصول عليها إذا علمنا توزيع التوازن. متوسط ​​عدد الاستعلامات في النظام هو متوسط ​​هذا التوزيع. لمعرفة متوسط ​​وقت الاستجابة ، نطبق نظرية ليتل على عدد الاستعلامات. من الصعب العثور على توزيع وقت الاستجابة ، ولكن أيضًا في بعض الإجراءات يمكنك معرفة ذلك $$$\ mathbf {P} \ {response \ _time> t \} = e ^ {- (\ mu- \ lambda) t}$ وما هو متوسط ​​زمن الاستجابة $$$1 / (\ mu- \ lambda)$ .

وقت استجابة غير محدود

من هذا التوزيع ، يمكنك العثور على أي نسبة مئوية من وقت الاستجابة ، واتضح أن المئة في المئة تساوي اللانهاية. وبعبارة أخرى ، فإن أسوأ وقت للاستجابة لا يقتصر من أعلاه. وهو ، بشكل عام ، ليس مفاجئًا ، حيث استخدمنا دفق Poisson. ولكن في الممارسة العملية ، لا يمكن أبدا تلبية مثل هذا السلوك. من الواضح أن تدفق المدخلات من الطلبات إلى الخادم محدود ، على الأقل من خلال عرض قناة الشبكة لهذا الخادم ، وطول قائمة الانتظار محدد بواسطة الذاكرة على هذا الخادم. دفق Poisson ، على العكس من ذلك ، مع احتمال غير صفري يضمن حدوث رشقات نارية كبيرة بشكل تعسفي. لذلك ، لا أوصي بالاستمرار في افتراض دفق Poisson عند تصميم نظام إذا كنت مهتمًا بالنسب المئوية العالية وتحميل النظام كبير جدًا. من الأفضل استخدام نماذج حركة المرور الأخرى ، والتي سأتحدث عنها في وقت آخر عندما أتحدث عن حساب الشبكة.

التحجيم والضمانات

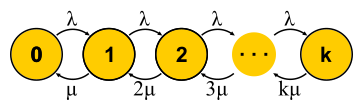
الآن وقد أصبح لدينا طريقة قوية بما يكفي لتحليل الأنظمة ، يمكننا محاولة تطبيقها على مهام مختلفة وجني الفوائد. هكذا تطورت نظرية الخدمة الجماهيرية في النصف الثاني من القرن العشرين. دعونا نحاول فهم ما تم تحقيقه. بادئ ذي بدء ، دعونا نعود إلى المهام التي حلها إرلانج. هذه هي المهام M / M / k / k و M / M / k ، والتي نود أن تحد من احتمال الفشل. اتضح أنه ليس من الصعب عليهم بناء سلاسل ماركوف. الفرق هو أنه مع إضافة المهام ، يزداد احتمال الانتقال العكسي ، حيث تبدأ المهام في المعالجة بالتوازي ، ولكن عندما يصبح عدد المهام مساوياً لعدد الخوادم ، يحدث التشبع. علاوة على ذلك ، بالنسبة إلى M / M / k / k ، تنتهي الشبكة ، وقد أصبح الأوتوماتون حقًا محدودًا ، ويتم رفض جميع الطلبات التي تصل إلى الحالة الأخيرة. احتمال هذا الحدث هو ببساطة مساوٍ لاحتمال أننا في الحالة الأخيرة.

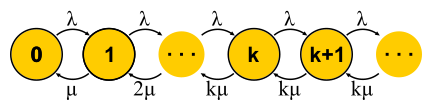
بالنسبة إلى M / M / k ، يكون الموقف أكثر تعقيدًا ، حيث يتم وضع قائمة الانتظار للطلبات ، وتظهر حالات جديدة ، لكن احتمال حدوث انتقال عكسي لا يزيد - تعمل جميع الخوادم بالفعل. تصبح الشبكة لانهائية ، كما هو الحال بالنسبة M / M / 1. بالمناسبة ، إذا كان عدد الطلبات في النظام محدودًا ، فستتضمن السلسلة دائمًا عددًا محدودًا من الحالات وسيتم حلها بطريقة أو بأخرى ، وهو أمر لا يمكن قوله عن السلاسل التي لا نهاية لها. في الأنظمة المغلقة ، تكون السلاسل دائمًا محدودة. حل الدوائر الموصوفة ل M / M / k / k و M / M / k ، وصلنا إلى الصيغة B و Erlang الصيغة C ، على التوالي. إنهم ضخمون إلى حد ما ، ولن أعطيهم ، لكن بمساعدتهم يمكنك الحصول على نتيجة مثيرة للاهتمام لتطوير الحدس ، والذي يطلق عليه قاعدة ملاك الجذر التربيعي. افترض أن هناك نظام M / M / k مع بعض دفق معين من الطلبات في الثانية الواحدة. افترض أن الحمل يجب أن يتضاعف بحلول يوم غد. والسؤال هو: كيفية زيادة عدد الخوادم بحيث يظل وقت الاستجابة كما هو؟ عدد الخوادم يحتاج إلى مضاعفة ، أليس كذلك؟ اتضح لا على الإطلاق. تذكر أننا رأينا بالفعل: إذا قمت بتسريع الوقت (الخوادم وتسجيل الدخول) بمقدار النصف ، فإن متوسط ​​وقت الاستجابة ينخفض ​​بمقدار النصف. العديد من الخوادم البطيئة والسريعة واحدة ليست هي نفس الشيء ، ولكن مع ذلك فإن قوة الحوسبة هي نفسها. على وجه الخصوص ، بالنسبة إلى M / M / 1 ، على سبيل المثال ، فإن وقت الاستجابة يتناسب عكسيا مع حجم "السعة المجانية" $$$\ mu - \ lambda$ ويتحدد فقط من خلال هذا المجلد. عند مضاعفة كلاً من قوة التدفق والمعالجة ، تتضاعف السعة الحرة للنظام: $$$2 \ mu - 2 \ lambda$ . قد يبدو أنه لحل المشكلة ، تحتاج فقط إلى توفير السعة المجانية ، ولكن وقت الاستجابة في M / M / k يتحدد بالفعل بواسطة صيغة Erlang الأكثر تعقيدًا. اتضح أنه يجب الحفاظ على السعة المجانية بما يتناسب مع الجذر التربيعي لعدد "الخوادم المشغولة" من أجل الحفاظ على نفس وقت الاستجابة. يُقصد بعدد "الخوادم المزدحمة" إجمالي عدد الخوادم مضروبة في الاستخدام: هذا هو الحد الأدنى لعدد الخوادم اللازمة للتشغيل المستقر.

باستخدام هذه القاعدة ، يحاولون في بعض الأحيان تبرير كيفية توسيع كتلة مع الخوادم. لكن لا تتخيل أن أي كتلة هي نظام M / M / k. على سبيل المثال ، إذا كان لديك موازن في مدخلاتك يرسل طلبات في قوائم الانتظار إلى الخوادم ، فلم يعد هذا M / M / k ، لأن M / M / k تتضمن قائمة انتظار شائعة تلتقط الخوادم منها الطلبات عند إصدارها. ولكن هذا النموذج مناسب ، على سبيل المثال ، لتجمعات مؤشرات الترابط مع قائمة انتظار FIFO شائعة. ومع ذلك ، حتى في هذه الحالة ، تجدر الإشارة إلى أن هذه القاعدة تقريبية للحالة عندما يكون هناك الكثير من مؤشرات الترابط. في الواقع ، إذا كان لديك أكثر من 10 سلاسل ، يمكنك أن تفترض بأمان أن هناك الكثير منها. حسنًا ، لا تنسَ توزيعات الأسية في كل مكان: من دون افتراض الأسية لجميع التوزيعات ، فإن القاعدة أيضًا لا تعمل.

وقت استجابة الشبكة

في نهاية المطاف ، تهم شبكة M / M / k متصلة على الأقل في سلسلة ، لأننا نصنع أنظمة موزعة. لدراسة الشبكات ، أود الحصول على مُنشئ: قواعد بسيطة وواضحة لربط العناصر المعروفة بكتل. في نظرية التحكم ، على سبيل المثال ، هناك وظائف نقل يتم دمجها بشكل مفهوم مع الاتصالات التسلسلية أو المتوازية. هنا ، يحتوي دفق الإخراج من أي عقدة على توزيع معقد للغاية ، باستثناء M / M / k ، والذي ، وفقًا لنظرية Burke المعروفة ، ينتج تيار Poisson مستقل. هذا الاستثناء ، كما تعتقد ، يستخدم بشكل أساسي.

اتصال تدفقات Poisson اثنين هو تيار Poisson. الفصل الاحتمالي لتيار بواسون إلى قسمين مرة أخرى يعطي تدفقات بواسون. كل هذا يؤدي إلى حقيقة أن جميع قوائم الانتظار في النظام هي كما لو كانت مستقلة ، ويمكنك الحصول ، في لغة رسمية ، على ما يسمى الحل شكل المنتج . أي أن التوزيع المشترك لأطوال قوائم الانتظار هو ببساطة نتاج توزيعات أطوال جميع قوائم الانتظار ، يتم النظر فيها بشكل منفصل - هكذا يتم التعبير عن الاستقلال في نظرية الاحتمالات. نجد فقط تدفقات الإدخال إلى جميع العقد ونستخدم الصيغ لكل عقدة بشكل مستقل. هناك عدد من القيود:

1. خوارزمية التوجيه الاحتمالي. يحدد الطلب المقدم من العقدة التالي بشكل عشوائي باحتمال معروف. هذا ليس سيئًا كما قد يبدو ، لأنه من الممكن استخدام "فئات الطلبات": قل أن جميع طلبات Vasya تأتي إلى الخادم رقم 1 ، ثم إلى الخادم رقم 2 ثم تخرج من الشبكة ، وتذهب طلبات Petya إلى الخادم رقم 2. ثم ، بعد الاحتمال المتساوي ، قم بزيارة الخادم رقم 1 أو الرقم 3 والخروج. أي أنه لا يلزم أن تكون جميع التحولات عشوائية ، فقد يكون للبعض أو حتى جميعها احتمال بنسبة 100٪.
2. افتراض استقلال كلاينروك. لا يمكن أن يعتمد وقت معالجة الطلب على محفوظات أو فئة الطلب ، ولكن يتم تحديده فقط من قبل الخادم ، وعندما يمر الطلب مرة أخرى عبر نفس الخادم ، يتم تحديده بشكل عشوائي في كل مرة. في الواقع ، لا توجد طريقة لتعيين حجم الطلب الذي سيتم استخدامه في خوادم مختلفة ، ويتم تحديد وقت الخدمة فقط بواسطة الخادم نفسه. يمكنك أيضا محاولة للالتفاف على هذا القيد. لهذا ، عادةً ما يتم استخدام التوجيه الاحتمالي ويتم إجراء حلقة للعودة إلى نفس الخادم مع بعض الاحتمالات - كما لو أنهم أعدوا تشغيل الطلب. في رأيي ، هذه خدعة غريبة إلى حد ما ، لأن مثل هذا الطلب يعيد إدخال قائمة الانتظار ، ولا يتم تنفيذه على الفور ، لكن بالنسبة لبعض المهام ، هذا ليس مهمًا.
3. Poisson حركة المرور المدخلات ووقت الخدمة الأسية على جميع العقد.

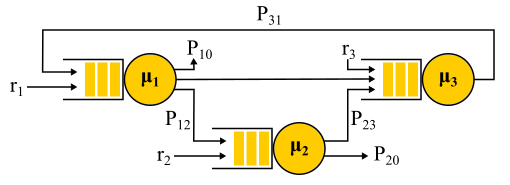
مثال شبكة جاكسون.

تجدر الإشارة إلى أنه في ظل وجود تغذية مرتدة ، لا يتم الحصول على دفق Poisson ، حيث تتحول التدفقات إلى بعضها البعض. عند إخراج عقدة التغذية المرتدة ، يتم أيضًا الحصول على دفق غير Poisson ، ونتيجة لذلك ، تصبح جميع التدفقات غير Poisson. ومع ذلك ، بطريقة مدهشة ، اتضح أن كل هذه التدفقات غير Poisson تتصرف تمامًا مثل تدفقات Poisson (أوه ، نظرية الاحتمالات هذه) إذا تم استيفاء القيود المذكورة أعلاه. ثم مرة أخرى نحصل على حل على شكل منتج. تسمى هذه الشبكات شبكات Jackson ، ويمكنها تقديم تعليقات ، وبالتالي ، زيارات متعددة لأي خادم. هناك شبكات أخرى يُسمح فيها بمزيد من الحريات ، لكن كنتيجة لذلك ، تتضمن جميع الإنجازات التحليلية المهمة لنظرية الطابور فيما يتعلق بالشبكات تدفقات Poisson على حل المدخلات وشكل المنتج ، الذي أصبح موضوع انتقادات لهذه النظرية وأدى في التسعينيات إلى تطوير نظريات أخرى ، ودراسة ما هو مطلوب بالفعل التوزيع وكيفية العمل معهم.

أحد التطبيقات المهمة لهذه النظرية الكاملة لشبكات جاكسون هو نمذجة الرزم في شبكات IP وشبكات الصراف الآلي. النموذج مناسب تمامًا: لا تختلف أحجام الرزم كثيرًا ولا تعتمد على الرزمة نفسها ، فقط على عرض القناة ، لأن وقت الخدمة يتوافق مع وقت إرسال الرزمة إلى القناة. وقت الإرسال العشوائي ، على الرغم من أنه يبدو وحشيًا ، إلا أنه في الواقع لا يحتوي على تباين كبير. علاوة على ذلك ، اتضح أنه في شبكة ذات وقت خدمة حتمية ، لا يمكن أن يكون زمن الوصول أكبر من شبكة جاكسون المماثلة ، لذلك يمكن استخدام هذه الشبكات بأمان لتقدير وقت الاستجابة من الأعلى.

توزيعات غير استثنائية

جميع النتائج التي تحدثت عنها كانت مرتبطة بتوزيعات الأسية ، لكنني ذكرت أيضًا أن التوزيعات الحقيقية مختلفة. هناك شعور بأن هذه النظرية كلها غير مجدية. هذا ليس صحيحا تماما. هناك طريقة لدمج توزيعات أخرى في هذا الجهاز الرياضي ، علاوة على ذلك ، عملياً أي توزيعات ، ولكن سيكلفنا شيئًا ما. باستثناء حالات قليلة مثيرة للاهتمام ، تضيع فرصة الحصول على حل في نموذج صريح ، ويضيع حل نموذج المنتج ، ومعه المُنشئ: يجب حل كل مشكلة تمامًا من نقطة الصفر باستخدام سلاسل Markov. هذه مشكلة كبيرة من الناحية النظرية ، ولكنها تعني في الممارسة العملية ببساطة تطبيق الطرق العددية وتجعل من الممكن حل مشكلات أكثر تعقيدًا وقريبة من الواقع.

طريقة المرحلة

الفكرة بسيطة. لا تسمح لنا سلاسل Markov بأن يكون لدينا ذاكرة داخل ولاية واحدة ، وبالتالي يجب أن تكون جميع التحولات عشوائية مع توزيع الأسي للوقت بين اثنين من التحولات. ولكن ماذا لو كانت الدولة مقسمة إلى عدة بدائل؟ يجب أن يكون للتحولات بين البدائل توزيع أسي إذا أردنا أن يظل الهيكل بأكمله سلسلة ماركوف ، ونريد ذلك حقًا ، لأننا نعرف كيفية حل هذه السلاسل. غالبًا ما تسمى الحالات الفرعية المراحل إذا تم ترتيبها في سلسلة ، وعملية التقسيم تسمى طريقة الطور.

أبسط مثال. تتم معالجة الطلب على عدة مراحل: أولاً ، على سبيل المثال ، نقرأ البيانات اللازمة من قاعدة البيانات ، ثم نقوم بإجراء بعض الحسابات ، ثم نكتب النتائج إلى قاعدة البيانات. لنفترض أن كل هذه المراحل الثلاث لها نفس التوزيع الأسي للوقت. ما التوزيع لديه وقت العبور من جميع المراحل الثلاث معا؟ هذا هو توزيع إرلانج.



ولكن ماذا لو قمت بإجراء العديد من المراحل متطابقة قصيرة؟ في الحد ، نحصل على توزيع حتمية. وهذا هو ، من خلال بناء سلسلة ، يمكنك تقليل تقلب التوزيع.

هل من الممكن زيادة التباين؟ سهل بدلاً من سلسلة المراحل ، نستخدم فئات بديلة ، ونختار عشوائيًا واحدة منها. مثال يتم تنفيذ جميع الطلبات تقريبًا بسرعة ، ولكن هناك فرصة صغيرة في أن يتم توفير طلب ضخم ، والذي يستغرق وقتًا طويلاً. سوف يكون لهذا التوزيع انخفاض معدل الفشل. كلما طال انتظارنا ، زاد احتمال أن يندرج الطلب في الفئة الثانية.



بالاستمرار في تطوير طريقة المراحل ، وجد المنظرون أن هناك فئة من التوزيعات التي يمكنك من خلالها التعامل بدقة توزيع غير سلبي! تم تصميم توزيعة Coxian بواسطة طريقة الطور ، ونحن لسنا فقط مطالبين بالمرور عبر جميع المراحل ، وبعد كل مرحلة هناك بعض الاحتمال للإنجاز.



يمكن استخدام هذا النوع من التوزيع على حد سواء لإنشاء دفق مدخلات غير Poisson ، ولإنشاء وقت خدمة غير أسي. هنا ، على سبيل المثال ، سلسلة Markov لنظام M / E2 / 1 مع توزيع Erlang لوقت الخدمة. يتم تحديد الحالة بواسطة زوج من الأرقام (n ، s) ، حيث n هو طول قائمة الانتظار ، و s هو رقم المرحلة حيث يوجد الخادم: الأول أو الثاني. جميع مجموعات من n و s ممكنة. تتغير الرسائل الواردة فقط n ، وعند الانتهاء من المراحل ، فإنها تتناوب وتقلل من طول قائمة الانتظار بعد الانتهاء من المرحلة الثانية.

لديك microbursts!

هل يمكن للنظام المملوء بنصف سعته أن يبطئ؟ بصفتنا أول موضوع اختبار ، نقوم بإعداد M / G / 1. المقدمة: يتدفق Poisson عند مدخل التوزيع والتوزيع التعسفي لوقت الخدمة. النظر في مسار طلب واحد من خلال النظام بأكمله. يظهر طلب وارد وارد بشكل عشوائي في قائمة الانتظار أمام نفسه متوسط ​​عدد الوقت للطلبات $$$\ mathbf {E} [N_Q]$ . متوسط ​​وقت المعالجة لكل منهم $$$\ mathbf {E} [S]$ . مع احتمال يساوي التخلص منها $$$\ rho$ ، هناك طلب آخر في الخادم ، والذي يجب أولاً "خدمته" في الوقت المناسب $$$\ mathbf {E} [S_e]$ . تلخيص ، نحصل على إجمالي وقت الانتظار في قائمة الانتظار $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e]$ . بواسطة نظرية ليتل $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ؛ الجمع ، نحصل على:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

بمعنى ، يتم تحديد وقت الانتظار في قائمة الانتظار بواسطة عاملين. الأول هو تأثير استخدام الخادم ، والثاني هو متوسط ​​وقت ما بعد الخدمة. النظر في العامل الثاني. طلب يصل في مرحلة ما $$$t$ ، ترى أن الرعاية اللاحقة تستغرق وقتًا $$$S_e (t)$ .



متوسط ​​الوقت $$$\ mathbf {E} [S_e]$ يحددها متوسط ​​قيمة الوظيفة $$$S_e (t)$ أي أن مساحة المثلثات مقسومة على إجمالي الوقت. من الواضح أننا يمكن أن نقتصر على مثلث واحد "متوسط" ، إذن $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ . هذا غير متوقع إلى حد ما. لقد تلقينا أن وقت ما بعد الخدمة لا يتم تحديده فقط من خلال متوسط ​​قيمة وقت الخدمة ، ولكن أيضًا حسب تباينه. التفسير بسيط. احتمال الوقوع في فاصل طويل $$$S$ أكثر من ذلك ، هو في الواقع يتناسب مع مدة S من هذا الفاصل. هذا ما يفسر وقت الانتظار الشهير Paradox ، أو التفتيش Paradox. لكن العودة إلى M / G / 1. إذا قمت بدمج كل ما حصلنا عليه وإعادة كتابته باستخدام التباين $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ الحصول على صيغة بولاشيك خينشين الشهيرة:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2} (C ^ 2_S + 1)$$

إذا كان الإثبات قد أصابك بالملل ، آمل أن ترضي نتيجة تطبيقه في الممارسة العملية. لقد فحصنا بالفعل بيانات وقت الخدمة في RTMR. الذيل الطويل ينشأ فقط مع تباين كبير ، وفي هذه الحالة $$$C ^ 2_S = 381$ . هذا ، كما ترى ، هو أكثر بكثير من $$$C ^ 2_S = 1$ للتوزيع الأسي. في المتوسط ​​، كل شيء بسرعة فائقة: $$$\ mathbf {E} [S] = 263.792 μs$ . لنفترض الآن أن RTMR تم تصميمه بواسطة نظام M / G / 1 ، والسماح بعدم تحميل النظام بشكل كبير ، التخلص $$$\ rho = 0.5 دولا$ . استبدال في الصيغة ، نحصل عليها $$$\ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263.792 μs = 50 ms$ . بسبب انفجار الميكروبات ، حتى أن هذا النظام السريع وغير المستغل يمكن أن يتحول في المتوسط ​​إلى نظام مثير للاشمئزاز. لمدة 50 مللي ثانية ، يمكنك الانتقال إلى محرك الأقراص الثابت 6 مرات أو ، إذا كنت محظوظًا ، حتى إلى مركز بيانات في قارة أخرى! بالمناسبة ، بالنسبة إلى G / G / 1 ، يوجد تقريب يأخذ في الاعتبار تباين حركة المرور الواردة: يبدو تمامًا ، فقط بدلاً من ذلك $$$C ^ 2_S + 1$ إنه مجموع كلا النوعين $$$C ^ 2_S + C ^ 2_A$ . بالنسبة إلى الخوادم المتعددة ، تكون الأمور أفضل ، لكن تأثير الخوادم المتعددة يؤثر فقط على العامل الأول. يبقى تأثير التباين: $$$\ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2$ .

كيف تبدو microburst؟ فيما يتعلق بتجمعات مؤشرات الترابط ، فهذه هي المهام التي تتم خدمتها بسرعة كافية بحيث لا تكون مرئية في جداول إعادة التدوير ، وبطيئة بما يكفي لإنشاء قائمة انتظار خلفها والتأثير على وقت استجابة التجمع. من وجهة نظر نظرية ، هذه استفسارات ضخمة من ذيل التوزيع. دعنا نفترض أن لديك مجموعة من 10 سلاسل ، وأنت تنظر إلى جدول إعادة التدوير ، المبني على مقاييس وقت التشغيل والتوقف ، والتي يتم جمعها كل 15 ثانية. بادئ ذي بدء ، قد لا تلاحظ أن مؤشر ترابط واحد معلق على الإطلاق ، أو أن جميع الخيوط العشر تنفذ مهام كبيرة في وقت واحد لمدة ثانية ، ثم لم تفعل شيئًا لمدة 14 ثانية. دقة 15 ثانية لا تسمح لرؤية قفزة في استخدام ما يصل إلى 100 ٪ والعودة إلى 0 ٪ ، وزمن الاستجابة يعاني. , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . الحل. $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ . $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ .

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. , , , , Robert B. Cooper. , .