إن أخذ عينات الخزان (المهندس "أخذ عينات الخزان") هو خوارزمية بسيطة وفعالة لأخذ عينات عشوائية من عدد معين من العناصر من ناقل موجود بحجم كبير و / أو غير معروف مسبقًا. لم أجد أي مقال عن هذه الخوارزمية حول هابري ولذلك قررت أن أكتبها بنفسي.
لذلك ، ما الذي نتحدث عنه. اختيار عنصر عشوائي واحد من ناقل هو مهمة أولية:
مهمة "إرجاع العناصر العشوائية K من ناقل الحجم N" مهمة أصعب بالفعل. هنا يمكنك بالفعل ارتكاب خطأ - على سبيل المثال ، خذ عناصر K الأولى (هذا ينتهك متطلبات العشوائية) أو خذ كل عنصر من العناصر مع احتمال K / N (هذا ينتهك متطلبات أخذ عناصر K بالضبط). بالإضافة إلى ذلك ، من الممكن تنفيذ حل صحيح رسميًا ، ولكن غير فعال للغاية "مزج جميع العناصر بشكل عشوائي واتخاذ K أولاً." وكل شيء يصبح أكثر إثارة للاهتمام إذا أضفنا الشرط الذي يشير إلى أن N هو عدد كبير جدًا (ليس لدينا ذاكرة كافية لحفظ جميع العناصر N) و / أو غير معروف مقدمًا. على سبيل المثال ، تخيل أن لدينا نوعًا من الخدمة الخارجية التي ترسل لنا عناصر واحدة تلو الأخرى. لا ندري كم سيأتي منها جميعًا ، ولا يمكننا حفظها جميعًا ، لكننا نريد أن يكون لدينا مجموعة من عناصر K المحددة بشكل عشوائي تمامًا من العناصر التي تم استلامها في أي وقت.
تسمح لنا خوارزمية أخذ عينات الخزان بحل هذه المشكلة في خطوات O (N) وذاكرة O (K). في هذه الحالة ، ليس مطلوبًا معرفة N مقدمًا ، وسيتم ملاحظة حالة أخذ العينات العشوائية لعناصر K تمامًا.
لنبدأ بمهمة مبسطة.
دع K = 1 ، أي نحتاج إلى تحديد عنصر واحد فقط من جميع العناصر الواردة - ولكن حتى يكون لكل عنصر من العناصر نفس احتمال التحديد. تقترح الخوارزمية نفسها:
الخطوة 1 : تخصيص الذاكرة لعنصر واحد بالضبط. نحن حفظ فيه وصل العنصر الأول.

حتى الآن ، كل شيء على ما يرام - لقد حان عنصر واحد فقط لنا ، مع احتمال 100 ٪ (في الوقت الراهن) ينبغي اختياره - هو عليه.
الخطوة 2 : تتم إعادة كتابة العنصر الثاني الوارد باحتمال قدره 1/2 باعتباره العنصر المحدد.

هنا أيضًا ، كل شيء على ما يرام: حتى الآن ، جاء إلينا عنصران فقط. بقي الخيار الأول محتملاً باحتمال قدره 1/2 ، وأعاد الثاني كتابته باحتمال قدره 1/2.
الخطوة 3 : تتم إعادة كتابة العنصر الثالث الوارد باحتمال 1/3 باعتباره العنصر المحدد.
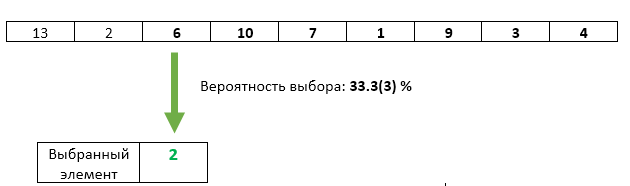
كل شيء على ما يرام مع العنصر الثالث - فرصته للاختيار هي 1/3 بالضبط. لكن هل انتهكنا بأي حال الفرص المتساوية للعناصر السابقة؟ رقم احتمال عدم الكتابة فوق العنصر المحدد في هذه الخطوة هو 1 - 1/3 = 2/3. وبما أننا في الخطوة 2 ، قمنا بضمان فرص متساوية لكل عنصر من العناصر التي سيتم تحديدها ، وبعد الخطوة 3 يمكن اختيار كل عنصر بفرصة 2/3 * 1/2 = 1/3. بالضبط نفس الفرصة مثل العنصر الثالث.
الخطوة N : مع احتمال 1 / N ، تتم إعادة كتابة رقم العنصر N كما هو محدد. كل عنصر من العناصر السابقة التي وصلت لديه نفس فرصة 1 / N للبقاء محددة.
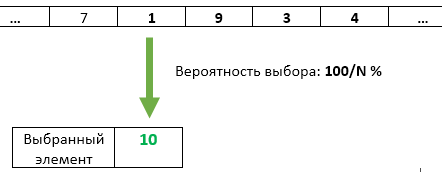
لكنها كانت مهمة مبسطة ، مع K = 1.
كيف ستتغير الخوارزمية لـ K> 1؟
الخطوة 1 : نحن نخصص الذاكرة على عناصر K. نكتب فيه وصلت أول عناصر K.

الطريقة الوحيدة لأخذ عناصر K من العناصر K وصلت هي أن تأخذهم جميعًا :)
الخطوة N : (لكل N> K): قم بإنشاء رقم عشوائي X من 1 إلى N. إذا كان X> K ، فإننا نتجاهل هذا العنصر وننتقل إلى التالي. إذا كانت X <= K ، فقم بإعادة كتابة العنصر بالرقم X. نظرًا لأن قيمة X ستكون عشوائيًا في النطاق من 1 إلى N ، تحت الشرط X <= K ، ستكون عشوائية بشكل موحد في النطاق من 1 إلى K. وبالتالي ، فإننا نضمن التوحيد اختيار العناصر القابلة لإعادة الكتابة.

كما ترون ، فإن كل عنصر تالي يأتي لديه فرصة أقل وأقل للاختيار. ومع ذلك ، سيكون دائمًا K / N (كما هو الحال بالنسبة لكل عنصر من العناصر السابقة التي وصلت).
تتمثل ميزة هذه الخوارزمية في أنه يمكننا التوقف في أي وقت ، وإظهار للمستخدم المتجه الحالي K - وسيكون هذا هو ناقل العناصر العشوائية المحددة بأمانة من تسلسل العناصر التي وصلت. ربما يناسب ذلك المستخدم ، أو ربما يريد متابعة معالجة القيم الواردة - يمكننا القيام بذلك في أي وقت. في هذه الحالة ، كما ذكرنا في البداية ، لا نستخدم أبدًا أكثر من ذاكرة O (K).
أوه نعم ، لقد نسيت تمامًا ، أخيرًا ، يتم تضمين دالة
std :: sample ، التي تعمل بالضبط ما هو موضح أعلاه ، في مكتبة C ++ 17 القياسية. المعيار لا يلزمه باستخدام أخذ عينات الخزان فقط ، ولكنه يلزمه بالعمل في خطوات O (N) - حسنًا ، من غير المحتمل أن يختار مطورو تطبيقه في المكتبة القياسية بعض الخوارزمية التي تستخدم أكثر من ذاكرة O (K) (وستفشل أقل من ذلك أيضًا) - يجب تخزين النتيجة في مكان ما).
المواد ذات الصلة