فرز "برج هانوي"

^{أبراج هانوي}
فقط كسول لم يكتب عن لعبة إدوارد لوك الشهيرة على هابري. يبدو أن جميع الأغطية ممزقة ولم يعد بالإمكان إضافة شيء آخر حول الخوارزمية. لكن لا ، هذا الموضوع لديه موارد خفية. اليوم ، على وجه الخصوص ، سوف نعيد الخوارزمية لحل هذا اللغز إلى نوع كامل. (لماذا؟ فقط للمتعة. الجمعة ممكن.)

هذا المنشور مخصص لذكرى المعلم الحقيقي للبرمجة Andrei Mrrl Astrelin ، الذي أوضح لي هذه الخوارزمية ذات مرة بكل بساطة وبشكل واضح. الكود الزائف أدناه هو نص مؤلفه.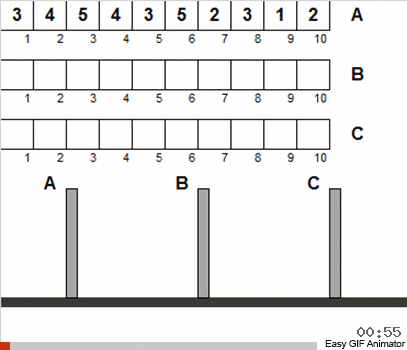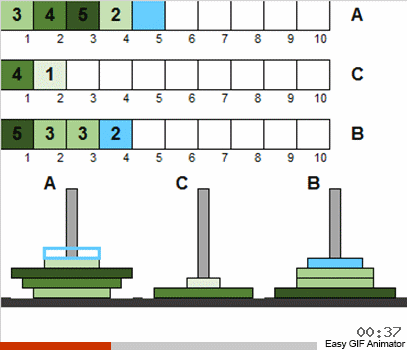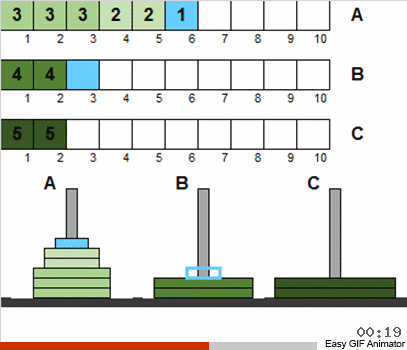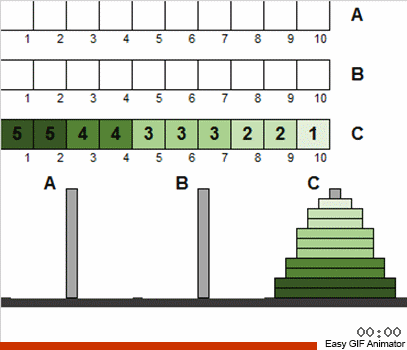


في اللغز الكلاسيكي ، يتم ترتيب الأقراص الموجودة على القطب الأول في البداية. لكننا سوف نسمح لهم بالتوتر في أي ترتيب.

بالإضافة إلى ذلك ، يُفترض أن أحجام القرص فريدة من نوعها. لن نتشبث بهذا التقييد ونسمح بالتكرار.

إذا سمحت لهاتين الحريتين فقط ، فيمكن تفسير الشروط الأولية للغز على أنه صفيف (الأقراص عبارة عن أرقام) ، والمهمة تتلخص في ضرورة فرز هذه المجموعة.

الشروط المتبقية التي لا نغيرها (تقريبًا):

• لدينا أعمدة مساعدة (زوج من المصفوفات الفارغة).
• يمكننا نقل أقراص واحدة في وقت واحد.
• وضع أحجام أصغر فقط على أحجام أكبر (نظرًا لأننا سمحنا بنفس أحجام القرص ، يمكنك أيضًا وضع القرص المنقول في الأعلى على الآخرين من نفس الحجم).
• لدينا الحق في مقارنة قرص محمول بالأقراص العلوية فقط (أي جميع المصفوفات الثلاثة مكدسات).

مهمتنا: أن تأخذ خوارزمية اللغز العودية الكلاسيكية ...

def hanoi(n, source, helper, target): if n > 0: hanoi(n - 1, source, target, helper) if source: target.append(source.pop()) hanoi(n - 1, helper, source, target) 

... وتحويلها إلى الفرز!

في الواقع ، من حقيقة أننا سمحنا للاضطراب والتكرار الأولي لحجم الأقراص ، لم يتغير شيء من هذا بشكل جذري. إلى حد كبير ، يتم حل المشكلة بنفس الطريقة العودية الكلاسيكية. أهم شيء يجب فهمه هو أن جميع حركات الأقراص تنقسم إلى عدة مراحل ، كل واحدة منها عبارة عن هانوي مصغر.

وهذا هو ، في كل مرحلة لا نعتبر جميع الأقراص المتوفرة ، ولكن فقط مجموع تلك التي تلبي الظروف القديمة. بعد فرز هذه المجموعة الصغيرة حسب الكلاسيكيات ، سنعمل على تقريب الحالة العامة للنظام من اللغز الكلاسيكي. ثم نأخذ مرة أخرى مجموعة الأقراص التي تتوافق مع الكلاسيكيات ونطبق الخوارزمية المعروفة مرة أخرى. وهذه المجموعة ستكون أكبر مما كانت عليه في الخطوة السابقة! وهكذا نكرر حتى تصبح جميع الأقراص الموجودة على كل الأعمدة فجأة مختلفة عن الحالة الكلاسيكية.

النظام الذي تم انتهاكه مبدئيًا (بسبب حقيقة أن الأقراص غير مرتبة عند الإدخال) هو معالجة ذاتية مع كل تكرار.

بالنسبة لقرار التكرار ، هذا لا يهم على الإطلاق. لأن الأقراص متطابقة متتالية ننتقل ببساطة كقرص واحد.

خوارزمية

نسمي الأعمدة A و B و C ( A في البداية غير فارغة).

نحن نقدم العمليات:

A -> C () - تحول قرص واحد من A إلى C.
أعلى (A) ، أعلى (C) - حجم القرص العلوي A أو C. إذا كان العمود فارغًا ، فهذا الحجم = MaxInt .
B -> C ( K ) - تحول من B إلى C كل الأقراص التي يقل حجمها عن K (يمكننا القيام بذلك إذا كانت الأقراص العليا A و C لا تقل عن K ).
المبادلة () - إعادة ترتيب العمودين B و C (أو إعادة تسميتهما - لا نهتم بمكان الأقراص).
بينما ( أ ) - حلقة حتى A فارغة.

ثم تعمل الخوارزمية التالية:

 //      A    ""  while(A) { K = top(A); //-""    while(top(C) < K){ B->C(top(C)); swap(); } A->C(); } // .  -  "" while(C) { B->C(top(C)); swap(); } 

© Mrrl

صعوبة

في أسوأ الحالات ، يميل الفرز إلى التعقيد الزمني للخوارزمية الكلاسيكية ، والتي رغم أنها بسيطة وأنيقة ، فهي في نفس الوقت غير فعالة إلى الحد الأقصى. بالنسبة للأفضل والمتوسط ​​، أجد صعوبة في تحمله.

أما بالنسبة للذاكرة ، فيمكننا القول أنه إذا تم استخدام العودية ، فستكون التكاليف مماثلة.

التنفيذ

لم أكتب روايتي الخاصة في بيثون (سأفعل ذلك لاحقًا). ومع ذلك ، في قسم "الروابط" أدناه ، نشرت بعض الروابط حيث يمكنك رؤية التطبيقات بلغات مختلفة. خيار مثير للاهتمام خاصة في جافا. لم يأخذ المؤلف كأساس الطريقة العودية المعروفة لحل اللغز ، لكنه بنى أقصر شجرة من المسارات. من المفترض أن هذا هو الحل الأكثر فاعلية إذا كتبت الفرز بأسلوب "برج هانوي".

خصائص الخوارزمية

المراجع

برج هانوي

تطبيقات: C ، جافا مقابل C ++ مقابل بيثون ، بيثون .

سلسلة المقالات:

• تطبيق اكسل AlgoLab.xlsm
• أنواع التبادل
• أنواع الإدراج
  • أمين المكتبة فرز
  • سوليتير فرز
  • فرز "برج هانوي"
  • فرز الشباب الجدول
  • عكس الترتيب
  • إدراج فرز المقارنة
• الترتيب حسب الاختيار
• دمج الأنواع
• الترتيب حسب التوزيع
• الفرز الهجين

في تطبيق AlgoLab ، أصبح هذا التصنيف متاحًا الآن. على الرغم من أنه ينتمي إلى فئة الأنواع حسب الإدخالات ، بسبب الإسراف في الخوارزمية ، يتم وضعها في قسم "أنواع أخرى". يوجد أيضًا قيود - يمكن أن تكون الأرقام في الصفيف المفروزة من 1 إلى 5 فقط (بسبب صعوبة تقديم الأقراص). سوف يتم استبدال الأرقام الأخرى بهذه.

يوجد أيضًا حد لحجم المصفوفة - لا يزيد عن 20 عنصرًا. يتم ذلك وفقًا لمصالحك الخاصة - إذا كنت تأخذ مجموعة كبيرة جدًا ، فقد يحدث أن تضطر إلى فرزها إلى سن مبكرة جدًا.

كُتِب هذا المقال بدعم من EDISON Software ، وهي شركة تقوم بتطوير إنارة المدينة الذكية احترافًا وتحتفظ بمواقع Python.