نظرية السعادة. الحوادث ليست عرضية؟

ما زلت أطلع قرّاء هبر على فصول كتابه "نظرية السعادة" بعنوان "الأسس الرياضية لقوانين المعنى". هذا لم ينشر بعد كتابًا علميًا شهيرًا ، يوضح بشكل غير رسمي كيف تسمح لك الرياضيات بالنظر إلى العالم وحياة الناس بدرجة جديدة من الوعي. إنه لمن يهتم بالعلم ولمن يهتم بالحياة. وبما أن حياتنا معقدة ولا يمكن التنبؤ بها إلى حد كبير ، فإن التركيز في هذا الكتاب ينصب أساسًا على نظرية الاحتمالات والإحصاءات الرياضية. هنا لم يتم إثبات النظريات ولم يتم تقديم أساسيات العلوم ، وهذا ليس كتابًا مدرسيًا على الإطلاق ، ولكن ما يسمى بالعلم الترويحي. لكن هذه المقاربة شبه المرحة على وجه التحديد هي التي تسمح لنا بتطوير الحدس وإلقاء المحاضرات على الطلاب بأمثلة حية ، وأخيرا ، شرح لغير المتخصصين في الرياضيات وأطفالنا أننا وجدنا مثل هذه الأشياء المثيرة للاهتمام في علومنا الجافة.



في هذا الفصل ، سنناقش رحلة العملات المحددة سلفًا والخرائط الطبوغرافية والكوارث الرياضية وطبيعة العشوائية. وعلى طول الطريق ، دعونا ننظر إلى أقسام الرياضيات مثل نظرية التدابير ونظرية الفوضى الديناميكية.

عادة ما يبدأ الحديث عن قوانين الخلاصة ، كمصدر للاضطراب اليومي ، بقانون السندوتشات الشهير. يتم صياغتها بسهولة والتحقق منها بسهولة ومعروفة على نطاق واسع:

شطيرة دائما يسقط الزبدة.

من الواضح أن كلمة "دائمًا" هنا هي مبالغة. من السهل أن نتخيل الظروف التي ستسقط فيها الساندويتش ، مع ترك الجانب المزيَّن سليماً. ماذا يفهم الناس بهذا القانون؟ على الأرجح ، تقع السندوتشات في كثير من الأحيان بشكل كافٍ لجعلها ملحوظة. ولكن هل النتيجة غير المواتية للسقوط أكثر احتمالا من السقوط؟ تختلف السندوتشات ، فهي تقع في ظروف مختلفة ، من ارتفاعات مختلفة ... هناك العديد من المعلمات التي قد لا تكون هناك فائدة في الحديث عن الأنماط في هذه المهمة. أي شيء يمكن أن يحدث. يحدث أن ينخفض ​​النفط ، ثم يصبح مهينًا ، ونتذكر القانون ونتذكره. وإذا كان السندويش غير مهتم - مع ارتفاع الزيت ، أو إذا كان بدون زيت على الإطلاق ، فلا يوجد شيء يمكن الحديث عنه - فمن الواضح أن القانون هزلي! في النهاية ، يشبه السندوتش عملة معدنية ، يستخدمها علماء الرياضيات للحصول على متغيرات عشوائية ذات قيمتين محتملتين: "النسر" و "ذيول". إذا كانت العملة "صادقة" ، فلا يهم إطلاقًا أي جانب يسقط ، ونقول إن احتمال سقوط النسر والذيل هو نفسه وعلى قدم المساواة $$$1/2$ . من الناحية النظرية ، يجب أن تكون السندويشات هي نفسها. سنعود إليهم في الفصل التالي ، ولكن الآن دعونا نلقي نظرة على النظام الاحتمالي البسيط على الأرجح - العملة المعدنية.

يتم قذف العملة المعدنية في التجارب النظرية الاحتمالية بطريقة سحرية خاصة ، بحيث لا يؤثر اختيار الموضع الأولي والسرعة الأولية وسرعة الدوران أثناء إرم على احتمال نتيجة محددة. لكن من الواضح أن هذا مستحيل! العملة المعدنية هي نظام ميكانيكي وتطيع قوانين الميكانيكا ، لكنها لا تحتوي على متغيرات عشوائية. المستقبل في قوانين الحركة من هذه الهيئة البسيطة مثل عملة معدنية يتحدد بشكل فريد من قبل الدولة الماضية لهذه الهيئة. إذا انقلب الروبوت بعملة معدنية ، أو كان لابلاس شيطان مخلوقًا أسطوريًا يحتوي على معلومات كاملة عن إحداثيات وسرعات أي نظام ميكانيكي ، فسيتم الحصول على نتائج مماثلة مع بيانات أولية ثابتة. بالطبع ، نحن لسنا روبوتات أو شياطين ، لكن هل يقوم الناس حقًا بإلقاء العملات المعدنية بطريقة قذرة ولا يمكن التنبؤ بها بحيث يمكن أن تؤدي قوانين الميكانيكا إلى حوادث؟

وأين ، بشكل عام ، هل تأتي العشوائية من العالم الموصوف بقوانين الميكانيكا؟ من أين يأتي عشوائي؟ ما هو الفرق بين النظم الفوضوية أو العشوائية حقًا ، والتي لا يمكن التنبؤ بها بشكل أساسي ، والأنظمة التي يصعب فيها ببساطة تخمين السلوك ، ولكن يمكن حسابه؟

تم اعتبار مشكلة العملة في عام 1986 من قبل جوزيف كيلر. نحن نقدم شرحًا بسيطًا لحدوث عدم اليقين في هذه العملية ، استنادًا إلى التفكير في مقالة كيلر. أي جانب سوف تسقط العملة يعتمد على وقت الرحلة. $$$t$ ومن السرعة الزاوية $$$\ أوميغا$ . إذا قمت بقياس السرعة الزاوية في الثورات لكل وحدة زمنية ، فسيتم التعبير عن عدد الثورات التي يتم إجراؤها بواسطة العملة ببساطة شديدة $$$n = t \ omega$ . يعين هذا الاعتماد أسطر عدد متساوٍ من الثورات في الإحداثيات $$$(t ، \ omega)$ وهم ، بدورهم ، يحدون من المناطق المقابلة لعدد من الثورات الفردية والزوجية.

رسم تخطيطي يوضح تكافؤ عدد الثورات التي تقوم بها عملة في الرحلة. يظهر المستطيل المنطقة التي تحدث فيها عملية الكهانة على العملة.

في مثل هذا الرسم البياني ، من الممكن إظهار ما ستكون عليه نتيجة النقود المعدنية ، الملتوية بعدد معروف من الثورات في الثانية ، ويتم التقاطها بعد وقت انعكاس معروف. إذا وقعنا في شريط أبيض ، فإن الجانب نفسه سينسحب وكان في المقدمة عند القذف ، إذا كان باللون البرتقالي - العكس. خطوط السرعة المتساوية هي خطوط زائدة ، ويمكن ملاحظة أنه كلما زادت السرعة ، أصبح تناوب المناطق أكثر وأكثر تكرارا ، وأصبحت المناطق نفسها أرق. اليد البشرية غير كاملة ويغطي مبعثر صغير جدًا من القيم الأولية العديد من المناطق في وقت واحد ، مما يجعل النتيجة غير متوقعة. في نطاق اليد (المستطيل في الرسم التخطيطي) ، إزاحة كافية $$$5 \٪$ للقفز من شريط أبيض إلى برتقالي. يبقى السؤال: كيف يتبع "الصدق" لعملة ميكانيكية حقيقية من هذا البناء؟ كيفية الحصول على احتمال فقدان النسر أو ذيول من الرسم البياني الناتج؟

اتخاذ إجراءات عاجلة!

سوف نغرق قليلاً في مثل هذه الرياضيات التي لا يتم تدريسها في المدرسة من أجل فهم أفضل لما نناقشه. قلنا في المقدمة أن علماء الرياضيات لا يدرسون الأرقام أو الأشكال الهندسية ، كما قد يبدو بعد دراسة دورة المدرسة. إنهم يعملون مع بنى رياضية (جبر مجردة ، حلقات نصفية ، حقول ، أحاديات ، مساحات طوبولوجية وأشياء مجردة أخرى) ، ويصفونها ، كما يبدو ، غير مرتبط تمامًا بالممارسة ، وتعريفهم ، ودراسة خصائصهم ، وإثبات النظريات. وبعد ذلك صقلوا مهاراتهم في العثور على مثل هذه الهياكل في مختلف مجالات المعرفة ، مما حقق اختراقات مفيدة بشكل مثير للدهشة ، بما في ذلك في المجالات التطبيقية البحتة. سنتطرق الآن إلى هذه الرياضيات قليلاً وننظر في كيفية بناء قاعدة نظرية الاحتمالات على أساس مفهوم مجرد للغاية للقياس.

وصفنا ميكانيكا العملة وحصلنا على المناطق التي تصف مجموعات من الحلول مع خصائص معينة. المناطق هي الأرقام المسطحة ، وكيفية الانتقال منها إلى الاحتمالات بشكل صحيح؟ نحن بحاجة إلى قياس مناطقنا ونأتي بشكل طبيعي إلى منطقتهم. المنطقة - هو مقياس للشخصية المسطحة. هذا هو المصطلح الرياضي الدقيق للدالة التي تربط مجموعة مع قيمة عددية غير سالبة معينة. أمثلة على المقاييس هي الكميات في مجموعات تعدادية (عدد التفاح في كيس ، على سبيل المثال) ، وكذلك طول المساحة وحجمها .

هناك قسم كامل في الرياضيات يسمى نظريات القياس . وُلدت هذه النظرية في مطلع القرنين التاسع عشر والعشرين (وقفت إميل بوريل وهنري ليبسج في أصلها) وفتحت أمام علماء الرياضيات فرصًا كثيرة لتحليل الأشياء المعقدة للغاية: مجموعات الكانتور والكسور. وشكلت أساس التحليل الوظيفي ونظرية الاحتمالات الحديثة ، والتي أسسها عالم الرياضيات الروسي الرائع أندريه كولموغوروف. يتيح لك تعريف الاحتمال ، كإجراء ، رؤية كل الخصائص الأساسية للاحتمال لكل من المجموعات المنفصلة والمستمرة.

على الرغم من أن كتابنا ليس كتابًا مدرسيًا ، إلا أنه من الضروري التوقف قليلاً عن النظر إلى مفاهيم احتمال الثوريوم من وجهة نظر الطيور والشعور بطعم الرياضيات. بادئ ذي بدء ، ندرج الخصائص الرئيسية لأي تدابير. لتخيلهم بشكل أفضل ، يمكنك استخدام الكلمات "كمية" أو "طول" أو "مساحة" بدلاً من كلمة "قياس".

1. قياس مجموعة فارغة هو صفر.
2. قياس المجموعة الكاملة القابلة للقياس محدد للتدابير المحدودة.
3. لا يتجاوز قياس المجموعة الفرعية مقياس المجموعة
4. إن مقياس اتحاد مجموعتين تعسفيين يساوي مجموع مقاييس هذه المجموعات ناقصًا مقياس تقاطعها (الإضافة).
5. مقياس استكمال مجموعة فرعية يساوي الفرق بين مقاييس المجموعة بأكملها وقياس المجموعة الفرعية.

هل يمكن لأي دالة عددية غير سالبة أن تكون مقياسًا؟ لا على الإطلاق. على سبيل المثال ، العمر يمنح الشخص رقمًا محددًا تمامًا. ولكن لا يمكن تعريف عمر شخصين بأنه مجموع أعمارهم. وسرعة الجري ليست قياسًا - فالشخصان لا يعملان بسرعة مرتين. لكن الزخم (الزخم) أو الطاقة له خصائص المقياس بالفعل. يمكن للوزن وكمية المال وكمية المعرفة وحجم البكاء ، رغم أنه ليس من السهل دائمًا قياس الأشياء ، أن يكون أيضًا مقياسًا لكثير من الناس.

على المستوى الحدسي ، يكون الجميع على دراية بمفهوم الاحتمال الآن. ويقدر العلماء السياسيون والصحفيون في البرامج الحوارية ، ويناقش الحديث عن ظاهرة الاحتباس الحراري أو أمطار الغد ، ويقال النكات حول ذلك: ما هو احتمال لقاء ديناصور على نهر تفير؟ - ثانية واحدة: إما اجتماع أم لا. في الرياضيات الحديثة ، يتم تعريف مفهوم الاحتمال على أنه مقياس على مجموعة خاصة تسمى مساحة الاحتمال . ويشمل كلا من الأحداث الأولية ومجموعاتها التي تم الحصول عليها باستخدام عمليات الاتحاد والتقاطع والاستبعاد. مثال على حدث أولي: "فقدان الثلاثي عند رمي العظام". مثال لحدث غير أساسي: "فقدان أي رقم زوجي باستثناء اثنين." لذلك ، ندرج خصائص الاحتمال:

1. احتمال وقوع حدث مستحيل هو صفر.
2. الاحتمال لكامل مساحة الاحتمال يساوي الوحدة.
3. إذا كان أحد الأحداث يستتبع أيضًا حدثًا آخر ، فعندئذ لا يتجاوز احتمال الثاني احتمال الأول. هنا العلاقة "تستلزم" للأحداث تعادل "مجموعة فرعية" للمجموعات ولا تعني "سبب".
4. احتمال وقوع حدث واحد على الأقل من حدثين تعسفيين يساوي مجموع احتمالات كل من هذه الأحداث ، مطروحًا منه احتمال حدوث الأحداث في وقت واحد.
5. احتمال وقوع حدث هو واحد ناقص احتمال وقوع حدث.

ألق نظرة فاحصة على خصائص التدابير والاحتمالات وسترى أننا نتحدث عن نفس الخصائص.

لا تنشأ كل خصائص الاحتمال من تعريفها كتدبير: مفاهيم استقلال الأحداث وطريقة حساب احتمال حدوث حدثين مستقلين أو أكثر في وقت واحد حيث يتم تقديم منتجات من الاحتمالات من خلال الاحتمال الشرطي ، ولكن هذه المفاهيم تتسق مع تعريف Kolmogorov.

تتوافق المتغيرات العشوائية المنفصلة مع مجموعات يمكن حصرها ، وفيها يكون التدبير الطبيعي هو عدد عادي لعدد العناصر. وفقًا لذلك ، فإن الاحتمال في فضاء احتمالي منفصل هو الحساب التوافقي للخيارات المألوفة لدى كل طالب. بالنسبة للمتغيرات العشوائية المستمرة ، يكون الاحتمال ، كإجراء ، أشبه بالطول أو المساحة ، وهنا نتحدث عن كثافات الاحتمالات .

القياس الاحتمالي مع التدبير لا ينتهي عند هذا الحد. ما هي القيمة المتوسطة ؟ هذا هو تناظر لموضع مركز كتلة الشكل الذي يتكون من كتل نقطية أو صلبة بكثافة معروفة. ويتم حساب هذه الكميات بنفس الطريقة. وكيف يتم تشتت المتغيرات العشوائية حول المتوسط: التباين ؟ تماما مثل لحظة الجمود تميز توزيع الكتلة حول مركز الكتلة. ومرة أخرى ، تتزامن الصيغ لحساب التباين لعينة أو توزيع مع الصيغ لحظة القصور الذاتي لمجموعة من الأجسام أو جسم صلب ذي شكل ماكر.

بالمناسبة ، إذا استبدلنا تعريفات وخصائص الاحتمال بالمبلغ بـ "الحد الأقصى" والمنتج بـ "الحد الأدنى" ، فيمكننا بناء نظرية بديلة ، تسمى نظرية الاحتمالات . هذه هي الطريقة التي تعمل الرياضيات. نبدأ بالتفكير التجريدي: الأرقام تشكل جبرًا مع عمليات الجمع والضرب ، ولكن يمكنك بناء جبر مماثل باستخدام عمليات الحد الأدنى والحد الأقصى. نحن نبني مفهوم القياس على جبر جديد ونكتشف أنه يفتح نظرة جديدة للعالم! على النقيض من نظرية الاحتمالات ، في مثل هذه النظرية ، يمكن بناء تدبيرين منسقين - الاحتمالية والضرورية ، وخلافا للاحتمال ، فهي في اتفاق جيد مع كل من عمليات الجمع بين الأحداث المتقاطعة. تم إنشاء هذا الاتجاه من قبل الأمريكي لطفي زاده ، وهو أذربيجاني الأصل ، وهو بمثابة الأساس المنطقي للمنطق الضبابي ويستخدم في أنظمة التعرف على الأنماط واتخاذ القرارات تلقائيًا.

لا يصدق ، ولكن صحيح!

الخاصية الأولى للتدابير تبدو تافهة ، لكنها مثيرة للاهتمام في عدم تناسقها. إذا كان قياس المجموعة الفرعية صفرًا ، فهذا لا يعني أنه فارغ! على سبيل المثال ، يمثل الخط مجموعة فرعية من النقاط على المستوى ، لكن مساحته (قياس) هي صفر. هناك أمثلة أكثر غرابة - كانتور ومجموعات كسورية ، ذات بنية معقدة ، تحتوي على عدد لا حصر له من النقاط ، "تشغل" منطقة أو حجم معين بصريًا ، ولكن مع ذلك لا يوجد لها مقياس صفري.

بعض الأشياء من الصفر قياس: خط على متن طائرة ، مجموعة جوليا متقطعة ، Menger الإسفنج كسورية.

أثناء إعداد هذا الرسم التوضيحي ، وجدت صورة رائعة لمجموعة من جوليا غير متصلة على خلفية شفافة بجودة عالية. بعد إدخالها في محرر المتجهات ، صادفت صعوبة مضحكة - كان من الصعب للغاية الدخول في هذه الصورة باستخدام الماوس لتحديدها. إنه "فضفاض" لدرجة أن احتمال الدخول إلى بكسل مملوء كان أقل بشكل ملحوظ من الدخول إلى خلفية شفافة. في مساحة الاحتمال ، قد توجد مجموعات فرعية ذات قياس صفر أيضًا ، لكن هذا لا يعني أن أحداث هذه المجموعات الفرعية مستحيلة. من المحاولات الرابعة إلى الخامسة ، لا يزال بإمكاني تحديد الصورة ، حيث يكون للبكسل حجم محدود. ولكن ماذا سيحدث إذا حصلت على مجموعة غير متماسكة حقيقية من جوليا بدقة لا نهائية؟

تخيل أنك تستخدم مولد رقم عشوائي للبرنامج ينتج عنه رقم حقيقي اعتباطي $$$0$ قبل $$$1$ . ما هو احتمال سقوط عدد؟ $$$0$ ؟ والأرقام $$$1/2$ او $$$e / \ pi$ ؟ في كل هذه الحالات ، سيكون الجواب - صفر! بدلاً من ذلك ، فإن أصغر رقم موجب متاح للكمبيوتر هو ما يسمى epsilon ، لأن الكمبيوتر يعمل بعدد محدود من المنازل العشرية. انتظر ، كما تقول ، ما معنى الصفر؟ نفس الأرقام ليست مستحيلة. دعنا نجري تجربة ، ونتيجة لذلك نحصل على بعض الأرقام المحددة ، وعندما نحصل عليها ، ثم "عن طريق البناء" لا يمكن أن يكون احتمال ظهورها صفرًا. هذا صحيح ، ولكن كم من الوقت يجب أن أنتظر حتى يسقط 0 بالضبط؟ ما لا نهاية تقريبا! والحقيقة هي أن الرقم الفردي ، مثل أي نقطة في مقطع ما ، له مقياس صفر واحتمال صفر صريح. فقط مقياس لشريحة مستمرة ، حتى صغير جداً ، غير صفري. لذلك نحن لا نتحدث عن الاحتمال ، ولكن عن الكثافة الاحتمالية ، والتي عند ضربها بمقياس محدد لمجموعة فرعية في مساحة الاحتمال ، ستعطي قيمة محددة - احتمال الوقوع في هذه المجموعة الفرعية. بالمناسبة ، اتضح أننا مولد الأرقام العشوائية المثالي بدقة لا حصر لها ، واحتمال الحصول على عدد عقلاني (وليس بعض الاسمنت ، ولكن أي) سيكون أيضًا صفرًا. إن إثبات أن الأرقام المنطقية تشكل مجموعة فرعية كثيفة ذات مقياس صفري لمجموعة الأرقام الحقيقية تسببت في الضوضاء في نهاية القرن التاسع عشر.

إذا أجرى شخص ما بصبر ألف تجربة باستخدام عملة معدنية وأخبرك بسعادة أنه حصل على "نسور" بأكبر عدد من "النسور" ، فيمكنك التعبير بأمان عن شكوك أو تهنئته على الحظ النادر. على الرغم من إلقاء عملة معدنية وعملية عشوائية منفصلة ، كما تتراكم الإحصائيات ، ستزداد قوة مساحة الاحتمال وقياس الحدث: "عدد" النسور "يتزامن مع عدد" ذيول "" سينخفض. يمكن أن يظهر ، باستخدام صيغة ستيرلينغ ، أن احتمال هذا الحدث "الأكثر احتمالًا" يميل إلى الصفر مع زيادة في عدد الاختبارات كما $$$1 / \ sqrt {\ pi n}$ . بالنسبة لمئات الممثلين ، هذا يزيد قليلاً عن خمسة بالمائة ، لعشرة آلاف - نصف فقط بالمائة. في مثل هذه الحالات ، يقول علماء الرياضيات: من شبه المؤكد أن عدد "النسور" لن يكون مساوياً لعدد "ذيول" . لا يهم كم يبدو غريباً ، ولكن "من شبه المؤكد" هو مصطلح رياضي دقيق ، وهذا يعني أن الحدث هو مكمل لمجموعة فرعية من مساحة الاحتمال صفر قياس. سنعود إلى هذه الاعتبارات في أحد الفصول التالية ، عندما نسأل أنفسنا السؤال: إلى أي مدى يمكن لكل واحد منا أن يعتبر أنفسنا طبيعيين.

التحقق من صدق عملة حقيقية

دعنا نعود إلى العملة وصدقها. التوفيق بين تعريف Kolmogorov للاحتمال تعريف التردد الخاص به (كتردد نسبي للأحداث التي تحدث) والهندسي (كجزء بسيط من "حجم" حدث ما في "حجم" الاحتمالات الكلي). وبالتالي ، فإن جزء من مساحة الخطوط البيضاء في الرسم البياني المحسوب لعملة معدنية تعكس احتمال السقوط من نفس الجانب الذي ألقينا به.

لكن المشكلة! مساحة كل شريط في الرسم التخطيطي لدينا هي لانهائية (إذا أخذنا في الاعتبار الربع بأكمله من طائرة الإحداثيات). ومع ذلك ، فإن الإضافة إلى المقياس ستتيح لنا أن نوضح بدقة أن هذا لا يمنع مساحات المناطق المظللة والبيضاء من التماثل. في شكل واضح ، معادلات منحنيات لدينا لديها الشكل$$$\omega = n/t$ . إذا كانت المنطقة تحت المنحنى $$ω = 1 / t يساوي$\omega = 1/t$$$S ، ثم بسبب خاصية الإضافة ، المنطقة تحت المنحنى$S$$$ω = n / t ستكون متساوية$\omega = n/t$$$$S_n = n S$ . بدوره ، بالنسبة للشرائح الفردية ، نحصل على: $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ .اتضح أن الفرق في المنطقة لا يعتمد على "عدد" القطع الزائد. هذا ليس شيئًا خاصًا بالنسبة للقطع الزائد ؛ يمكن استخلاص نفس الاستنتاج لأي منحنى النموذج$$y = n f ( x ) ، إذا كانت الوظيفة فقط$y = n f(x)$$$كان f قابلة للقياس. وإذا كان الأمر كذلك ، فبالنسبة لمنطقة التعريف بأكملها ، يكون الدخول إلى الجزء الأبيض من المخطط أو في الشكل المظلل أمرًا محتملًا بنفس الدرجة ، كما هو متوقع لعملة "صادقة". يبدو أن المنطق الذي قدمناه للتو بسيط بما فيه الكفاية ، ولكنه يعطي نتيجة عامة للغاية ، تنطبق على أي كميات مضافة. لقد سمح لنا المفهوم التجريدي للقياس بمقارنة الكميات التي لا نهاية لها فيما بينها ، بينما نبقى في إطار المنطق والحس السليم. التجريد جيد ، لكن يمكن القول أننا في الواقع لا نرمي العملات المعدنية بكل المقاييس الممكنة. كما أظهرت التجارب على كاميرا عالية السرعة ، تقع السرعات الزاوية في نطاقها$f$



$$20 إلى$20$$$40 لفة في الثانية الواحدة ، ومدة الرحلة من نصف إلى ثانية واحدة. يتم تمييز هذه المنطقة بواسطة مستطيل في المخطط. في ذلك ، تكون المساحة الكلية للخطوط البيضاء أكبر قليلاً من الخطوط البرتقالية ، ويمكننا أن نستنتج أن احتمال السقوط من نفس الجانب الذي كان أثناء الرمي سيكون$40$$$$50.6\%$ .

في عام 2007 ، نشرت مجموعة من Percy Deaconess et al من جامعة ستانفورد مقالة توفر تحليلًا تفصيليًا لعملية رمي العملة المعدنية. هناك وصف مفصل لميكانيكا القرص الطائر والدائر ، والذي لا يدور فقط ، ولكن أيضًا التدوير - محور الدوران نفسه يدور في الجو ، مع أنه من خلال إرم يدوي من موضع "النسر من أعلى" ، فإن احتمال سقوط "النسر" بمقدار مائة هو أكثر من النصف.

هل هو كثير أم قليلا؟ كم عدد التجارب التي تحتاجها لإحداث مثل هذا الاختلاف؟ مع تراكم البيانات التجريبية ، ينخفض ​​الخطأ المعياري للمتوسط ​​، الذي يعكس الخطأ الذي يمكن به حساب القيمة المتوسطة ، بما يتناسب مع الجذر التربيعي لعدد الاختبارات:$$σ μ = σ / √ن هنا$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ هو الانحراف المعياري للتوزيع المدروس. في حالتنا ، لتوزيع برنولي مع احتمال$\sigma$$$0.51 وهو يساوي$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ . لتحديد بثبات انحراف متوسط ​​المائة ، يجب أن يتجاوز هذا الانحراف $$3 الانحرافات القياسية. وبالتالي ، يمكننا تقدير عدد التجارب:$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

في كثير من الأحيان تحتاج إلى قلب عملة معدنية لتلاحظ التحديد المسبق الميكانيكي للنتيجة. لتوضيح المعنى المقصود ، سأقدم مثالاً على مئتي اختبار لـ "عملات" مثالية وغير كاملة قليلاً أجريت من أجل حساب احتمال فقدان النسر ، على سبيل المثال. كل اختبار يتكون من$$40000 إرم. إن الكلمات "coin" و "tossing" هي علامات اقتباس ، لأنه في الواقع ، لم يتم استخدام عملة معدنية ، ولكن منشئ أرقام عشوائي يطيع توزيع Bernoulli.$40000$

قم بتجارب القذف بعملة مثالية وعالية النقص قليلاً من أجل إصلاح النقص.

وينظر إلى أنه فقط بعد$$20،000 اختبار من "سحابة" من القيم يعني لوحظ تبدأ منفصلة بشكل واضح. حسنًا ، للاستخدام المحلي ، يمكننا أن نفترض أن العملة هي مولد جيد لاختيار عشوائي من خيارين محتملين بنفس القدر.$20000$

قانون السياحة

يكشف تكافؤ الاحتمال الهندسي وتردد الاحتمالات عن سر وجود قانون واحد للخسارة ، معروف لدى السياح والجيولوجيين وجميع الذين يستخدمون الخرائط الطبوغرافية:

غالبًا ما يكون المكان الذي يذهب إليه السائح إما على حظيرة الخريطة أو على حافة الورقة.

لنفترض أننا مهتمون في الغالب بالأشياء الموجودة في جميع أجزاء الخريطة. لكننا نادراً ما نرغب في كائنات ذات قياس صفري - بيت القصيد من استخدام الخريطة هو مسح المناطق المحيطة بالكائن ، أي منطقة محددة. اسمحوا جزء صغير يكون كافيا بالنسبة لنا$$α من منطقة الخريطة بأكملها$\alpha$$$S لمعرفة كيفية الوصول إلى الكائن. لذلك ، إذا كان الكائن يقترب من الانحناء أو الحافة في بعض المسافة الحرجة$S$$$د ، ونحن sochtom القانون الرحال تشغيل. ستمنحنا حصة المناطق الحدودية في المساحة الكلية للخريطة الفرصة لتجربة هذا القانون المنطقي على أنفسنا. هذا ما تبدو عليه الأجزاء غير السارة بالخريطة$د$$$α = 0.5 ٪ وفي ثني واحد.$\alpha=0.5\%$

الرمادي يشير إلى المناطق "السيئة". يظهر بشكل منفصل جزء من منطقة نصف نقطة للبطاقة عرض 40 سم، والتي يبلغ قطرها قليلا أكبر من 3 سم.

وبالنسبة لبطاقة مربع$$$d = \sqrt{\alpha S}$ . سوف شرائط غير سارة لها مساحة $$$d \sqrt{S} = S\sqrt{\alpha}$ .سيتم وضع أربعة خطوط ، عموديتان واثنتان أفقية ، على الحافة ، أي منحنى إضافي ، أفقي أو عمودي ، سيضيف شريطًا آخر. في الوقت نفسه ، تضيف الشرائط المتقاطعة مربعات إضافية بمساحة$$$d^2 = \alpha S$ . عن طريق طي البطاقة بحيث اتضح $$$ن$ أفقي و $$$م دولا$ الانحناءات الرأسية ، نحصل على مساحة إجمالية للمنطقة غير السارة تساوي: $$$S (n + 2) \ sqrt {\ alpha} + S (m + 2) \ sqrt {\ alpha} -S (n + 2) (m + 2) \ alpha$ . نأخذها إلى منطقة الخريطة بأكملها ، نحصل على حصة غير سارة من إجمالي المساحة:

$$

$$p = (n + m + 4) \ sqrt {\ alpha} - (n + 2) (m + 2) \ alpha.$$

يوضح الشكل المناطق التي تتجاوز فيها هذه النسبة $$$50 \٪$ لمختلف القيم $$$\ alpha$ .

المناطق التي يزداد فيها احتمال وجودها في حظيرة الخريطة أو على أطرافها. تشير الأرقام إلى جزء مساحة الحي المجاور من منطقة الخريطة بأكملها.

اتضح أن البطاقة المطوية في نصفين يمكن اعتبارها بالفعل غير نزيهة بالنسبة للسائح. في معظم الأحيان ، تحتوي البطاقات على ثلاثة طيات رأسية وثلاثية أفقية ، مما يعطي احتمال الوفاء بقانون الثبات مع احتمال حوالي $$$60 \٪$ في $$$\ alpha = 0.5 \٪$

من أين تأتي الفرصة؟

في محلات بيع التذكارات ، يمكنك العثور على بندولات مغناطيسية "لاختيار الرغبات". هم ، أيضا ، مولدات عشوائية ميكانيكية وتسمى أحيانا عن طريق الخطأ "البندول الفوضوي". انطلاقًا من بعض المواقف والسرعة المبدئية ، يؤدي البندول سلسلة من التذبذبات "غير المتوقعة" وتوقف أخيرًا في أحد القطاعات. ومع ذلك ، فإن التقلبات هنا لا يمكن التنبؤ بها ، فهي ببساطة حساسة للغاية للظروف الأولية. لكل قطاع يمكن أن يتوقف فيه البندول ، توجد منطقة جذب في مساحة السرعة الإحداثية. هذه هي مجموعة من هذه الشروط الأولية التي بموجبها سوف يجذب البندول بالضرورة إلى نقطة معينة في القطاع المشار إليه. تسمى نقطة توقف البندول بجاذب - نقطة جذب. في حالة البندول من الصورة ، تكون مساحة الإحداثيات والسرعات ثلاثية الأبعاد ، وبالتالي ليس من السهل إظهار منطقة الجذب. لكن إذا قصرنا أنفسنا على قطاعين فقط وقللنا المشكلة إلى أحادية البعد (مثل هذا البندول يسمى مذبذب Duffing) ، فإن مساحة القيم الأولية ستتحول إلى مستوى ، بحيث يمكن رؤية مناطق الجذب. تبدو مثل رمز Yin-Yang معقدة ، تتحول بسرعة إلى شرائح ضيقة تفصل بين مناطق الجذب.

مجالات الجذب لجاذبي البندول أحادي الأبعاد للرغبات - مذبذب Duffing.

كما هو الحال في العملة المعدنية ، حيث نغير قليلاً من الشروط الأولية ، ننتقل من جاذب لآخر. النرد والروليت يعملون بنفس الطريقة ، لكنهم ليسوا مولدات عشوائية. هذه ليست أنظمة فوضوية حقًا ويمكن حساب سلوكها بدقة.

ولكن ما هي الفرصة الحقيقية؟ مثال جيد على نظام ستوكاستيك الحقيقي هو ظهور السيارات على الطريق. الناس لا يوافقون ، لا ينسقون خططهم ، كل عنصر من عناصر المجموعة خارج الطريق يعمل بشكل مستقل. وعلى الرغم من وجود أنماط معينة في سلوك الناس - ساعات الذروة في الصباح والمساء ، والطرق الفارغة في الليل ، وما إلى ذلك ، ليس لدينا ولن يكون لدينا معلومات كافية عن كل مشارك في الحركة للتنبؤ بظهور أي منهم. كما أن ميكانيكا الجسيمات الأولية على المستوى الكمي ، وتحلل الذرات غير المستقرة ، والتغيرات في الكود الجيني ، على الأرجح ، الزلازل وأسعار الأسهم في البورصة هي مؤشرات عشوائية. الشيء الوحيد المتبقي للباحث هو اعتبارها متغيرات عشوائية ووصفها من حيث نظرية الاحتمالات.

ولكن هناك مصدر آخر للفرصة - الفوضى الديناميكية . تختلف الأنظمة الفوضوية عن الأنظمة العشوائية حيث يتم وصفها بالمعادلات الدقيقة والمعلمات التي لا تحتوي على العشوائية. ومع ذلك ، فإن سلوكهم ليس مجرد تعقيد ، ولكنه فوضوي وغير متوقع حقًا. إذا بدأنا في تأرجح البندول من الرغبات ، بعناية فائقة ، مع التردد والسعة التي تسيطر عليها بدقة ، سنجد أنه لا يمكن حساب حركاتها على نحو سلس لفترة طويلة. لن تسمح لنا أي خوارزميات على أجهزة كمبيوتر دقيقة بشكل تعسفي بحساب السلوك الدقيق للبندول لمستقبل بعيد بشكل تعسفي. لن يتوقف عند أي قطاع ، لكنه سيحرك بسلاسة ، لكنه لن يعود أبدًا إلى نفس النقطة في مساحة سرعة الإحداثيات مرتين. مثال آخر على نظام فوضوي بسيط للغاية هو كرة مثالية ترتد في حقل الجاذبية على طاولة مثالية مع نبع. أظهرت معادلات لورنتز البسيطة نسبياً أنه لا يمكننا أبدًا التنبؤ بالطقس لأكثر من أسبوعين - وهذا أيضًا نظام فوضوي.

كانت نظرية الفوضى الديناميكية قادرة على شرح طبيعة عدم القدرة على التنبؤ. كان للبندول البسيط أحادي البعد للرغبات ، الذي درسناه ، نقطتان ثابتتان ثابتتان - جاذبيتان ، وأخرى غير مستقرة ، يحاول النظام الخروج منها ، تظهره دائرة بيضاء. في الوضع الفوضوي ، بدلاً من مجموعة من عوامل الجذب ، يظهر عدد غير محدود من المسارات الثابتة غير المستقرة في النظام. هذه المجموعة لا حصر لها ، ولكنها ذات قياس صفري ، وهي عبارة عن بنية مفككة معقدة للغاية. مرة واحدة على واحدة من هذه المسارات ، من حيث المبدأ فإنه من المستحيل متابعتها باستخدام أي خوارزميات محدودة. ولكن الأكثر إثارة للدهشة ، اتضح أن هذا العدد غير المحدود من المسارات غير المستقرة في حد ذاته جذابة! 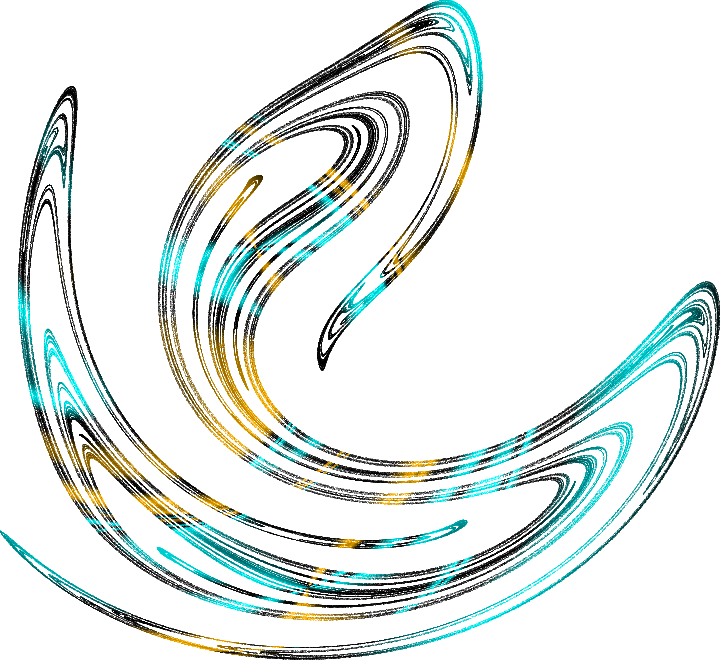ينتقل النظام الفوضوي بشكل مستمر من محيط مسار غير مستقر إلى آخر ، في حين يبقى كل ذلك في حدود هذا الجاذب الغريب. لذلك تسمى هذه المجموعات: جاذبي غريب . هذه هي الطريقة التي يبدو بها قسم من جاذب غريب عن البندول من الرغبات ، تخضع لتذبذبات التوافقي ، جميلة رائعة. يمكن وصف هذا الكائن من أجل البندول أحادي البعد في الفضاء ثلاثي الأبعاد (الإحداثيات والسرعة ومرحلة التذبذب القسري). إذا قمت بقص جاذب في هذا الفضاء بواسطة طائرة ، يمكنك أن ترى هيكلها ، وهذا ما يسمى قسم Poincare . كل نقطة هنا هي تتبع للمسار ، ولون النقاط يعكس السرعة النسبية التي تنتشر بها المسارات من بعضها البعض. وهنا اثنين من جاذبي غريب جميل:


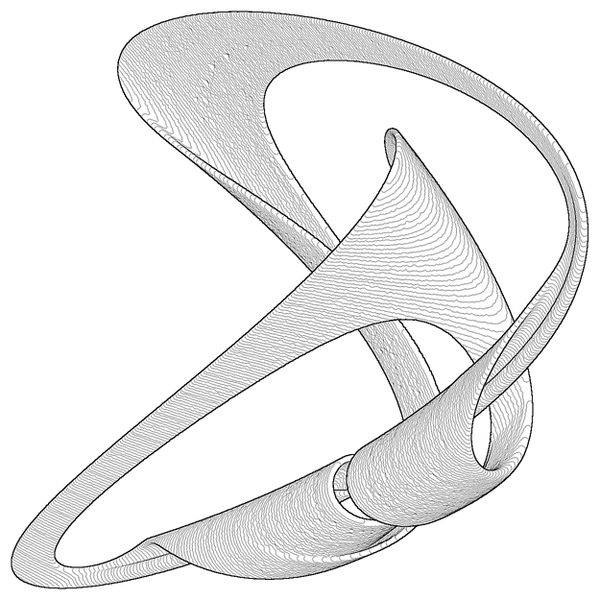إلى اليسار: قسم Poincare لمسار كرة كذاب على طاولة محملة بنابض. العديد من النقاط تنتمي إلى سطح الكرة المقابلة لقانون الحفاظ على الطاقة. إلى اليمين: منطقة حجرية تحيط بجاذب غريب يولد أثناء الاهتزازات القسرية لصفيحة سميكة.

تتيح لك نعومة المسار الفوضوي النظر قليلاً في المستقبل. هذا ما يفسر ملاحظة واحدة مزعجة: من ناحية ، لا يمكن للمتنبئين بالطقس في بعض الأحيان التنبؤ بثقة بالطقس لمدة أسبوع ، ولكن من ناحية أخرى ، إذا قلت إن الطقس سيكون غدًا كما هو الحال اليوم ، فلن يتم إخطارك في ثلاث حالات من أصل أربع حالات . بشكل عام ، النكات المتعلقة بتنبؤات الطقس غير عادلة ويجب علينا أن نشيد بالفكر الإنساني والمثابرة ، مما جعل من الممكن التنبؤ بالطقس على مستوى حديث!

الفوضى الديناميكية معقدة وجميلة للغاية كنظرية ، وتؤدي إلى ظهور صور للأناقة المذهلة ، ولكنها قد تكون مفيدة أيضًا. على سبيل المثال ، الخوارزميات التي يتم بها إنشاء أرقام عشوائية في أجهزة الكمبيوتر هي أيضًا حتمية. على سبيل المثال في هذا الكتاب ، استخدمت مولد الأرقام العشوائية المزيفة التي لم تبدأ عملية الاستوكاستك الحقيقية (تحلل ألفا ، أو عد السيارات على الطريق) ، لكنني قمت بحساب الرقم "العشوائي" التالي بناءً على الأرقام السابقة التي تلقاها سابقًا.

من العملات إلى الفراشات ومصيرها

تؤدي الملاحظات حول كيفية نمو الانحرافات الصغيرة إلى تغييرات عالمية في النظام إلى التفكير في "تأثير الفراشة". واسمحوا لي أن أذكرك بأن هذا التأثير يعني سلسلة من العواقب الدرامية بعيدة المدى من بعض الأحداث غير المهمة ، للوهلة الأولى. بعد أن سحقها باحثون من الماضي ، أدت الفراشة في قصة راي برادبري القصيرة "وضرب الرعد" إلى إعادة هيكلة جذرية للمستقبل. وإحدى محاضراته ، إدوارد لورينز ، مبتكر نظرية الفوضى الديناميكية ، بعنوان: "هل يمكن لرفرفة جناح الفراشة في البرازيل أن تسبب إعصارًا في تكساس؟"

نشير ضمنيًا إلى هذا التأثير ، معربًا عن أسفه قائلاً: "لو لم أقف في الزاوية ، فكل شيء كان سيختلف!" ، "لو لم يستقل هذا القطار ، لما وقعت كارثة!" أو "بسبب هذه التفاهات ، تشاجروا ويفترقوا !!" لكننا نرى أن عالمًا كميًا استوكاستيًا حقًا وساعات ذرية فائقة الدقة تتعايش في العالم ، وأنظمة هاملتون مستقرة في عالم النجوم والمجرات وفوضى حلقات زحل أو حلقات كويبر ، والحركة الحرارية للجزيئات ، والدقة المدهشة لتشغيل الأنظمة البيولوجية أو آليات السيارات. لا ، لا يؤدي رفرف جناح الفراشة إلى حدوث أعاصير ، ولكنه يختفي بدون أثر ، مما يؤدي إلى سلسلة من الدوامات التي تنقل الطاقة والمعلومات إلى دوامات أصغر حجمًا إلى أن تختفي كل من الطاقة والمعلومات في فوضى التقلبات. يجب أن يكون مفهوما بوضوح أن الانحرافات الصغيرة تؤدي إلى إعادة تنظيم أساسية للنظام فقط إذا كان غير مستقر أو إذا كان النظام على وشك التشعب أو الكارثة - هذا ما يطلق عليه إعادة الهيكلة العالمية في سلوك النظام مع تغييرات صغيرة في المعلمات في لغة الرياضيات. والتشعبات تشكل دائمًا مجموعات من الصفر قياس في مساحة المعلمة - هذه هي النقاط أو الحدود. لا تؤدي الاضطرابات الصغيرة إلى كوارث في كل مكان تقريبًا (وهذا هو أيضًا مصطلح دقيق يعني "في كل مكان ، باستثناء مجموعة من التدبير الصفري") ، ونادراً ما تتم ملاحظة حالات غير مستقرة في الطبيعة دون اجتياز "اختبار الزمن".

إذا انفصل الزوجان "بسبب الهراء" ، فقد كان مقدراً لها أن تنفجر في أي حال ، فهي غير مستقرة. يمر الأزواج المستقرون بالحروب والمجاعات ، ثم في بعض الأحيان ينفجرون ، ولكن ليس بسبب التافهات ، ولكن نتيجة للتغيرات العميقة التي يمكن أن تحدث للشخص خلال حياته. في سلسلة الأحداث التي أدت إلى تعطل القطار ، ليس من السهل تحديد حدث رئيسي (خطأ محدد أو حادث مميت) ، وعلى الأرجح ، المفتاح ليس حدثًا ، ولكنه انتهاك منهجي للقواعد ، مما يؤدي بالنظام إلى حالة غير مستقرة. إذا كان هناك الكثير من المعلمات في النظام ، وبعضها عشوائي ، وحياتنا مبنية على هذا النحو ، فإن المعلومات في مثل هذا النظام تميل إلى الضياع ، ولن يكون من الممكن استعادة في أي لحظة بالضبط في حياتنا "كل شيء خاطئ". لا تعذب نفسك مع الأسف لما حدث ، لكن ألقِ نظرة فاحصة على ما يحدث لك الآن ، حتى لا تفوت فرصة التشعب الحقيقية.

في هذا الصدد ، يمكننا أن نتذكر واحدة من قوانين المورفولوجيا ، ودعا قانون الاستعادة من قبل Dreisen معين:

وقت تحسين الوضع يتناسب عكسيا مع وقت تدهوره.

يتم تقديم الملاحظة التالية كمثال: يستغرق غراء الإناء وقتًا أطول من كسره. يصف هذا القانون بشكل مدهش بدقة العلاقة بين المعدلات المميزة لعملية استرخاء نظام مستقر ، والتي يمكن وصفها بواسطة قانون الأس المتناقص. $$$e ^ {- \ lambda t}$ ومعدل تطور العملية الكارثية في نظام غير مستقر ، في التقريب الخطي - النمو الهائل لاضطراب صغير $$$e ^ {\ lambda t}$ . هذه السرعات تتناسب عكسيا مع بعضها البعض. مثال المزهرية ، ليس الاسترخاء - الانتقال إلى الحالة الأكثر احتمالا. إنها أقرب إلى عملية أخرى - للتنظيم الذاتي ، هذه العملية ، كتقريب أولي ، موصوفة في القانون اللوجستي وأقرب إلى الاسترخاء من سرعة إلى كارثة.

العمليات غير الثابتة النموذجية: الكوارث ، الاسترخاء والتنظيم الذاتي ، لها نفس الوقت المميز.

$$

$$* * *$$

أحيانًا ، أثناء المشي في الثلج ، أدهشني أن ندفة الثلج تسقط على أنفي. أنا مندهش أن احتمال هذا الحدث كان ضئيلاً. انطلاقًا من ذلك ، وُلدت عالياً في السماء فوق المحيط الهادئ ، محاطة بدائرة في التيارات المضطربة غير المعتادة في السحابة ، وسقطت باستمرار في الاتجاه ... للوصول إلى طرف أنفي! وما هو المسار المذهل الذي تسافر به الفوتونات من نجم بعيد؟ لعشرات الآلاف من السنين سارعوا عبر الكون ، لم يبتلعهم الغبار ، ولم يقابلوا كويكبًا! لقد ولدوا في العالم الكمومي لنجم بعيد ، وأنهىوا رحلتهم في العالم الكمومي لبروتين الأوبسين على شبكية العين في عيني. لا يوجد أي معنى حتى عند التفكير في احتمال هذا الحدث ، فهو صفر ، لكن هذا الحدث يحدث ، وأرى ضوء وميض النجم. من الواضح الآن أن هذا كله لأن منطقة أنفي وحتى الجزيئات لها مقياس غير صفري ، لكنها ما زالت مدهشة: ما كان من المؤكد أنه لا ينبغي أن يحدث قد حدث!

دع الفلاسفة يجادلون حول المصير المحدد سلفًا أو العرضي أو حقيقة أو شبح معرفتنا بالطبيعة. أحث القارئ على النظر إلى العالم من ذروة التجريدات الرياضية والاعجاب بجماله واتساقه.