مقدمة
لقد أنشأنا شفرة فيريلوج توليفية لحساب جذر مكعب عدد صحيح من عدد صحيح عبر خوارزمية البحث الثنائية. تم اختبار هذا الرمز على لوحة Cyclone IV FPGA. هنا يمكنك أن تقرأ عن التنفيذ وتفهم كيف تعمل الأشياء.
رابط جيثب:
مكعب الجذرما هو الجذر مكعب؟
جذر المكعب لرقم
y هو رقم
x بحيث
عرض $$ $$ x ^ 3 = عرض $$ $
أمثلة:
عرض $$ $$ \ sqrt [3] {8} = 2 \\ \ sqrt [3] {27} = 3 \\ \ sqrt [3] {64} = 4 $$ عرض $$
لذلك ، في تنفيذ لدينا نستخدم
الجذر عدد صحيح مكعب .
هذا يعني أن جذر مكعب رقم صحيح
x هو رقم صحيح آخر بحيث:
عرض $$ $$ a ^ 3 \ leqslant x، \\ (a + 1) ^ 3 \ geqslant x $$ عرض $$
أمثلة:
عرض $$ $$ \ sqrt [3] {26} = 2 \\ \ sqrt [3] {28} = 3 \\ \ sqrt [3] {63} = 3 \\ \ sqrt [3] {65} = 4 $$ عرض $$
المنطق الرئيسي
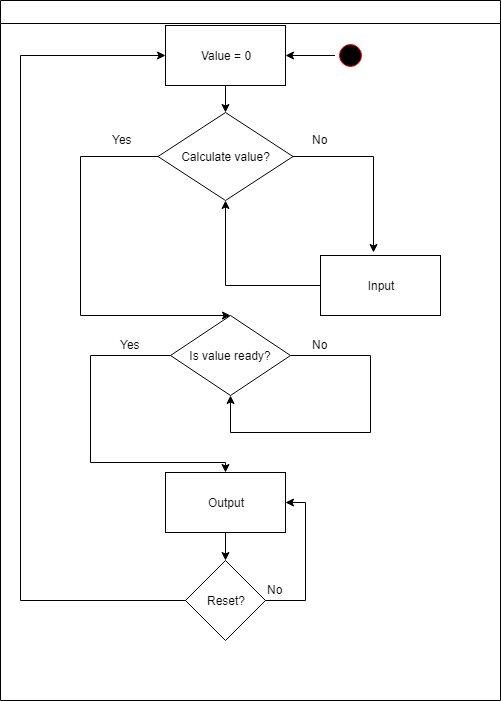
الوحدة الرئيسية هي المسؤولة عن جميع الإجراءات مع عدد أثناء الإدخال.
لديها 4 إجراءات محتملة:
- مضاعفة الزيادة بنسبة 10
- قسمة الزيادة على 10 (الزيادة دائما لا تقل عن 1)
- زيادة عدد
- انخفاض عدد
الوحدة الرئيسيةmodule cube_root( input inc, input sub, input next, input prev, input enter, input clk, output wire [7:0] leds, output wire [7:0] control ); reg signed [31:0] exit; wire ready; wire [31:0] res; reg zero = 0; // input // reg inc1 = 0; reg next1 = 0; reg prev1 = 0; reg sub1 = 0; reg enter1 = 0; reg [31:0] decimal = 1; ////////// reg [31:0] to_display; display_bcd display( .clk(clk), .value(ready == 0 ? exit : res), .control(control), .leds(leds) ); calculate calc( .clk(clk), .ready_to_calc(~enter), .num(exit), .ready(ready), .res(res) ); always @(posedge clk) begin if (enter == 1) begin if ((inc1 == 1'b0) && (~inc == 1'b1)) begin exit = exit + decimal; end inc1 = ~inc; if ((sub1 == 1'b0) && (~sub == 1'b1)) begin if (exit > 0) begin exit = exit - decimal; end end sub1 = ~sub; if ((next1 == 1'b0) && (~next == 1'b1)) begin decimal = decimal * 10; end next1 = ~next; if ((prev1 == 1'b0) && (~prev == 1'b1)) begin if (decimal >= 1 && decimal <= 9) begin decimal = 1; end else begin decimal = decimal / 10; end end prev1 = ~prev; end else begin if (ready == 1'b1) begin exit = 0; decimal = 1; end end end endmodule
في الوحدة النمطية الرئيسية
cube_root هناك أيضًا وحدتان أخريان:
حساب و
display_bcd . أول واحد يقوم بجميع العمليات الحسابية المطلوبة ، في حين أن الوحدة الثانية هي المسؤولة عن عرض قيم المدخلات والمخرجات أثناء تنفيذ البرنامج.
الآن ، دعونا نفهم كيف تعمل.
حساب الوحدة
تستخدم وحدة الحساب خوارزمية بحث ثنائية. وعندما يتم إجراء جميع العمليات الحسابية ، فإنه يقوم بتعيين متغير
جاهز على 1. إنها إشارة لوحدة العرض لإخراج الإجابة.
حساب الوحدة module calculate( input clk, input ready_to_calc, input [31:0] num, output reg ready, output [31:0] res ); integer mid; integer start; integer final; integer counter; assign res = mid; always @(posedge clk) begin if (ready_to_calc == 1) begin if (ready == 0) begin mid = (start + final )/2; if ((mid*mid*mid) > num) begin final = mid; end else begin start = mid; end if (counter == 27) begin ready = 1; counter = 0; end else begin counter = counter + 1; end end end else begin final = 465; start = 0; ready = 0; counter = 0; end end endmodule
لماذا هذه الوحدة تفعل بالضبط 27 التكرار؟- الحد الأقصى لعدد المدخلات هو 99999999. لذلك ، أقصى عدد ممكن من التكرارات هو
$ inline $ \ log_2 99999999 = 26.575424745 \ approx 27 $ $ inline $
لماذا يتم تهيئة الحد الأعلى للبحث الثنائي بواسطة 465؟- لأنه أقصى عدد يمكن أن نحصل عليه نتيجة لذلك.
$ inline $ \ sqrt [3] {99999999} \ approx 464 $ inline $
وحدة العرض
هذه الوحدة هي المسؤولة عن الأداء. يستخدم ثمانية شاشات عرض من ثمانية شرائح ويتم معالجتها بواسطة 16 دبابيس. عندما تكون "8 دبابيس" "مسئولة" عن المصابيح المعينة على الشاشة بينما تكون 8 دبابيس أخرى عبارة عن قطاعات تحكم ، فإنها تمثل أرقامًا مميزة.
لذا ، فإننا نمرر قيمة عدد صحيح نريد أن نعرضها على هذه الوحدة. بعد ذلك ، تقوم بتمرير هذه القيمة إلى الوحدة النمطية
Binary_to_BCD التي تحول الرقم الثنائي إلى عشري ترميز ثنائي باستخدام
خوارزمية Dabble مزدوجة . بعد ذلك ، تصبح القيمة المحولة سهلة العرض.
وحدة العرض module display_bcd ( input clk, input [31:0] value, output [7:0] control, output [7:0] leds ); bcd_convert #(32, 8) bcd_convert( .i_Clock(clk), .i_Binary(value_temp), .i_Start(1'b1), .o_BCD(bcd_number), .o_DV(bcd_ready) ); integer delay = 0; integer final_bcd; reg [2:0] ctrl = 0; reg [4:0] digit; wire bcd_ready; wire [31:0] bcd_number; wire [31:0] digits; assign digits = final_bcd; wire [31:0] value_temp; assign value_temp = value; assign control = ~(1 << ctrl); assign leds = ~ (digit == 0 ? 8'b00111111 : (digit == 1 ? 8'b00000110 : (digit == 2 ? 8'b01011011 : (digit == 3 ? 8'b01001111 : (digit == 4 ? 8'b01100110 : (digit == 5 ? 8'b01101101 : (digit == 6 ? 8'b01111101 : (digit == 7 ? 8'b00000111 : (digit == 8 ? 8'b01111111 : (digit == 9 ? 8'b01101111 : 8'b00000000)))))))))); always @(posedge clk) begin if (bcd_ready) final_bcd = bcd_number; case(ctrl) 0: digit = digits[3:0]; 1: digit = digits[31:4] ? digits[7:4] : 10; 2: digit = digits[31:8] ? digits[11:8] : 10; 3: digit = digits[31:12] ? digits[15:12] : 10; 4: digit = digits[31:16] ? digits[19:16] : 10; 5: digit = digits[31:20] ? digits[23:20] : 10; 6: digit = digits[31:24] ? digits[27:24] : 10; 7: digit = digits[31:28] ? digits[31:28] : 10; endcase delay = delay + 1; if (delay == 10000) ctrl = ctrl + 1; end endmodule
تحويل BCD module bcd_convert #(parameter INPUT_WIDTH, parameter DECIMAL_DIGITS) ( input i_Clock, input [INPUT_WIDTH-1:0] i_Binary, input i_Start, output [DECIMAL_DIGITS*4-1:0] o_BCD, output o_DV ); parameter s_IDLE = 3'b000; parameter s_SHIFT = 3'b001; parameter s_CHECK_SHIFT_INDEX = 3'b010; parameter s_ADD = 3'b011; parameter s_CHECK_DIGIT_INDEX = 3'b100; parameter s_BCD_DONE = 3'b101; reg [2:0] r_SM_Main = s_IDLE; // The vector that contains the output BCD reg [DECIMAL_DIGITS*4-1:0] r_BCD = 0; // The vector that contains the input binary value being shifted. reg [INPUT_WIDTH-1:0] r_Binary = 0; // Keeps track of which Decimal Digit we are indexing reg [DECIMAL_DIGITS-1:0] r_Digit_Index = 0; // Keeps track of which loop iteration we are on. // Number of loops performed = INPUT_WIDTH reg [7:0] r_Loop_Count = 0; wire [3:0] w_BCD_Digit; reg r_DV = 1'b0; always @(posedge i_Clock) begin case (r_SM_Main) // Stay in this state until i_Start comes along s_IDLE : begin r_DV <= 1'b0; if (i_Start == 1'b1) begin r_Binary <= i_Binary; r_SM_Main <= s_SHIFT; r_BCD <= 0; end else r_SM_Main <= s_IDLE; end // Always shift the BCD Vector until we have shifted all bits through // Shift the most significant bit of r_Binary into r_BCD lowest bit. s_SHIFT : begin r_BCD <= r_BCD << 1; r_BCD[0] <= r_Binary[INPUT_WIDTH-1]; r_Binary <= r_Binary << 1; r_SM_Main <= s_CHECK_SHIFT_INDEX; end // Check if we are done with shifting in r_Binary vector s_CHECK_SHIFT_INDEX : begin if (r_Loop_Count == INPUT_WIDTH-1) begin r_Loop_Count <= 0; r_SM_Main <= s_BCD_DONE; end else begin r_Loop_Count <= r_Loop_Count + 1; r_SM_Main <= s_ADD; end end // Break down each BCD Digit individually. Check them one-by-one to // see if they are greater than 4. If they are, increment by 3. // Put the result back into r_BCD Vector. s_ADD : begin if (w_BCD_Digit > 4) begin r_BCD[(r_Digit_Index*4)+:4] <= w_BCD_Digit + 3; end r_SM_Main <= s_CHECK_DIGIT_INDEX; end // Check if we are done incrementing all of the BCD Digits s_CHECK_DIGIT_INDEX : begin if (r_Digit_Index == DECIMAL_DIGITS-1) begin r_Digit_Index <= 0; r_SM_Main <= s_SHIFT; end else begin r_Digit_Index <= r_Digit_Index + 1; r_SM_Main <= s_ADD; end end s_BCD_DONE : begin r_DV <= 1'b1; r_SM_Main <= s_IDLE; end default : r_SM_Main <= s_IDLE; endcase end // always @ (posedge i_Clock) assign w_BCD_Digit = r_BCD[r_Digit_Index*4 +: 4]; assign o_BCD = r_BCD; assign o_DV = r_DV; endmodule // Binary_to_BCD
المؤلفون: تيورين ليونيد ، تيخونوف نيكيتا.