الرياضيات في Gamedev بسيطة. المصفوفات والتحولات أفيني

مرحبا بالجميع! اسمي Grisha وأنا مؤسس CGDevs. اليوم أريد أن أستمر في موضوع الرياضيات في لعبة ديف. في مقال سابق ، أظهرنا أمثلة أساسية لاستخدام المتجهات والتكاملات في مشاريع الوحدة ، والآن دعونا نتحدث عن المصفوفات وتحولات القرب. إذا كنت ضليعا في مصفوفة الحساب ؛ أنت تعرف ماهية TRS وكيفية التعامل معها ؛ ما هو تحول صاحب المنزل - ربما لن تجد شيئًا جديدًا لنفسك. سنتحدث في سياق الرسومات ثلاثية الأبعاد. إذا كنت مهتما بهذا الموضوع - مرحبا بكم في القط.



لنبدأ بواحد من أهم المفاهيم في سياق المقالة - تحويلات الألفة . إن تحولات الأفين هي ، في جوهرها ، تحول نظام الإحداثيات (أو الفضاء) عن طريق ضرب المتجه بمصفوفة خاصة. على سبيل المثال ، التحولات مثل الحركة ، الدوران ، التدرج ، الانعكاس ، إلخ. الخصائص الرئيسية للتحولات الذكرية هي أنك تبقى في نفس المكان (من المستحيل أن تصنع متجهًا ثنائي الأبعاد من ثنائي الأبعاد) وأنه إذا كانت الخطوط متقاطعة / متوازية / تم شطبها قبل التحويل ، ثم سيتم الاحتفاظ بهذه الخاصية بعد التحويل. بالإضافة إلى ذلك ، لديهم الكثير من الخصائص الرياضية التي تتطلب معرفة نظرية المجموعات والمجموعات والجبر الخطي ، مما يجعل العمل معهم أسهل.

مصفوفة TRS

المفهوم المهم الثاني في رسومات الحاسوب هو مصفوفة TRS . باستخدامه ، يمكنك وصف العمليات الأكثر شيوعًا المستخدمة عند العمل باستخدام رسومات الكمبيوتر. مصفوفة TRS هي تركيبة من ثلاث مصفوفات تحويل. مصفوفات الإزاحة (الترجمة) ، الدوران على كل محور (الدوران) والقياس (مقياس).
انها تبدو مثل هذا.



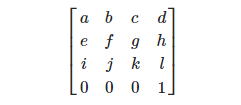
حيث:
الخطوة هي t = Vector3 جديدة (د ، ح ، ل).
القياس - s = new Vector3 (Vector3 (a ، e ، i) .magnitude ، Vector3 (b، f، j) .magnitude، Vector3 (c، g، k) .magnitude)؛

التناوب هو مصفوفة من الشكل:



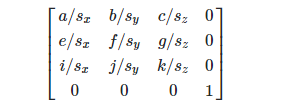
الآن دعنا نذهب قليلاً في سياق الوحدة. بادئ ذي بدء ، مصفوفة TRS هي شيء مريح للغاية ، ولكن لا ينبغي استخدامها في كل مكان. نظرًا لأن الإشارة البسيطة لموضع أو إضافة المتجهات في الوحدة ستعمل بشكل أسرع ، ولكن في العديد من الخوارزميات الرياضية ، تكون المصفوفات أكثر ملاءمةً من المتجهات عدة مرات. يتم تطبيق وظيفة TRS في الوحدة إلى حد كبير في فئة Matrix4x4 ، لكنها ليست ملائمة من وجهة نظر التطبيق. نظرًا لأنه ، بالإضافة إلى تطبيق المصفوفة من خلال الضرب ، يمكنه عمومًا تخزين المعلومات حول اتجاه الكائن ، وبالنسبة لبعض التحويلات ، أود أن أكون قادرًا على حساب ليس فقط الموضع ، ولكن أيضًا تغيير اتجاه الكائن ككل (على سبيل المثال ، الانعكاس الذي لا يتم تطبيقه في الوحدة)

يتم توفير جميع الأمثلة أدناه لنظام الإحداثيات المحلي (يُعتبر أصل GameObject هو أصل الإحداثيات ، حيث يقع الكائن داخلها. إذا كان الكائن هو جذر التسلسل الهرمي في الوحدة ، يكون الأصل هو العالم (0،0،0)).

نظرًا لاستخدام مصفوفة TRS ، يمكننا وصف موضع كائن ما في الفضاء ، نحتاج إلى تحلل من TRS إلى القيم المحددة للموضع ، الدوران ومقياس الوحدة. للقيام بذلك ، يمكنك كتابة طرق التمديد للفئة Matrix4x4


بالإضافة إلى ذلك ، من أجل العمل المريح ، يمكنك تنفيذ بعض ملحقات فئة التحويل للعمل مع TRS فيه.


على هذا ، فإن مزايا الوحدة تنتهي ، حيث أن المصفوفات في الوحدة ضعيفة جدًا في العملية. تتطلب العديد من الخوارزميات حساب مصفوفة ، والذي لا يتم تنفيذه في الوحدة حتى في العمليات الأساسية تمامًا ، مثل إضافة المصفوفات ومصفوفات الضرب بواسطة العددية. بالإضافة إلى ذلك ، نظرًا لخصوصية تنفيذ المتجهات في Unity3d ، هناك أيضًا عدد من الإزعاج المرتبط بحقيقة أنه يمكنك إنشاء ناقل 4 × 4 ، ولكن لا يمكنك إخراج 1 × 4 من المربع. نظرًا لأننا سنتحدث أكثر عن تحول "صاحب المنزل" للانعكاسات ، فإننا ننفذ أولاً العمليات اللازمة لذلك.

تعد عملية إضافة / طرح وضرب عددية بسيطة. يبدو ضخمًا إلى حد ما ، لكن لا يوجد شيء معقد هنا ، لأن الحساب بسيط.


ولكن للتفكير ، نحن بحاجة إلى تشغيل ضرب المصفوفة في حالة معينة. ضرب متجه البعد 4 × 4 × 1 × 4 (تم نقله) إذا كنت معتادًا على مصفوفة الرياضيات ، فأنت تعلم أنه مع هذا الضرب ، ستحتاج إلى النظر إلى الأعداد القصوى للبعد ، وستحصل على البعد من المصفوفة في المخرجات ، أي في هذه الحالة 4x4. هناك معلومات كافية حول كيفية مضاعفة المصفوفات ، لذلك لن نرسم هذا. فيما يلي مثال لحالة معينة ستكون مفيدة في المستقبل.

تحول صاحب المنزل

بحثًا عن كيفية عكس كائن نسبة إلى أي محور ، غالبًا ما صادفت نصيحة لوضع مقياس سلبي في الاتجاه الضروري. هذه نصيحة سيئة للغاية في سياق الوحدة ، لأنها تكسر الكثير من الأنظمة في المحرك (الذبح ، الاصطدام ، إلخ.) في بعض الخوارزميات ، يتحول هذا إلى حسابات غير تافهة تمامًا إذا كنت بحاجة إلى التفكير بشكل تافه فيما يتعلق بـ Vector3.up أو Vector3.forward ، ولكن في اتجاه تعسفي. لم يتم تنفيذ طريقة الانعكاس في وحدة خارج الصندوق نفسه ، لذلك قمت بتطبيق طريقة Householder .

لا يستخدم تحويل Householder في رسومات الكمبيوتر فحسب ، بل في هذا السياق هو تحول خطي يعكس كائنًا متعلقًا بمستوى يمر عبر "الأصل" ويتم تحديده بواسطة المستوى العادي إلى المستوى. في العديد من المصادر ، يتم وصفه بطريقة معقدة وغير مفهومة ، على الرغم من أن صيغته أولية.

H = I-2 * n * (n ^ T)

حيث H هي مصفوفة التحويل ، في حالتنا هي Matrix4x4.identity ، و n = Vector4 جديدة (planeNormal.x ، planeNormal.y ، planeNormal.z ، 0). يعني الرمز T تبديل ، أي بعد ضرب n * (n ^ T) نحصل على مصفوفة 4 × 4.

ستكون الأساليب المستخدمة سهلة الاستخدام وسيكون التسجيل مضغوطًا للغاية.


هام: المستوى الطبيعي يجب أن يكون طبيعيًا (وهو منطقي) ، والإحداثي الأخير n يجب أن يكون 0 ، بحيث لا يكون هناك أي تأثير للامتداد في الاتجاه ، لأنه يعتمد على طول المتجه n.

الآن للراحة في الوحدة نحن نطبق طريقة التمديد للتحول


هذا كل شيء لهذا اليوم ، إذا كانت هذه السلسلة من المقالات ستظل مثيرة للاهتمام ، فسأكشف أيضًا عن تطبيقات الرياضيات الأخرى في تطوير اللعبة. هذه المرة لن يكون هناك أي مشروع ، حيث يتم وضع جميع الكود في المقال ، ولكن المشروع مع تطبيق معين سيكون في المقال التالي. من الصورة يمكنك تخمين ماذا ستكون المقالة القادمة.



شكرا لاهتمامكم!