بحاجة الى مزيد من طمس مختلفة

صورة ضبابية مع مرشح Gaussian Blur يستخدم على نطاق واسع في مجموعة واسعة من المهام. لكن في بعض الأحيان تريد تنوعًا أكبر بقليل من مرشح واحد فقط لجميع المناسبات ، حيث يمكن لمعلمة واحدة فقط أن تضبط نفسها - حجمها. في هذه المقالة ، سوف نلقي نظرة على العديد من التطبيقات الضبابية الأخرى.

مقدمة

إن تأثير Gaussian Blur هو عملية خطية ويمثل رياضياً ملفاً للصورة مع مصفوفة المرشح. في هذه الحالة ، يتم استبدال كل بكسل في الصورة بمجموع وحدات البكسل القريبة التي تم التقاطها بعوامل ترجيح معينة.

يُطلق على المرشح اسم Gaussian لأنه مبني على وظيفة تُعرف باسم Gaussian ، $$$e ^ {- x ^ 2}$ :



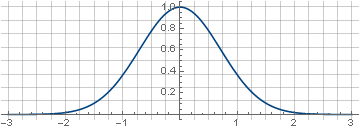
يتم الحصول على نسخة ثنائية الأبعاد من خلال دورانها حول المحور الإحداثي ، $$$e ^ {- (x ^ 2 + y ^ 2)}$ :



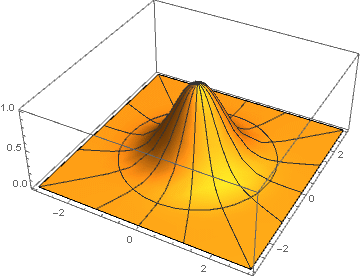
هنا لكل زوج من الإحداثيات $$$(س ، ذ)$ يتم حساب المسافة إلى المركز من خلال الصيغة $$$\ sqrt {x ^ 2 + y ^ 2}$ ، والتي يتم تمريرها كوسيطة للدالة الغوسية - وكما ترون بسهولة ، $$$e ^ {- \ left (\ sqrt {x ^ 2 + y ^ 2} \ right) ^ 2}$ خفضت إلى $$$e ^ {- (x ^ 2 + y ^ 2)}$ .

مصفوفة مبنية على قطعة $$$[- 3.3]$ ومع وجود مستوى معين من أخذ العينات ، سيبدو كما يلي:

$$

$$\ left (\ start {array} {ccccccc} 1.52 \ times 10 ^ {- 8} & 2.26 \ times 10 ^ {- 6} & 0.0000454 & 0.000123 & 0.0000454 & 2.26 \ times 10 ^ {- 6} & 1.52 \ الأوقات 10 ^ {- 8} \\ 2.26 \ times 10 ^ {- 6} & 0.000335 & 0.00674 & 0.01834 & 0.00674 & 0.000335 & 2.26 \ times 10 ^ {- 6} \\ 0.0000454 & 0.00674 & 0.135 & 0.368 & 0.135 & 0.00674 & 0.0000454 \\ 0.000123 & 0.0183 & 0.368 & 1.00 & 0.368 & 0.0183 & 0.000123 \\ 0.0000454 & 0.00674 & 0.135 & 0.368 & 0.135 & 0.00674 & 0.0000454 \\ 2.26 \ times 10 ^ {- 6} & 0.000335 & 0.00674 & 0.0183 & 0.00674 & 0.000335 & 2.26 \ times 10 ^ {- 6} \\ 1.52 \ times 10 ^ {- 8} & 2.26 \ times 10 ^ {- 6} & 0.0000454 & 0.000123 & 0.0000454 & 2.26 \ times 10 ^ { -6} & 1.52 \ times 10 ^ {- 8} \\ \ end {array} \ right)$$

أو ، إذا نظرنا إلى قيم عناصر المصفوفة على أنها مستوى سطوع ، مثل هذا:



فيما يتعلق بمعالجة الإشارات ، يُطلق على ذلك الاستجابة النبضية ، لأن هذا هو بالضبط ما ستظهره نتيجة الالتواء لهذا الفلتر مع دفعة واحدة (في هذه الحالة ، بكسل).

في البداية ، يتم تعريف Gaussian على فاصل لانهائي. ولكن نظرًا لحقيقة أنه يتحلل بسرعة كبيرة ، فمن الممكن أن يستبعد من الحسابات القيم القريبة من الصفر - لأنها لا تزال لن تؤثر على النتيجة. في التطبيقات الحقيقية ، يعد تطبيع القيمة ضروريًا أيضًا حتى لا يتغير سطوع الصورة بعد الالتفاف ؛ وفي حالة عدم وضوح الصورة التي يكون لكل بكسل فيها نفس اللون ، يجب ألا تتغير الصورة نفسها.

للراحة ، غالبًا ما يستخدم التطبيع في الإحداثيات ، من خلال إدخال معلمة إضافية $$$\ سيجما$ (اقرأ باسم "سيغما") - للنظر في حجة في النطاق $$$[- 1،1]$ و $$$\ سيجما$ يحدد نسبة ضغط غاوسي:

$$

$$\ frac {e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

تطبيع المفرق $$$2 \ pi \ sigma ^ 2$ تم الحصول عليها هنا بشكل تحليلي من خلال جزء لا يتجزأ محدد في اللانهاية:

$$

$$\ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \، dx dy = 2 \ pi \ sigma ^ 2$$

بسبب حقيقة أن المساواة تحمل $$$e ^ {- \ left (x ^ 2 + y ^ 2 \ right)} = e ^ {- x ^ 2} e ^ {- y ^ 2}$ يمكن تنفيذ عدم وضوح Gaussian بالتتابع ، أولاً في الصفوف ثم في الأعمدة - مما يتيح لك توفير الكثير من العمليات الحسابية. في هذه الحالة ، من الضروري استخدام صيغة التطبيع للحالة أحادية البعد -

$$

$$\ frac {e ^ {- \ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

ابدأ

بالنسبة للمرشح التعسفي ، نحتاج أولاً إلى تحديد وظيفة التوهين الخاصة بنا من متغير واحد $$$و$ ، حيث يتم الحصول على وظيفة اثنين من المتغيرات بالتناوب عن طريق استبدال $$$x$ على $$$\ sqrt {x ^ 2 + y ^ 2}$ اين $$$x$ و $$$ذ$ هذه هي إحداثيات عنصر المصفوفة في النطاق $$$(- 1،1) دولا$ ، والذي يستخدم بعد ذلك لملء عناصر المصفوفة. لن يتم النظر في التطبيع بشكل تحليلي ، ولكن يكون ملخصًا مباشرًا لجميع عناصر المصفوفة - هذا أبسط وأكثر دقة - لأنه بعد التقدير ، تصبح الوظيفة "ضعيفة" وستتوقف قيمة التطبيع على مستوى التقدير.

في حالة ترقيم عناصر المصفوفة من البداية ، فإن الإحداثيات $$$x$ او $$$ذ$ يتم حسابها بواسطة الصيغة

$$

$$\ frac {2 index} {size-1} -1$$

اين $$ - الرقم التسلسلي للعنصر في الصف أو العمود ، و $$ - العدد الإجمالي للعناصر.

على سبيل المثال ، في المصفوفة 5 في 5 ، سيبدو كما يلي:

$$

$$\ left (\ start {array} {ccccc} f (-1، -1) & f \ left (- \ frac {1} {2}، - 1 \ right) & f (0، -1) & f \ left (\ frac {1} {2}، - 1 \ right) & f (1، -1) \\ f \ left (-1، - \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2} ، - \ frac {1} {2} \ right) & f \ left (0 ، - \ frac {1} {2} \ right) & f \ left (\ frac { 1} {2} ، - \ frac {1} {2} \ right) & f \ left (1 ، - \ frac {1} {2} \ right) \\ f (-1.0) & f \ left (- \ frac {1} {2} ، 0 \ right) & f (0،0) & f \ left (\ frac {1} {2} ، 0 \ right) & f (1،0) \\ f \ left (-1 ، \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2} ، \ frac {1} {2} \ right) & f \ left (0 ، \ frac {1} {2} \ right) & f \ left (\ frac {1} {2} ، \ frac {1} {2} \ right) & f \ left (1 ، \ frac {1} {2 } \ right) \\ f (-1،1) & f \ left (- \ frac {1} {2} ، 1 \ right) & f (0،1) & f \ left (\ frac {1} { 2} ، 1 \ right) & f (1،1) \\ \ end {array} \ right)$$

أو إذا استبعدنا القيم الحدية التي لا تزال صفرية ، فسيتم حساب الإحداثيات بواسطة الصيغة

$$

$$\ frac {2 index-size + 1} {size}$$

وسوف تتخذ المصفوفة تبعا لذلك

$$

$$\ left (\ start {array} {ccccc} f \ left (- \ frac {4} {5} ، - \ frac {4} {5} \ right) & f \ left (- \ frac {2} { 5} ، - \ frac {4} {5} \ right) & f \ left (0 ، - \ frac {4} {5} \ right) & f \ left (\ frac {2} {5} ، - \ frac {4} {5} \ right) & f \ left (\ frac {4} {5} ، - \ frac {4} {5} \ right) \\ f \ left (- \ frac {4} {5 }، - \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}، - \ frac {2} {5} \ right) & f \ left (0، - \ frac {2} {5} \ right) & f \ left (\ frac {2} {5} ، - \ frac {2} {5} \ right) & f \ left (\ frac {4} {5} ، - \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5} ، 0 \ right) & f \ left (- \ frac {2} {5} ، 0 \ right ) & f (0،0) & f \ left (\ frac {2} {5} ، 0 \ right) & f \ left (\ frac {4} {5} ، 0 \ right) \\ f \ left ( - \ frac {4} {5} ، \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5} ، \ frac {2} {5} \ right) & f \ left (0 ، \ frac {2} {5} \ right) & f \ left (\ frac {2} {5} ، \ frac {2} {5} \ right) & f \ left (\ frac {4} {5} ، \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5} ، \ frac {4} {5} \ right) & f \ left (- \ frac {2} {5} ، \ frac {4} {5} \ right) & f \ left (0 ، \ frac {4} {5} \ right) & f \ left (\ frac {2} {5} ، \ frac {4} {5} \ right) & f \ left (\ frac {4} {5} ، \ frac {4} {5} \ right) \\ \ end {array} \ right)$$

بعد أن يتم حساب عناصر المصفوفة بواسطة الصيغة ، من الضروري حساب مجموعها وتقسيم المصفوفة إليها. على سبيل المثال ، إذا حصلنا على مصفوفة

$$

$$\ left (\ start {array} {ccc} 1 & 4 & 1 \\ 4 & 20 & 4 \\ 1 & 4 & 1 \\ \ end {array} \ right)$$

عندها سيكون مجموع كل عناصرها 40 ، وبعد التطبيع سوف يأخذ الشكل

$$

$$\ left (\ start {array} {ccc} \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ frac {1} {10} & \ frac {1} {2} & \ frac {1} {10} \\ \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ end {array } \ اليمين)$$

ويصبح مجموع كل عناصره 1.

التوهين الخطي

أولاً ، خذ أبسط وظيفة - الخط:

$$

$$\ left \ {\ start {array} {ll} 1-x ، & x <1 \\ 0 ، & x \ geqslant 1 \\ \ end {array} \ right.$$

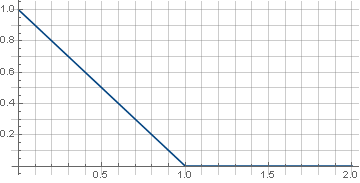
يتطلب التعريف المستمر للقطاعات هنا أن الوظيفة مضمونة للانتقال إلى الصفر وعدم ظهور أي قطع أثرية في زوايا المصفوفة أثناء الدوران. بالإضافة إلى ذلك ، بما أن التدوير يستخدم جذر مجموع مربعات الإحداثيات ، وهو أمر إيجابي دائمًا ، يكفي تحديد الوظيفة فقط في الجزء الموجب من القيم. نتيجة لذلك ، نحصل على:

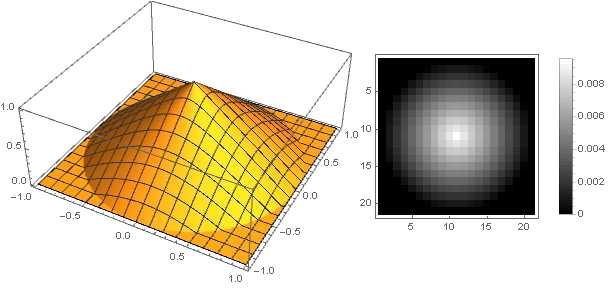
التوهين الخطي الناعم

يمكن أن يؤدي الانتقال الحاد من الخط المائل إلى الوظائف الصفرية إلى تناقض مع الإحساس بالجمال. لحلها ، سوف تساعدنا الوظيفة.

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

فيها $$$ن$ يحدد "صلابة" الالتحام ، $$$n> 1 دولا$ . على سبيل المثال $$$ن = 3 دولارا$ نحن نحصل عليها

$$

$$\ left \ {\ start {array} {ll} 1- \ frac {3 xx ^ 3} {2} ، & x <1 \\ 0 ، & x \ geqslant 1 \\ \ end {array} \ right.$$

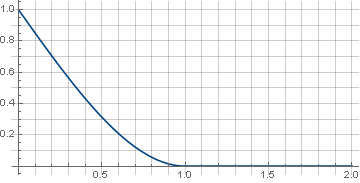
والمرشح نفسه سيبدو

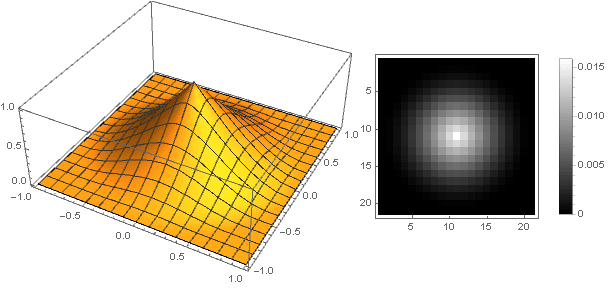
التخفيف الزائدي

يمكن جعل المرشح "أكثر حدة" وأكثر سلاسة إلى الصفر عن طريق القيام بوظيفة أخرى ، على سبيل المثال ، القطع الزائد ، وضمان الانتقال السلس إلى الصفر عن طريق الجمع مع القطع المكافئ.



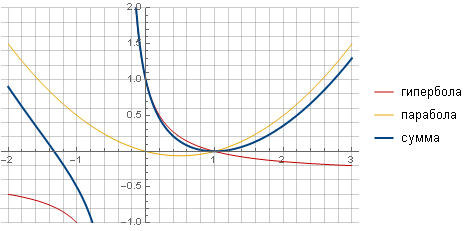
بعد كل العمليات الحسابية والتبسيط ، نحصل على الصيغة

$$

$$\ left \ {\ start {array} {ll} \ frac {(x-1) ^ 2 (k x + k + 1)} {(k + 1) (k x + 1)} ، & x <1 \\ 0 و & x \ geqslant 1 \\ \ end {array} \ right.$$

في أي معلمة $$$ك> 0 دولا$ يحدد طبيعة التوهين:



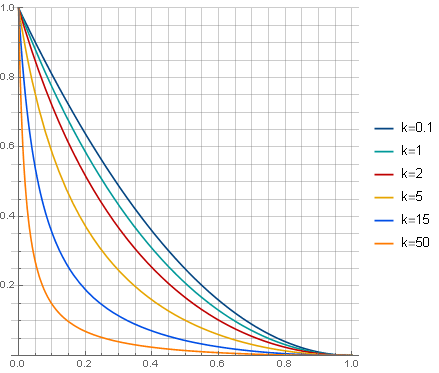
والمرشح نفسه سوف ننظر (ل $$$ك = 5 دولا$ ) كيف

خوخه تأثير

يمكنك الذهاب بطريقة أخرى - لجعل الجزء العلوي من المرشح غير حاد ، ولكن غبي. أسهل طريقة لتنفيذ ذلك هي تعيين وظيفة التخميد كدالة ثابتة:

$$

$$\ left \ {\ start {array} {ll} 1 ، & x <1 \\ 0 ، & x \ geqslant 1 \\ \ end {array} \ right.$$

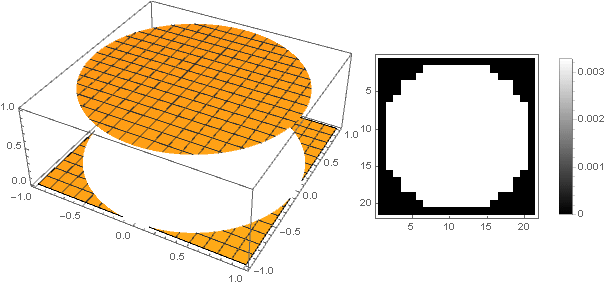
لكن في هذه الحالة ، نحصل على بكسل قوي ، يتناقض مع الإحساس بالجمال. لجعلها أكثر سلاسة عند الحواف ، سوف تساعدنا المكافئ ذي الترتيب العالي ، والذي من خلال تحريكه على طول المحور الإحداثي وتربيعه ، نحصل عليه

$$

$$\ left \ {\ start {array} {ll} \ left (1-x ^ n \ right) ^ 2 ، & x <1 \\ 0 ، & x \ geqslant 1 \\ \ end {array} \ right.$$

متغير المعلمة $$$ن$ يمكنك الحصول على مجموعة واسعة من خيارات التصفية:

$$

$$ن = 0.5 دولا$$

$$

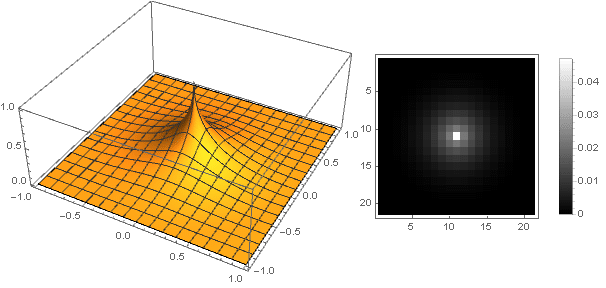
$$ن = 2 دولا$$

$$

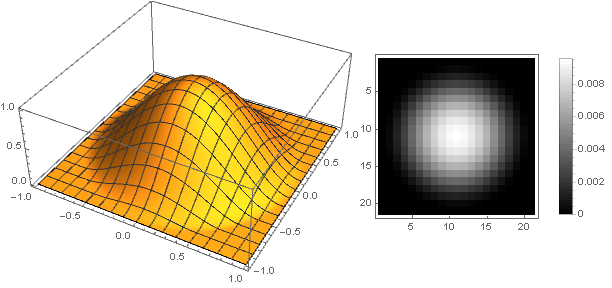
$$ن = 10 دولا$$

$$

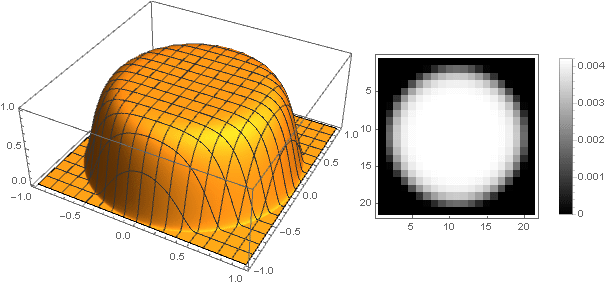
$$ن = 50 دولا$$

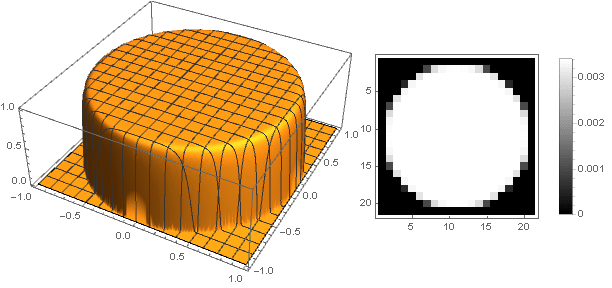
ومن خلال تعديل وظيفة التخميد قليلاً ، يمكنك جعل الحلقة عند حواف المرشح أكثر وضوحًا ، على سبيل المثال مثل هذا:

$$

$$\ left \ {\ start {array} {ll} \ left (1-x ^ n \ right) ^ 2 \ left (d + x ^ m \ right) ، & x <1 \\ 0 ، & x \ geqslant 1 \\ \ end {array} \ right.$$

هنا المعلمة $$$د$ يحدد ارتفاع المركز ، و $$$م دولا$ - حدة الانتقال إلى الحواف.
ل $$$d = 0.2 ، m = 2 ، n = 10$ نحن نحصل عليها



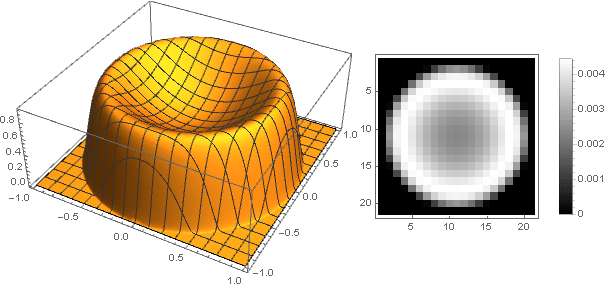
لكن ل $$$d = 0 ، m = 12 ، n = 2$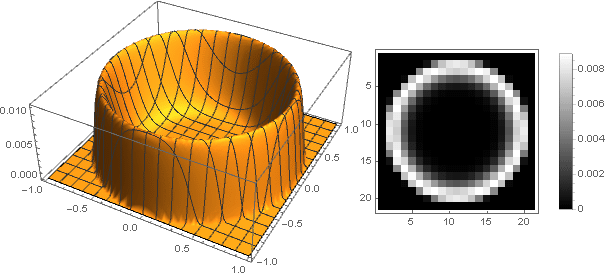

الاختلافات غاوس

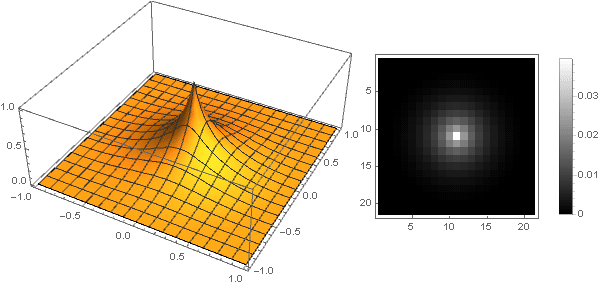
يمكن أيضًا تعديل وظيفة Gaussian نفسها مباشرةً. الطريقة الأكثر وضوحًا للقيام بذلك هي تحديد المعلِّم - لن نفكر في الأمر الآن ، ولكن نأخذ خيارًا أكثر إثارة للاهتمام:

$$

$$\ left \ {\ start {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}} ، & -1 <x <1 \\ 0 ، وإلا \\ \ end { مجموعة} \ اليمين.$$

بسبب حقيقة أنه مع $$$x$ قاسم الوحدة $$$x ^ 2-1$ يميل إلى الصفر الكسر $$$\ frac {k x ^ 2} {x ^ 2-1}$ يميل إلى ناقص اللانهاية ، ويميل الأس نفسه إلى الصفر. وبالتالي تقسيم بواسطة $$$x ^ 2-1$ يسمح بضغط مجال تعريف الوظيفة مع $$$(- \ infty ، \ infty)$ قبل $$$(- 1،1) دولا$ . علاوة على ذلك ، متى $$$س = \ مساء 1 دولا$ بسبب القسمة على صفر ( $$$1 ^ 2-1 = 0$ ) قيمة الوظيفة غير محددة ، لكن لها حدين - الحد من جهة (من الداخل) هو صفر ، ومن ناحية أخرى ، اللانهاية:

$$

$$\ underset {x \ to 1 ^ -} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ to 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

نظرًا لعدم تضمين قيم الحدود في الفاصل الزمني ، فإن الصفر في الحد على جانب واحد يكفي فقط. ومن المثير للاهتمام ، أن هذه الخاصية تمتد إلى جميع مشتقات هذه الوظيفة ، والتي تضمن مطابقة مثالية مع صفر.

المعلمة $$$ك$ يحدد التشابه مع الغاوسي - كلما كان أكبر ، كان التشابه أقوى - بسبب حقيقة وجود قسم خطي متزايد $$$\ frac {1} {x ^ 2-1}$ تقع في وسط الوظيفة. يمكن للمرء أن يفترض أنه بسبب هذا ، في الحد ، يمكنك الحصول على Gaussian الأصلي - ولكن للأسف ، لا - لا تزال الوظائف مختلفة.



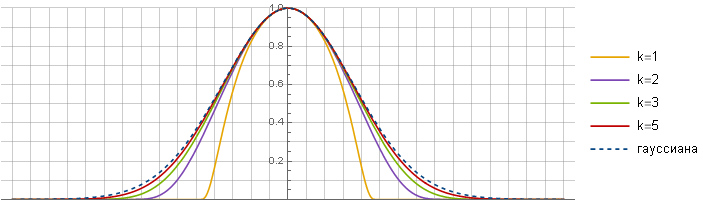
الآن يمكنك أن ترى ما حدث:

$$

$$ك = 5 دولا$$

$$

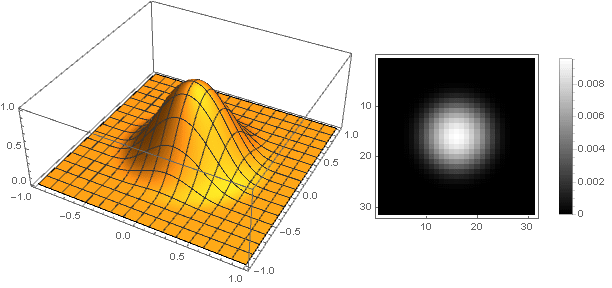
$$ك = 2 دولا$$

$$

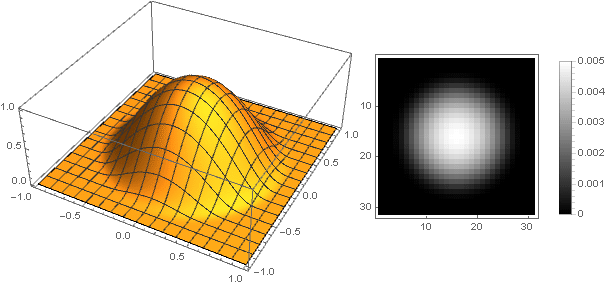
$$ك = 0.5 دولا$$

$$

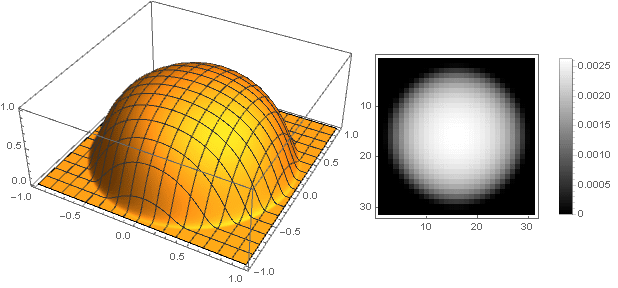
$$ك = 0.1 دولا$$

$$

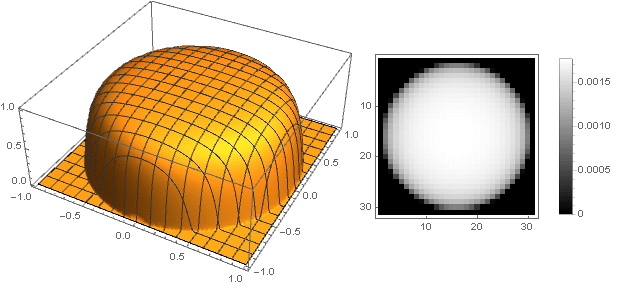
$$ك = 0.01 دولا$$

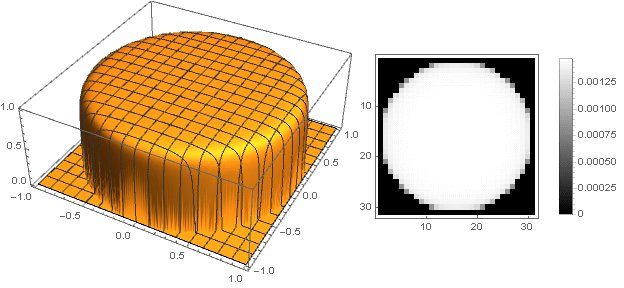
اختلافات الشكل

عن طريق تغيير وظيفة الانتقال من إحداثيين إلى واحد $$$\ sqrt {x ^ 2 + y ^ 2}$ ، يمكنك الحصول على أشكال أخرى ، وليس مجرد قرص. على سبيل المثال:

$$

$$f \ left (\ frac {\ left | x-y \ right | + \ left | x + y \ right |} {2} \ right)$$

$$

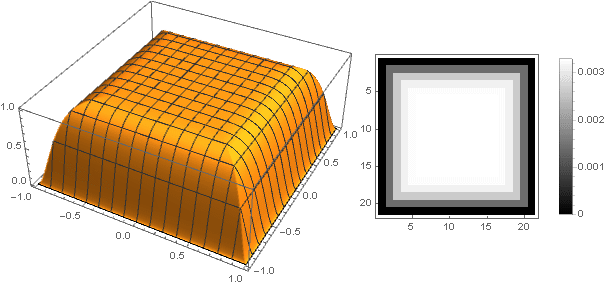
$$f (\ left | x \ right | + \ left | y \ right |)$$

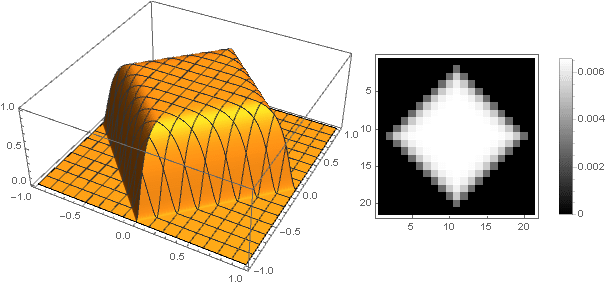
من خلال الانتقال إلى أرقام معقدة ، يمكنك إنشاء أشكال أكثر تعقيدًا:

$$

$$f \ left (\ frac {\ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {0} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac { 2} {3}} \ right) \ right |} {\ sqrt {3}} \ right)$$

$$

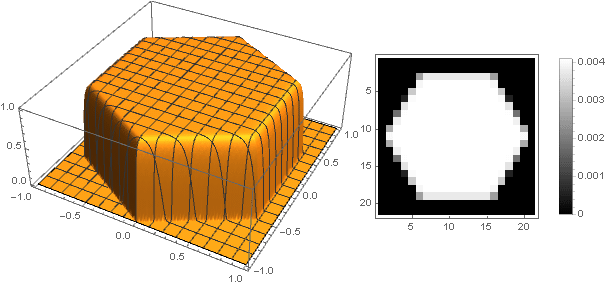
$$f \ biggl (10 \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {8}} \ right) \ right | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

$$

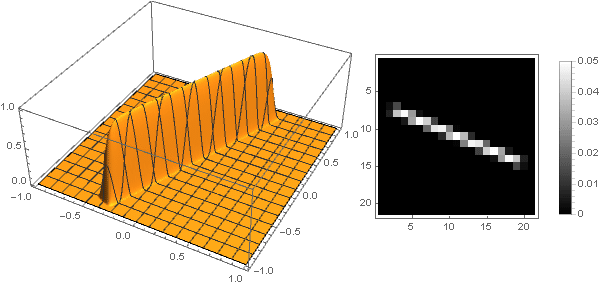
$$f \ biggl (\ biggl | 5 \ left | x + iy \ right | (x + iy) \ Re \ biggl (\ cos \ left (\ frac {5} {2} \ arg (x + iy) \ right ) \ biggr) \ biggr | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

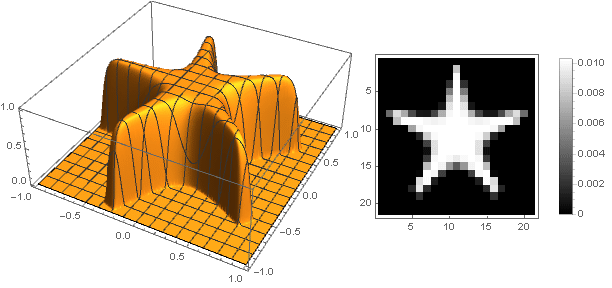
في هذه الحالة ، يجب عليك التأكد من أنه عند تحويل الإحداثيات لا تتجاوز الفاصل الزمني $$$(0،1)$ - حسنًا ، أو العكس ، أعيد تعريف وظيفة التخميد للقيم السلبية للوسيطة.

بعض الأمثلة المحددة

مقال لن يكون كاملا دون اختبار عملي على صور محددة. نظرًا لعدم وجود عمل علمي لدينا ، فلن نأخذ صورة لينا أيضًا - سنأخذ شيئًا ناعمًا ورقيقًا:


















نفس المرشحات ، ولكن للنص:

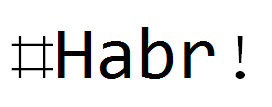
الخاتمة

وبالمثل ، يمكنك إنشاء عوامل تصفية أكثر تعقيدًا ، بما في ذلك عوامل التوضيح أو الخطوط العريضة ؛ وأيضا تعديل تلك النظر بالفعل.

من الأمور ذات الأهمية الخاصة التصفية غير الخطية ، عندما تعتمد قيم معاملات المرشح على الإحداثيات أو الصورة التي يتم ترشيحها مباشرة - ولكن هذا موضوع يخضع بالفعل للدراسات الأخرى.

يعتبر إخراج وظائف الالتحام مع الثابت بمزيد من التفصيل هنا . يمكن أيضًا استخدام وظائف النافذة الموضحة هنا كدالة تخفيف - كل ما هو مطلوب هو توسيع الوسيطة c (0،1) إلى ( $$$\ frac {1} {2}$ ، 1) أو في البداية النظر في وظائف النافذة من خلال الصيغة $$$\ frac {1} {2} \ left (f \ left (\ frac {t x + 1} {t-1} \ right) - f \ left (\ frac {t x-1} {t-1} \ اليمين) \ اليمين)$ .

يمكن تنزيل المستند المصدر Wolfram Mathematica لهذه المقالة هنا .