بدلا من المقدمة
لنفترض أنك جالست على كرسي دافئ في المساء ، حدث لك فكرة مجنونة: "حسنًا ، لماذا لا أعرف لماذا يتم اختيار عوامل القياس النموذجية بشكل عشوائي ولماذا يعمل كل شيء؟"
هذا منحدر زلق - تعتقد أن بضع أمسيات مع قراءة مهل لفصل "التعلم العميق" أو مقاطع يوتيوب لمدة 5 دقائق من مختلف MOOCs كافية ؛ في الواقع ، لإيجاد الفهم ، وليس الوهم ، يتطلب الأمر وقتًا لا بأس به (حسنًا ، بالتأكيد ليس أقل من ستة أشهر لأكثر المتعصبين) ؛ ولكن الشيء الأكثر حزناً هو أن الربح من هذا الحدث ليس واضحًا - لحسن الحظ (أو للأسف) ، العالم غير مرتب وفقًا لقوانين الرياضيات ، وإذا كنت طبيبة فيزياء ثلاث مرات ، فلن تعمل بعض الطرز بشكل أفضل إلا إذا قمت بالرمي لديهم المزيد من البيانات التي سبق معالجتها أو بناء مجموعة ضخمة.
أنا أعتبر أنه من واجبي أن أحذرك من أن هذا طريق منحنى ، وأنه من الممكن ألا تؤتي الاستثمارات في الرياضيات ثمارها بمجرد رغبتك. لكن الرياضيات مثيرة للاهتمام في حد ذاتها ، مهما كانت التطبيقات. علاوة على ذلك ، إذا كنت مهتمًا ، وما يحدث في هذا الصندوق الأسود بمعلمات تشعبية ، فهذا يعني أن الرياضيات غالبًا ما تكون غير مبالية بك.
شيء آخر حول توصياتي: أنا لا أحب الأدب الرياضي ، الذي يعج بالمؤشرات واللآلئ مثل "a'ijk مع ثلاثة شُرَط تحتية وقبعة مترافقة". أعتقد أن الأفكار أكثر أهمية من الاستنتاجات الصارمة. في الوقت نفسه ، يجب ألا تنزلق الأفكار إلى "الأيدي" ؛ كل شيء يجب أن يكون صارمًا تمامًا. لا أحب الكتب مثل بورباكي وكنوت. في رأيي ، هذه الكتب مخصصة لأي شيء ، ولكن ليس للقراءة وليس لدراسة الموضوع. أنها جيدة مثل الروابط والموسوعات.
في النهاية ، سأستشهد بشيء من برتراند راسل:
إقليدس يحتقر الأداة العملية التي قدمها أفلاطون. يقولون أن طالبًا واحدًا ، بعد الاستماع إلى الأدلة ، سأل عما فاز به من خلال دراسة الهندسة ؛ ثم دعا إقليدس عبدًا وقال: "أعط الشاب فلسًا ، لأنه يجب أن يستفيد بالتأكيد مما يدرسه".
الآن سأنتقل إلى الجزء الرئيسي.
المتطلبات الأساسية
- أفترض أنك أكثر أو أقل توجهاً في دورة مدرسية في الرياضيات.
- أفترض أنك لست باللغة الإنجليزية بشكل كامل مع "أنت" ، لأن الكثير من الأدب والدورات الجيدة تكتب وتروى بهذه اللغة. اللغة الإنجليزية الرياضية ليست مخيفة مثل اللغة الإنجليزية بشكل عام ؛ هذا هو مفردات محدودة نوعا ما مع جمل مبنية بشكل قياسي ، من دون mashmash من الوقت ، دون شغب من الألوان ، الخ
- أفترض أن لديك حبلًا يمكنك ربط كرسيك به.
مستويات الصعوبة
ليس سراً أن الكثير من الأدب كتب على كل تخصص رياضي ، وأحيانًا يصبح الاختيار البسيط للكتاب الصحيح مشكلة. سأسلط الضوء على عدة مستويات من التعقيد في الأدبيات التي تعرفها إلى أين تتدخل وأين تتسلق (حتى الآن) لم يكن ضروريًا (أو ما يمكنك الرجوع إليه للحصول على مزيد من المعلومات الكاملة).
- إحضاره - العمود الفقري الرئيسي ؛ هذه هي الكتب التي تسمى "يجب أن يكون".
- يؤذيني كثيرًا - مستوى أعلى ، يتيح لك إلقاء نظرة على المستوى 1 من وجهة نظر عين الطير ، وينظم المعرفة ، ويجمع بين مجالات المعرفة المختلفة.
- كابوس - للقوي في الروح ، ومستوى مهمات ، لعشاق الرياضيات وأبراج العاج.
خارطة الطريق
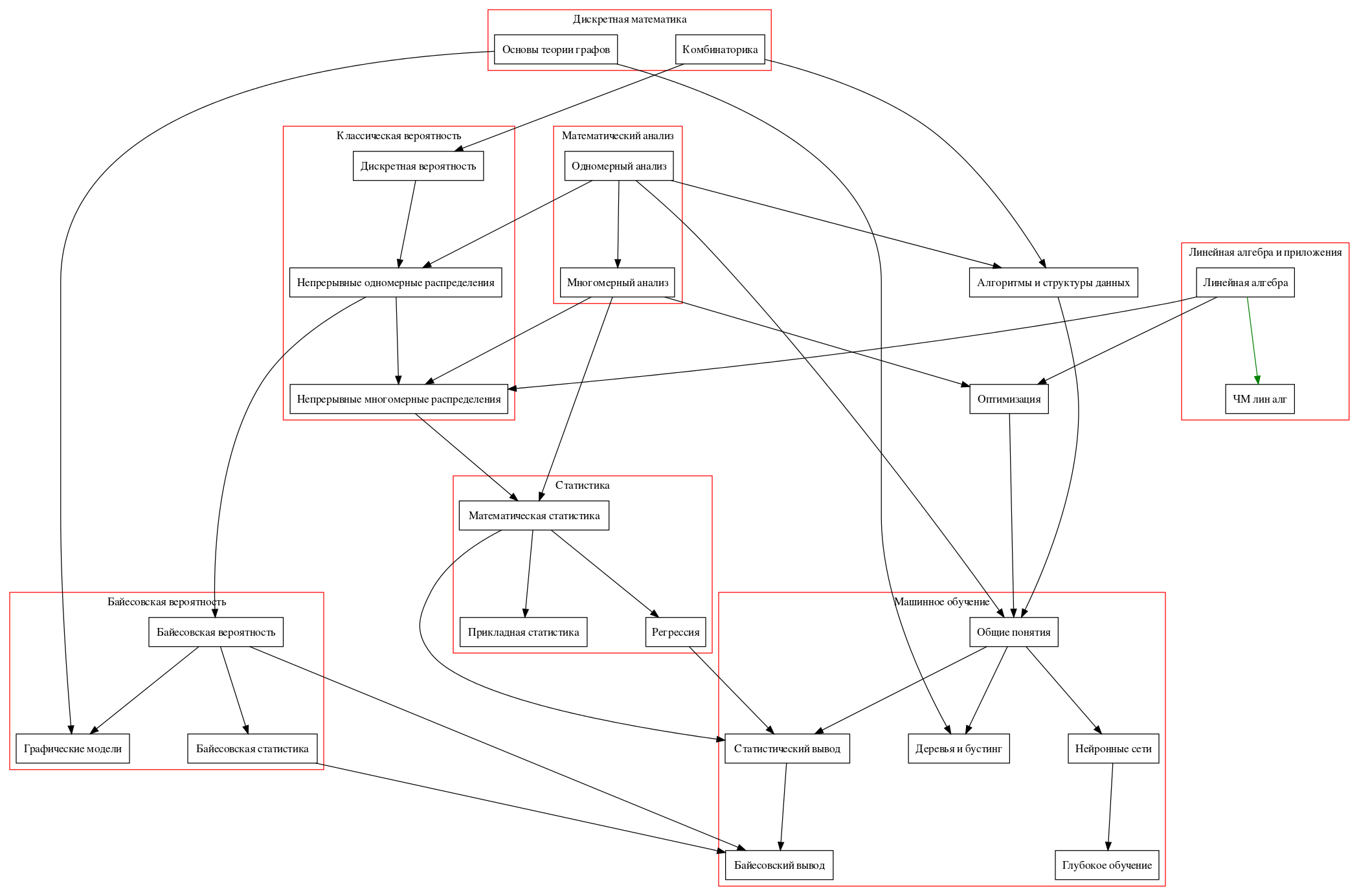
سأنتقل في الواقع إلى دورات محددة.
التحليل ، هو حساب التفاضل والتكامل
يدرس بشكل مثير للاهتمام في الجامعات الروسية: معظمهم ، بعد عدة سنوات من نهاية الدورة ، يتذكر بشكل غامض فقط بعض التكاملات هناك ، ويبدو أن هناك شيء آخر. وهذا على الرغم من حقيقة أن التحليل هو تخصص ، في الواقع ، هو واحد من الأساسيات في الرياضيات بشكل عام. كقاعدة عامة ، لا توجد جسور من النظرية إلى الممارسة ، وهذه الدورة ، مثل الجزيرة الطائرة ، تحوم في مكان ما في الرأس ، وهي منفصلة تمامًا عن الحياة الحقيقية. من الضروري التغلب على هذا عن طريق حل المشاكل ، علاوة على ذلك ، ليس فقط من مجال الرياضيات ، ولكن أيضًا شيء من "الحياة الحقيقية" أمر مرغوب فيه.
ما تحتاج إلى معرفته من التحليل؟
الأشياء الرئيسية التي سنحتاج إليها هي مفاهيم الحد ، الاستمرارية ، الاشتقاق ، دالة العديد من المتغيرات ، التدرج ، التكامل ، التكامل مع الحد الأعلى المتغير ، التكامل متعدد الأبعاد *.
الأدب
إحضاره : كل شيء قياسي أكثر أو أقل هنا -
Piskunov / Fichtenholtz .
يؤذيني كثيرا :
Zorich ، المجلد 1 . انا احب هذا الكتاب كثيرا جدا هذا ليس كتابًا مدرسيًا ، ولكنه رواية في الصيغ ، مثل يوجين أونجين. لسوء الحظ ، يعد الأمر أكثر تعقيدًا من دورات التحليل القياسية نظرًا لحقيقة أنه يتم تقديم العديد من الأشياء فيه بشكل عام ، وتحتاج إلى التعود عليها ؛ ولكن بسبب هذا القاسم المشترك ، ترتبط العديد من الأشياء المتباينة ببعضها البعض (انظر نفس الحدود على القاعدة).
كابوس :
Zorich المجلد 1 + المجلد 2 ، رودين "أساسيات التحليل الرياضي" ، لفيف "محاضرات حول التحليل الرياضي" ، رامانان "حساب التفاضل والتكامل العالمي".بشكل عام ، الملخص هنا هو: أدب التحليل ، حتى باللغة الروسية ، ممتلئ ؛ الكتب المدرسية تميل إلى أن تكون رياضية بحتة. كإضافة إلى الكتب المدرسية من المستوى 2-3 ، يمكنني تقديم المشورة للعديد من الدورات التدريبية:
لم ألق نظرة على الدورات التدريبية من قاعة المحاضرات في MIPT حول التحليل ، ولكن من أجل اكتمالها ، سأقدم أيضًا:
الممارسة
إن ممارسة وتطبيق المعرفة المكتسبة ليس "اختياريًا" فحسب ، بل إلزامي تمامًا ، وإلا فإن النظرية بأكملها ستعلق عليك بثقل ميت ، وستغرق بسرعة إلى أسفل دون أن تدرك ذلك.
أقترح دراسة الخيارات التالية:
Demidovich ، مجموعات المشكلات من دورات MIT (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
الجبر الخطي
الخبز اليومي لعلوم البيانات والعلوم بشكل عام. لسوء الحظ ، تعلم الناس أن يحلوا المعادلات الخطية وأنظمتها بشكل جيد ؛ بالنسبة لمعادلات الدرجة 2 وما فوق ، هناك كل أنواع النظريات غير المبالية (الجبر التبادلي ، الهندسة الجبرية ، وغيرها). لذلك ، في تحليل البيانات ، تُستخدم النماذج الخطية أساسًا (أو النماذج الخطية المعممة ، مثل الانحدار اللوجستي ، الإدراك الحسي ، إلخ).
هناك العديد من الكتب حول الجبر الخطي باللغة الروسية. المشكلة هي أنها مكتوبة إما لعلماء الرياضيات ، أو أن هناك العديد من الفهارس المكتئب عليها (وليس هناك غابة مرئية وراء الأشجار). في الغالب يكون التركيز في الدورات الجامعية على نموذج الأردن ؛ غالبًا ما لا يتم ذكر النماذج القياسية الأخرى ؛ هناك غاوس وكرامر غبي ، ولكن نادرا ما يحدث حول LU ، حول SVD.
ما تحتاج إلى معرفته من الجبر الخطي؟
مفهوم ناقل وناقل الفضاء؛ مفهوم المشغل الخطي ؛ اتصالات المشغلين والمصفوفات ؛ تحلل المصفوفة (LU ، SVD على الأقل) ؛ eigenvectors والقيم الذاتية؛ متعامد ، مشغلي وحدوي ؛ مشغلي المتماثل و hermitian. الأشكال التربيعية ، الاختزال في المحاور الرئيسية.
الأدب
إحضاره :
دورة OCW-MIT الخاصة بـ Gilbert Strang حول الجبر الخطي + كتابه .
ocw.mit.edu/courses/mathematics/18-06- Lineear-algebra-spring-2010/index.htmأفضل شيء في هذه الدورة هو عدم وجود نظريات "معقدة" وأحمق من الجبر الخطي ، وجميع أنواع المساحات المزدوجة ، وعدد كبير من المشاكل في الكتاب ، ونهج موجه نحو الممارسة (وليس "ما هو عليه" ، ولكن "كيفية حسابه"). المزيد من الدورات التوضيحية في الجبر الخطي لم أقابلها بعد.
يؤذيني الكثير :
أكسلر "الجبر الخطي عمله الحق" ؛ جلفاند "محاضرات حول الجبر الخطي " ؛ MIPT course
lectoriy.mipt.ru/course/LinearAlgebra ؛
Kostrikin "مقدمة في الجبر ، الجزء 2" ، Tyrtyshnikov "تحليل المصفوفة والجبر الخطي".المشكلة مع الكتب والدورات من هذا المستوى من التعقيد هي أنها موجهة من الناحية النظرية. هناك وظائف خطية ومسافات مزدوجة ، ولكن لا توجد مصفوفة إسقاط على الفضاء الفرعي وأساليب عملية لحساب القيم الذاتية. على الأرجح ، يجب استكمال الدورات من هذا المستوى بممارسة قوية ؛ على سبيل المثال ، من خلال الطرق العددية للجبر الخطي.
حول الكتاب الأخير بشكل منفصل. في رأيي ، هذا أحد أكثر الكتب الناجحة باللغة الروسية حول الجبر الخطي ، بمعنى أنه غير منفصل تمامًا عن الممارسة ؛ في الوقت نفسه ، فإنه يحتوي على جميع أنواع المواضيع "المتقدمة". إلى حد ما ، يمكن أن يحل تماما محاضرات سترانج ، ولكن يجب أن تستكمل بمهام بسيطة "لملء يدك". هناك مشاكل في هذا الكتاب ، لكنها شديدة الخطورة.
كابوس :
Kostrikin-Manin "الجبر الخطي والهندسة" ، Shafarevich-Remizov "الجبر الخطي والهندسة".بشكل عام ، هناك الكثير من الأدب الجيد باللغة الروسية ، خاصة في المستوى الأخير ، لكنه يعاني من التعقيد المفرط.
الممارسة
كما في الحالة الأولى ، الممارسة مطلوبة. اذهب SVD - تعلم ضغط الصورة. اذهب من خلال مضاعفات المصفوفة - تعلم تحويل فورييه السريع ، خوارزمية ستراسن ؛ حل العديد من المشكلات (على سبيل المثال ، من
كتب مشكلة Kostrikin أو Proskuryakov ) ؛ إرسال التحلل LU الخاص بك ، غاوس.
للأكثر ثباتًا ، يمكنني تقديم كتب رائعة عن الطرق العددية للجبر الخطي ، مثل
Trefethen ، Bau "NUMERICAL LINEAR ALGEBRA"؛ القرن ، جونسون "تحليل المصفوفة" . ستكون هذه الكتب مفيدة ، أولاً وقبل كل شيء ، في "حشو" يديك ؛ ثانياً ، سيتضح على الفور أن العديد من الطرق النظرية يتم تقسيمها إلى شرائح حول نثر الحياة (دقة الماكينة ، عدم ثبات الطرق ، العمل مع مصفوفات متفرقة).
الرياضيات المنفصلة
حوت آخر من CS الحديثة. هنا نحن مهتمون بشكل أساسي في التوافقية وأساسيات نظرية الرسم البياني.
ما تحتاج إلى معرفته من نظرية التوافقية والرسم البياني؟
معاملات ذات الحدين ، تقاربها. الرسوم البيانية أشجار البحث عن عمق واتساع ؛ تكرار العلاقات وحلولها ؛
الأدب
إحضاره على :
Anderson J. "الرياضيات المنفصلة والانسجام" ؛ Haggarti ، Schlipf J. ، Whitesides S. "الرياضيات المنفصلة للمبرمجين" ، خام O. "الرسوم البيانية وتطبيقاتها .
"يغطي أول كتابين - التلمود الممتاز في الرياضيات المنفصلة ، كل الأسئلة التي تحتاج إلى معرفتها تقريبًا.
يؤذيني كثيرا :
غراهام ، كنوت ، باتاشنيك "الرياضيات الخرسانية" ، Harari "الرسم البياني نظرية" ، خام "نظرية الرسم البياني".كابوس :
Sachkov "مقدمة في طرق اندماجي للرياضيات المنفصلة" ، Omelchenko "نظرية الرسم البياني".الممارسة
كقاعدة عامة ، يتم تضمين عدد كبير من المشاكل في الكتب المدرسية على المجموعات التوافقية. يجب حلها. في الواقع ، فإن جميع التوافقية هي فن حل المشكلات المختلفة ، وليس نظرية واحدة.