القليل من المفردات الداخلية في CPython (و PyPy)

الهيكل الداخلي للقواميس في بيثون لا يقتصر على دلو والتجزئة الخاصة وحدها. هذا هو عالم مدهش من المفاتيح المشتركة ، وتخزين مؤقت للتجزئة ، DKIX_DUMMY ومقارنات سريعة ، والتي يمكن القيام بها بشكل أسرع (على حساب خطأ مع احتمال تقريبي 2 ^ -64).

إذا كنت لا تعرف عدد العناصر الموجودة في القاموس الذي أنشأته للتو ، ومقدار الذاكرة التي يتم إنفاقها لكل عنصر ، ولماذا الآن (CPython 3.6 وما بعده) يتم تطبيق القاموس في صفيفين وكيف يتعلق الأمر بالحفاظ على ترتيب الإدراج ، أو أنك لم تشاهد العرض التقديمي بواسطة Raymond Hettinger قواميس التقاء من عشرة الأفكار العظيمة ". ثم مرحبا بك


ومع ذلك ، يمكن للأشخاص الذين هم على دراية بالمحاضرة أيضًا العثور على بعض التفاصيل والمعلومات الجديدة ، وبالنسبة للوافدين الجدد تمامًا الذين ليسوا على دراية بالدلو والتجزئة المغلقة ، ستكون المقالة ممتعة أيضًا.

القواميس في CPython موجودة في كل مكان ، والفئات ، والمتغيرات العامة ، ومعلمات kwargs تعتمد عليها ، ويقوم المترجم بإنشاء الآلاف من القواميس ، حتى لو لم تضف بنفسك أي أقواس معقوفة على البرنامج النصي الخاص بك. ولكن من أجل حل العديد من المشكلات التطبيقية ، تستخدم القواميس أيضًا ، فليس من المستغرب أن يستمر تنفيذها في التحسن ويزداد عدد الحيل إلى حيل مختلفة.

التنفيذ الأساسي للقواميس (عبر Hashmap)

إذا كنت على دراية بعمل Hashmap القياسية والتجزئة الخاصة ، يمكنك الانتقال إلى الفصل التالي.

الفكرة القواميس القواميس بسيطة: إذا كان لدينا مجموعة من الأشياء التي يتم تخزينها من نفس الحجم ، ثم يمكننا بسهولة الوصول إلى الكائن المطلوب ، مع العلم الفهرس.



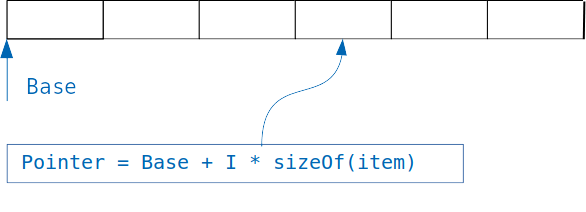
نضيف ببساطة فهرس مضروبًا في حجم الكائن إلى إزاحة المصفوفة ، ونحصل على عنوان الكائن المطلوب.

ولكن ماذا لو أردنا تنظيم عملية بحث ليس عن طريق فهرس عدد صحيح ، ولكن عن طريق متغير من نوع آخر ، على سبيل المثال ، للعثور على المستخدمين على عنوان بريدهم؟

في حالة وجود صفيف بسيط ، سيتعين علينا البحث في رسائل البريد لجميع المستخدمين في الصفيف ومقارنتها بالبحث ، وهذا النهج يسمى البحث الخطي ، ومن الواضح أنه أبطأ بكثير من الوصول إلى الكائن بواسطة الفهرس.

يمكن تسريع البحث الخطي بشكل كبير إذا حددنا حجم المنطقة التي تريد البحث فيها. وعادة ما يتحقق هذا عن طريق أخذ ما تبقى من التجزئة . الحقل الذي يتم البحث فيه هو المفتاح.



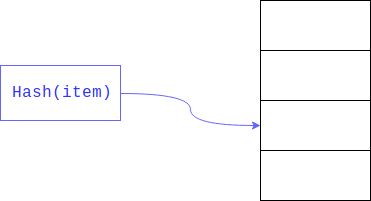
نتيجة لذلك ، لا يتم إجراء بحث خطي على المجموعة الكبيرة بأكملها ، ولكن على جانبها.

ولكن ماذا لو كان هناك بالفعل عنصر هناك؟ يمكن أن يحدث هذا بشكل جيد للغاية ، حيث لم يضمن أحد أن البقايا من تقسيم التجزئة ستكون فريدة من نوعها (مثل التجزئة نفسها). في هذه الحالة ، سيتم وضع الكائن في الفهرس التالي ، إذا كان مشغولًا ، فسوف يتحول بواسطة فهرس آخر وما إلى ذلك حتى يجد فهرسًا مجانيًا. عند استرداد عنصر ما ، سيتم عرض جميع المفاتيح التي لها نفس التجزئة.



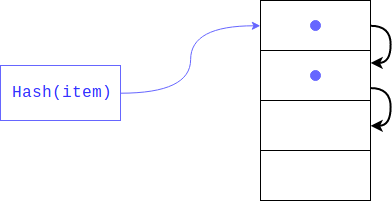
هذا النوع من التجزئة يسمى القطاع الخاص. إذا كان هناك عدد قليل من الخلايا المجانية في القاموس ، فإن هذا البحث يهدد بالانحطاط إلى خلية خطية ، وبالتالي سنخسر كل المكاسب التي تم إنشاء القاموس من أجلها ، لتجنب ذلك ، يحتفظ المترجم بالصفيف ممتلئًا في 1/2 - 2/3. إذا لم تكن هناك خلايا حرة كافية ، فسيتم إنشاء صفيف جديد أكبر مرتين من السابق ، ويتم نقل عناصر من القديم إلى الخلية الجديدة في وقت واحد.

ماذا تفعل إذا تم حذف العنصر؟ في هذه الحالة ، يتم تكوين خلية فارغة في الصفيف ولا يمكن تمييز خوارزمية البحث الأساسية ، فهذه الخلية فارغة نظرًا لعدم وجود عنصر به تجزئة في القاموس ، أو لأنه تم حذفه. لتجنب فقد البيانات أثناء الحذف ، يتم تمييز الخلية بعلامة خاصة (DKIX_DUMMY). إذا تمت مصادفة هذه العلامة أثناء بحث العنصر ، فسيستمر البحث ، وتعتبر الخلية مشغولة ، وإذا تم إدراجها ، فستتم الكتابة فوق الخلية.

ميزات التنفيذ في بيثون

يجب أن يحتوي كل عنصر من عناصر القاموس على رابط للكائن والمفتاح الهدف. يجب تخزين المفتاح لمعالجة التصادم ، الكائن - لأسباب واضحة. نظرًا لأن كل من المفتاح والكائن يمكن أن يكونا من أي نوع وحجم ، لا يمكننا تخزينهما مباشرة في الهيكل ، وهما في ذاكرة ديناميكية ، ويتم تخزين الروابط بهما في هيكل عنصر القائمة. بمعنى ، يجب أن يكون حجم عنصر واحد مساوياً للحجم الأدنى لمؤشرين (16 بايت على أنظمة 64 بت). ومع ذلك ، يقوم المترجم أيضًا بتخزين التجزئة ، ويتم ذلك حتى لا يعيد حسابه مع كل زيادة في حجم القاموس. بدلاً من حساب التجزئة من كل مفتاح بطريقة جديدة وأخذ ما تبقى من القسمة على عدد المجموعات ، يقرأ المترجم ببساطة القيمة المحفوظة بالفعل. ولكن ، ماذا لو تم تغيير الكائن الرئيسي؟ في هذه الحالة ، يجب إعادة حساب التجزئة وستكون القيمة المخزنة غير صحيحة؟ مثل هذا الموقف مستحيل ، لأن الأنواع القابلة للتغيير لا يمكن أن تكون مفاتيح القاموس.

يتم تعريف بنية عنصر القاموس على النحو التالي:

typedef struct { Py_hash_t me_hash; //  PyObject *me_key; //    PyObject *me_value; //     } PyDictKeyEntry; 

يتم التصريح عن الحد الأدنى لحجم القاموس من خلال ثابت PyDict_MINSIZE ، وهو 8.. قرر المطورون أن هذا هو الحجم الأمثل لتجنب هدر الذاكرة غير الضروري لتخزين قيم فارغة ووقت للتوسع الديناميكي للصفيف. وبالتالي ، عند إنشاء قاموس (حتى الإصدار 3.6) ، كنت بحاجة إلى 8 عناصر على الأقل في القاموس * 24 بايت في البنية = 192 بايت (هذا لا يأخذ في الاعتبار الحقول المتبقية: تكلفة متغير القاموس نفسه ، عداد عدد العناصر ، إلخ.)

تستخدم القواميس أيضًا لتنفيذ حقول الفصل المخصصة. يسمح لك Python بتغيير عدد السمات ديناميكيًا ، فهذه الديناميات لا تتطلب تكاليف إضافية ، لأن إضافة / إزالة سمة تعادل بشكل أساسي العملية المقابلة في القاموس. ومع ذلك ، فإن أقلية من البرامج تستخدم هذه الوظيفة ؛ ومعظمها يقتصر على الحقول المعلنة في __init__. ولكن يجب أن يخزن كل كائن قاموسه الخاص به ، مع مفاتيحه وتجزئةه ، على الرغم من حقيقة أنه يتزامن مع كائنات أخرى. هناك تحسن منطقي هنا هو تخزين المفاتيح المشتركة في مكان واحد فقط ، وهو بالضبط ما تم تنفيذه في قاموس PEP 412 - Key-Sharing Dictionary . لم تختف القدرة على تغيير القاموس ديناميكيًا: في حالة تغيير الترتيب أو عدد المفاتيح ، يتم تحويل القاموس من مفاتيح التقسيم إلى المفتاح العادي.

لتجنب الاصطدامات ، يكون الحد الأقصى "للتحميل" في القاموس هو 2/3 من الحجم الحالي للصفيف.

 #define USABLE_FRACTION(n) (((n) << 1)/3) 

وبالتالي ، سيحدث الامتداد الأول عند إضافة العنصر السادس.

تبين أن المجموعة تم تفريغها تمامًا ، أثناء تشغيل البرنامج ، من نصف إلى ثلث الخلايا تظل فارغة ، مما يؤدي إلى زيادة استهلاك الذاكرة. من أجل التحايل على هذا القيد ، وإذا أمكن ، تخزين البيانات الضرورية فقط ، تمت إضافة مستوى جديد من تجريد الصفيف.

بدلاً من تخزين صفيف متفرق ، على سبيل المثال:

  d = {'timmy': 'red', 'barry': 'green', 'guido': 'blue'} # -> entries = [['--', '--', '--'], [-8522787127447073495, 'barry', 'green'], ['--', '--', '--'], ['--', '--', '--'], ['--', '--', '--'], [-9092791511155847987, 'timmy', 'red'], ['--', '--', '--'], [-6480567542315338377, 'guido', 'blue']] 

بدءًا من الإصدار 3.6 ، يتم تنظيم القواميس على النحو التالي:

  indices = [None, 1, None, None, None, 0, None, 2] entries = [[-9092791511155847987, 'timmy', 'red'], [-8522787127447073495, 'barry', 'green'], [-6480567542315338377, 'guido', 'blue']] 

أي يتم تخزين السجلات الضرورية فقط ، ويتم إخراجها من جدول التجزئة في صفيف منفصل ، ويتم تخزين فهارس السجلات المقابلة فقط في جدول التجزئة. إذا كانت المصفوفة في البداية تأخذ 192 بايت ، فهي الآن 80 (3 * 24 بايت لكل سجل + 8 بايت للمؤشرات). ضغط يتحقق بنسبة 58 ٪. [2]

يتغير حجم عنصر في المؤشرات أيضًا بشكل ديناميكي ، في البداية يساوي بايت واحد ، أي أنه يمكن وضع المصفوفة بأكملها في سجل واحد ، عندما يبدأ الفهرس في الملاءمة إلى 8 بتات ، ثم تتسع العناصر إلى 16 بت ثم إلى 32 بت. هناك ثوابت خاصة DKIX_EMPTY و DKIX_DUMMY للعناصر الفارغة والمحذوفة ، على التوالي ، يحدث توسيع الفهرس إلى 16 بايت عندما يكون هناك أكثر من 127 عنصرًا في القاموس.

تتم إضافة كائنات جديدة إلى الإدخالات ، أي عند توسيع القاموس ، ليست هناك حاجة لنقلها ، كل ما تحتاجه هو زيادة حجم الفهارس وملء الفهارس بها.

عند التكرار على القاموس ، لا تكون هناك حاجة إلى مجموعة المؤشرات ، يتم إرجاع العناصر بالتسلسل من الإدخالات ، لأن يتم إضافة عناصر في كل مرة إلى نهاية الإدخالات ، يقوم القاموس تلقائيًا بحفظ ترتيب حدوث العناصر. وبالتالي ، بالإضافة إلى تقليل الذاكرة اللازمة لتخزين القاموس ، تلقينا توسّعًا ديناميكيًا أسرع والحفاظ على ترتيب المفاتيح. يعد تقليل الذاكرة جيدًا في حد ذاته ، ولكنه في نفس الوقت يمكنه زيادة الأداء ، لأنه يسمح لمزيد من السجلات بالدخول إلى ذاكرة التخزين المؤقت للمعالج.

أحب مطورو CPython هذا التطبيق لدرجة أن القواميس مطلوبة الآن للحفاظ على ترتيب الإدراج بالمواصفات. إذا تم تحديد ترتيب القواميس في وقت مبكر ، أي تم تعريفه بدقة من خلال علامة التجزئة ولم يتغير من البداية إلى البداية ، ثم تمت إضافة القليل من العشوائية إليها بحيث تختلف المفاتيح في كل مرة ، والآن أصبحت مفاتيح القاموس مطلوبة للحفاظ على الترتيب. كم كان هذا ضروريًا ، وما الذي يجب فعله في حالة ظهور تطبيق أكثر فاعلية للقاموس ولكن دون الحفاظ على ترتيب الإدراج ، غير واضح.

ومع ذلك ، كانت هناك طلبات لتنفيذ آلية للحفاظ على إعلان السمات في الفصول والأقواس ، وهذا التطبيق يتيح لك إغلاق هذه المشاكل دون آليات خاصة.

إليك ما يبدو عليه في رمز CPython :

 struct _dictkeysobject { Py_ssize_t dk_refcnt; /* Size of the hash table (dk_indices). It must be a power of 2. */ Py_ssize_t dk_size; /* Function to lookup in the hash table (dk_indices): - lookdict(): general-purpose, and may return DKIX_ERROR if (and only if) a comparison raises an exception. - lookdict_unicode(): specialized to Unicode string keys, comparison of which can never raise an exception; that function can never return DKIX_ERROR. - lookdict_unicode_nodummy(): similar to lookdict_unicode() but further specialized for Unicode string keys that cannot be the <dummy> value. - lookdict_split(): Version of lookdict() for split tables. */ dict_lookup_func dk_lookup; /* Number of usable entries in dk_entries. */ Py_ssize_t dk_usable; /* Number of used entries in dk_entries. */ Py_ssize_t dk_nentries; /* Actual hash table of dk_size entries. It holds indices in dk_entries, or DKIX_EMPTY(-1) or DKIX_DUMMY(-2). Indices must be: 0 <= indice < USABLE_FRACTION(dk_size). The size in bytes of an indice depends on dk_size: - 1 byte if dk_size <= 0xff (char*) - 2 bytes if dk_size <= 0xffff (int16_t*) - 4 bytes if dk_size <= 0xffffffff (int32_t*) - 8 bytes otherwise (int64_t*) Dynamically sized, SIZEOF_VOID_P is minimum. */ char dk_indices[]; /* char is required to avoid strict aliasing. */ /* "PyDictKeyEntry dk_entries[dk_usable];" array follows: see the DK_ENTRIES() macro */ }; 

لكن التكرار أكثر تعقيدًا مما تعتقد في البداية ، هناك آليات تحقق إضافية لم يتم تغيير القاموس أثناء التكرار ، أحدها هو إصدار 64 بت من القاموس الذي يخزن كل قاموس.

أخيرًا ، نعتبر آلية حل التصادمات. الشيء ، في الثعبان ، يمكن بسهولة التنبؤ بقيم التجزئة:

  >>>[hash(i) for i in range(4)] [0, 1, 2, 3] 

وبما أنه عند إنشاء قاموس من هذه التجزئات ، يتم أخذ باقي التقسيم ، ثم ، في الواقع ، يحددون المجموعة التي سيذهب إليها السجل ، فقط البتات القليلة الأخيرة من المفتاح (إذا كان عددًا صحيحًا). يمكنك أن تتخيل موقفًا حيث لدينا الكثير من الأشياء "ترغب" في الوصول إلى الدلاء المجاورة ، وفي هذه الحالة سيكون عليك إلقاء نظرة على العديد من الكائنات التي تكون في غير مكانها عند البحث. لتقليل عدد الاصطدامات وزيادة عدد البتات التي تحدد الجرافة التي سينتقل إليها السجل ، تم تنفيذ الآلية التالية:

  //   i = i + 1 % n //   : #define PERTURB_SHIFT 5 perturb >>= PERTURB_SHIFT; j = (5*j) + 1 + perturb; //   j % n     

perturb هو متغير عدد صحيح تهيئته بعثرة. تجدر الإشارة إلى أنه في حالة وجود عدد كبير من التصادمات ، تتم إعادة تعيينه إلى الصفر ويتم حساب الفهرس التالي بالصيغة:

  j = (5 * j + 1) % n 

عند استخراج عنصر من القاموس ، يتم إجراء نفس البحث: يتم حساب فهرس الفاصل الذي يجب أن يوجد فيه العنصر ؛ وإذا كانت الشريحة فارغة ، فسيتم إلقاء استثناء "القيمة غير موجودة". إذا كانت هناك قيمة في هذه الفتحة ، فستحتاج إلى التحقق من أن مفتاحها يطابق المفتاح الذي تبحث عنه ، فقد لا يكون ذلك ممكنًا في حالة حدوث تصادم. ومع ذلك ، يمكن أن يكون المفتاح أي كائن تقريبًا ، بما في ذلك الكائن الذي تستغرق عملية المقارنة وقتًا طويلاً من أجله. لتجنب عملية المقارنة المطولة ، يتم استخدام العديد من الحيل في Python:

  #   (   ,  C) def eq(key, entity): if id(key) == id(entity): return True if hash(key) != hash(entity): return False return key == entity 

أولاً ، تتم مقارنة المؤشرات ، إذا كان مؤشر مفتاح الكائن المطلوب مساويًا لمؤشر الكائن الذي يتم البحث فيه ، أي يشير إلى نفس منطقة الذاكرة ، ثم ترجع المقارنة على الفور إلى true. لكن هذا ليس كل شيء. كما تعلم ، يجب أن يكون للكائنات المتساوية تجزئة متساوية ، مما يعني أن الكائنات ذات التجزيئات المختلفة ليست متساوية. بعد التحقق من المؤشرات ، يتم فحص التجزئة ؛ وإذا لم تكن متساوية ، فسيتم إرجاع false. وفقط إذا كانت التجزئة متساوية ، سيتم استدعاء مقارنة صادقة.

ما هو احتمال مثل هذه النتيجة؟ حوالي 2 ^ -64 ، بالطبع ، نظرًا لسهولة التنبؤ بقيمة التجزئة ، يمكنك بسهولة اختيار مثال من هذا القبيل ، ولكن في الواقع ، لا يتحقق هذا التحقق في كثير من الأحيان؟ قام ريمون هيتنجر بتجميع المترجم الشفهي عن طريق تغيير عملية المقارنة الأخيرة بعودة بسيطة حقيقية. أي يعتبر المترجم كائنات متساوية إذا كانت تجزيئاتها متساوية. ثم وضع اختبارات تلقائية للعديد من المشاريع الشعبية على هذا المترجم الشفهي ، والتي انتهت بنجاح. قد يبدو غريباً اعتبار الكائنات ذات التجزئة المتساوية متساوية ، وليس للتحقق من محتوياتها بشكل إضافي ، والاعتماد بالكامل على التجزئة فقط ، لكنك تقوم بذلك بانتظام عند استخدام بروتوكولات git أو torrent. إنهم يعتبرون الملفات (كتل الملفات) متساوية إذا كانت علامات التجزئة متساوية ، مما قد يؤدي إلى حدوث أخطاء ، لكن منشئيهم (وجميعنا) يأملون في أن نلاحظ ، دون سبب ، أن احتمال حدوث تصادم صغير للغاية.

الآن يجب أن تفهم أخيرًا بنية القاموس ، والتي تبدو كما يلي:

 typedef struct { PyObject_HEAD /* Number of items in the dictionary */ Py_ssize_t ma_used; /* Dictionary version: globally unique, value change each time the dictionary is modified */ uint64_t ma_version_tag; PyDictKeysObject *ma_keys; /* If ma_values is NULL, the table is "combined": keys and values are stored in ma_keys. If ma_values is not NULL, the table is splitted: keys are stored in ma_keys and values are stored in ma_values */ PyObject **ma_values; } PyDictObject; 

التغيرات المستقبلية

في الفصل السابق ، درسنا ما تم تنفيذه بالفعل ويمكن استخدامه من قبل الجميع في عملهم ، لكن التحسينات لا تقتصر بالطبع على: تتضمن خطط الإصدار 3.8 دعمًا لقواميس معاكسة . في الواقع ، لا يوجد شيء يمنع بدلاً من التكرار من بداية مجموعة من العناصر وزيادة المؤشرات ، بدءًا من النهاية وتناقص المؤشرات.

مواد إضافية

لغمر أعمق في الموضوع ، يوصى بالتعرف على المواد التالية:

1. سجل التقرير في بداية المقال
2. اقتراح لتنفيذ جديد من القواميس
3. رمز مصدر القاموس في CPython