نظرية السعادة. رحلة مذهلة من شطيرة مع الزبدة

ما زلت أطلع قرّاء حبر على فصول كتابه "نظرية السعادة" بعنوان "الأسس الرياضية لقوانين المعنى". هذا لم ينشر بعد كتابًا علميًا شهيرًا ، يوضح بشكل غير رسمي كيف تسمح لك الرياضيات بالنظر إلى العالم وحياة الناس بدرجة جديدة من الوعي. إنه لمن يهتم بالعلم ولمن يهتم بالحياة. وبما أن حياتنا معقدة ولا يمكن التنبؤ بها إلى حد كبير ، فإن التركيز في هذا الكتاب ينصب أساسًا على نظرية الاحتمالات والإحصاءات الرياضية. هنا لم يتم إثبات النظريات ولم يتم تقديم أساسيات العلوم ، وهذا ليس كتابًا مدرسيًا على الإطلاق ، ولكن ما يسمى العلوم الترفيهية. لكن هذه المقاربة شبه المرحة على وجه التحديد هي التي تسمح لنا بتطوير الحدس وإلقاء المحاضرات على الطلاب بأمثلة حية ، وأخيرا ، شرح لغير المتخصصين في الرياضيات وأطفالنا ما وجدناه مثيرا للاهتمام في علومنا الجافة.



في هذا الفصل ، ندرس قانون سندويش وننظم دراسة كاملة باستخدام طريقة مونت كارلو وتحليل الأبعاد. وأخيراً ، فضح الأسطورة الشعبية التي تقول إن النفط هو سبب هذا القانون.

موضوع السقوط السقوط لا يطارد عامة الناس ولا الباحثين. لعقود من الزمان ، تم إجراء تجارب ، وتم تصوير الأفلام ، وكتابة المقالات ، وشطيرة السقوط المتضخمة مع الأساطير والاستنتاجات غير الصحيحة. لقد جذبت الكثير من المهام التي لا قيمة لها الكثير من الاهتمام ، وإذا كنت تعتقد أن كل هذا مدلِّل ، فضع في اعتبارك أنه حتى الجوائز ليست جادة أيضًا لحلها. في عام 1995 ، حصل روبرت ماثيوز على جائزة Shnobel عن عمله ، "سقوط السندوتش ، قانون مورفي ، والثوابت الأساسية" ، الذي نشر في المجلة الأوروبية للفيزياء. على الرغم من الموضوع الهزلي ورد الفعل المقابل من الأوساط العلمية ، فإن هذا المقال مثير للاهتمام تمامًا حيث يتم إجراء تحليل شامل للعملية المنزلق ويتم التوصل إلى استنتاج بعيد المدى: بغض النظر عن مخلوقات مجسمة الشكل التي تعيش في الغلاف الجوي ، سيتم محكومتها على قانون السندوتش. بعد هذا الانتصار من البحوث عديمة الفائدة ، يمكن للمرء إغلاق الموضوع ، ولكن لماذا تفوت الفرصة للنظر في طرق مثيرة للاهتمام وموضوعية كمثال لمشكلة مثيرة للاهتمام!

إيدا رمي السندويشات في مونت كارلو!

نادراً ما نرمي السندويشات مثل العملة المعدنية ، على الأقل عندما نتجاوز سن عامين. في أكثر الأحيان ، نكرر نفس التجربة بشكل لا إرادي: شطيرة ، وضعت أصلاً مع الزبدة لأعلى ، أو تنزلق من أيدينا ، أو تنزلق من على الطاولة. في عملية الانزلاق ، يلف ، يطير في الهواء ، وأخيراً ينزل على الطاولة أو على الأرض. تتأثر المرحلة الأولى من السقوط بعدد من العوامل: الاحتكاك ضد الأصابع أو سطح الطاولة ، والموضع الأولي للساندويتش وسرعته الأولية ، وارتفاع السقوط ، وأخيرا حجم السندوتش. لدينا نظام ديناميكي مع العديد من معلمات الإدخال ومخرج واحد - موقف شطيرة على الأرض. داخل النظام ، كما في حالة العملة المعدنية ، تعمل القوانين الميكانيكية ، التي توصفها المعادلات التفاضلية وهي حتمية . هذا يعني أنه لا يوجد أي حادث فيها - فالنتيجة تعتمد فقط على بيانات الإدخال ، ومع التكرار الدقيق للمعلمات ، يجب أن نحصل على نتائج مماثلة. ينطبق هذا على نموذج الساندويتش ، المقدم في شكل نظام من المعادلات التفاضلية ، ولكن ماذا عن السندوتشات الحقيقية ، الفريدة من نوعها ، التي يسقطها أناس حقيقيون في المطاعم أو في الشارع أو على الأريكة؟ يمكن وصف تباين العالم الحقيقي بتطبيق المعلمات العشوائية على مدخلات النظام الحتمية.

ومع ذلك ، فإن جبر المتغيرات العشوائية ، التي تتضمن الجمع والضرب فقط ، ليست مهمة سهلة ، ولكن لدينا معادلات تفاضلية! نحن لا نتسلق هذه البراري الرائعة ، لكننا نستخدم التقنية المتطورة في العديد من المناطق - طريقة مونت كارلو . وهو يتكون من تجميع الإحصاءات وفي تحديد خصائص نظام معقد معين نتيجة للاختبارات المتكررة ذات المعلمات العشوائية المختلفة. أؤكد مرة أخرى: النظام قيد الدراسة ليس عشوائيًا وليس فوضويًا ، ويتفاعل بشكل متوقع مع بيانات الإدخال العشوائي. في طريقة مونت كارلو ، هناك حاجة إلى العشوائية فقط من أجل فرز أكبر عدد ممكن من الخيارات بفعالية والنظر في جميع "الزوايا" الواقعية ، لاكتساب فكرة عن سلوك النظام.

في الواقع ، لقد استخدمنا بالفعل هذه الطريقة ، ومشاهدة راكبي الدراجات على تل وسوف نستمر في استخدامها من خلال ترتيب موعد نهائي في المكتب ومشاركة الأموال في مجتمع مغلق. إن المراسلات الفردية بين الاحتمال وقياس الحجم أو المساحة ، والتي تحدثنا عنها سابقًا ، تتيح لنا استخدام طريقة مونت كارلو للتكامل الرقمي. من ميزات تجربة الساندويتش القادمة أننا لن نهتم بتوزيع الاحتمالات (دقيق أو تجريبي) ، ولكن في اعتماد الاحتمالية على معلمات المشكلة. سوف نبحث عن إجابة على السؤال: تحت أي ظروف يتم تنفيذ قانون شطيرة؟ سوف نوفر العديد من المعلمات المحددة لمدخلات نظامنا الديناميكي ونجمع إحصائيات عن انخفاضات النفط لأعلى ولأسفل النفط. وبالتالي ، ستكون نتيجة سلسلة من التجارب عددًا - احتمال سقوط الزيت.

أنا مقتنع بأن إسقاط السندويشات الحقيقية على الأرض أمر خاطئ ، لذلك سوف نستخدم النمذجة الرياضية. لحل مشكلة سقوط السندوتشات ، اخترت واحدة من أجهزة محاكاة العالم المادي المتاحة والتي يتم استخدامها لإنشاء ألعاب عبر الإنترنت. سمح لإنشاء طاولة وأرضية افتراضية ، بالإضافة إلى شطرين. ظهر واحد على حافة الطاولة ، والثاني - "انزلق من أصابعه" ، أي ، انزلق من نقطة الدعم. إن قدرتي على ضبط الموضع الأولي وزاوية السندويتش ، والسرعة الأفقية (حالة تحطيم السندويتش من على الطاولة) ، ومعاملات الاحتكاك ، وحجم السندوتشات ، وارتفاع السقوط. تبدو التجارب شيئًا مثل هذا:

تجارب مع سقوط السندويشات الافتراضية في محاكاة للعالم المادي.

في اللحظة التي يلمس فيها الساندويتش الأرضية ، تكون زاوية السندويتش ثابتة ، أو بالأحرى ، زاوية المتجه طبيعية فيها. سوف تخبرنا علامة جيب هذه الزاوية عن الجانب الذي تحول النفط منه: حالة ناجحة تتوافق مع قيمة موجبة ، والموقف الهابط يتوافق مع قيمة سالبة. يتم إدخال النتيجة في الجدول ، وساندويتش الظاهري الجديد جاهز للسقوط. المهمة التي حددناها هي: تقييم احتمالية سقوط شطيرة الزيت عند سقوطها من ارتفاع معين.

تفترض طريقة مونت كارلو أن المتغيرات العشوائية تستخدم كمعلمات. وهنا يجدر القول بضع كلمات حول ما هو متغير عشوائي . دعنا نعود إلى علماء الرياضيات والهياكل الرياضية. ما هو الهيكل الذي يمكن استخدامه لمحاكاة نتائج سقوط الرقم على الزهر ، أو مستوى الماء في النهر ، لأن هناك إثارة مستمرة على الماء؟ كيف تتعامل مع عدد السيارات التي تجتاز التقاطع خلال ساعة؟ ما الهيكل الذي يمكن أن يصف حالة الإلكترون؟ من ناحية ، هذه أرقام محددة من مجموعة محددة من القيم: للعظم ، على سبيل المثال ، من مجموعة $$$\ {1،2،3،4،5،6 \}$ ، ومن السهل الحصول على هذه القيمة عن طريق إجراء تجربة. ومع ذلك ، فإن التجربة الثانية سوف تعطي نتيجة مختلفة ، من الواضح أن هذا ليس مجرد رقم: اليوم هو واحد ، وغدا هو آخر. قد ينشأ سؤال فلسفي: هل من المنطقي التحدث عن بعض القيمة الدقيقة "لمستوى الماء في النهر" ، أو عدد السيارات ، لأنه لا يمكن "اكتشاف" هذه القيم وتسجيلها؟ هل يمكن أن يكون هناك ، بأي حال من الأحوال ، معرفة دقيقة لمتغير عشوائي؟

في كثير من الأحيان ، عند الحديث عن مثل هذه المتغيرات العشوائية ، فإنها تقتصر فقط على القيمة المتوسطة ، ولكن هذه طريقة رائعة للتشويش أو حتى الخلط المتعمد. رقمان: المتوسط ​​والانحراف المعياري ، أفضل بالفعل ، ولكن من الواضح أن هذا ليس كل المعلومات حول موضوع الاهتمام بالنسبة لنا. ربما هذه ليست أرقام ، ولكن مجموعات؟ قل ، يمكنك محاولة وصف مستوى المياه في النهر كفاصل زمني للقيم المحتملة ، مع مراعاة الإثارة ، وكمثال على السيارات ، قل أن ما بين 1 و 100 سيارة تمر في ساعة ، إلخ. لكن من السهل أن نرى أن مجموعة القيم الممكنة ليست كافية أيضًا ، على سبيل المثال ، مع التكرار المتكرر لقياس عدد السيارات في الشارع ، ستحدث بعض الأرقام في كثير من الأحيان ، والبعض الآخر لن ننتظره على الإطلاق. في الفصل الأخير ، قدمنا ​​مقياس الاحتمال كدالة على فضاء الاحتمال. بالنسبة للكمية العشوائية ، ستكون الأحداث الأولية لهذه المساحة هي عناصر مجال التعريف الخاص بها ، ويحدد المقياس توزيع الاحتمال لهذه الكمية. والآن هذه هي معلومات شاملة ودقيقة. يمكن تمثيل الوظيفة بشكل تحليلي أو تقريبي بوظيفة أخرى ، في شكل جدول أو رسم بياني أو في شكل رسم بياني. كل هذه التمثيلات هي نماذج لنفس الكائن - متغير عشوائي ، وأهم شيء هنا ليس هو النوع المحدد من التمثيل مثل الخصائص الرياضية لهذه الوظيفة. بالنسبة لتوزيعات الاحتمال ، تختلف الخصائص: عدد المعلمات ، وعدد الأنماط ، والنتروب ، والقسمة اللانهائية ، والإضافة ، والاستقرار ، والتكامل ، وما إلى ذلك. إن وضع نموذج لمتغير عشوائي غير معروف تم الحصول عليه من التجربة ، وإحصائيات من ترسانة ضخمة من التوزيعات المعروفة ذات الخصائص المحددة بدقة ، لا تحدد الوظيفة "الأكثر تشابهًا" ، بل الوظيفة التي تتوافق تمامًا في خصائصها مع المتغير العشوائي المرصود. هذا هو جوهر التحليل الإحصائي وتقنيات اختبار الفرضيات الإحصائية المألوفة لدى كل طالب قام بلمس الإحصاءات.

لدينا الآن مشكلة ، إلى حد ما ، العكس. نحتاج إلى تعيين معلمات الساندويتش مع متغيرات عشوائية ، وعدم وجود بيانات إحصائية ، ولكن تسترشد الخصائص الضرورية لهذه الكميات. هذا جزء مهم ومثير للاهتمام من طريقة مونت كارلو ، التي يعتمد عليها كل من الحل وصحتها.

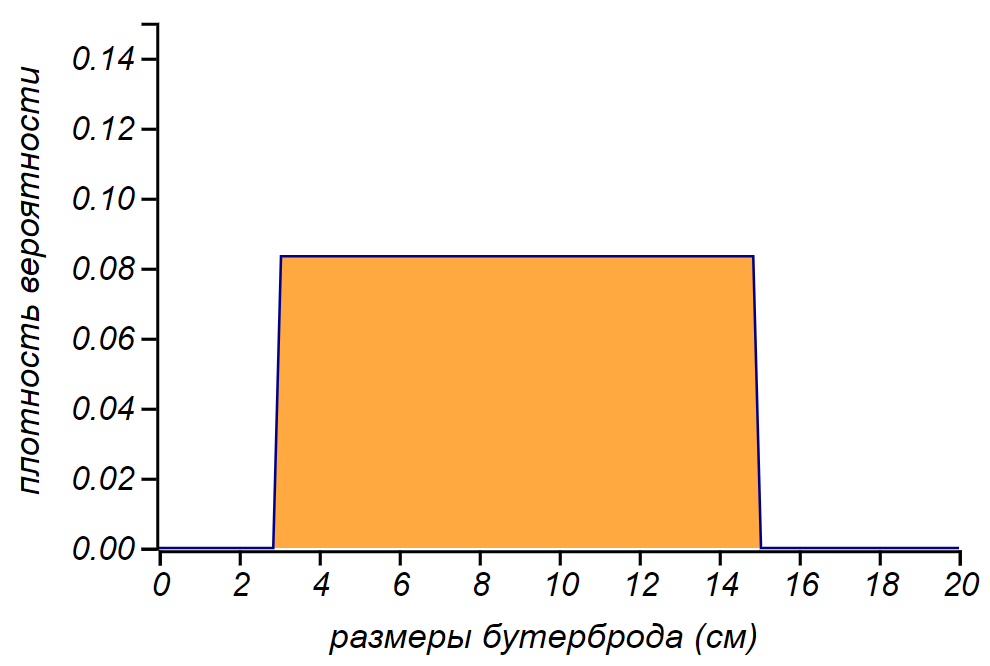1. أبعاد شطيرة. ماذا يمكن أن يكون؟ canapes الحجم معقول لديه سنتيمتر $$ واسعة ، وطالب جيد "اللحاء" يمكن أن يكون سنتيمتر $$ . في معظم الأحيان ، السندويشات لها أحجام من $$ قبل $$ انظر في هذه الحالة ، فإن احتمال مواجهة شطيرة بعرض ملليمتر أو متر ، بالمعنى العملي ، هو صفر. لا أستطيع أن أقول أي شيء أكثر عن السندويشات وسأقبل حجم السندويشات الموزعة بالتساوي في النطاق المحدد. الخيار غير كامل ، ومع ذلك نجد السندوتشات العادية أكثر من السندويشات الضخمة أو العملاقة. ولكن في وقت لاحق سنرى أن هذه النقطة الضعيفة يمكن التحايل عليها بأمان.

2. انطلاق الموقف. هنا ، دون مزيد من اللغط ، سنضع توزيعًا موحدًا لتحريك الساندويتش على حافة الطاولة ، إذا سقط فقط.

3. معامل الاحتكاك. هذه كمية لا تحتوي على أبعاد ، وهذا يتوقف فقط على المادة. الطاولات وأغطية المائدة مختلفة ، والأصابع تضغط على شطيرة بنقاط قوة مختلفة. مجموعة معامل من $$ قبل $$ في حين أن القيم القصوى غير محتملة ، في المتوسط ​​، يمكنك توقع شيء ما $$ . أي توزيع غير متماثل على شكل جرس له قيمة غير سالبة ، على سبيل المثال ، توزيع غاما أو سجل طبيعي ، سوف يساعدنا.

4. السرعة الأولية. نادراً ما نطلق السندويشات بسرعة عالية ، وفي أغلب الأحيان لا نرميها على الإطلاق ، لكن هذا يحدث بالفعل. كل ما هو معروف عن حجم السرعة هو أنها إيجابية ويمكن افتراض أنه عند التمرير ، في المتوسط ​​، نتحرك كأيدي متوسطة ، أي بسرعة $$ م / ث إذا كان هذا معروفًا فقط عن الكمية ، فمن المعقول وصفها من خلال التوزيع الأسي (لماذا ، سنتحدث لاحقًا عندما نتعرف على إنتروبيا التوزيعات). وضعه هو صفر ، وبالتالي فإن نسبة السندويشات التي سقطت دون سرعة أولية كبيرة ستكون لائقة جدا. في "الذيل" سوف تكون السندويشات ، يتم إطلاقها عن غير قصد أثناء الطيران عند خفق الفتات من الطاولة.

5. سنصلح ارتفاع الجدول ، وسنسقط منه مئات السندوتشات ، ونحسب عدد الزيت الساقط لأسفل ونضعه في الجدول ، أو نعكس احتمال الارتفاع على الرسم البياني.

فيما يلي احتمالات إسقاط شطيرة بالزبدة:

احتمالية هبوط السندوتشات السندوتشات المختلفة مع ظروف مختلفة حسب ارتفاع السقوط. لكل ارتفاع $$ الاختبارات.

بعض الميل واضح ، ولكن انتشار واسع للغاية قد انتهى. عند المتوسط ​​، اتضح أن احتمال ارتفاع السقوط مستقل تقريبًا وبالكاد يتجاوز النصف. هل يمكنك الوثوق بهذه التجربة؟ هل يدحض قانون شطيرة؟ ربما لم نرسم السندويشات بشكل كافٍ - كان هناك الكثير من البيانات المزعجة! دعنا نزيد عدد الرميات ونرى ما سيحدث:

احتمالية هبوط الزيت في شطائر مختلفة محسوبة لعدد أكبر من الاختبارات (500 لكل ارتفاع).

يوجد عدد أقل من الانبعاثات ، لكن من الواضح بدرجة أكبر أن قانون السندوتش ضعيف للغاية. لكن هل أجرينا تجاربنا بشكل صحيح؟ تبدو طريقة مونت كارلو بسيطة للغاية: اعرف نفسك بديلاً عن البيانات الرهيبة وشاهد ما يحدث. الرياضيات شيء صادق: أي نوع من الأسئلة هي مستعدة لتقديم أي نوع من الإجابة . ولكن ما إذا كانت هذه الإجابة منطقية يعتمد على السؤال.

قبل البدء في التجارب ، وليس مثل لعبة لدينا ، ولكن حقيقية ومكلفة ، باستخدام الأقمار الصناعية التي تدور حولها ، أو مسرّع الجسيمات أو ألف شطائر حقيقية بالزيت ، من الضروري القيام بالأعمال التحضيرية. وإحدى الطرق القوية والجميلة لفهم كيفية إجراء تجربة بشكل صحيح هي تحليل أبعاد المشكلة.

صممنا شطيرة من خلال الإحداثيات المعممة ، الزخم والقوى - الكميات الفيزيائية ، والتي ، بدورها ، ترتبط بواسطة معادلات الميكانيكا التحليلية. في الفيزياء ، الكميات الكمية التي نتعامل بها ، والتي نقيسها ونستبدلها في المعادلات ، لا "تنسجم" مع الأعداد العادية - بل لها بنية إضافية تسمى البعد . ليست كل التعبيرات الرياضية الصحيحة منطقية إذا كانت الكميات البعدية تشارك فيها. دعنا نقول أنه لا معنى لإضافة السرعة والكتلة ، فمن المستحيل مقارنة القوة والمسافة. ومع ذلك ، يمكننا النظر في نتاج السرعة والكتلة ، بعد تلقي كمية جديدة من الأبعاد - الزخم ، أو الزخم ؛ من الممكن ضبط السرعة والقسمة على المسافة ، وبالتالي الحصول على قيمة لها بعد التسارع.

وُلد تحليل البعد ونظرية التشابه منذ زمن طويل ، منذ عهد اللورد رايلي. يتم استخدامها في الميكانيكا ، والديناميكا الكهربائية ، والفيزياء الفلكية وعلم الكونيات ، مما يجعل من الممكن التعامل مع المهام المعقدة بأناقة مخيفة. ومع ذلك ، لم يتم الانتهاء من البحث في هذا المجال ، ولم يقدم عالم الرياضيات الأسباني الفارو رابوسو تعريفًا دقيقًا للهيكل الذي تشكله الكميات الكمية (الأبعاد) إلا في عام 2016.

غالبًا ما ينظر الطلاب والطلاب إلى القيود التي تفرضها الأبعاد على الصيغ المادية على أنها فوضى إضافية تحتاج إلى مراقبتها. ولكن من ناحية أخرى ، فإن القيود الثابتة منطقيا مفيدة للغاية! يقومون بتصفية التعبيرات غير الصحيحة ، ويسمحون لك "بالتنبؤ" بهيكل حل المشكلة المادية قبل حلها المفصل ، فهي أداة قوية في تخطيط وتحليل البيانات التجريبية.

لكن هذا مثير للاهتمام. حسبنا سقوط الشطيرة في البرنامج ، باستخدام أرقام غير عادية ولكن عادية. كيف يمكن للمرء "مسح" كمية مادية من بعد وتحويله إلى رقم؟ لهذا الغرض ، نحن على دراية بوحدات قياس الكميات الفيزيائية المألوفة: كل هذه العدادات ، الجنيهات ، الدقائق ونيوتن. تأخذ وحدات القياس الجزء الأبعاد من الكمية ، مما يتركنا مع عامل - رقم حقيقي ، يمكن للكمبيوتر التعامل معه بالفعل. على سبيل المثال ، السرعة في الاتجاه المحدد هي $$ كم / ساعة يمكن أن يمثلها الرقم $$ . ولكن هناك دقة: يعتمد التمثيل العددي على اختيار وحدات القياس. إذا قمت بتحديد وحدات أخرى (على سبيل المثال ، أمتار وثواني) ، فسوف يتم تمثيل نفس السرعة برقم مختلف: $$ . الأرقام مختلفة ، ولكن الكمية واحدة ، ولا تعتمد على اختيارنا لأي وحدات.

السؤال الذي يطرح نفسه: هل هناك بأي حال نظام "أفضل" للوحدات؟ اتضح أنه ، لهذا ، عند حل المشكلة ، من الضروري استخدام الكميات الأبعاد المضمنة في المشكلة كوحدات قياس.

في هذا الفصل ، لدينا شطائر تطير ، في العملات السابقة التي تطير واحدة ، نعطي مثالاً آخر على الطيران. كيف ينبغي مقارنة صفات طيران الطيور المختلفة؟ من الواضح أن السرعات التي تتطور بها الطيور مختلفة: بالنسبة للحمام - $$90 كم / ساعة على الطريق السريع -$90$$$140 كم / ساعة ، للرافعات والعصافير أو اللافتات -$140$$$50 كم / ساعة ، للطيور الطنانة -$50$$$80 كم / ساعة لكن كل هذه الطيور تختلف اختلافا كبيرا في حجم وطريقة الرحلة. إذا تم قياس طول الببغاء في الببغاوات ، وتم قياس الوقت في فترات ترفرف بجناحيه ، يمكنك الحصول على بعضالسرعة الخاصة، كما يقولون. يمكنك تقسيم السرعات التي يمكن أن تتطور بها هذه الطيور إلى قيم متناظرة والحصول على سرعة بدون أبعاد تُبيِّن المدة التي يمكن للطائر أن يسافر بها في رفرف واحد من أجنحته. هذه هي نتيجة هذه المقارنة:$80$

الطائر	السرعة ، كم / ساعة	طول الجسم	تردد الاجتياح ، 1 / ​​ثانية	, /
	140	18	5	0,9	43
	90	30	5	1,5	17
	80	8	200	16	1,4
	50	1	2،5	2،5	5
	50	40	9	3.6	3,8
	46	12	13	1,6	8

يمكن ملاحظة أن هذا النوع من الطيور السريعة يعتبر بحق أفضل نشرة ، لكن طائر الطنان يستهلك طاقة غير فعالة ، ومع ذلك ، فإن هذا الطائر ليس لديه مشكلة في الطيران لفترة طويلة ، مثل الحمامة. تختلف نفس السرعات المطلقة للرافعة والعصفور والبط بشكل كبير عند ترجمتها إلى كميات بدون أبعاد. يستخدم هذا النوع من الحسابات لمحاكاة طائرة كبيرة حقيقية ، واختبار نموذج صغير في نفق الرياح. إذا كانت جميع المعلمات البعدية لهذين النظامين متقاربة ، فيمكن اعتبارهما متشابهين جسديًا والنمذجة منطقية. لقد استخدمنا هذا النهج بالفعل ، مما يعكس الوحدات النسبية بدلاً من الوحدات المطلقة على مخططات لورنز. هذا سمح لنا للمقارنة بين مختلف الظواهر والتوزيعات.

من الواضح ما سيكون أنسب نظام للوحدات عند تحليل رحلة الشطيرة. بالطبع ، يجب قياس الطول في السندويشات. لكل وحدة زمنية ، يمكنك أن تأخذ القيمة$$√ل / ز أين$\sqrt{l/g}$$$ل هو طول شطيرة ، و$l$$$g هو تسارع الجاذبية. ولا ينبغي أن يقاس ارتفاع الجدول بالأمتار ، ولكن بوحداته الخاصة. بعد الحصول على النتيجة ، يمكننا تعميمها فورًا على حالة العلب و "حذاء الحذاء" الصلب. لذلك ، نكرر الحسابات ، لكن على الرسم البياني نعكس ارتفاع الجدول بالوحدات النسبية. إذا فعلنا كل شيء بشكل صحيح ، فحين حصلنا على شطرين مختلفين الحجم ، يجب أن نحصل على رسومات متشابهة للغاية. دعونا التحقق من ذلك:$g$

احتمال سقوط شطيرة زيت أسفل قيمة ثابتة معينة ، على ارتفاعات مختلفة للوقوع ، محسوبة بالوحدات النسبية. تتوافق النقاط الزرقاء مع شطيرة بحجم 5 سم ، ونقاط حمراء تتوافق مع 10 سم ،

وفي الصيغة الأولية ، قمنا بفرز مختلف الأحجام وتلقينا سحابة من النتائج التي تم فيها إخفاء الاعتماد على الاهتمام بالنسبة لنا. مع زيادة عدد الاختبارات ، قمنا بتقييم هذه السحابة وتلقينا إجابة غير مفيدة. لكي نوضح بشكل أوضح ماهية الخطأ المنهجي ، تخيل أننا نريد حساب احتمالية سقوط شطيرة بالزبدة ، مع مراعاة الظروف والأحجام الأولية للساندويتش والارتفاع. هذا يعادل متوسط ​​النتائج التي حصلنا عليها في وقت واحد. نتيجة لذلك ، لدينا أرضية وسط ثقة - احتمال قريب جدًا من$$1 / 2 ، كما هو الحال في إرم عملة! هذه نتيجة منطقية ومتوقعة للغاية ، لكنها غير مفيدة تمامًا. من خلال حساب الكثير من البيانات بأحجام مختلفة ، نحن بالفعل على وشك الانتهاء من هذا الاستنتاج. ولكن إذا كان الغرض من النمذجة هو تحديد الأنماط ، فمن المنطقي تقليل عدد المعلمات. البيانات التي تم مسحها الآن تتحدث بوضوح عن تأييد لقانون العبث ، وتقتصر ، مع ذلك ، على مجموعة معينة من المرتفعات: من$1/2$

$$2 إلى$2$$$$6$ حجم شطيرة (من ارتفاع الكوع فوق الطاولة إلى ارتفاع ذراعي شخص يقف). خارج هذا النطاق ، لدى الساندويتش فرصة أكبر في قلب الجانب الأيمن قبل السقوط.

ولكن ماذا لو نظرت إلى أبعد وألقيت السندويشات من النافذة؟ من الواضح أنه عند السقوط من ارتفاع كبير ، لا يهم أي جانب يقع في ما ستتحول إليه الساندويتش ، وتستقر مقاومة الهواء في السقوط ، لكن من الناحية النظرية ، ماذا نتوقع أن نرى؟ ربما ، ينبغي ملاحظة بعض التقلبات في الاحتمال مع زيادة وقت الرحلة. لنرى:
احتمالية هبوط شطيرة الزيت عند السقوط من ارتفاع عالٍ.

خمننا التردد ، لكن من الغريب أن تتناقص السعة ، وتقلبت الاحتمالات إلى $$ . ما الذي يمكن أن نتحدث عنه؟ هل هذا هو نفس التأثير الذي يحدث في حالة العملة المعدنية ، عندما تصبح زيادة انحرافات الظروف الأولية أكثر أهمية مع زيادة مدة الرحلة؟ اتضح في هذه الحالة أن طبيعة معادلة الاحتمالات مختلفة.

تحليل الأبعاد أكثر قليلا

بغض النظر عن مدى تافه موضوع كتابنا ، فنحن نتحدث لغة الرياضيات ، وهو يناضل من أجل حلول دقيقة. سمحت لنا طريقة مونت كارلو بالحصول على فكرة عن الحل ، لكن هذا ما يسمى بالقوة الغاشمة. هذا ليس مثيرا للاهتمام مثل بعض على الأقل ، ولكن الحل التحليلي. سيسمح لنا تحليل الأبعاد بالحصول على شكل نظري للاعتماد الذي تم الحصول عليه بواسطة طريقة مونت كارلو. لهذا ، لا نحتاج إلى حل المعادلات التفاضلية ؛ علاوة على ذلك ، فإن جميع اعتباراتنا لا تتجاوز حدود العلاقات البدائية والواضحة تمامًا. هذا هو سحر التحليل الأبعاد ، والذي يبدو في بعض الأحيان وكأنه خدعة. لذلك دعونا نبدأ ، بتقييد أنفسنا من أجل البساطة إلى الانزلاق فقط شطيرة من الطول $$$ل$ من الجدول الارتفاع $$$H$ مع الصفر السرعة الأفقية.

1. زاوية دوران شطيرة السقوط تعتمد على الوقت والسرعة الزاوية:

$$

$$\ varphi = t \ omega.$$

2. السرعة الزاوية تساوي ناتج الوقت المنزلق والتسارع الزاوي:

$$

$$\ omega = t_0 \ varepsilon.$$

3. يمكن التعبير عن وقت الانزلاق من حيث تسارع الجاذبية وجزء من طول الساندويتش الذي كان ملامسًا للجدول بالنسب التالية:

$$

$$t_0 \ propto \ sqrt {\ frac {l_0} {g}}.$$

هنا $$$l_0 دولا$ - طول شطيرة ملقاة على الطاولة. هنا نستخدم علاقة التناسب المشار إليها بواسطة العلامة $$$\ propto$ . التعبير $$$y \ propto x$ يمكن استبداله بـ $$$y = C x$ اين $$$C$ - بعض ثابت غير معروف. أنا حقا أحب هذا الموقف. التناسب "يدمج" كل شيء معقد يتحول إلى ثابت: كل من حقيقة أن لحظة الجاذبية تتغير أثناء الدوران ويتغير مركز الدوران عند الانزلاق. كل هذا ، بالطبع ، تحتاج إلى معرفته لحساب دقيق ، لكن النتيجة ليست سوى معامل بدون أبعاد ، وفي تحليلنا لا تلعب دورًا. بأيقونة واحدة ، أنقذنا أنفسنا من التكامل الممل.

4. يحدث التسارع الزاوي من تسارع الجاذبية ويعتمد على الكتف الذي يتم تطبيق الجاذبية عليه:

$$

$$\ varepsilon \ propto \ frac {g} {l-l_0}.$$

ومرة أخرى علامة $$$\ propto$ سمح لنا بعدم حساب لحظة القصور الذاتي للوحة للمحور الكامن في مستواها ، وكذلك الإسقاط المتغير للجاذبية (هذان هما تكاملان آخران).

5. أخيرًا ، يعتمد وقت السقوط على ارتفاع الطاولة وتسارع الجاذبية:

$$

$$t \ propto \ sqrt {\ frac {H} {g}}.$$

6. استبدال كل هذه التعبيرات في الصيغة الأولى ، نحصل على نتيجة بسيطة:

$$

$$\ varphi \ propto \ sqrt {\ frac {l_0 H} {l (l-l_0)}} ،$$

الذي ، إذا قمت بقياس جميع أطوال السندويشات ، يتحول إلى

$$

$$\ varphi \ propto \ sqrt {\ frac {x h} {1-x}}.$$

هنا $$$l_0 = x l$ و $$$H = ح ل$ . حسنًا ، كل شيء يتقارب - الزاوية لا تحتوي على أبعاد وتعتمد على المعاملات التي لا تحتوي على أبعاد. هذه الزاوية لا تعتمد على المقياس الزمني ؛ تبقى هندسة خالصة. المقام ليس خطرا عندما $$$×> 0.5 دولا$ لن تسقط الساندويتش على الإطلاق (نحن ندرس الصفر السرعة الأفقية) ، لذلك $$$0 <x <0.5 دولا$ .

يتم تحديد أي جانب يسقط السندويش بواسطة علامة جيب الزاوية $$$\ varphi$ أي وظيفة $$$\ mathrm {sign} (\ sin \ varphi)$ . هذه الوظيفة تعود $$$-1 دولا$ لحالة "النفط يصل" و $$$1$ ل "النفط أسفل". يمكننا استخدام هذه الوظيفة للتعبير عن احتمال سقوط شطيرة حتمية إذا وصلنا إلى مجموعة من $$$0$ قبل $$$1$ :

$$

$$P _ {\ downarrow} (x، h) = \ frac12 \ left [1+ \ mathrm {sign} (\ sin \ varphi) \ right] = \ frac12 \ left \ {1+ \ mathrm {sign} \ left [ \ sin \ left (C \ sqrt {\ frac {xh} {1-x}} \ right) \ right] \ right \} ،$$

حيث يشير السهم رمزياً إلى موضع الزيت. معامل $$$C$ الذي يظهر في صيغة الاحتمال يعبر عن كل ما يظل مخفيًا بمساعدة علامة التناسب. لقد كانت بالفعل خطوة صعبة للغاية ، لقد أنقذتنا من التكامل الممل (وحتى ثلاثة) ، لكن كيف يمكننا الآن معرفة ما الذي يساويه هذا المعامل؟ من التجربة ، علاوة على ذلك ، تجربة واحدة مع قياس الزاوية في وقت السقوط كافية للحصول على تقدير لهذه القيمة! باستخدام جهاز محاكاة ، وجدت بسهولة ذلك $$ .

المهمة التالية هي التعبير عن المواقف الأولية رياضيا $$$x$ قد يكون مختلفا. نحن مهتمون باحتمالية سقوط شطيرة بالزبدة إذا $$$x$ سوف تكون متساوية $$ او $$ أو أي رقم من $$$0$ قبل $$ . استخدمنا الاتحاد "أو" ، واعتبرنا كل حالة من هذه الحالات مستقلة وتستبعد جميع الحالات الأخرى في تجربة محددة. تذكر أن الاحتمال هو مقياس لمساحة الاحتمال ، وإذا كان الأمر كذلك ، فإن الاحتمال يكون مضافة. هذا يتيح لنا ببساطة إضافة الاحتمالات $$$P _ {\ downarrow} (x، h)$ ، لجميع القيم $$$x$ ، ضرب من قبل من قبل احتمال الوقوع في مجموعة محددة من القيم. نحن كسر هذا الجزء من $$$0$ قبل $$ على $$$ن$ أجزاء ، وحساب تقدير الاحتمال في شكل مبلغ:

$$

$$P _ {\ downarrow} (h) \ sim \ frac {2} {n} \ sum \ limit_ {i = 0} ^ n P _ {\ downarrow} \ left (\ frac {i} {2n} ، h \ right ) ،$$

هنا المضاعف $$$2 / ن$ يعبر عن احتمال متغير عشوائي $$$x$ ندخل قطعة من العرض $$$1 / ن$ . إليك ما تبدو عليه النتيجة بالنسبة لعدد كبير من الأقسام ( $$$ن = 100 دولا$ ) وسلسلة من التجارب العددية مع السرعة الأفقية صفر:

التقييم النظري والتجريبي لاحتمال سقوط زيت لشطيرة عند سقوطها من ارتفاع كبير. السرعة الأفقية الأولية في التجارب هي صفر.

يحتوي الحل الذي قدمناه من قبل على المزيد من المعلمات العشوائية ، وبالتالي فقد أصبح أكثر سلاسة وأقرب $$ . ولكن ، من حيث المبدأ ، يمكن إجراء تحليل الأبعاد لحالة أكثر عمومية.

يرجى ملاحظة أن الاحتمال $$$P _ {\ downarrow}$ تقترب مع زيادة $$$ح$ لقيم قريبة من $$ . وهذا ليس على الإطلاق بسبب عدم اليقين وتأثير الأخطاء الأولية. أظهرت الحسابات أن هذا هو نتيجة لإضافة العديد من التوافقيات التي شكلتها القيم $$$x$ عند الجمع $$$P _ {\ downarrow} (x، h)$ . إذا نسينا ساندويتش مؤسف ومواصلة الجدول الزمني $$$P _ {\ downarrow}$ ، ثم نرى أن تقدير الاحتمال سيستمر في التقلب الشديد $$ ، والسعي تدريجيا لهذه القيمة.

هل من الممكن معرفة دون حسابات مباشرة ما إذا كان الاحتمال سيستمر في التقارب $$ أم أنها سوف تنمو مرة أخرى؟ وفي هذه الظاهرة يوجد أيضًا مكان للرياضيات غير التافهة والعميقة. الحقيقة هي أن كل قيمة $$$x$ يتطابق تردد معين من التذبذبات ، وتشكل المجموعة بأكملها الطيف المزعوم للوظيفة الكلية. إذا كان الطيف منفصلًا ، أي يتكون من ترددات منفصلة ، فستكون الوظيفة الكلية (يطلق عليها تحويل فورييه) دورية. إلى الطيف المستمر في شكل ثابت على قطعة من $$$0$ قبل $$ وظيفة aperiodic المقابلة لتذبذبات سوف تتوافق. لكننا نظرنا إلى فرع جديد من الرياضيات - التحليل الوظيفي .

علم كبير إنريكو فيرمي ، جد طريقة مونت كارلو (عالم الرياضيات ستانيسلاف أولام ليكون الأب) ، أن يقوم طلابه بتقييمات بسيطة ، ومعرفة قطعة من الورق أو الأصابع ، والتي نتوقع الحصول عليها قبل متابعة الحل الدقيق للمشكلة. إنه لأمر رائع أنه إذا تبين أن التقييم صحيح ، فسوف يتضح أن جوهر المشكلة قد تم التقاطه ، وإذا لم يكن كذلك ، فهذه هي النتيجة الأكثر فائدة - وهذا يعني أن المهمة تبين أنها أكثر إثارة للاهتمام مما يبدو!

في حالتنا ، تقدير بسيط يكفي ؛ مشكلة شطيرة لا يستحق حل أكثر شمولا. أظهرت طريقة مونت كارلو تلميحات فقط من الحل ، وأظهر تحليل الأبعاد فقط بعض من هيكلها العام ، ولكن معا يمكن أن تظهر لنا كيف يعمل الاحتمال المطلوب. يتيح الإطلاع على عالم الرياضيات رؤية بنى جاهزة في مخططات الحل ووضع افتراضات واستنتاجات بعيدة المدى.

استخدم روبرت ماثيوز ، في دراسته التاريخية ، تحليل الأبعاد لإظهار أن قانون شطيرة أمر أساسي. يعتمد استنتاجه على حقيقة أن الحد الأقصى لارتفاع الكائن الحي الذي وصل إلى أطرافه الخلفية بهدف أخذ مقدمة القدم إلى أخذ شطيرة بالزيت تحددها خصائص قوة الأنسجة البيولوجية والجاذبية. بالمقابل ، يجب أن يتوافق الحجم المميز للشطيرة مع حجم المخلوق - والأقزام الموجودة على بعض الكوكب الثقيل والدويلد على كوكب ذي خطورة منخفضة ستختار السندوتشات لنفسها في الحجم. هنا نأتي إلى ما يسمى المضاربة في العلوم. هذا ليس إعادة بيع لأي سلعة بأسعار باهظة ، ولكن الافتراضات المشكوك فيها التي تشكل أساس البناء المنطقي. على وجه الخصوص ، نفترض أن المخلوقات لها أيد لها أبعاد مماثلة لأجلك ، وهذا أكثر من قابل للنقاش.

عن النفط والرياح

في ميرفولوجيا ، الاقتباس غير صحيح لقانون X.L. مجموعة منكا:

دائمًا ما يكون للمشاكل المعقدة حلول بسيطة وسهلة الفهم وغير صحيحة.

يمكنك أن تسمع في كثير من الأحيان أن قانون السندويش يقع على عاتق النفط ، وهو أكثر كثافة من الخبز وبالتالي "يفوق". وعلى الرغم من أن هذا لا ينطبق على موضوع كتابنا ، إلا أنني أريد تحليل هذا السؤال من أجل وضع حد له. بحيث يمكن لأي شخص في وقت لاحق الرجوع إلى حقيقة أن "العلماء أثبتوا أن وجود النفط لا يؤثر على أي جانب من الصفعات ساندويتش!"

عندما كنا طفلاً ، شعرنا بالارتياح من خلال رمي ذبابة الحمام أو ريشة الذيل ، عالقة في قطعة من البلاستيسين ، أو سنتيمتر أو قطرها ، على ارتفاع. طار ما يصل إلى أربعة أمتار ، وبعد ذلك نزل بشكل جميل وسلس في التشغيل التلقائي ، مثل طائرة هليكوبتر مع محرك مكتوم. ثم نشأنا ، وأصبح المرح لدينا أقل ضررا. لقد حصلنا على الجوز وقمنا بربط براغي به من الجانبين المتقابلين ، وضغطنا على الحشوة من رؤوس المطاحن المكسرة. بقي لربط شريط أو مجرد قطعة من الحبل بأحد البراغي ، لفكها بشكل صحيح والركض في السماء لمدة خمسة عشر متراً. في الخريف ، استقر الشريط الخفيف على الوضع الرأسي للقذيفة ، مما يوفر تأثيرًا عالي الجودة على الأسفلت وانفجارًا صغيرًا ، وفي بعض الأحيان تمزق الجوز إلى قطع. (كن حذرًا إذا قررت مشاركة تجربة الطفولة هذه مع أطفالك!)

في كلتا التجربتين ، نرى أن القلم أو الشريط الخفيف سرعان ما ظهر فوق الجزء الثقيل من الجهاز واستقر السقوط. هذا ، على ما يبدو ، يؤدي إلى رأي بديهي مفاده أن الزبدة الثقيلة والخبز الخفيف يجب أن تتصرف أيضًا بهذه الطريقة. تخيل بالون: توجد سلة كثيفة تحت بالون أقل كثافة. علاوة على ذلك ، تشير التجربة إلى أنك إذا فهمت بإصبعين الوسط الهندسي لكائن ذي كتلة موزعة بشكل غير متماثل ، فسوف تتعثر حتى يصبح الجزء الثقيل في الأسفل.

لكن كلتا هاتين الظاهرتين لا تعملان في حالة السندوتشات الساقطة.

لنبدأ بالعملية الثانية - بـ "التفوق". لم يكن من قبيل المصادفة أنني حددت بالملل: "... إذا كنت تأخذ نقطة الوسط الهندسية لكائن .." ، من المفهوم هنا أن نقاط الظل تكمن في خط مستقيم معين يشكّل محور الدوران الذي يمر عبر مركز ثقل الكائن. في هذه الحالة ، في الواقع ، سيكون الموضع المستقر هو الوضع الذي يكون فيه مركز الثقل أسفل المحور. ولكن إذا كان محور الدوران الذي تشكلته الأصابع يمر عبر مركز الثقل ، فسيكون النظام في حالة توازن غير مبال - لن يهتم بكيفية توجيهه.

ما الذي يجعل ريشة ذات وزن صغير ، أو قنبلة من الجوز ، أو بالون بالونات في سلة تجعلك تتنقل بالطريقة "الصحيحة"؟ الهواء. انه "يحمل" أجسامنا بحيث المحور يمر فوق مركز الثقل. بتعبير أدق ، مجرى هواء قادم يخلق قوة موزعة على منطقة الجسم. وستقع نقطة تطبيق الشرطية لهذه القوة بالقرب من المركز الهندسي لمربع الشكل. لجعله أكثر وضوحًا ، سنرسم القوى المؤثرة على البالون الشرطي ، كما هو الحال في كائن ذي كثافة غير متساوية:

القوى التي تجلب البالون في وضع مستقر.

ماذا عن شطيرة؟

أولاً ، إذا "أوقفنا" الهواء ، فسوف يسقط ببساطة. في السقوط الحر ، يدور الجسم حول مركز الكتلة بدقة ، بحيث لا يكون لديه سبب للانقلاب بأي طريقة خاصة. كما يقولون في المدرسة: "في المصعد المتساقط ، لوحظ انعدام الوزن". الزبدة في ساندويتش هو نفسه لا وزن له.

يمكن أن يؤثر الزيت الكثيف على عملية الانزلاق ، فإنه سيرفع بفعالية مركز الكتلة فوق اللمسة الدقيقة وتغيير في التعبير عن التسارع الزاوي $$$ل$ على $$$\ sqrt {l ^ 2 + d ^ 2} = l \ sqrt {1+ \ delta ^ 2}$ اين $$$\ دلتا = د / ل$ - السماكة النسبية للشطيرة. لقيم صغيرة $$$\ دلتا$ هذا التعبير يمكن حسابها $$$l (1+ \ delta ^ 2/2)$ . نحصل ، كما يقولون ، على تأثير من الدرجة الثانية. لشطيرة مع نسبة العرض إلى سمك كما $$ ل $$$1$ ، التغييرات النسبية لا تتجاوز $$$2 \٪$ . وهذا هو الحد الأقصى الأقصى للتأثير ، لأننا رفعنا مركز الكتلة إلى سمك الشطيرة ، التي تتوافق مع زيت كثيف بشكل لا نهائي!

الآن نقوم بإعادة تشغيل الهواء ، وترك كثافة الزيت أعلى بشكل غير محدود من كثافة الخبز. لدينا صفيحة كثيفة رقيقة مع مظلة خفيفة الوزن ولكنها مقاومة للهواء. في حين أن طائرة الساندويتش أفقية أو نحو ذلك ، فإن لحظة مقاومة الهواء تتناسب مع الرياح التي تعمل عليها - المنطقة التي يتفاعل معها تدفق الهواء: $$$M _ {-} \ propto l ^ 2$ . في الوضع المستقيم ، ستنخفض سرعة الرياح وبالتالي ستكون اللحظة مختلفة: $$$M_ {|} \ propto l d$ . نسبة هذه النقاط: $$$M_ {|} / M _ {-} \ propto \ delta.$ لقد كتبت علامة تناسبية هنا ، لأن معاملات المقاومة للوحة الموجودة على طول التدفق وعلى طوله مختلفة ، وهي غير معروفة بالنسبة لي. ولكن ليست هناك حاجة - من الواضح بالفعل أن تأثير الهواء في الوضع الرأسي (أي أنه يجعل وضع الزيت غير متساوٍ) أضعف من وضعه الأفقي. والآن نذكر أن الساندويتش تدور ، مما يعني أنه يتم استبداله بالتدفق إما بنهاية أو بالطائرة. يمكننا تقديم مقياس لعمل قوى المقاومة. إذا لم تتغير السرعة الزاوية للتناوب بشكل كبير في فترة واحدة (وهذا هو الحال بالنسبة للهواء) ، فمن المنطقي أن نتخذ كتدبير التغير في الزخم الزاوي الذي يتناسب مع مدة القوة. في المقابل ، فإن فترة العمل تتناسب مع زاوية "اجتاحت" من قبل شطيرة خلال هذه الفترة. نتيجة لذلك ، تدابير لحظات العمل $$$M_ {|}$ و $$$M _ {-}$ سوف تكون متناسبة $$$M_ {|} \ varphi_ {|}$ و $$$M _ {-} \ varphi _ {-}$ حيث يتم عرض الزوايا التي تجتاح النهاية والمستوى في الرسم. 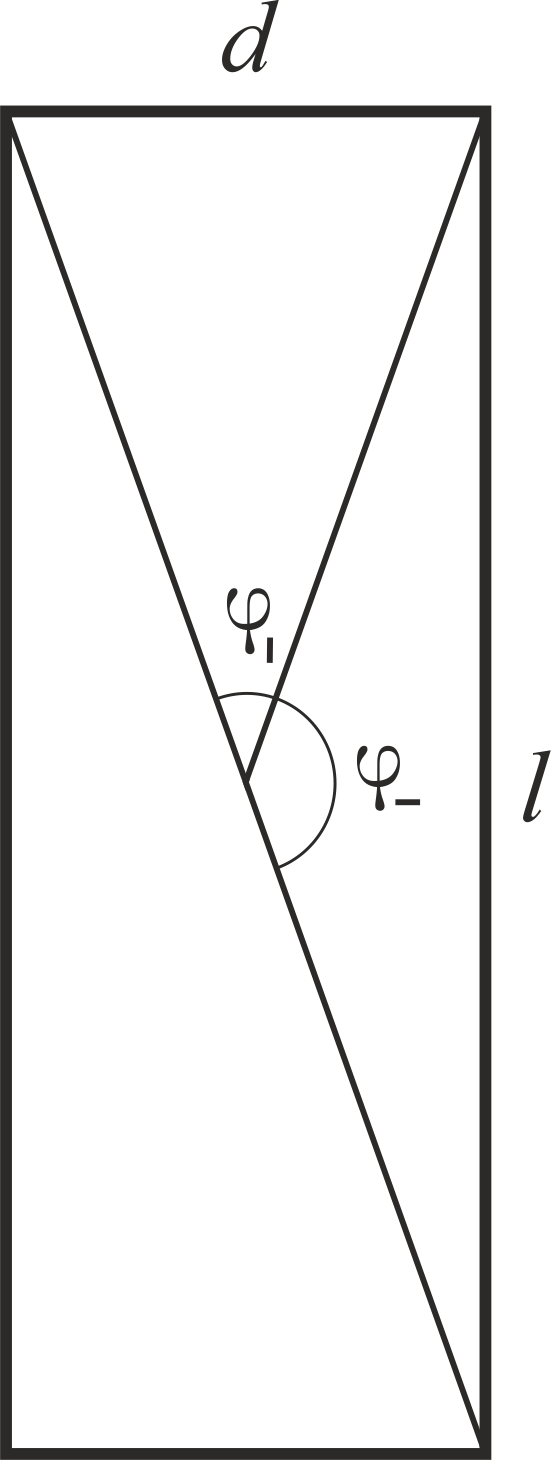يمكننا استخدام عمل قوى المقاومة كتدبير والحصول على نفس النسبة. نسبة الزاوية سهلة لحساب:

$$

$$\ frac {\ varphi_ {|}} {\ varphi _ {-}} = \ frac {\ varphi_ {|}} {\ frac {\ pi} {2} - \ varphi_ {|}}.$$

في الصغيرة $$$د / ل$ ، $$$\ varphi_ {|} \ sim \ delta$ (نستخدم خاصية الظل من زاوية صغيرة $$$10 \٪$ دقة في زوايا أقل $$$30 ^ \ circ$ ) ، وبالتالي ، لدينا:

$$

$$\ frac {M_ {|} \ varphi_ {|}} {M _ {-} \ varphi _ {-}} \ sim \ delta \ frac {\ delta} {\ frac {\ pi} {2} - \ delta} \ propto \ delta ^ 2.$$

مرة أخرى ، اتضح أن تأثير عدم التماثل لسندويتش مسطح محدود بتأثير الدرجة الثانية. عادةً ما تكون كثافة الزبدة ضعف كثافة الزبدة فقط ، ولا يتجاوز مركز الإزاحة الجماعية ثلث سمك السندويتش بطبقة معقولة من الزبدة لا تتجاوز سمك الخبز. هذه الملاحظة سوف تقلل من تأثير الزيت على $$ .

إذا بدا للقارئ أننا نطلق النار الآن على العصافير من البندقية ، فأنا أتفق معه تمامًا. لكن ، أولاً ، لا أريد أن أسمع المزيد عن النفط "المتفوق" ، وثانياً ، لا أريد أن أكون بلا أساس ، وثالثًا ، أردت أن أوضح كيف يقدر الفيزيائي الكميات ، ويمثل العملية ، ولكن لا يمتلك بيانات كاملة. بطبيعة الحال ، في وقت الهبوط ، يمكن للزبد التمسك بالأرض ومنع الساندويتش من القفز والانقلاب مرة أخرى ، لكنني بالتأكيد لن أفكك آليات التأثير والتشوه المرن والقفز بقطعة من الخبز. لذلك جاء الكثير من التحليل لهذه المشكلة. والثانية Shnobelevskaya لها لن تعطى.

$$

$$* * *$$

لم يكن هدف طريقنا في غاية الأهمية: دحض أو تبرير قانون السندوتش ، كالمسار نفسه. لقد أوضح كيف يتيح لك الجمع بين الطرق الرياضية المختلفة النظر إلى المشكلة من زوايا مختلفة ويوفر معرفة دقيقة إلى حد ما ، حتى بدون حل مفصل للمشكلة. اتساق مختلف التخصصات الرياضية ، والمقاربات ووجهات النظر هي قوة وجمال الرياضيات. من المناسب أن نتذكر الكلمات الرائعة لمارينا تسفيتيفا: "لا أريد أن يكون لدي وجهة نظر ، أريد أن أكون بصرًا" . يمكن أن تتيح دراسة مجالات الرياضيات المختلفة للباحث رؤية "متعددة الحجمي" حقيقية متعددة الأبعاد ، والتي تسمح لك بالنظر إلى مساحة المعرفة المغلقة والمختفية على ما يبدو.