ربما ، فإن أي خدمة ذات بحث عام ، تأتي عاجلاً أم آجلاً في معرفة كيفية إصلاح الأخطاء في استعلامات المستخدم. Errare humanum est؛ يتم غلق المستخدمين وخطئهم باستمرار ، ونوعية البحث لا محالة في ذلك - ومعها تجربة المستخدم.

علاوة على ذلك ، لكل خدمة تفاصيلها الخاصة ، والمفردات الخاصة بها ، والتي ينبغي أن تكون قادرة على تشغيل مصحح الأخطاء المطبعية ، مما يعقد إلى حد كبير استخدام الحلول الحالية. على سبيل المثال ، يجب أن تتعلم مثل هذه الطلبات تحرير الوصي لدينا:



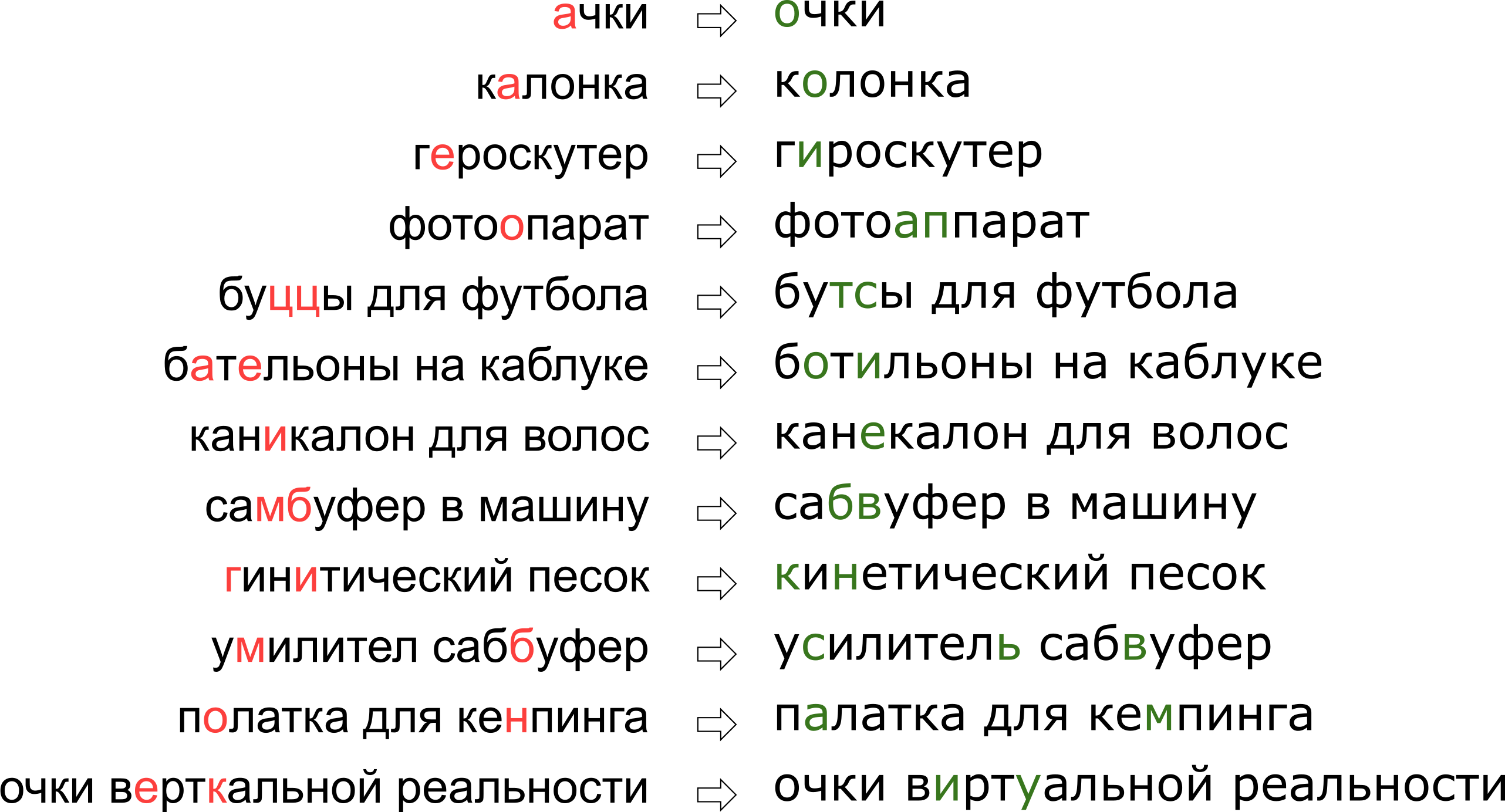قد يبدو أننا أنكرنا للمستخدم حلمه الواقعي العمودي ، ولكن في الحقيقة الحرف K يقف ببساطة على لوحة المفاتيح بجانب الحرف U.

في هذه المقالة ، سننظر في أحد الأساليب التقليدية لتصحيح الأخطاء المطبعية ، من بناء نموذج إلى كتابة التعليمات البرمجية في Python and Go. وكمكافأة - فيديو من تقريري " نظارات الواقع عموديًا": نقوم بتصحيح الأخطاء المطبعية في استعلامات البحث على Highload ++.

بيان المشكلة

لذلك ، تلقينا طلبًا مختومًا ونحتاج إلى إصلاحه. عادة ، يتم طرح المشكلة رياضيا على النحو التالي:

• أعطيت الكلمة $$$s$ تنتقل إلينا مع الأخطاء.
• لديك قاموس $$$\ سيجما$ الكلمات الصحيحة
• لجميع الكلمات ث في القاموس هناك احتمالات مشروطة $$$P (w | s)$ ماذا كان المقصود بالكلمة $$$w$ شريطة أن حصلنا على الكلمة $$$s$ ؛
• تحتاج إلى العثور على الكلمة w من القاموس مع أقصى الاحتمالات $$$P (w | s)$ .

يشير هذا البيان - الأكثر أهمية - إلى أننا إذا تلقينا طلبًا من عدة كلمات ، فسوف نقوم بتصحيح كل كلمة على حدة. في الواقع ، بالطبع ، سوف نريد تصحيح العبارة بأكملها ككل ، بالنظر إلى توافق الكلمات المجاورة ؛ سأتحدث عن هذا لاحقًا في قسم "كيفية تصحيح العبارات".

هناك لحظات غير واضحة - للحصول على القاموس وكيفية حسابه $$$P (w | s)$ . السؤال الأول يعتبر بسيط. في عام 1990 [1] ، تم تجميع القاموس من قاعدة بيانات أداة الإملاء وقواميس متوفرة إلكترونيًا ؛ في عام 2009 ، كان Google [4] أكثر بساطة وأخذ الكلمات الأكثر شيوعًا على الإنترنت (مع الأخطاء الإملائية الشائعة). أخذت هذا النهج لبناء الوصي بلدي.

السؤال الثاني أكثر تعقيدًا. إذا فقط لأن قراره يبدأ عادة بتطبيق صيغة بايز!

$$

$$P (w | s) = \ mathrm {const} \ cdot P (s | w) \ cdot P (w)$$

الآن ، بدلاً من الاحتمال الأولي غير المفهوم ، نحتاج إلى تقييم نوعين جديدين أكثر قابلية للفهم: $$$P (s | w)$ - احتمال أنه عند كتابة كلمة $$$w$ يمكن أن تكون مختومة والحصول عليها $$$s$ و $$$P (w)$ - من حيث المبدأ ، احتمال المستخدم باستخدام الكلمة $$$w$ .

كيف تقيم $$$P (s | w)$ ؟ من الواضح أن المستخدم من المرجح أن يخلط بين A و O أكثر من b مع S. وإذا صححنا النص الذي تم التعرف عليه من المستند الممسوح ضوئيًا ، فهناك احتمال كبير للارتباك بين rn و m. بطريقة أو بأخرى ، نحتاج إلى نوع من النماذج التي تصف الأخطاء واحتمالاتها.

يُطلق على هذا النموذج نموذج القناة الصاخبة (نموذج القناة الصاخبة ؛ وفي حالتنا ، تبدأ القناة الصاخبة في مكان ما في وسط Brock للمستخدم وتنتهي على الجانب الآخر من لوحة المفاتيح الخاصة به) أو ، باختصار ، نموذج الخطأ هو نموذج الخطأ. هذا النموذج ، الذي تمت مناقشته في قسم منفصل أدناه ، سيكون مسؤولاً عن مراعاة كل من الأخطاء الإملائية ، وفي الواقع ، الأخطاء المطبعية.

معدل احتمال استخدام الكلمة - $$$P (w)$ - من الممكن بطرق مختلفة. أبسط خيار هو أخذ التردد الذي تحدث به الكلمة في مجموعة كبيرة من النصوص. بالنسبة إلى الوصي لدينا ، مع الأخذ في الاعتبار سياق العبارة ، بالطبع ، هناك حاجة إلى شيء أكثر تعقيدًا - نموذج آخر. هذا النموذج يسمى نموذج اللغة ، نموذج اللغة.

نموذج خطأ

تم النظر في نماذج الخطأ الأولى $$$P (s | w)$ ، حساب احتمالات البدائل الأولية في مجموعة التدريب: كم مرة بدلاً من E كتبوا ، وكم مرة بدلاً من T كتبوا T ، بدلاً من T - T وهكذا [1]. كانت النتيجة نموذجًا يحتوي على عدد صغير من المعلمات التي يمكن أن تتعلم بعض التأثيرات المحلية (على سبيل المثال ، كثيرًا ما يخلط الناس بين E و I).

في بحثنا ، توصلنا إلى نموذج خطأ أكثر تطوراً اقترحه بريل ومور في عام 2000 [2] وأعيد استخدامه لاحقًا (على سبيل المثال ، من قِبل خبراء Google [4]). تخيل أن المستخدمين لا يفكرون في أحرف منفصلة (تخلط بين E و I ، اضغط K بدلاً من Y ، وتخطي علامة ناعمة) ، ولكن يمكنهم تغيير القطع التعسفية للكلمة إلى أي شخص آخر - على سبيل المثال ، استبدل TSYA بـ TYSYA ، Y بـ K ، SHA مع SHCHYA ، SS إلى C وهلم جرا. احتمال أن المستخدم مختوم وبدلاً من TSYA كتب THY ، نشير إلى ذلك $$$P (\ text {آلاف} \ rightarrow \ text {آلاف})$ هو معلمة من نموذجنا. إذا لجميع الشظايا الممكنة $$$\ alpha ، \ beta$ يمكننا الاعتماد $$$P (\ alpha \ rightarrow \ beta)$ ، ثم الاحتمال المطلوب $$$P (s | w)$ يمكن الحصول على مجموعة من الكلمة s عند محاولة كتابة الكلمة w في نموذج Brill و Moore على النحو التالي: نقوم بتقسيم الكلمات w و s إلى أجزاء أقصر بكل الطرق الممكنة حتى يكون هناك نفس عدد الأجزاء في كلمتين. لكل قسم ، نقوم بحساب منتج احتمالات جميع الأجزاء w ليتحول إلى الأجزاء المقابلة s. سيتم أخذ الحد الأقصى لجميع هذه الأقسام كقيمة $$$P (s | w)$ :

$$

$$P (s | w) = \ max_ {s = \ alpha_1 \ alpha_2 \ ldots \ alpha_k ، w = \ beta_1 \ beta_2 \ ldots \ beta_k} P (\ alpha_1 \ rightarrow \ beta_1) \ cdot P (\ alpha_2 \ rightarrow \ beta_2) \ cdot \ ldots \ cdot P (\ alpha_k \ rightarrow \ beta_k) \ ،.$$

دعونا نلقي نظرة على مثال للقسم الذي يحدث عند حساب احتمال طباعة "ملحق" بدلاً من "ملحق":

$$

$$\ تبدأ {matrix} \ text {ak} & \ text {cec} & \ text {sou} & \ text {a} & \ text {p} \\ \ downarrow & \ downarrow & \ downarrow & \ downarrow & \ downarrow \\ \ text {a} & \ text {cc} & \ text {e} & \ text {soua} & \ text {p} \ end {matrix}$$

كما لاحظت على الأرجح ، هذا مثال على قسم غير ناجح للغاية: من الواضح أن أجزاء من الكلمات لم تكمن تحت بعضها البعض بنجاح كما يمكن. إذا كانت الكميات $$$P (\ text {ak} \ rightarrow \ text {a})$ و $$$P (\ text {p} \ rightarrow \ text {p})$ لا يزال ليس سيئا للغاية بعد ذلك $$$P (\ text {sou} \ rightarrow \ text {e})$ و $$$P (\ text {a} \ rightarrow \ text {soua})$ على الأرجح سوف يجعلون "النتيجة" النهائية لهذا القسم محزنة تمامًا. يبدو القسم الأكثر نجاحًا مثل هذا:

$$

$$\ تبدأ {matrix} \ text {ak} & \ text {ce} & \ text {ss} & \ text {y} & \ text {ar} \\ \ downarrow & \ downarrow & \ downarrow & \ downarrow & \ downarrow \\ \ text {ak} & \ text {ce} & \ text {c} & \ text {y} & \ text {ar} \ end {matrix}$$

هنا ، وقع كل شيء على الفور في مكانه ، ومن الواضح أن الاحتمال النهائي سيتم تحديده في المقام الأول حسب القيمة $$$P (\ text {ss} \ rightarrow \ text {s})$ .

كيفية حساب $$$P (s | w)$

على الرغم من حقيقة أن هناك أوامر من أقسام محتملة لكلمتين $$$O (2 ^ {| s | + | w |})$ باستخدام خوارزمية حساب البرمجة الديناميكية $$$P (s | w)$ يمكن جعل سريع جدا ل $$$O (| s | ^ 2 | w | ^ 2)$ . تشبه الخوارزمية نفسها بقوة خوارزمية فاغنر فيشر لحساب مسافة ليفينشتاين .

سننشئ جدولًا مستطيلًا ، تتوافق صفوفه مع أحرف الكلمة الصحيحة ، والأعمدة مع العمود المختوم. سيكون للخلية عند تقاطع الصف i والعمود j بنهاية الخوارزمية احتمال الحصول على s[:j] عند محاولة طباعة w[:i] . من أجل حسابها ، يكفي حساب قيم جميع الخلايا في الصفوف والأعمدة السابقة وتجاوزها ، مضروبة في المقابل $$$P (\ alpha \ rightarrow \ beta)$ . على سبيل المثال ، إذا كان لدينا جدول شغل


، ثم لملء الخلية في الصف الرابع والعمود الثالث (الرمادي) يجب أن تأخذ الحد الأقصى $$$0.8 \ cdot P (\ text {cc} \ rightarrow \ text {c})$ و $$$0.16 \ cdot P (\ text {c} \ rightarrow \ text {k})$ . في الوقت نفسه ، مررنا بجميع الخلايا المظللة في الصورة باللون الأخضر. إذا نظرنا أيضًا في تعديلات النموذج $$$P (\ alpha \ rightarrow \ text {blank line})$ و $$$P (\ text {سطر فارغ} \ rightarrow \ beta)$ ، ثم عليك أن تذهب فوق الخلايا المظللة باللون الأصفر.

تعقيد هذه الخوارزمية ، كما ذكرت أعلاه ، هو $$$O (| s | ^ 2 | w | ^ 2)$ : نحن ملء الجدول $$$| s | \ times | w |$ ولملء الخلية (i ، j) التي تحتاجها $$$O (i \ cdot j)$ العمليات. ومع ذلك ، إذا قصرنا نظرتنا على أجزاء لا تزيد عن بعض الطول المحدود $$$L$ (على سبيل المثال ، لا يزيد عن حرفين ، كما في [4]) ، سينخفض ​​التعقيد إلى $$$O (| s | \ cdot | w | \ cdot L ^ 2)$ . للغة الروسية في تجاربي التي أجريتها $$$L = 3 دولا$ .

كيفية تعظيم $$$P (s | w)$

علمنا أن نجد $$$P (s | w)$ لوقت كثير الحدود هو جيد. لكننا بحاجة لمعرفة كيفية العثور بسرعة على أفضل الكلمات في القاموس بأكمله. والأفضل ليس كذلك $$$P (s | w)$ لكن $$$P (w | s)$ ! في الواقع ، يكفي أن نحصل على بعض الكلمات المعقولة (على سبيل المثال ، أفضل 20 كلمة) $$$P (s | w)$ ، والتي سنرسلها بعد ذلك إلى نموذج اللغة لتحديد التصحيحات الأكثر ملاءمة (المزيد حول هذا أدناه).

لمعرفة كيفية الانتقال السريع إلى القاموس بأكمله ، نلاحظ أن الجدول الموضح أعلاه سيكون له الكثير من القواسم المشتركة لكلمتين لهما بادئات مشتركة. في الواقع ، إذا صححنا كلمة "ملحق" ، وحاولنا تعبئتها للكلمتين المفردتين "ملحق" و "ملحق" ، فسوف نلاحظ أن الأسطر التسعة الأولى فيها لا تختلف على الإطلاق! إذا استطعنا ترتيب عملية تمرير قاموس بحيث تكون للكلمتين التاليتين بادئات مشتركة طويلة بما فيه الكفاية ، فيمكننا حفظ الكثير من العمليات الحسابية.

ونحن نستطيع. دعونا نأخذ الكلمات المفردات وجعلها trie . عند المرور بعمق ، نحصل على الخاصية المطلوبة: معظم الخطوات هي خطوات من العقدة إلى سلالتها ، عندما يحتاج الجدول إلى ملء الصفوف القليلة الأخيرة.

تتيح لنا هذه الخوارزمية ، مع بعض التحسينات الإضافية ، فرز قاموس بلغة أوروبية نموذجية من 50 إلى 100 ألف كلمة في حدود مائة مللي ثانية [2]. التخزين المؤقت للنتائج سيجعل العملية أسرع.

كيف تحصل عليه $$$P (\ alpha \ rightarrow \ beta)$

حساب $$$P (\ alpha \ rightarrow \ beta)$ لجميع الشظايا قيد النظر - الجزء الأكثر إثارة للاهتمام وغير تافهة من بناء نموذج خطأ. من هذه الكميات التي ستعتمد جودتها.

النهج المستخدم في [2 ، 4] بسيط نسبيا. دعنا نجد الكثير من الأزواج $$$(s_i ، w_i)$ اين $$$w_i$ هي الكلمة الصحيحة من القاموس ، و $$$s_i$ - نسخته مختومة. (كيف بالضبط العثور عليها أقل قليلاً.) الآن نحن بحاجة إلى استخراج احتمالات الأخطاء المطبعية محددة من هذه الأزواج (استبدال بعض شظايا مع الآخرين).

لكل زوج نأخذ مكوناته $$$w$ و $$$s$ وبناء المراسلات بين رسائلهم ، مما يقلل من المسافة Levenshtein:

$$

$$\ تبدأ {matrix} \ text {a} & \ text {c} & \ text {c} & \ text {e} & \ text {c} & \ text {c} & \ text {y} & \ text {a} & \ text {p} \\ \ text {a} & \ text {k} & \ text {c} & \ text {e} & \ text {c} & \ text {} & \ text {y } & \ text {a} & \ text {p} \ end {matrix}$$

الآن نرى على الفور البدائل: a a و a و e و c و c و c و a سلسلة فارغة وهكذا. نرى أيضًا بدائل مكونة من حرفين أو أكثر: ak → ak، ce → si، ec → is، ss → s، ses → sis، ess → is and other ، وهكذا. يجب حساب كل هذه البدائل ، وفي كل مرة تحدث فيها الكلمة s في الجسم (إذا أخذنا الكلمات من الجسم ، وهو أمر محتمل جدًا).

بعد المرور في جميع الأزواج $$$(s_i ، w_i)$ لاحتمال $$$P (\ alpha \ rightarrow \ beta)$ يتم قبول عدد البدائل α → β التي حدثت في أزواجنا (مع الأخذ في الاعتبار حدوث الكلمات المقابلة) مقسومًا على عدد مرات تكرار الجزء α.

كيف تجد الأزواج $$$(s_i ، w_i)$ ؟ في [4] ، تم اقتراح هذا النهج. خذ المحتوى الكبير من المحتوى الذي أنشأه المستخدمون (UGC). في حالة Google ، كان مجرد نصوص لمئات الملايين من صفحات الويب ؛ لدينا الملايين من عمليات البحث والاستعراض المستخدم. من المفترض أنه عادةً ما توجد الكلمة الصحيحة في الجسم في كثير من الأحيان أكثر من أي من المتغيرات الخاطئة. لذلك ، دعونا نجد كلمات لكل كلمة قريبة منها من Levenshtein من مجموعة ، والتي هي أقل شعبية بكثير (على سبيل المثال ، عشر مرات). خذ شعبية $$$w$ ، أقل شعبية - ل $$$s$ . لذلك نحن نحصل على صاخبة ، ولكن مجموعة كبيرة من الأزواج التي يتدرب عليها.

هذه الخوارزمية المطابقة للزوج تترك مجالًا كبيرًا للتحسين. في [4] ، مرشح فقط عن طريق الحدوث ( $$$w$ عشر مرات أكثر شعبية من $$$s$ ) ، لكن مؤلفي هذه المقالة يحاولون تكوين ثرثرة ، دون استخدام أي معرفة مسبقة باللغة. إذا أخذنا في الاعتبار اللغة الروسية فقط ، فيمكننا ، على سبيل المثال ، أن نأخذ مجموعة من قواميس أشكال الكلمات الروسية وأن نترك أزواج فقط مع الكلمة $$$w$ وجدت في القاموس (ليست فكرة جيدة ، لأن القاموس لن يحتوي على الأرجح على مفردات خاصة بالخدمة) أو ، على العكس من ذلك ، تجاهل أزواج مع الكلمة s الموجودة في القاموس (أي ، يكاد يكون مضمونًا عدم الإغلاق).

لتحسين جودة الأزواج المستلمة ، كتبت وظيفة بسيطة تحدد ما إذا كان المستخدمون يستخدمون كلمتين كمرادفات. المنطق بسيط: إذا وجدت الكلمات w و s محاطة بالكلمات نفسها ، فربما تكون مرادفات - والتي ، في ضوء قربها وفقًا Levenshtein ، تعني أن الكلمة الأقل شيوعًا هي على الأرجح نسخة خاطئة من كلمة أكثر شعبية. بالنسبة لهذه العمليات الحسابية ، استخدمت إحصائيات الحدوث الثلاثي (عبارات من ثلاث كلمات) المصممة لنموذج اللغة أدناه.

نموذج اللغة

لذلك ، الآن لكلمة قاموس معينة ث ، نحتاج إلى حساب $$$P (w)$ - احتمال استخدامه من قبل المستخدم. إن أبسط الحلول هو أخذ كلمة في حالة كبيرة. بشكل عام ، على الأرجح ، يبدأ أي نموذج لغوي بجمع مجموعة كبيرة من النصوص وحساب حدوث الكلمات فيه. لكن لا ينبغي لنا أن نقتصر على ذلك: في الواقع ، عند حساب P (w) ، يمكننا أيضًا أن نأخذ بعين الاعتبار العبارة التي نحاول تصحيح الكلمة بها ، وأي سياق خارجي آخر. المهمة تتحول إلى مهمة حسابية $$$P (w_1w_2 \ ldots w_k)$ حيث واحد من $$$w_i$ - الكلمة التي قمنا بتصحيح الخطأ المطبعي والتي نحسبها الآن $$$P (w)$ والباقي $$$w_i$ - الكلمات المحيطة بالكلمة المصححة في طلب المستخدم.

لمعرفة كيفية أخذها في الحسبان ، يجدر بك أن تمر من خلال المجموعة مرة أخرى وتجميع إحصائيات n-gram وتسلسل الكلمات. عادة ما تأخذ تسلسلات ذات طول محدود. لقد حصرتُ نفسي في البرامج ثلاثية الأبعاد حتى لا أضخِّم الفهرس ، لكن كل هذا يتوقف على قوتك الذهنية (وحجم الحالة - على حالة صغيرة ، حتى الإحصائيات حول أشكال ثلاثية الأبعاد ستكون صاخبة للغاية).

نموذج اللغة التقليدية ن غرام يشبه هذا. لهذه العبارة $$$w_1w_2 \ ldots w_k$ يتم احتساب احتماله بواسطة الصيغة

$$

$$P (w_1w_2 \ ldots w_k) = P (w_1) \ cdot P (w_2 | w_1) \ cdot P (w_3 | w_1w_2) P (w_k | w_1w_2w_ {k-1}) \ ،$$

اين $$$P (w_1)$ - مباشرة وتيرة الكلمة ، و $$$P (w_3 | w_1w_2)$ - احتمال الكلمة $$$w_3 دولا$ شريطة أن قبل أن يذهب $$$w_1w_2$ - لا شيء سوى نسبة تردد trigram $$$w_1 w_2 w_3$ لتردد بيغرام $$$w_1 w_2$ . (لاحظ أن هذه الصيغة هي ببساطة نتيجة الاستخدام المتكرر لصيغة بايز.)

وبعبارة أخرى ، إذا كنا نريد حساب $$$P (\ text {mom soap frame})$ ، تدل على وتيرة التعسفي ن غرام في $$$و$ نحصل على الصيغة

$$

$$P (\ text {mom soap frame}) = f (\ text {mom}) \ cdot \ frac {f (\ text {mom soap})} {f (\ text {mom})} \ cdot \ frac { f (\ text {mom soap frame})} {f (\ text {mom soap})} = f (\ text {mom soap frame}) \،.$$

هل هو منطقي؟ هو منطقي. ومع ذلك ، تبدأ الصعوبات عندما تصبح العبارات أطول. ماذا لو قام المستخدم بإدخال استعلام بحث مكون من عشر كلمات بتفاصيل رائعة؟ لا نريد الاحتفاظ بالإحصائيات لكل 10 غرامات - هذا مكلف ، ومن المحتمل أن تكون البيانات صاخبة وليست إرشادية. نحن نريد أن ننتقل من خلال n-gram ذات طول محدود - على سبيل المثال ، الطول 3 المقترح بالفعل أعلاه.

هذا هو المكان الذي تأتي فيه الصيغة أعلاه في متناول اليدين. لنفترض أن احتمال ظهور كلمة ما في نهاية عبارة ما يتأثر بشكل كبير فقط ببضع كلمات أمامها مباشرةً ، أي

$$

$$P (w_k | w_1w_2 \ ldots w_ {k-1}) \ approx P (w_k | w_ {k-L + 1} \ ldots w_ {k-1}) \،.$$

وضع $$$L = 3 دولا$ ، لفترة أطول نحصل على الصيغة


$$$P (\ text {carl stoll coral from Clara}) \ approx f (\ text {carl}) \ cdot \ frac {f (\ text {carl})} {f (\ text {carl})} \ cdot \ frac {f (\ text {carl from clara})} {f (\ text {carl from})} \ cdot \ frac {f (\ text {stole from clara})} {f (\ text {from clara} )} \ cdot \ frac {f (\ text {claire stole coral})} {f (\ text {claire stole})} \،.$


يرجى ملاحظة: تتكون العبارة من خمس كلمات ، ولكن n غرام لا تزيد عن ثلاث تظهر في الصيغة. هذا هو بالضبط ما سعينا إليه.

كان هناك لحظة رقيقة واحدة اليسار. ماذا لو قام المستخدم بإدخال عبارة غريبة جدا و n غرام المقابلة في إحصاءاتنا وليس على الإطلاق؟ سيكون من السهل وضع غرامات غير مألوفة $$$f = 0$ إذا لم يكن من الضروري القسمة على هذه القيمة. هنا يأتي للمساعدة في تجانس (تجانس) ، والذي يمكن القيام به بطرق مختلفة ؛ ومع ذلك ، فإن المناقشة التفصيلية للنُهج الجادة المضادة للتعرج ، مثل تجانس Kneser-Ney ، تتجاوز بكثير نطاق هذه المقالة.

كيفية تصحيح العبارات

نناقش آخر نقطة خفية قبل الانتقال إلى التنفيذ. يتضمن بيان المشكلة التي وصفتها أعلاه وجود كلمة واحدة ويجب إصلاحها. ثم أوضحنا أن هذه الكلمة قد تكون في منتصف عبارة من بين بعض الكلمات الأخرى ، ويجب أيضًا أخذها في الاعتبار ، واختيار أفضل تصحيح. ولكن في الواقع ، يقوم المستخدمون ببساطة بإرسال عبارات إلينا دون تحديد الكلمة التي يتم تهجئتها ؛ في كثير من الأحيان بضع كلمات أو حتى جميع تحتاج إلى تصحيح.

يمكن أن يكون هناك العديد من النهج. على سبيل المثال ، يمكنك أن تأخذ في الاعتبار فقط السياق الأيسر للكلمة في العبارة. ثم ، وفقًا للكلمات من اليسار إلى اليمين وتصحيحها حسب الضرورة ، سوف نحصل على عبارة جديدة ذات جودة. ستكون الجودة رديئة إذا تحولت الكلمة الأولى ، على سبيل المثال ، إلى عدة كلمات شائعة واخترنا الخيار غير الصحيح. سيتم ضبط العبارة المتبقية بأكملها (ربما في البداية خالية تمامًا من الأخطاء) بواسطة الكلمة الأولى الخاطئة ويمكننا الحصول على النص الذي لا صلة له بالأصل تمامًا.

يمكنك النظر في الكلمات بشكل فردي وتطبيق مصنف معين لفهم ما إذا كانت الكلمة المقدمة مختومة أم لا ، كما هو مقترح في [4]. يتم تدريب المصنف على الاحتمالات التي نعرفها بالفعل كيف نحسب ، وعدد من الميزات الأخرى. إذا ذكر المصنف ما الذي يجب إصلاحه ، فإننا نقوم بتصحيحه ، بالنظر إلى السياق الحالي. مرة أخرى ، إذا تم تهجئة العديد من الكلمات بشكل غير صحيح ، فسيتعين عليك اتخاذ قرار بشأن أولها بناءً على السياق الذي يحتوي على الأخطاء ، مما قد يؤدي إلى مشاكل في الجودة.

في تنفيذ الوصي لدينا ، استخدمنا هذا النهج. دعنا لكل كلمة $$$s_i$ في عبارة لدينا ، باستخدام نموذج الخطأ ، نجد كلمات قاموس top-N التي يمكن أن تعني ، نجمعها في عبارات بكل طريقة ممكنة ولكل من $$$N ^ K$ العبارات الناتجة حيث $$$K$ - عدد الكلمات في العبارة الأصلية ، بحساب القيمة بصدق

$$

$$P (s_1 | w_1) \ cdot P (s_K | w_K) \ cdot P (s_K | w_K) \ cdot P (w_1w_2 \ ldots w_K) ^ {\ lambda} \،.$$

هنا $$$s_i$ - الكلمات التي أدخلها المستخدم ، $$$w_i$ - تصحيحات مختارة لهم (والتي نقوم الآن بالفرز منها) ، و $$$\ lambda$ - معامل يحدده النوعية النسبية لنموذج الخطأ ونموذج اللغة (معامل كبير - نحن نثق في نموذج اللغة أكثر ، معامل صغير - نحن نثق في نموذج الخطأ أكثر) ، المقترح في [4]. في المجموع ، بالنسبة لكل عبارة ، نقوم بضرب احتمالات الكلمات الفردية التي يجب تصحيحها في المتغيرات المقابلة للقاموس ، ونضربها أيضًا باحتمال العبارة بأكملها في لغتنا. نتيجة الخوارزمية عبارة من كلمات القاموس التي تزيد هذه القيمة.

لذا توقف ماذا؟ القوة الغاشمة $$$N ^ K$ عبارات؟

لحسن الحظ ، نظرًا لحقيقة أننا حددنا طول n-grams ، فمن الممكن العثور على الحد الأقصى في جميع العبارات بشكل أسرع بكثير. تذكر: أعلاه نحن تبسيط صيغة ل $$$P (w_1w_2 \ ldots w_K)$ بحيث بدأت تعتمد فقط على ترددات n غرام لا يزيد طولها عن ثلاثة:

$$

$$P (w_1w_2 \ ldots w_K) = P (w_1) \ cdot P (w_2 | w_1) \ cdot P (w_3 | w_1w_2) \ cdot \ ldots \ cdot P (w_K | w_ {K-2} w_ {K-1 }) \ ،.$$

إذا ضربنا هذه القيمة بـ $$$P (s_i | w_i)$ ومحاولة تعظيم $$$w_K$ ، سنرى أنه يكفي فرز جميع أنواع $$$w_ {K-2}$ و $$$w_ {K-1}$ وحل المشكلة بالنسبة لهم - وهذا هو ، عن العبارات $$$w_1w_2 \ ldots w_ {K-2} w_ {K-1}$ . في المجموع ، يتم حل المشكلة عن طريق البرمجة الديناميكية في $$$O (KN ^ 3)$ .

التنفيذ

وضع القضية معًا وعدّ عدد الجرام

سأقوم بالحجز على الفور: لم يكن هناك الكثير من البيانات تحت تصرفي لبدء بعض MapReduce المعقدة. لذلك جمعت للتو جميع نصوص المراجعات والتعليقات واستفسارات البحث باللغة الروسية (أوصاف السلع ، للأسف ، تأتي باللغة الإنجليزية ، واستخدام نتائج الترجمة التلقائية ساءت بدلاً من تحسين النتائج) من خدمتنا في ملف نصي واحد وتعيين الخادم على حساب الليلة ثلاثة أضعاف مع برنامج نصي بيثون بسيط.

كقاموس ، أخذت الكلمات العليا بشكل متكرر حتى أحصل على حوالي مائة ألف كلمة. تم استبعاد الكلمات الطويلة جدًا (أكثر من 20 حرفًا) والقصيرة جدًا (أقل من ثلاثة أحرف ، باستثناء الكلمات الروسية المشهورة والمشفقة). تم تجنيب الكلمات بشكل منفصل عن الانتظام r"^[a-z0-9]{2}$" - حتى نجحت إصدارات أجهزة iPhone وغيرها من المعرّفات المهمة بطول 2.

عند حساب الكلمات الكبيرة والثلاثية في عبارة ، قد تحدث كلمة غير قاموس. في هذه الحالة ، رميت هذه الكلمة وتغلبت على العبارة بأكملها في جزأين (قبل وبعد هذه الكلمة) ، والتي عملت بها بشكل منفصل. لذلك ، عن عبارة " هل تعرف ما هو" abyrvalg "؟ هذا هو ... HEADMAN ، زميل "سوف يأخذ في الاعتبار البرامج ثلاثية الأبعاد " هل تعلم "،" أنت تعرف ماذا ، "تعرف ما هو" و "هذا هو زميل صياد السمك الرئيسي" (ما لم ، بالطبع ، كلمة "headman" تدخل في القاموس ...).

نحن ندرب نموذج الخطأ

كذلك نفذت جميع عمليات معالجة البيانات في Jupyter. يتم تحميل الإحصائيات على n-grams من JSON ، ويتم إجراء مرحلة ما بعد المعالجة للعثور بسرعة على الكلمات القريبة من بعضها البعض وفقًا لـ Levenshtein ، وبالنسبة للأزواج في الحلقة ، يتم استدعاء دالة (مرهقة إلى حد ما) لترتيب الكلمات واستخراج التعديلات القصيرة للنموذج ss → c (تحت المفسد).


يبدو أن حساب التعديلات نفسها أساسي ، رغم أنه قد يستغرق وقتًا طويلاً.

تطبيق نموذج الخطأ

يتم تنفيذ هذا الجزء كخدمة صغرى على Go ، متصلة بالواجهة الخلفية الرئيسية عبر gRPC. تم تنفيذ الخوارزمية التي وصفها بريل ومور أنفسهم [2] ، مع تحسينات طفيفة. كنتيجة لي ، كنت بطيئًا كما ادعى المؤلفون ؛ لا أفترض أن أحكم على ما إذا كان موجودًا أم لا. لكن أثناء التنميط ، تعلمت بعض الشيء عن Go.

• لا تستخدم math.Max لحساب الحد الأقصى. هذا هو حوالي ثلاث مرات أبطأ مما if a > b { b = a } ! مجرد إلقاء نظرة على تنفيذ هذه الوظيفة :
  

   // Max returns the larger of x or y. // // Special cases are: // Max(x, +Inf) = Max(+Inf, x) = +Inf // Max(x, NaN) = Max(NaN, x) = NaN // Max(+0, ±0) = Max(±0, +0) = +0 // Max(-0, -0) = -0 func Max(x, y float64) float64 func max(x, y float64) float64 { // special cases switch { case IsInf(x, 1) || IsInf(y, 1): return Inf(1) case IsNaN(x) || IsNaN(y): return NaN() case x == 0 && x == y: if Signbit(x) { return y } return x } if x > y { return x } return y } 

  
  لا تستخدم math.Max إلا إذا كنت بحاجة إلى أن تكون +0 بالضرورة أكبر من -0.
  
• لا تستخدم جدول التجزئة إذا كان يمكنك استخدام صفيف. هذا ، بطبيعة الحال ، هو نصيحة واضحة جدا. اضطررت إلى إعادة ترقيم أحرف Unicode إلى أرقام في بداية البرنامج لاستخدامها كمؤشرات في صف أحفاد عقدة trie (مثل هذا البحث كان عملية شائعة جدًا).
  
• ردود الفعل في الذهاب ليست رخيصة. أثناء إعادة التجهيز خلال مراجعة التعليمات البرمجية ، تباطأت بعض محاولاتي لجعل الفصل بشكل كبير على الرغم من أن الخوارزمية لم تتغير رسميًا. منذ ذلك الحين ، كنت أرى أن برنامج التحويل البرمجي "تحسين الأداء" لديه مجال للنمو.
  

تطبيق نموذج اللغة

هنا ، دون أي مفاجآت ، تم تنفيذ خوارزمية البرمجة الديناميكية الموضحة في القسم أعلاه. كان هذا المكون أقل عمل - الجزء الأبطأ هو تطبيق نموذج الخطأ. لذلك ، بين هاتين الطبقتين ، تم تخزين التخزين المؤقت لنموذج الخطأ في Redis بالإضافة إلى ذلك.

النتائج

استنادًا إلى نتائج هذا العمل (الذي استغرق حوالي شهر) ، قمنا بإجراء اختبار اختبار A / B على مستخدمينا. بدلاً من 10٪ من نتائج البحث الفارغة بين جميع طلبات البحث التي كانت لدينا قبل إدخال الوصي ، كان هناك 5٪ منها ؛ في الأساس ، الطلبات المتبقية تتعلق بالسلع التي لا نملكها على النظام الأساسي. زاد أيضًا عدد الجلسات بدون استعلام بحث ثاني (والعديد من المقاييس الأخرى من هذا النوع مرتبطة بـ UX). ومع ذلك ، لم تتغير المقاييس المتعلقة بالمال بشكل كبير - فقد كان هذا غير متوقع وقادنا إلى تحليل شامل ومراجعة مقاييس أخرى.

الخاتمة

أخبر ستيفن هوكينج ذات مرة أن كل صيغة أدرجها في الكتاب ستقلل من عدد القراء إلى النصف. حسنًا ، يوجد في هذا المقال حوالي خمسين منهم - أهنئكم ، أحدهم$$من 10 إلى 10 قراء وصلوا إلى هذا المكان!$10^{-10}$

مكافأة

المراجع

[1] إم دي كيرنيغان ، كنيسة كي دبليو ، واشنطن. برنامج لتصحيح الإملاء بناءً على نموذج قناة صاخبة . وقائع المؤتمر الثالث عشر حول اللغويات الحاسوبية - المجلد 2 ، 1990.

[2] E.Brill ، RC Moore. نموذج خطأ محسّن لتصحيح تهجئة القناة الصاخبة . وقائع الاجتماع السنوي الثامن والثلاثين حول رابطة اللغويات الحاسوبية ، 2000.

[3] T. Brants، AC Popat، P. Xu، FJ Och، J. Dean. نماذج اللغة الكبيرة في الترجمة الآلية . وقائع مؤتمر 2007 حول الأساليب التجريبية في معالجة اللغة الطبيعية.

[4] سي وايتلو ، ب. هتشينسون ، جي. تشونج ، ج. إليس. استخدام الويب للتدقيق الإملائي المستقل للغة و التصحيح التلقائي. وقائع مؤتمر عام 2009 حول الأساليب التجريبية في معالجة اللغة الطبيعية: المجلد 2.