أداء مذهل لخوارزميات C ++ 17 المتوازية. أسطورة أم حقيقة؟

مساء الخير

من خلال دورتنا "C ++ Developer" ، نقدم لك دراسة صغيرة ومثيرة للاهتمام حول الخوارزميات المتوازية.

دعنا نذهب.

مع ظهور خوارزميات متوازية في C ++ 17 ، يمكنك بسهولة تحديث رمز "الحوسبة" والاستفادة من التنفيذ المتوازي. في هذه المقالة ، أريد أن أعتبر خوارزمية STL ، والتي تكشف بشكل طبيعي عن فكرة الحوسبة المستقلة. هل يمكن أن نتوقع تسارع 10x مع معالج 10 النواة؟ أو ربما أكثر؟ او اقل؟ دعنا نتحدث عن ذلك.

مقدمة في الخوارزميات المتوازية



يقدم C ++ 17 إعداد سياسة تنفيذ لمعظم الخوارزميات:

• sequenced_policy - نوع سياسة التنفيذ ، يستخدم كنوع فريد للتخلص من التحميل الزائد للخوارزمية المتوازية وشرط أن موازاة تنفيذ الخوارزمية المتوازية أمر مستحيل: الكائن العمومي المقابل هو std::execution::seq ؛
• parallel_policy - نوع سياسة التنفيذ المستخدم كنوع فريد للتخلص من التحميل الزائد للخوارزمية المتوازية والإشارة إلى أن موازاة تنفيذ الخوارزمية المتوازية أمر ممكن: الكائن العمومي المقابل هو std::execution::par ؛
• parallel_unsequenced_policy - نوع من سياسة التنفيذ يستخدم كنوع فريد للتخلص من التحميل الزائد للخوارزمية المتوازية والإشارة إلى أن التوازي مع ناقل تنفيذ الخوارزمية المتوازية أمران ممكنان: الكائن العمومي المقابل هو std::execution::par_unseq ؛

باختصار:

• استخدم std::execution::seq للتنفيذ المتسلسل للخوارزمية ؛
• استخدم std::execution::par لتنفيذ الخوارزمية بشكل متواز (عادةً ما يستخدم بعض تطبيق Thread Pool (مؤشر ترابط))؛
• استخدم std::execution::par_unseq للتنفيذ المتوازي للخوارزمية مع القدرة على استخدام أوامر vector (على سبيل المثال ، SSE ، AVX).

كمثال سريع ، اتصل std::sort بالتوازي:

 std::sort(std::execution::par, myVec.begin(), myVec.end()); // ^^^^^^^^^^^^^^^^^^^ //   

لاحظ مدى سهولة إضافة معلمة تنفيذ موازية إلى الخوارزمية! ولكن هل سيتم تحقيق تحسن كبير في الأداء؟ هل ستزيد السرعة؟ أم أن هناك أي تباطؤ؟

std::transform بالتوازي std::transform

في هذه المقالة ، أود الانتباه إلى خوارزمية std::transform_reduce for_each ، والتي من المحتمل أن تكون أساسًا للطرق الموازية الأخرى (جنبًا إلى جنب مع std::transform_reduce for_each ، for_each ، scan ، sort ...).

سيتم بناء رمز الاختبار الخاص بنا وفقًا للقالب التالي:

 std::transform(execution_policy, // par, seq, par_unseq inVec.begin(), inVec.end(), outVec.begin(), ElementOperation); 

لنفترض أن وظيفة ElementOperation لا تحتوي على طرق التزامن ، وفي هذه الحالة يكون للشفرة إمكانية التنفيذ المتوازي أو حتى الاتجاه. كل حساب عنصر مستقل ، لا يهم الترتيب ، لذلك يمكن للتنفيذ أن يولد عدة مؤشرات ترابط (ربما في تجمع مؤشرات ترابط) للمعالجة المستقلة للعناصر.

أود تجربة الأشياء التالية:

• حجم مجال المتجه كبير أو صغير ؛
• تحويل بسيط يمضي معظم الوقت في الوصول إلى الذاكرة ؛
• المزيد من العمليات الحسابية (ALU) ؛
• ALU في سيناريو أكثر واقعية.

كما ترون ، لا أريد فقط اختبار عدد العناصر "الجيدة" لاستخدام الخوارزمية المتوازية ، ولكن أيضًا عمليات ALU التي تشغل المعالج.
الخوارزميات الأخرى ، مثل الفرز والتراكم (في شكل الأمراض المنقولة جنسيا :: تقليل) تقدم أيضا تنفيذ مواز ، ولكنها تتطلب أيضا المزيد من العمل لحساب النتائج. لذلك ، سوف نعتبرهم مرشحين لمقال آخر.

ملاحظة المعيار

بالنسبة لاختباراتي ، أستخدم Visual Studio 2017 ، 15.8 - نظرًا لأن هذا هو التطبيق الوحيد في تطبيق برنامج التحويل البرمجي الشهير / STL في الوقت الحالي (نوفمبر ، 2018) (دول مجلس التعاون الخليجي في الطريق!). علاوة على ذلك ، ركزت فقط على execution::par ، لأن execution::par_unseq متوفر في MSVC (يعمل بشكل مشابه execution::par ).

يوجد جهازي كمبيوتر:

• i7 8700 - PC، Windows 10، i7 8700 - 3.2 GHz، 6 خيوط / 12 محور (Hyperthreading)؛
• i7 4720 - الكمبيوتر المحمول ، ويندوز 10 ، i7 4720 ، 2.6 جيجاهرتز ، 4 نوى / 8 سلاسل (Hyperthreading).

يتم تجميع الشفرة في x64 ، الإصدار أكثر ، يتم تمكين ناقل تلقائي بشكل افتراضي ، كما قمت بتضمين مجموعة موسعة من الأوامر (SSE2) و OpenMP (2.0).

الكود موجود في github: github / fenbf / ParSTLTests / TransformTests / TransformTests.cpp

بالنسبة لبرنامج OpenMP (2.0) ، استخدم التوازي فقط للحلقات:

 #pragma omp parallel for for (int i = 0; ...) 

أركض الكود 5 مرات وانظر إلى الحد الأدنى من النتائج.

تحذير : تعكس النتائج ملاحظات تقريبية فقط ؛ تحقق من النظام / التكوين قبل الاستخدام في الإنتاج. الاحتياجات الخاصة بك والمناطق المحيطة بها قد تختلف عن بلدي.

يمكنك قراءة المزيد حول تطبيق MSVC في هذا المنشور. وإليكم آخر تقرير لبيل أونيل مع CppCon 2018 (قام بيل بتنفيذ STL الموازي في MSVC).

حسنًا ، لنبدأ بأمثلة بسيطة!

تحويل بسيط

ضع في اعتبارك الحالة عند تطبيق عملية بسيطة للغاية على ناقل الإدخال. يمكن أن يكون نسخ أو ضرب العناصر.

على سبيل المثال:

 std::transform(std::execution::par, vec.begin(), vec.end(), out.begin(), [](double v) { return v * 2.0; } ); 

يشتمل جهاز الكمبيوتر الخاص بي على 6 أو 4 مراكز ... هل يمكنني توقع تنفيذ تسلسلي 4..6x بشكل أسرع؟ فيما يلي نتائجي (الوقت بالميلي ثانية):

العملية	حجم المتجهات	i7 4720 (4 النوى)	i7 8700 (6 النوى)
التنفيذ ::	10 ك	0.002763	0.001924
التنفيذ :: الاسم	10 ك	0.009869	0.008983
openmp موازية ل	10 ك	0.003158	0.002246
التنفيذ ::	100 ك	0.051318	0.028872
التنفيذ :: الاسم	100 ك	0.043028	0.025664
openmp موازية ل	100 ك	0.022501	0.009624
التنفيذ ::	1000 ك	1.69508	0.52419
التنفيذ :: الاسم	1000 ك	1.65561	0.359619
openmp موازية ل	1000 ك	1.50678	0.344863

على جهاز أسرع ، يمكننا أن نرى أن الأمر سيستغرق حوالي مليون عنصر لملاحظة تحسن الأداء. من ناحية أخرى ، كانت جميع التطبيقات المتوازية أبطأ على جهاز الكمبيوتر المحمول.

وبالتالي ، من الصعب ملاحظة أي تحسن كبير في الأداء باستخدام مثل هذه التحويلات ، حتى مع زيادة عدد العناصر.

لماذا هكذا؟

نظرًا لأن العمليات أولية ، يمكن لقلب المعالج أن يسميها على الفور تقريبًا ، وذلك باستخدام بضع دورات فقط. ومع ذلك ، فإن قلوب المعالج تقضي وقتًا أكبر في انتظار الذاكرة الرئيسية. لذلك ، في هذه الحالة ، في معظم الأحيان سوف ينتظرون ، وليس إجراء حسابات.

قراءة وكتابة متغير في الذاكرة يستغرق حوالي 2-3 دورات إذا تم تخزينه مؤقتًا ، ومئات الدورات إذا لم يتم تخزينه مؤقتًا.
https://www.agner.org/optimize/optimizing_cpp.pdf

يمكنك ملاحظة أنه إذا كانت الخوارزمية تعتمد على الذاكرة ، فيجب ألا تتوقع تحسينات في الأداء باستخدام الحوسبة المتوازية.

المزيد من الحسابات

نظرًا لأن عرض النطاق الترددي للذاكرة أمر حاسم ويمكن أن يؤثر على سرعة الأشياء ... فلنزيد من مقدار الحساب الذي يؤثر على كل عنصر.

الفكرة هي أنه من الأفضل استخدام دورات المعالج بدلاً من إضاعة الوقت في انتظار الذاكرة.

بادئ ذي بدء ، يمكنني استخدام الدوال المثلثية ، على سبيل المثال ، sqrt(sin*cos) (هذه حسابات شرطية في شكل غير مثالي ، فقط لشغل المعالج).

نحن نستخدم sqrt ، و sin ، و cos ، والتي يمكن أن تأخذ ~ 20 لكل sqrt و ~ 100 لكل وظيفة مثلثية. هذا المبلغ من حساب يمكن أن تغطي تأخير وصول الذاكرة.

لمزيد من المعلومات حول تأخيرات الفريق ، راجع دليل Perf الممتاز من Agner Fogh .

هنا هو رمز الاختبار:

 std::transform(std::execution::par, vec.begin(), vec.end(), out.begin(), [](double v) { return std::sqrt(std::sin(v)*std::cos(v)); } ); 

والآن ماذا؟ هل يمكننا الاعتماد على تحسين الأداء مقارنة بالمحاولة السابقة؟

فيما يلي بعض النتائج (الوقت بالميلي ثانية):

العملية	حجم المتجهات	i7 4720 (4 النوى)	i7 8700 (6 النوى)
التنفيذ ::	10 ك	0.105005	0.070577
التنفيذ :: الاسم	10 ك	0.055661	0.03176
openmp موازية ل	10 ك	0.096321	0.024702
التنفيذ ::	100 ك	1.08755	0.707048
التنفيذ :: الاسم	100 ك	0.259354	0.17195
openmp موازية ل	100 ك	0.898465	0.189915
التنفيذ ::	1000 ك	10.5159	7.16254
التنفيذ :: الاسم	1000 ك	2.44472	1.10099
openmp موازية ل	1000 ك	4.78681	1.89017

وأخيرا ، نرى أرقام لطيفة :)

بالنسبة إلى 1000 عنصر (غير معروض هنا) ، كانت أوقات الحساب المتوازية والمتسلسلة متشابهة ، لذلك نرى أكثر من 1000 عنصر نشهد تحسناً في الإصدار المتوازي.

بالنسبة لـ 100 ألف عنصر ، تكون النتيجة على جهاز كمبيوتر أسرع أفضل تقريبًا 9 مرات من الإصدار التسلسلي (على نحو مماثل لإصدار OpenMP).

في أكبر إصدار من مليون عنصر ، تكون النتيجة أسرع 5 أو 8 مرات.
بالنسبة لهذه الحسابات ، حققت تسارعًا "خطيًا" ، اعتمادًا على عدد مراكز المعالج. الذي كان متوقعا.

فريسنل وناقلات ثلاثية الأبعاد

في القسم أعلاه ، استخدمت الحسابات "المخترعة" ، لكن ماذا عن الكود الحقيقي؟
دعونا نحل معادلات فريسنل التي تصف انعكاس وانحناء الضوء من سطح أملس مسطح. هذه طريقة شائعة لتوليد إضاءة واقعية في الألعاب ثلاثية الأبعاد.




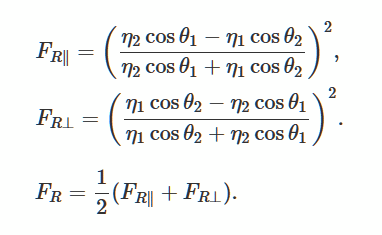
صور من ويكيميديا

كمثال جيد ، لقد وجدت هذا الوصف والتنفيذ .

حول استخدام مكتبة GLM

بدلاً من إنشاء تطبيقي الخاص ، استخدمت مكتبة glm . أستخدمه غالبًا في مشاريع OpenGl الخاصة بي.

يمكن الوصول إلى المكتبة بسهولة من خلال Conan Package Manager ، لذلك سأستخدمها أيضًا. رابط إلى الحزمة.

ملف كونان:

 [requires] glm/0.9.9.1@g-truc/stable [generators] visual_studio 

وسطر الأوامر لتثبيت المكتبة (يقوم بإنشاء ملفات الدعائم التي يمكنني استخدامها في مشروع Visual Studio):

 conan install . -s build_type=Release -if build_release_x64 -s arch=x86_64 

تتكون المكتبة من رأس ، بحيث يمكنك تنزيلها يدويًا إذا أردت.

الرمز الفعلي والمعيار

لقد قمت بتكييف رمز glm من scratchapixel.com :

 //    https://www.scratchapixel.com float fresnel(const glm::vec4 &I, const glm::vec4 &N, const float ior) { float cosi = std::clamp(glm::dot(I, N), -1.0f, 1.0f); float etai = 1, etat = ior; if (cosi > 0) { std::swap(etai, etat); } //  sini     float sint = etai / etat * sqrtf(std::max(0.f, 1 - cosi * cosi)); //    if (sint >= 1) return 1.0f; float cost = sqrtf(std::max(0.f, 1 - sint * sint)); cosi = fabsf(cosi); float Rs = ((etat * cosi) - (etai * cost)) / ((etat * cosi) + (etai * cost)); float Rp = ((etai * cosi) - (etat * cost)) / ((etai * cosi) + (etat * cost)); return (Rs * Rs + Rp * Rp) / 2.0f; } 

يستخدم الرمز العديد من الإرشادات الرياضية ، والمنتج القياسي ، والضرب ، والقسمة ، وبالتالي فإن المعالج لديه ما يفعله. بدلاً من الموجه المزدوج ، نستخدم متجهًا يتكون من 4 عناصر لزيادة مقدار الذاكرة المستخدمة.

المعيار:

 std::transform(std::execution::par, vec.begin(), vec.end(), vecNormals.begin(), //   vecFresnelTerms.begin(), //  [](const glm::vec4& v, const glm::vec4& n) { return fresnel(v, n, 1.0f); } ); 

وهنا النتائج (الوقت بالميلي ثانية):

العملية	حجم المتجهات	i7 4720 (4 النوى)	i7 8700 (6 النوى)
التنفيذ ::	1 ك	0.032764	0.016361
التنفيذ :: الاسم	1 ك	0.031186	0.028551
openmp موازية ل	1 ك	0.005526	0.007699
التنفيذ ::	10 ك	0.246722	0.169383
التنفيذ :: الاسم	10 ك	0.090794	0.067048
openmp موازية ل	10 ك	0.049739	0.029835
التنفيذ ::	100 ك	2.49722	1.69768
التنفيذ :: الاسم	100 ك	0.530157	0.283268
openmp موازية ل	100 ك	0.495024	0.291609
التنفيذ ::	1000 ك	08/25/28	16.9457
التنفيذ :: الاسم	1000 ك	5.15235	2.33768
openmp موازية ل	1000 ك	5.11801	2.95908

باستخدام الحوسبة "الحقيقية" ، نرى أن الخوارزميات المتوازية توفر أداءً جيدًا. بالنسبة لهذه العمليات على جهازي Windows ، حققت تسارعًا مع اعتماد خطي تقريبًا على عدد النوى.

بالنسبة لجميع الاختبارات ، أظهرت أيضًا نتائج من OpenMP وتطبيقين: يعمل MSVC و OpenMP بشكل مشابه.

الخاتمة

في هذه المقالة ، نظرت إلى ثلاث حالات لاستخدام خوارزميات الحوسبة المتوازية والخوارزميات المتوازية. قد يبدو استبدال الخوارزميات القياسية بالإصدار std :: implementation :: par مغريًا للغاية ، لكن هذا لا يستحق دائمًا القيام به! قد تعمل كل عملية تستخدمها داخل الخوارزمية بشكل مختلف وتكون أكثر اعتمادًا على المعالج أو الذاكرة. لذلك ، فكر في كل تغيير على حدة.

أشياء يجب تذكرها:

• التنفيذ المتوازي ، عادة ، يفعل أكثر من تسلسلي ، حيث يجب أن تستعد المكتبة للتنفيذ المتوازي ؛
• ليس فقط عدد العناصر أمر مهم ، ولكن أيضًا عدد الإرشادات التي يشغلها المعالج ؛
• من الأفضل القيام بمهام مستقلة عن بعضها البعض وعن الموارد المشتركة الأخرى ؛
• توفر الخوارزميات المتوازية طريقة سهلة لتقسيم العمل إلى مؤشرات ترابط منفصلة ؛
• إذا كانت عملياتك تعتمد على الذاكرة ، يجب ألا تتوقع تحسينات في الأداء ، وفي بعض الحالات ، قد تكون الخوارزميات أبطأ ؛
• للحصول على تحسين أداء لائق ، قم دائمًا بقياس توقيت كل مشكلة ، وفي بعض الحالات قد تكون النتائج مختلفة تمامًا.

شكر خاص إلى JFT للمساعدة في هذا المقال!

انتبه أيضًا إلى مصادري الأخرى حول الخوارزميات المتوازية:

• فصل حديث في كتابي C ++ 17 In Detail حول الخوارزميات المتوازية ؛
• STL الموازي و نظام الملفات: ملفات مثال على عدد الكلمات ؛
• أمثلة للخوارزميات المتوازية من C ++ 17 .

ألقِ نظرة على مقالة أخرى تتعلق بالخوارزميات المتوازية: كيفية زيادة الأداء باستخدام خوارزميات Parallel STL و C ++ 17 من Intel

النهاية

نحن في انتظار التعليقات والأسئلة التي يمكنك تركها هنا أو في مدرسنا على الباب المفتوح .