شبكات كثافة الخليط

مرحبا بالجميع!

لنتحدث عن الشبكات العصبية والتعلم الآلي ، كما قد تفكر. من الواضح أن ما سيتم إخبارك به حول شبكات Mixture Density Networks ، ثم MDN فقط ، لا أريد ترجمة الاسم وتركه كما هو. نعم ، نعم ، نعم ... سيكون هناك القليل من الرياضيات ونظرية الاحتمالات المملة ، ولكن بدونها ، لسوء الحظ ، أو لحسن الحظ ، يعود الأمر لك لتقرير ما إذا كان من الصعب تخيل عالم التعلم الآلي. لكنني أسارع إلى طمأنتك ، ستكون صغيرة نسبيًا ولن تكون صعبة للغاية. على أي حال ، يمكنك تخطي ذلك ، لكن انظر فقط إلى كمية صغيرة من التعليمات البرمجية في Python و PyTorch ، هذا صحيح ، سنكتب الشبكة باستخدام PyTorch ، بالإضافة إلى الرسوم البيانية المختلفة مع النتائج. ولكن الشيء الأكثر أهمية هو أنه ستكون هناك فرصة لفهم القليل وفهم ما هي شبكات MD.

حسنًا ، لنبدأ!

---

الانحدار

بادئ ذي بدء ، دعنا نجدد معرفتنا قليلاً ونتذكر ، باختصار شديد ، ما هو الانحدار الخطي .

لدينا ناقلات $$$X = \ {x_1 ، x_2 ، ... ، x_n \}$ نحن بحاجة إلى التنبؤ القيمة $$$Y$ ، والتي تعتمد بطريقة أو بأخرى على $$$X$ باستخدام بعض النماذج الخطية:

$$

$$\ hat {Y} = X ^ T \ hat {\ beta}$$

كدالة خطأ ، سوف نستخدم الخطأ التربيعي:

$$

$$SE (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 = \ sum_ {i = 1} ^ N (y_i-x_i ^ T \ hat {\ beta} ) ^ 2$$

يمكن حل هذه المشكلة مباشرة عن طريق أخذ مشتق SE وتحديد قيمته على الصفر:

$$

$$\ frac {\ delta SE (\ beta)} {\ delta \ beta} = 2X ^ T (\ mathbf {y} -X \ beta) = 0$$

وبالتالي ، نجد ببساطة الحد الأدنى ، و SE هي وظيفة من الدرجة الثانية ، مما يعني أن الحد الأدنى سيكون موجودًا دائمًا. بعد ذلك ، يمكنك بالفعل العثور بسهولة $$$\ beta$ :

$$

$$\ hat \ beta = (X ^ TX) ^ {- 1} X ^ T \ mathbf {y}$$

هذا كل شيء ، تم حل المشكلة. هذا هو المكان الذي ننهي فيه تذكر ما هو الانحدار الخطي.

بالطبع ، يمكن أن يكون الاعتماد الملازم لطبيعة توليد البيانات مختلفًا ومن ثم يجب إضافة بعض اللاخطية بالفعل إلى نموذجنا. يعد حل مشكلة الانحدار مباشرةً للبيانات الكبيرة والحقيقية فكرة سيئة ، نظرًا لوجود مصفوفة $$$X ^ TX$ الأبعاد $$$n \ مرة n$ ، ولا يزال يحتاج المرء إلى العثور على مصفوفة معكوس ، وغالبا ما يحدث أن مثل هذه المصفوفة ببساطة غير موجودة. في هذه الحالة ، فإن الطرق المختلفة التي تعتمد على النسب المتدرج تأتي لمساعدتنا. يمكن تطبيق عدم خطية النماذج بطرق مختلفة ، بما في ذلك استخدام الشبكات العصبية.

ولكن الآن ، دعونا نتحدث ليس عن هذا ، ولكن عن وظائف الخطأ. ما هو الفرق بين SE و Log-مرجح عندما يمكن أن يكون للبيانات علاقة غير خطية؟


توقف عن ذلك! احتمال؟ هذا شيء من نظرية الاحتمالات. هذا صحيح - إنها نظرية احتمال محضة. ولكن كيف يمكن أن يرتبط الانحراف التربيعي بوظيفة الاحتمال؟ وكيف اتضح. إنه مرتبط بإيجاد الاحتمال الأقصى (الاحتمالية القصوى) والتوزيع الطبيعي ، ليكون أكثر دقة ، بمتوسطه $$$\ mu$ .

من أجل إدراك أن هذا صحيح ، دعنا ننظر مرة أخرى إلى وظيفة الانحراف المربعي:

$$

$$RSS (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 \ qquad \ qquad (1)$$

لنفترض الآن أن وظيفة الاحتمال لها شكل عادي ، أي توزيع غاوسي أو عادي:

$$

$$L (X) = p (X | \ theta) = \ prod ^ X \ mathcal {N} (x_i؛ \ mu، \ sigma ^ 2)$$

بشكل عام ، ما هي وظيفة الاحتمال وما هو المعنى الذي لن أقوله ، يمكنك أن تقرأ عنها في مكان آخر ، وعليك أيضًا أن تتعرف على مفهوم الاحتمال المشروط ، ونظرية بايز ، وأكثر من ذلك بكثير ، لفهم أعمق. كل هذا يذهب إلى نظرية الاحتمال البحتة ، والتي تدرس في المدرسة والجامعة.

الآن ، مع تذكر صيغة التوزيع العادية ، نحصل على:

$$

$$L (X؛ \ mu، \ sigma ^ 2) = \ prod ^ X \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {(x_i- \ mu) ^ 2} {2 \ sigma ^ 2}} \ qquad \ qquad (2)$$

ماذا لو وضعنا الانحراف المعياري $$$\ sigma ^ 2 = 1$ وإزالة جميع الثوابت في الصيغة (2) ، فقط قم بإزالة ، لا تقلل ، لأن العثور على الحد الأدنى من الوظيفة لا يعتمد عليها. ثم سوف نرى هذا:

$$

$$L (X؛ \ mu، \ sigma ^ 2) \ sim \ prod ^ Xe ^ {- (x_i- \ mu) ^ 2}$$

لا يزال لا شيء مثل؟ لا؟ حسنا ، ماذا لو أخذنا لوغاريتم الوظيفة؟ من اللوغاريتم ، بشكل عام ، هناك بعض الإيجابيات: الضرب سوف يتحول إلى مبلغ ، درجة إلى ضرب ، و $$$\ log {e} = 1$ - بالنسبة لهذه الخاصية ، تجدر الإشارة إلى أننا نتحدث عن اللوغاريتم الطبيعي ، وبشكل صارم $$$\ ln {e} = 1 دولا$ . وبشكل عام ، لا يغير لوغاريتم الوظيفة حدها الأقصى ، وهذه هي أهم ميزة بالنسبة لنا. سيتم وصف الارتباط مع احتمال الأرجحية والاحتمالية ولماذا سيكون ذلك مفيدًا أدناه في انحدار صغير. وهكذا فعلنا: أزلنا جميع الثوابت ، وأخذنا لوغاريتم دالة الاحتمالية. لقد قاموا أيضًا بإزالة علامة الطرح ، وبالتالي تحويل "احتمال الدخول" إلى "احتمال الدخول السلبي" (NLL) ، كما سيتم وصف العلاقة بينهما كمكافأة. نتيجة لذلك ، حصلنا على وظيفة NLL:

$$

$$\ log L (X؛ \ mu، I ^ 2) \ sim \ sum (X- \ mu) ^ 2$$

ألق نظرة أخرى على وظيفة RSS (1). نعم ، هم نفس الشيء! بالضبط! وينظر أيضا ذلك $$$\ mu = \ hat {y}$ .

إذا كنت تستخدم دالة الانحراف المعياري لـ MSE ، فسنحصل على ما يلي:

$$

$$\ operatorname {argmin} MSE (\ beta) \ sim \ operatorname {argmax} \ mathbb {E} _ {X \ sim P_ {data}} \ log P_ {model} (x؛ \ beta)$$

اين $$$\ mathbb {E}$ - التوقع الرياضي $$$\ beta$ - معلمات النموذج ، في المستقبل سوف نشير إليها على النحو التالي: $$$\ theta$ .

الخلاصة: إذا استخدمنا عائلة LS كدالة للخطأ في سؤال الانحدار ، فنحن نحل بشكل أساسي مشكلة إيجاد الحد الأقصى لوظيفة الاحتمال في الحالة التي يكون فيها التوزيع غاوسي. والقيمة المتوقعة $$$\ hat {y}$ يساوي المتوسط ​​في التوزيع الطبيعي. والآن نحن نعرف كيف يرتبط كل هذا ، وكيف ترتبط نظرية الاحتمالات (مع وظيفة الاحتمال والتوزيع الطبيعي) وطرق الانحراف المعياري أو OLS. يمكن العثور على مزيد من التفاصيل حول هذا في [2].

وهنا المكافأة الموعودة. نظرًا لأننا نتحدث عن العلاقات بين وظائف الخطأ المختلفة ، فسوف نأخذ في الاعتبار (ليس بالضرورة قراءتها):

انحدار الشبكة العصبية

لذلك وصلنا إلى ممارسة أكثر إثارة للاهتمام. دعونا نرى كيف يمكنك حل مشكلة الانحدار باستخدام الشبكات العصبية (الشبكات العصبية). سننفذ كل شيء في لغة برمجة Python ، لإنشاء شبكة نستخدم مكتبة PyTorch للتعلم العميق.

توليد البيانات المصدر

إدخال البيانات $$$\ mathbf {X} \ in \ mathbb {R} ^ N$ توليد باستخدام توزيع موحد ، تأخذ الفاصل الزمني من -15 إلى 15 ، $$$\ mathbf {X} \ in U [-15، 15]$ . نقاط $$$\ mathbf {Y}$ نحصل عليها باستخدام المعادلة:

$$

$$\ mathbf {Y} = 0.5 \ mathbf {X} + 8 \ sin (0.3 \ mathbf {X}) + noise \ qquad \ qquad (3)$$

اين $$$الضوضاء$ هو ناقل الضوضاء البعد $$$N$ تم الحصول عليها باستخدام التوزيع الطبيعي مع المعلمات: $$$\ mu = 0 ، \ sigma ^ 2 = 1$ .



الرسم البياني للبيانات المستلمة.

بناء الشبكة

إنشاء شبكة تغذية عصبية إلى الأمام العادية أو FFNN.


تتكون شبكتنا من طبقة واحدة مخفية بأبعاد من 40 خلية عصبية مع وظيفة تنشيط - الظل الزائدي:

$$

$$\ tanh x = \ frac {e ^ x-e ^ {- x}} {e ^ x + e ^ {- x}} \ qquad \ qquad (4)$$

طبقة الخرج عبارة عن تحويل خطي عادي بدون وظيفة تنشيط.

التعلم والحصول على النتائج

كمحسن سوف نستخدم AdamOptimizer. عدد مرات الدراسة = 2000 ، معدل التعلم (معدل التعلم أو التعلم) = 0.1.


الآن دعونا نلقي نظرة على نتائج التعلم.


رسم بياني لقيم وظيفة MSE اعتمادًا على تكرار التدريب ؛ رسم بياني لقيم بيانات التدريب وبيانات الاختبار.


النتائج الحقيقية والمتوقعة على بيانات الاختبار.

البيانات المقلوبة

نحن تعقيد المهمة وعكس البيانات.



الرسم البياني للبيانات المقلوبة.

للتنبؤ $$$\ mathbf {\ hat Y}$ دعنا نستخدم شبكة التوزيع المباشر من القسم السابق ونرى كيف تعالج هذا.

 inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv) 

رسم بياني لقيم وظيفة MSE اعتمادًا على تكرار التدريب ؛ رسم بياني لقيم بيانات التدريب وبيانات الاختبار.


النتائج الحقيقية والمتوقعة على بيانات الاختبار.

كما ترون من الرسوم البيانية أعلاه ، فإن شبكتنا لم تتعامل مع هذه البيانات على الإطلاق ، فهي ببساطة غير قادرة على التنبؤ بها. وحدث كل هذا لأنه في مثل هذه المشكلة المقلوبة لنقطة واحدة $$$x$ قد تتوافق مع عدة نقاط $$$ذ$ . أنت تسأل ، ماذا عن الضوضاء؟ انه خلق أيضا موقف فيه لأحد $$$x$ يمكن الحصول على بعض القيم $$$ذ$ . نعم هذا صحيح. لكن بيت القصيد هو أنه ، على الرغم من الضوضاء ، كان كل توزيع واحد واضح. وبما أن نموذجنا تنبأ بشكل أساسي $$$p (y | x)$ وفي حالة MSE ، كان متوسط ​​قيمة التوزيع الطبيعي (لماذا هو موصوف في الجزء الأول من المقالة) ، ثم تعامل بشكل جيد مع المهمة "المباشرة". خلاف ذلك ، نحصل على عدة توزيعات مختلفة لواحد $$$x$ وبناءً على ذلك ، لا يمكننا الحصول على نتيجة جيدة بتوزيع واحد عادي فقط.

شبكة كثافة الخليط

المرح يبدأ! ما هي شبكة Mixture Density (فيما يلي شبكة MDN أو MD)؟ بشكل عام ، هذا نموذج معين قادر على محاكاة عدة توزيعات في وقت واحد:

$$

$$p (\ mathbf {y} | \ mathbf {x}؛ \ theta) = \ sum_k ^ K \ pi_k (\ mathbf {x}) \ mathcal {N} (\ mathbf {y}؛ \ mu_k (\ mathbf { x}) ، \ sigma ^ 2 (\ mathbf {x})) \ qquad \ qquad (5)$$

يا له من صيغة غريبة ، كما تقول. دعونا معرفة ذلك. تتعلم شبكة MD لدينا نمذجة الوسط $$$\ mu$ والتباين $$$\ سيجما ^ 2$ لتوزيعات متعددة . في الصيغة (5) $$$\ pi_k (\ mathbf {x})$ - ما يسمى عوامل الأهمية لتوزيع منفصل لكل نقطة $$$x_i \ in \ mathbf {x}$ ، عامل خلط معين ، أو مقدار مساهمة كل من التوزيعات في نقطة معينة. المجموع هناك $$$K$ توزيعات.

بضع كلمات أخرى عنه $$$\ pi_k (\ mathbf {x})$ - في الواقع ، هذا هو أيضا توزيع ويمثل الاحتمال أن نقطة $$$x_i \ in \ mathbf {x}$ سوف يكون شرطا $$$ك$ .

فوه ، مرة أخرى ، هذه الرياضيات ، دعنا نكتب شيئًا بالفعل. وهكذا ، سوف نبدأ في تحقيق شبكة. لشبكتنا نأخذ $$$ك = 30 دولا$ .

 self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance 

حدد طبقات الإخراج لشبكتنا:

 x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) 

نكتب وظيفة الخطأ أو وظيفة الخسارة ، الصيغة (5):

 def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) 

شبكة MD لدينا جاهزة للعمل. جاهز تقريبا. يبقى لتدريبها والنظر في النتائج.



الرسم البياني لقيم دالة الخسارة اعتمادًا على تكرار التدريب ؛ الرسم البياني لقيم بيانات التدريب وبيانات الاختبار.

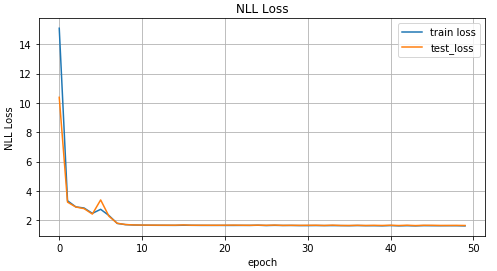
نظرًا لأن شبكتنا قد تعلمت القيم المتوسطة لعدة توزيعات ، فلنلقِ نظرة على هذا:

 pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) 

رسم بياني للقيمتين المتوسطتين الأكثر احتمالا لكل نقطة (يسار). الرسم البياني للقيم الأربعة على الأرجح تعني القيم لكل نقطة (يمين).


الرسم البياني لجميع القيم يعني لكل نقطة.

للتنبؤ بالبيانات ، سنختار عدة قيم بشكل عشوائي $$$\ mu$ و $$$\ سيجما ^ 2$ بناء على القيمة $$$\ pi_k (\ mathbf {x})$ . وبعد ذلك بناء عليها لإنشاء البيانات المستهدفة $$$\ hat {y}$ باستخدام التوزيع الطبيعي.



البيانات المتوقعة لمدة 10 القيم المحددة عشوائيا $$$\ mu$ و $$$\ سيجما ^ 2$ (يسار) واثنان (يمين).

من خلال الأرقام ، يمكن أن نرى أن MDN قامت بعمل ممتاز من خلال المهمة "العكسية".

باستخدام بيانات أكثر تعقيدا

دعونا نرى كيف تتعامل شبكة MD لدينا مع بيانات أكثر تعقيدًا ، مثل البيانات الحلزونية. معادلة دوامة القطعي في الإحداثيات الديكارتية:

$$

$$x = \ rho \ cos \ phi \\\ qquad \ qquad \ qquad \ qquad \ qquad \ qquad (6) \\ y = \ rho \ sin \ phi \\ $$

الرسم البياني للبيانات دوامة.

للمتعة ، دعنا نرى كيف ستتعامل شبكة التغذية المباشرة مع هذه المهمة.


كما هو متوقع ، شبكة Feed-Forward غير قادرة على حل مشكلة الانحدار لمثل هذه البيانات.

نحن نستخدم شبكة MD الموصوفة والمُنشأة مسبقًا للتدريب على البيانات الحلزونية.


قامت شبكة Mixture Density بعمل رائع في هذا الموقف.

الخاتمة

في بداية هذه المقالة ، ذكرنا أساسيات الانحدار الخطي. رأينا ذلك مشتركًا بين إيجاد المتوسط ​​للتوزيع الطبيعي و MSE. تفكيك كيفية اتصال NLL وعبر إنتروبيا. والأهم من ذلك ، اكتشفنا نموذج MDN ، والذي هو قادر على التعلم من البيانات التي تم الحصول عليها من توزيع مختلط. آمل أن تكون المقالة مفهومة ومثيرة للاهتمام ، على الرغم من حقيقة وجود القليل من الرياضيات.

يمكن الاطلاع على الكود الكامل على جيثب .

---

الأدب

1. مزيج شبكات الكثافة (كريستوفر م. بيشوب ، مجموعة أبحاث الحوسبة العصبية ، قسم علوم الحاسوب والرياضيات التطبيقية ، جامعة أستون ، برمنغهام) - تصف المقالة بشكل كامل نظرية شبكات MD.
2. المربعات الصغرى والاحتمالية القصوى (MROsborne)