استخدام خريطة QML لبناء خطوط جوية - الجزء 1

منذ فترة طويلة الآن أستخدم QML لبناء واجهات رسومية ، لكن حتى الآن لم تكن هناك فرصة للعمل في مشروع حقيقي باستخدام واجهة برمجة تطبيقات Qt Location API وخريطة QML.
لذلك ، أصبح من المثير للاهتمام تجربة هذا المكون لبناء الشعب الهوائية.
تحت القاطع هو وصف لتطبيق المحرر ، لإنشاء مثل هذه المسارات على الخريطة:



لتبسيط التنفيذ ، تطير طائراتنا في الطائرة ثنائية الأبعاد بنفس الارتفاع. يتم تثبيت السرعة والحمل الزائد المسموح به - 920 كم / ساعة و 3 جم ، مما يعطي دائرة نصف قطرها تحول

$$

$$R = \ frac {v ^ 2} {G} = 21770 m$$

يتكون المسار من الأجزاء التالية:

حيث S هي بداية المناورة (هي نقطة الخروج من السابقة) ، M هي بداية المنعطف ، E هي المخرج منه ، و F هي النقطة الأخيرة (M للالتالي).

لحساب نقطة الدخول والخروج من المسار ، استخدمت معادلة المماس في الدائرة ، واتضح أن الحسابات كانت مرهقة إلى حد ما ، وأنا متأكد من أنه يمكن جعلها أكثر بساطة.

void Manoeuvre::calculate() { // General equation of line between first and middle points auto A = mStart.y() - mMiddle.y(); auto B = mMiddle.x() - mStart.x(); // Check cross product sign whether final point lies on left side auto crossProduct = (B*(mFinal.y() - mStart.y()) + A*(mFinal.x() - mStart.x())); // All three points lie on the same line if (isEqualToZero(crossProduct)) { mIsValid = true; mCircle = mExit = mMiddle; return; } mIsLeftTurn = crossProduct > 0; auto lineNorm = A*A + B*B; auto exitSign = mIsLeftTurn ? 1 : -1; auto projection = exitSign*mRadius * qSqrt(lineNorm); // Center lies on perpendicular to middle point if (!isEqualToZero(A) && !isEqualToZero(B)) { auto C = -B*mStart.y() - A*mStart.x(); auto right = (projection - C)/A - (mMiddle.x()*lineNorm + A*C) / (B*B); mCircle.ry() = right / (A/B + B/A); mCircle.rx() = (projection - B*mCircle.y() - C) / A; } else { // Entering line is perpendicular to either x- or y-axis auto deltaY = isEqualToZero(A) ? 0 : exitSign*mRadius; auto deltaX = isEqualToZero(B) ? 0 : exitSign*mRadius; mCircle.ry() = mMiddle.y() + deltaY; mCircle.rx() = mMiddle.x() + deltaX; } // Check if final point is outside manouevre circle auto circleDiffX = mFinal.x() - mCircle.x(); auto circleDiffY = mFinal.y() - mCircle.y(); auto distance = qSqrt(circleDiffX*circleDiffX + circleDiffY*circleDiffY); mIsValid = distance > mRadius; // Does not make sence to calculate futher if (!mIsValid) return; // Length of hypotenuse from final point to exit point auto beta = qAtan2(mCircle.y() - mFinal.y(), mCircle.x() - mFinal.x()); auto alpha = qAsin(mRadius / distance); auto length = qSqrt(distance*distance - mRadius*mRadius); // Depends on position of final point find exit point mExit.rx() = mFinal.x() + length*qCos(beta + exitSign*alpha); mExit.ry() = mFinal.y() + length*qSin(beta + exitSign*alpha); // Finally calculate start/span angles auto startAngle = qAtan2(mCircle.y() - mMiddle.y(), mMiddle.x() - mCircle.x()); auto endAngle = qAtan2(mCircle.y() - mExit.y(), mExit.x() - mCircle.x()); mStartAngle = startAngle < 0 ? startAngle + 2*M_PI : startAngle; endAngle = endAngle < 0 ? endAngle + 2*M_PI : endAngle; auto smallSpan = qFabs(endAngle - mStartAngle); auto bigSpan = 2*M_PI - qFabs(mStartAngle - endAngle); bool isZeroCrossed = mStartAngle > endAngle; if (!mIsLeftTurn) { mSpanAngle = isZeroCrossed ? bigSpan : smallSpan; } else { mSpanAngle = isZeroCrossed ? smallSpan : bigSpan; } } 

بعد الانتهاء من سوء تقدير النموذج الرياضي لمسارنا ، ننتقل إلى العمل مباشرة مع الخريطة. الخيار الطبيعي لبناء خطوط متعددة على خريطة QML هو إضافة MapPolyline مباشرة إلى الخريطة.

 Map { id: map plugin: Plugin { name: "osm" } MapPolyline { path: [ { latitude: -27, longitude: 153.0 }, ... ] } } 

في البداية ، أردت أن أتيح للمستخدم الفرصة لمحاكاة كل قسم لاحق من المسار "أثناء الطيران" - لإنشاء تأثير حركة المسار خلف المؤشر.



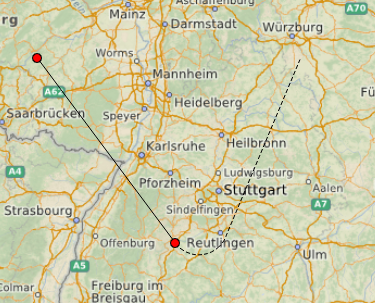
يعد تغيير المسار عند تحريك المؤشر عملية مكلفة إلى حد ما ، لذلك حاولت استخدام مسارات "البكسل" الأولية التي يتم عرضها حتى يقوم المستخدم في النهاية بحفظ المسار.

 Repeater { id: trajectoryView model: flightRegistry.hasActiveFlight ? flightRegistry.flightModel : [] FlightItem { anchors.fill: parent startPoint: start endPoint: end manoeuvreRect: rect manoeuvreStartAngle: startAngle manoeuvreSpanAngle: spanAngle isVirtualLink: isVirtual } } 

FlightItem هو QQuickItem ، ويتيح لك QAbstractListModel flightModel تحديث الأقسام اللازمة للمسار عند تغيير البيانات للمناورة.

 QVariant FlightModel::data(const QModelIndex &index, int role) const { if (!index.isValid()) { return QVariant(); } switch (role) { case FlightRoles::StartPoint: return mFlight->flightSegment(index.row()).line().p1(); case FlightRoles::EndPoint: return mFlight->flightSegment(index.row()).line().p2(); ... } 

يسمح لك هذا التحديث المباشر بتحذير المستخدم من المناورات غير القابلة للتحقيق.



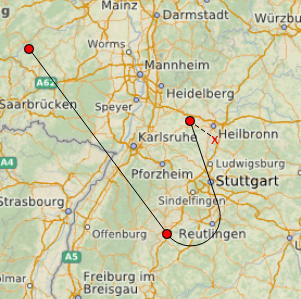
فقط بعد الانتهاء من إنشاء مجرى الهواء (على سبيل المثال ، مع النقر بالماوس الأيمن) ، ستتم إضافة المسار أخيرًا إلى خريطة QML باعتبارها GeoPath مع إمكانية الإشارة الجغرافية (حتى هذه اللحظة لا يمكن نقل الخريطة وتكبيرها / تصغيرها ، فإن البيكسلات لا تعرف شيئًا عن خطوط الطول والعرض).
لإعادة حساب قطعة البكسل في إحداثيات جغرافية ، بالنسبة للمبتدئين ، نحتاج إلى استخدام نظام إحداثي محلي لنقطة إدخال المناورة (النقطة S) لكل مناورة.

 QPointF FlightGeoRoute::toPlaneCoordinate(const QGeoCoordinate &origin, const QGeoCoordinate &point) { auto distance = origin.distanceTo(point); auto azimuth = origin.azimuthTo(point); auto x = qSin(qDegreesToRadians(azimuth)) * distance; auto y = qCos(qDegreesToRadians(azimuth)) * distance; return QPointF(x, y); } 

بعد إعادة حساب المناورة بالفعل ، يجب إجراء العملية العكسية ومعرفة الموقع الجغرافي للنقطة S لترجمة العدادات في خطوط الطول والعرض.

 QGeoCoordinate FlightGeoRoute::toGeoCoordinate(const QGeoCoordinate &origin, const QPointF &point) { auto distance = qSqrt(point.x()*point.x() + point.y()*point.y()); auto radianAngle = qAtan2(point.x(), point.y()); auto azimuth = qRadiansToDegrees(radianAngle < 0 ? radianAngle + 2*M_PI : radianAngle); return origin.atDistanceAndAzimuth(distance, azimuth); } 

من وجهة نظر رسمية ، من المستحيل ، بالطبع ، النظر في مسار "البكسل" و "العدادات" المطابقين ، لكن بدا لي أمرًا بالغًا بالنسبة لي أن أنظر إلى المستقبل وأظهر للمستخدم ما سيحدث (أو لن يحدث إذا لم تطير الطائرة بهذا الشكل) عندما سوف ينقر في المرة القادمة. بعد الانتهاء من المسار (يختلف قليلاً عن البيكسل في اللون والشفافية ، حيث أن الخطوط المكسورة الثابتة لا تبدو سلسة للغاية على الخريطة).



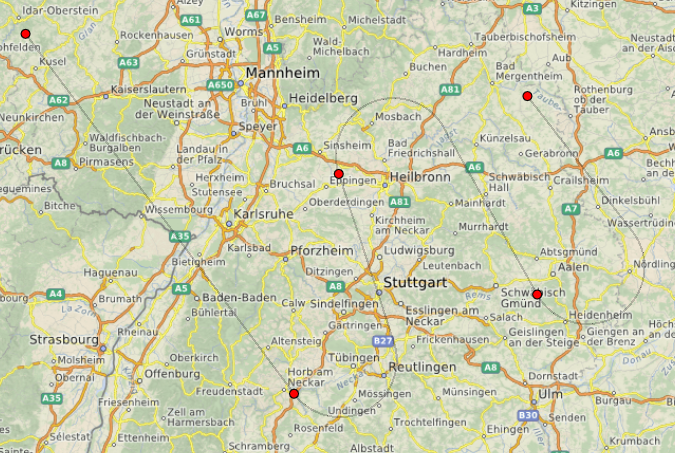
المصادر متوفرة هنا ؛ للتجميع استخدمت Qt 5.11.2.

في الجزء التالي ، سنقوم بتعليم محررنا لتحريك النقاط المرجعية للمسار ، وكذلك حفظ / فتح الطرق الحالية للمحاكاة اللاحقة لحركة الطائرات.