هذه هي المقالة الثانية حول تحليل ودراسة المواد من المسابقة للبحث عن السفن في البحر. ولكن الآن سوف ندرس خصائص متواليات التدريب. دعنا نحاول العثور على معلومات زائدة وتكرار في البيانات المصدر وحذفها.

هذه المقالة هي ببساطة نتيجة الفضول والاهتمام الخمول ، لم تتم مصادفة أي شيء منها في الممارسة ، ولا يوجد شيء تقريبًا للمهام العملية بالنسبة للنسخ واللصق. هذه دراسة صغيرة لخصائص التسلسل التدريبي - حيث يتم تقديم منطق المؤلف ورمزه ، يمكنك التحقق من / استكمال / تغيير كل شيء بنفسك.
انتهت المنافسة البحثية البحرية kaggle في الآونة الأخيرة. اقترحت إيرباص تحليل صور الأقمار الصناعية للبحر مع وبدون سفن. ما مجموعه 192555 صورة 768 × 768 × 3 - 340 720 680 960 بايت إذا كانت uint8 وهذه كمية كبيرة من المعلومات وكان هناك شك غامض في أنه ليست كل الصور مطلوبة لتدريب الشبكة وفي هذا الكم من المعلومات ، التكرار والتكرار واضحان. عند تدريب الشبكة ، من المعتاد فصل بعض البيانات وعدم استخدامها في التدريب ، ولكن استخدامها للتحقق من جودة التدريب. وإذا وقع واحد ونطاق البحر نفسه في صورتين مختلفتين وفي نفس الوقت سقطت إحدى الصور في تسلسل التدريب والأخرى في تسلسل التحقق ، فسيفقد التحقق معناه وسيتم إعادة تدريب الشبكة ، ولن نتحقق من قدرة الشبكة على تعميم المعلومات ، لأن البيانات هي نفسها. استغرق الكفاح ضد هذه الظاهرة الكثير من الوقت والجهد من GPU المشاركين. كالعادة ، لا يسارع الفائزون والفائزين بالجوائز إلى إظهار معجبيهم أسرار الإتقان ووضع الكود ، ولا توجد طريقة للدراسة والتعلم ، لذلك سنتناول النظرية.
أظهر الفحص البصري البسيط أنه يوجد بالفعل الكثير من البيانات ، فقد وقع نفس امتداد البحر في صور مختلفة ، وانظر إلى الأمثلة




ولهذا السبب ، نحن لسنا مهتمين بالبيانات الحقيقية ، فهناك الكثير من التبعيات الزائفة ، والاتصالات غير الضرورية لنا ، وضعف العلامات ، وأوجه القصور الأخرى.
في
المقالة الأولى ، نظرنا إلى الصور مع علامات الحذف والضوضاء ، وسوف نستمر في دراستها. تتمثل ميزة هذا النهج في أنه إذا وجدت أي ميزة جذابة لشبكة مدربة على مجموعة صور تعسفية ، فليس من الواضح ما إذا كانت هذه خاصية شبكة أم خاصية مجموعة تدريب. المعلمات الإحصائية للتسلسل مأخوذة من العالم الحقيقي غير معروفة. في الآونة الأخيرة ، تحدث Grandmaster Pleskov Pavel
paske57 عن مدى سهولة أحيانًا الفوز بتصنيف تجزئة / تصنيف للصور إذا كان من الجيد الخوض في البيانات بنفسك ، على سبيل المثال ، راجع البيانات الوصفية للصور. وليس هناك ما يضمن أنه في البيانات الحقيقية لا توجد مثل هذه التبعيات ، تُرك بلا إراد. لذلك ، لدراسة خصائص الشبكة ، نلتقط صوراً ذات علامات اهليلجيه ومستطيلات ، ونحدد المكان واللون والمعلمات الأخرى باستخدام مولد الأرقام العشوائية لجهاز الكمبيوتر (الذي لديه مولد عشوائي زائف ، وله مولد على أساس خوارزميات غير رقمية وخواص فيزيائية للمادة ، لكننا لن نناقش هذا في هذه المقالة).
لذا ، خذ البحر
np.random.sample () * 0.75 ، لسنا بحاجة إلى الأمواج والرياح والسواحل والأنماط والوجوه الخفية الأخرى. سيتم أيضًا رسم السفن / القطع الناقصة بنفس اللون ، ولتمييز البحر عن القارب والتداخل ، أضف 0.25 إلى البحر أو القارب / التشويش ، وستكون جميعها بنفس الشكل - علامات بيضاوية ذات أحجام واتجاهات مختلفة. سيكون التداخل أيضًا مستطيلات فقط من نفس لون القطع الناقص - وهذا أمر مهم ، المعلومات والتداخل من نفس اللون على خلفية الضوضاء. سنقوم فقط بإجراء تغيير بسيط على التلوين وسنقوم بتشغيل
np.random.sample () لكل صورة ولكل قطع ناقص / مستطيل ، أي لا تتكرر الخلفية ولا لون القطع الناقص / المستطيل. علاوة على ذلك ، يوجد نص في البرنامج لإنشاء صور / أقنعة ومثال على عشرة أزواج تم اختيارها عشوائيا.
استخدم إصدارًا شائعًا جدًا من الشبكة (يمكنك أن تأخذ شبكتك المفضلة) وحاول تحديد وإظهار التكرار لسلسلة تدريب كبيرة ، للحصول على نوع من الخصائص النوعية والكمية على الأقل للتكرار. أي يعتقد المؤلف أن العديد من غيغا بايت من تسلسل التدريب هي زائدة عن الحاجة إلى حد كبير ، وهناك العديد من الصور غير الضرورية ، ليست هناك حاجة لتحميل العشرات من وحدات معالجة الرسومات والقيام بعمليات حسابية غير ضرورية. يتجلى التكرار للبيانات ليس فقط وليس في حقيقة أن الأجزاء نفسها يتم عرضها في صور مختلفة ، ولكن أيضًا في التكرار للمعلومات في هذه البيانات. قد تكون البيانات زائدة عن الحاجة حتى إذا لم يتم تكرارها بالضبط. يرجى ملاحظة أن هذا ليس تعريفًا صارمًا للمعلومات وكفايتها أو التكرار. نريد فقط معرفة مقدار ما يمكنك تقليل القطار ، وما هي الصور التي يمكنك إزالتها من التسلسل التدريبي ، وعدد الصور التي تكفي للتدريب (سنضع الدقة في أنفسنا في البرنامج). هذا برنامج محدد ، ومجموعة بيانات محددة ، ومن الممكن ألا يعمل أي شيء على القطع الناقصة ذات المثلثات ، مثل العائق ، وكذلك على علامات القطع المستطيلة (فرضيتي هي أن كل شيء سيكون هو نفسه ، لكننا لا نتحقق منه الآن. ، نحن لا نجري التحليل ولا نثبت النظريات).
لذلك ، أعطيت:
- تعلم تسلسل صورة / قناع أزواج. يمكننا توليد أي عدد من أزواج الصور / الأقنعة. سأجيب عن السؤال على الفور - لماذا يكون اللون والخلفية عشوائيًا؟ سأجيب ببساطة ، باختصار ، بشكل واضح وشامل لأني أحب ذلك كثيرًا ، ليست هناك حاجة إلى كيان إضافي في شكل حد ؛
- الشبكة عادية وعادية U-net ، معدلة قليلاً وتستخدم على نطاق واسع للتجزئة.
فكرة الاختبار:
- في التسلسل الذي تم إنشاؤه ، كما هو الحال في المهام الحقيقية ، يتم استخدام غيغابايت من البيانات. يعتقد المؤلف أن حجم التسلسل التدريبي ليس بالغ الأهمية ويجب ألا يكون هناك الكثير من البيانات ، لكن يجب أن يحتوي على "الكثير" من المعلومات. مثل هذا المبلغ ، عشرة آلاف زوج من الصور / الأقنعة ، ليس ضروريًا وستتعلم الشبكة من كمية أقل بكثير من البيانات.
لنبدأ ، حدد 10000 زوجًا ونفكر فيها بعناية. سنضغط كل الماء ، كل البتات غير الضرورية من تسلسل التدريب هذا ونستخدم كل البقايا الجافة موضع التنفيذ.
يمكنك الآن التحقق من الحدس الخاص بك وافتراض عدد الأزواج من كل 10000 يكفي لتدريب وتنبؤ آخر ، ولكن أيضًا إنشاء تسلسل من 10000 زوج بدقة أكثر من 0.98. اكتب على قطعة من الورق ، بعد المقارنة.
للاستخدام العملي ، يرجى مراعاة أن كل من البحر والسفن التي تتداخل قد تم اختيارها بشكل مصطنع ، وهذا هو
np.random.sample () .
نقوم بتحميل المكتبات ، ونحدد أحجام مجموعة من الصورimport numpy as np import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.optimizers import Adam from keras.layers import Input,Conv2D,Conv2DTranspose,MaxPooling2D,concatenate from keras.layers import BatchNormalization,Activation,Add,Dropout from keras.losses import binary_crossentropy from keras import backend as K import tensorflow as tf import keras as keras w_size = 128 train_num = 10000 radius_min = 10 radius_max = 20
تحديد وظائف الخسارة والدقة def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
سوف نستخدم المقياس من
المقال الأول . دعني أذكّر القراء بأننا سنتنبأ بقناع البيكسل - هذا هو "البحر" أو "السفينة" وتقييم حقيقة أو زيف التنبؤ. أي الخيارات الأربعة التالية ممكنة - لقد توقعنا بشكل صحيح أن البيكسل هو "بحر" ، وتوقعنا بشكل صحيح أن البيكسل هي "سفينة" أو أخطأ في توقع "بحر" أو "سفينة". وهكذا ، بالنسبة لجميع الصور وجميع وحدات البكسل ، نقدر عدد الخيارات الأربعة ونحسب النتيجة - سيكون ذلك نتيجة الشبكة. وكلما كانت التنبؤات أقل خطأ والأكثر صحة ، كانت النتيجة أكثر دقة وأفضل شبكة.
ولأغراض البحث ، لنأخذ خيار شبكة U-net المدروسة جيدًا ، وهي شبكة ممتازة لتجزئة الصور. تم اختيار خيار U-net غير الكلاسيكي ، لكن الفكرة هي نفسها ، حيث تقوم الشبكة بعملية بسيطة للغاية مع الصور - فهي تقلل بعد الصورة مع بعض التحويلات خطوة بخطوة ثم تحاول استعادة القناع من الصورة المضغوطة. أي يتم رفع بُعد الصورة في حالتنا إلى 16 × 16 ، ثم نحاول استعادة القناع باستخدام بيانات من جميع طبقات الضغط السابقة.
نحن نفحص الشبكة على أنها "صندوق أسود" ، ولن ننظر إلى ما يحدث مع الشبكة في الداخل ، وكيف تتغير الأوزان وكيف يتم اختيار التدرجات - هذا هو موضوع دراسة أخرى.
U- صافي مع كتل def convolution_block(x, filters, size, strides=(1,1), padding='same', activation=True): x = Conv2D(filters, size, strides=strides, padding=padding)(x) x = BatchNormalization()(x) if activation == True: x = Activation('relu')(x) return x def residual_block(blockInput, num_filters=16): x = Activation('relu')(blockInput) x = BatchNormalization()(x) x = convolution_block(x, num_filters, (3,3) ) x = convolution_block(x, num_filters, (3,3), activation=False) x = Add()([x, blockInput]) return x
وظيفة توليد أزواج الصور / القناع. على صورة ملونة 128 × 128 مملوءة بالضوضاء العشوائية مع اختيار عشوائي من نطاقين ، إما 0.0 ... 0.75 أو 0.25..1.0. ضع علامة القطع بطريقة عشوائية عشوائياً في الصورة ثم ضع مستطيلًا في نفس المكان. نتحقق من أنها لا تتقاطع ، وإذا لزم الأمر ، قم بتحويل المستطيل إلى الجانب. في كل مرة نقوم بإعادة حساب قيم تلوين البحر / القارب. للبساطة ، سنضع القناع مع الصورة في صفيف واحد ، مثل اللون الرابع ، أي Red.Green.Blue.Mask ، إنه أسهل.
def next_pair(): img_l = (np.random.sample((w_size, w_size, 3))* 0.75).astype('float32') img_h = (np.random.sample((w_size, w_size, 3))* 0.75 + 0.25).astype('float32') img = np.zeros((w_size, w_size, 4), dtype='float') p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p1 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p2 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p3 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) p4 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) poly = np.array(( (p1, p2), (p1, p2+p4), (p1+p3, p2+p4), (p1+p3, p2), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc_rr = list(set(rr) & set(rr_p)) in_sc_cc = list(set(cc) & set(cc_p)) if len(in_sc_rr) > 0 and len(in_sc_cc) > 0: if len(in_sc_rr) > 0: _delta_rr = np.max(in_sc_rr) - np.min(in_sc_rr) + 1 if np.mean(rr_p) > np.mean(in_sc_rr): poly[:,0] += _delta_rr else: poly[:,0] -= _delta_rr if len(in_sc_cc) > 0: _delta_cc = np.max(in_sc_cc) - np.min(in_sc_cc) + 1 if np.mean(cc_p) > np.mean(in_sc_cc): poly[:,1] += _delta_cc else: poly[:,1] -= _delta_cc rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img[:,:,:3] = img_l.copy() img[rr, cc,:3] = img_h[rr, cc] img[rr_p, cc_p,:3] = img_h[rr_p, cc_p] else: img[:,:,:3] = img_h.copy() img[rr, cc,:3] = img_l[rr, cc] img[rr_p, cc_p,:3] = img_l[rr_p, cc_p] img[:,:,3] = 0. img[rr, cc,3] = 1. return img
لنقم بإنشاء تسلسل تدريب للأزواج ، انظر 10 عشوائي
_txy = [next_pair() for idx in range(train_num)] f_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) f_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy)
الخطوة الأولى دعونا نحاول تدريب على مجموعة الحد الأدنى
الخطوة الأولى من تجربتنا بسيطة ، فنحن نحاول تدريب الشبكة على التنبؤ بـ 11 صورة فقط.
batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f_imgs[m0_select>0], f_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0666 : : 47it [00:29, 5.82it/s]اخترنا أول 11 من التسلسل الأولي وتدريبهم على الشبكة. الآن لا يهم ما إذا كانت الشبكة تحفظ هذه الصور على وجه التحديد أو تلخصها ، الشيء الرئيسي هو أنها تستطيع التعرف على هذه الصور الأحد عشر حسب حاجتنا. اعتمادًا على مجموعة البيانات والدقة المحددة ، يمكن أن يستمر التدريب على الشبكة لفترة طويلة جدًا. ولكن لدينا فقط عدد قليل من التكرار. وأكرر أنه ليس من المهم بالنسبة لنا الآن كيف وما تعلمته الشبكة أو تعلمتها ، والشيء الرئيسي هو أنها وصلت إلى الدقة المحددة للتنبؤ.
الآن ابدأ التجربة الرئيسية
سنأخذ أزواج جديدة من الصور / القناع من التسلسل الذي تم إنشاؤه وسنحاول التنبؤ بها بواسطة الشبكة المدربة على التسلسل المحدد بالفعل. في البداية ، يوجد 11 زوجًا فقط من الصورة / القناع ويتم تدريب الشبكة ، وربما ليس بشكل صحيح. إذا كان القناع من الصورة في زوج جديد يتم التنبؤ به بدقة مقبولة ، فإننا نتجاهل هذا الزوج ، ولا يحتوي على معلومات جديدة للشبكة ، فهو يعرف بالفعل القناع ويمكنه حسابه من هذه الصورة. إذا كانت دقة التنبؤ غير كافية ، فإننا نضيف هذه الصورة بقناع إلى تسلسلنا ونبدأ في تدريب الشبكة حتى يتم التوصل إلى نتيجة دقة مقبولة على التسلسل المحدد. أي تحتوي هذه الصورة على معلومات جديدة وقمنا بإضافتها إلى تسلسل التدريب الخاص بنا واستخراج المعلومات الموجودة فيها عن طريق التدريب.
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9830 loss 0.0287 selected img 271 tested img 9949 : : 1563it [14:16, 1.01it/s]
يتم استخدام الدقة هنا بمعنى "الدقة" ، وليس كمقياس keras قياسي ، ويتم استخدام الروتين الفرعي "my_iou_metric" لحساب الدقة. من المثير للاهتمام مراقبة دقة وعدد الصور التي تم التحقيق فيها والإضافة إليها. في البداية ، تتم إضافة جميع أزواج الصور / القناع تقريبًا بواسطة الشبكة ، وفي مكان ما حوالي 70 يبدأ في التخلص منها. أقرب إلى 8000 يلقي جميع الأزواج تقريبا.
تحقق من الأزواج العشوائية المرئية التي حددتها الشبكة:
fig, axes = plt.subplots(2, 10, figsize=(20, 5)) t_imgs = f_imgs[m0_select>0] t_msks = f_msks[m0_select>0] for k in range(10): kk = np.random.randint(t_msks.shape[0]) axes[0,k].set_axis_off() axes[0,k].imshow(t_imgs[kk]) axes[1,k].set_axis_off() axes[1,k].imshow(t_msks[kk].squeeze())
لا شيء خاص أو خارق:
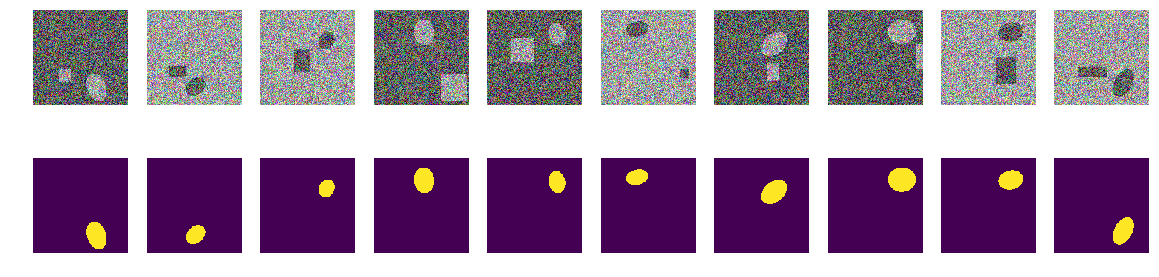
هذه هي أزواج مختارة من قبل الشبكة في مراحل مختلفة من التدريب. عندما تتلقى الشبكة زوج إدخال من هذا التسلسل ، لم تتمكن من حساب القناع بدقة محددة وتم تضمين هذا الزوج في تسلسل التدريب. ولكن لا شيء خاص ، صور عادية.
التحقق من النتيجة والدقة
دعونا نتحقق من جودة برنامج التدريب على الشبكة ، وتأكد من أن الجودة لا تعتمد بشكل كبير على ترتيب التسلسل الأولي ، الذي نمزج معه التسلسل الأولي لأزواج الصورة / القناع ، ونأخذ 11 الأخرى أولاً وبنفس الطريقة ، وقم بتدريب الشبكة ونقطع الفائض.
sh = np.arange(train_num) np.random.shuffle(sh) f0_imgs = f_imgs[sh] f0_msks = f_msks[sh] model.compile(loss=bce_dice_loss, optimizer="adam", metrics=[my_iou_metric]) model.summary()
كود تجريب batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f0_imgs[m0_select>0], f0_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0710 : : 249it [01:03, 5.90it/s]
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9890 loss 0.0224 selected img 408 tested img 9456 : : 1061it [21:13, 2.16s/it]
لا تعتمد النتيجة بشكل كبير على ترتيب أزواج التسلسل الأصلي. في الحالة السابقة ، اخترت الشبكة 271 ، الآن 408 ، إذا قمت بخلطها ، يمكن أن تختار الشبكة مبلغًا مختلفًا. لن نفحص ، يعتقد المؤلف أنه سيكون هناك دائمًا أقل من 10000 دائمًا.
تحقق من دقة التنبؤ بالشبكة في تسلسل مستقل جديد
_txy = [next_pair() for idx in range(train_num)] test_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) test_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy) test_pred_0 = model.predict(test_imgs) t_val_0 = get_iou_vector(test_msks,test_pred_0) t_val_0
0.9927799999999938
الملخص والاستنتاجات
لذلك ، تمكنا من الضغط من أقل من ثلاث أو أربعمائة تم اختيارها من بين 10000 زوج ، ودقة التنبؤ هي 0.99278 ، وأخذنا جميع الأزواج التي تحتوي على بعض المعلومات المفيدة على الأقل وطردنا الباقي. لم نقم بمحاذاة المعايير الإحصائية للتسلسل التدريبي ، ولم نقم بإضافة تكرار المعلومات ، إلخ. ولم تستخدم الأساليب الإحصائية على الإطلاق. نلتقط صورة تحتوي على معلومات لا تزال غير معروفة للشبكة ونضغط كل شيء منها في ثقل الشبكة. إذا كانت الشبكة تقابل صورة "غامضة" واحدة على الأقل ، فستستخدمها كلها في الأعمال التجارية.
يحتوي ما مجموعه 271 زوجًا من أزواج الصور / القناع على معلومات للتنبؤ بـ 10000 زوج مع دقة لا تقل عن 0.8075 لكل زوج ، أي أن الدقة الكلية على التسلسل بأكمله أعلى ، لكن في كل صورة لا يقل عن 0.8075 ، ليس لدينا صور لا نملكها يمكننا التنبؤ ونعرف الحدود الدنيا لهذا التوقع. (هنا ، بالطبع ، تفاخر المؤلف ، كيف بدون هذا ، لا يتحقق المقال من هذا البيان ، حوالي 0.8075 ، أو دليل ، لكن على الأرجح هذا صحيح)
لتدريب الشبكة ، ليست هناك حاجة لتحميل وحدة معالجة الرسومات (GPU) بكل ما يمكن توفيره ، يمكنك سحب قلب القطار وتدريب الشبكة عليه كبداية للتدريب. عند حصولك على صور جديدة ، يمكنك تحديد تلك التي لا تستطيع الشبكة التنبؤ بها وإضافتها إلى جوهر القطار يدويًا ، وإعادة تدريب الشبكة مرة أخرى للضغط على جميع المعلومات من الصور الجديدة. وليس من الضروري تحديد تسلسل التحقق من الصحة ؛ يمكننا أن نفترض أن كل شيء آخر ، ما عدا المحدد ، هو تسلسل تحقق.
واحد أكثر رياضيا ليست صارمة ، ولكن ملاحظة مهمة للغاية. من الآمن القول أن كل زوج من صور / قناع يحتوي على "الكثير" من المعلومات. يحتوي كل زوج على "الكثير" من المعلومات ، رغم أن المعلومات تتقاطع أو تتكرر في معظم أزواج الصور / القناع. يحتوي كل زوج من أزواج الصور / القناع البالغ عددها 271 على معلومات ضرورية للتنبؤ ، ولا يمكن ببساطة التخلص من هذا الزوج.
حسنًا ، هناك ملاحظة صغيرة حول الطيات ، حيث يقسم العديد من الخبراء وكاجلر التسلسل التدريبي إلى طيات ويقومون بتدريبهم بشكل منفصل ، ويجمعون بين النتائج التي يتم الحصول عليها بطرق أكثر صعوبة. في حالتنا ، يمكنك أيضًا تقسيمها إلى ثنيات ، إذا قمت بإزالة 271 زوجًا من 10000 ، فيمكنك إنشاء تسلسل جذر جديد في الباقي ، مما سيؤدي بوضوح إلى توفير نتيجة مختلفة ولكن قابلة للمقارنة. يمكنك ببساطة مزج الـ 11 الأولية الأخرى ، كما هو موضح أعلاه.
توفر المقالة رمزًا وتوضح كيفية تدريب U-net لتجزئة الصور. هذا مثال ملموس ، وفي المقالة ، لا توجد تعميمات على الشبكات الأخرى ، إلى تسلسلات أخرى ، لا توجد رياضيات صارمة ، كل شيء يُقال ويظهر "على الأصابع". مجرد مثال لكيفية تعلم الشبكة مع تحقيق دقة مقبولة.