لقد وجدت هذا النمط عندما نظرت إلى وظيفة المستخدم
xcont . بعد أن عثرت على
هذا المنشور ، لفتت الانتباه إلى حقيقة أن الأنماط تتكرر ليس فقط مع زيادة الحجم وفقًا لأرقام فيبوناتشي.

كنت أتساءل ما إذا كان هناك نمط في هذه الأنماط. لكن مع وجود معلمتين فقط
x و
y ، قررت أنني بحاجة إلى تعيين شيء آخر ، مشترك بين جميع الأنماط التي تم الحصول عليها. ثم لاحظت أننا إذا أخذنا المربعات الأربعة الأولى في الحقل ، فسنحصل على أي حال على 3 خيارات لبداية النموذج ، إذا كان الخط يسير:
أعلى (↑)

أسفل (↓)

أو لا تذهب * (-)

للتسمية ، قررت استخدام هذه الرموز ↑ ، ↓ ، واصفا إياها بشروط تدور (مثل تدور الجسيمات). وهنا بدأت في إنشاء جدول من تبعيات هذه الدورات إلى
x ،
y .
أولاً ، دعنا نرى ما إذا كان هناك نمط إذا
تم تغيير
y ،
x ، خذ 4

والآن عن الخصائص
نرى سلسلة من الدورات
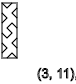
- ↑ - ↓ - ↑ - ↓ - ↑ - ↓يكرر النمط بتسلسل معين
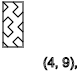
ذ = 3،7،11 ... (
↑ )
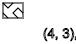
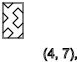
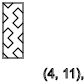
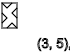
y = 5،9،13 ... (
↓ )
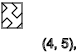
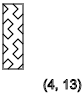
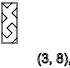
y = 2،4،6،8،10،12 ... (
- )
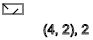
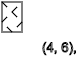
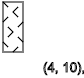
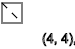
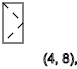
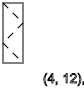
نحصل على نفس الشيء إذا كانت
x = 3 ، نرى سلسلة من الدورات
↑ - ↓ ↑ - ↓ ↑ - ↓ ↑ - ↓ ↑
ذ = 2،5،8،11 ... (
↑ )
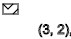
ذ = 4،7،10،13 ... (
↓ )

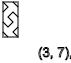
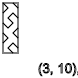
ذ = 3.6،9،12 ... (
- )
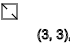
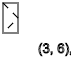
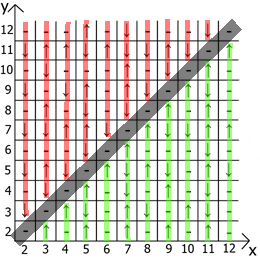
اعتقدت أنه يمكنني تنظيم هذه التسلسلات وتجميع جدول من هذه الدورات ، وهذا ما حصلت عليه.
أقدم لكم ، "الجدول الأسود".
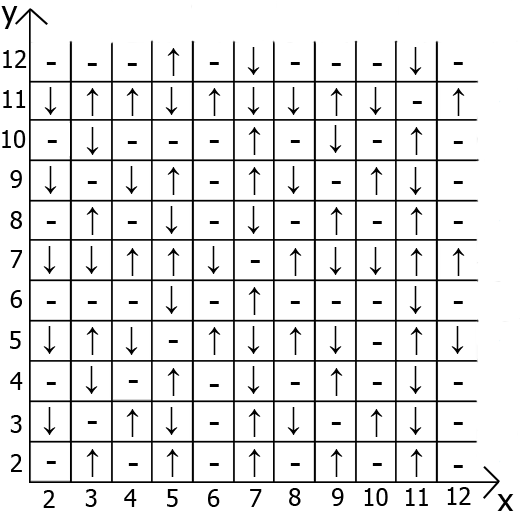
الشيء الأكثر إثارة للاهتمام هو أن هذا الجدول له التبعيات والخصائص.
أولاً ، نشتق بعض الصيغ:
→إذا كانت
x متساوية و
y تساوي → - ، أيضًا إذا كانت
x ⋮ y أو
y ⋮ x → -
س = ذ → -
x = y + 1 → ↑
س = ص -1 → ↓
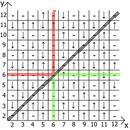
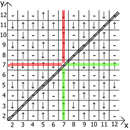
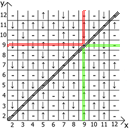
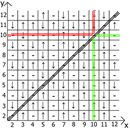
والآن حول خصائص الجدول نفسه ، إذا أخذنا x = y كنقطة مرجعية ، فعندئذٍ في أي اتجاه لدينا تسلسلات تعكس المرآة (يشار إليها بخطوط حمراء وخضراء).
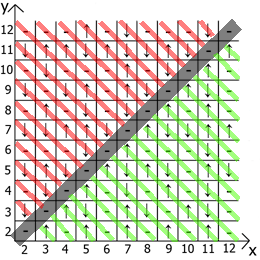
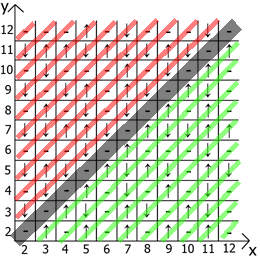
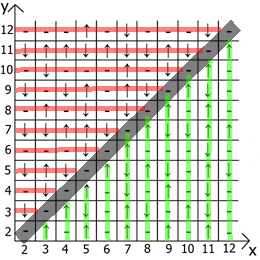
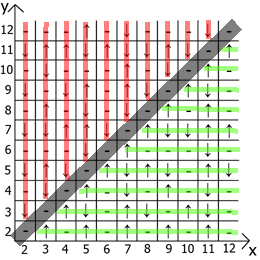
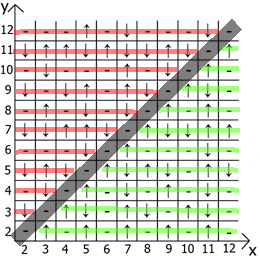

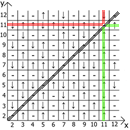
في الواقع تجد الاستخدام والاستخدام. لدي جدول يصل إلى 12 ، منذ البداية فعلت كل هذا على الورق.

ولكن باستخدام
خوارزمية جافا سكريبت JavaScript ، يمكنك أن تبحث عن قيم أكبر.
ملاحظة : لا أعرف كيف يمكن استخدام هذا ، ولكن ربما يمكن تطبيق هذه الخوارزمية على جهاز كمبيوتر الكم.
الروابط:
واحد واثنين .