اكتشف عالم الرياضيات الهواة أصغر تغطية عالمية

من خلال حسابات هندسية صعبة ، اكتشف Philip Gibbs أصغر طلاء معروف لأي شكل ممكن.

يمكن وصف غطاء عالمي مثل مسدس حول أي شكل.

فيليب جيبس ​​ليس عالم رياضيات محترف. لذلك ، عندما أراد التفكير في مهمة ، كان يبحث عن مهمة يمكن للهواة التعامل معها. اكتشف مهمة صعبة يمكن أن تدفع حتى أفضل العقول إلى الجنون. وفي مقالة نشرت هذا العام ، أحرز جيبز تقدماً ملحوظاً في حل مسألة قبل مائة عام ، اعتمادًا على القدرة على قياس المساحة بدقة حسب المقاييس الذرية.

أول من اقترح هذه المشكلة كان عالم الرياضيات الفرنسي هنري ليون ليبسجو ، في رسالة إلى صديقه يوليوس بال ، كتب في عام 1914. سأل Lebesgue: ما هو شكل أصغر مساحة ممكنة ، قادرة على تغطية عدد كبير من الأشكال الأخرى بالكامل (امتلاك خاصية مشتركة واحدة ، موصوفة أدناه)؟

خلال القرن الماضي ، تحولت مهمة العثور على غطاء عالمي إلى مصيدة فئران: كان التقدم المحرز في حلها ، إذا حدث بشكل دوري ، صغيرًا بشكل مثير للدهشة. أصبح تحسين Gibbs لهذا الأمر دراماتيكيًا - على الرغم من أنك لا تزال بحاجة إلى التفكير فيه قليلاً.

تخيل اثني عشر قصاصات من الورق بأحجام وأشكال مختلفة ملقاة على الأرضية. تخيل الآن أنك عرضت على تقديم شكل آخر كبير بما يكفي لتغطية أي من الأشكال المتاحة. من خلال التجريب - عن طريق تركيب النماذج وتحويلها - يمكنك الخروج بطريقة ما لحل هذه المشكلة. ولكن بعد أن وجدت تغطية شاملة ، هل يمكنك التأكد من أنك قد وجدت أصغرها؟ يمكنك أن تتخيل أنه خلال اليوم تعود بشكل دوري إلى النموذج الخاص بك ، وتجد الفرصة لقطع بعض القطع الإضافية هنا وهناك.

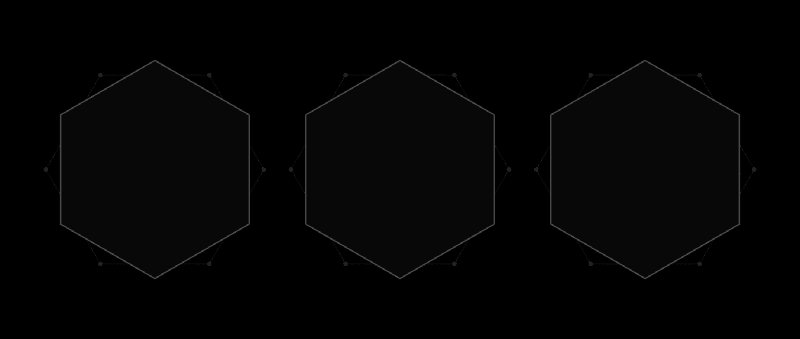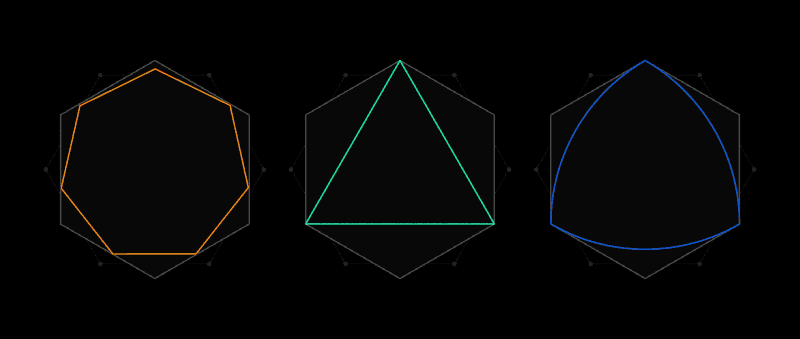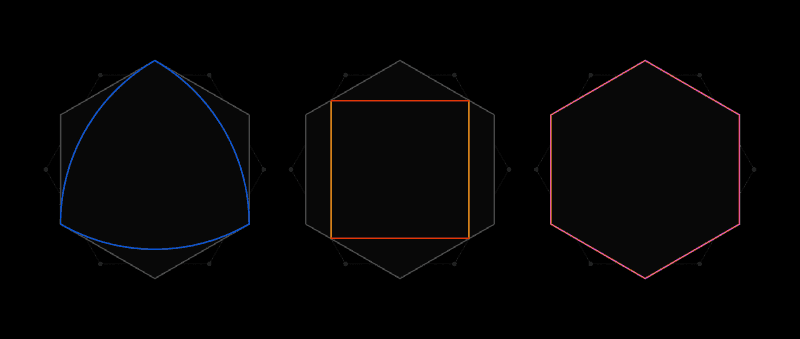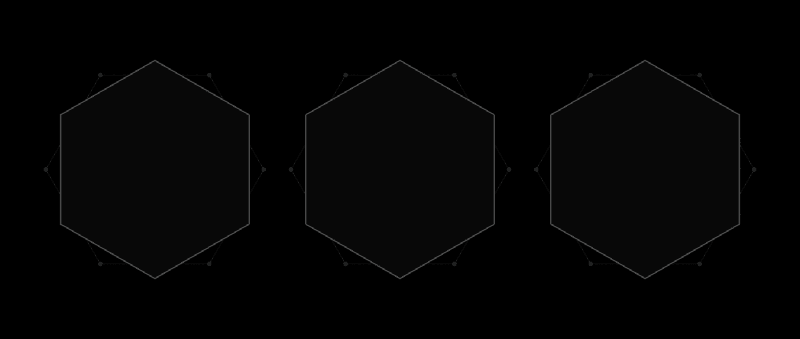
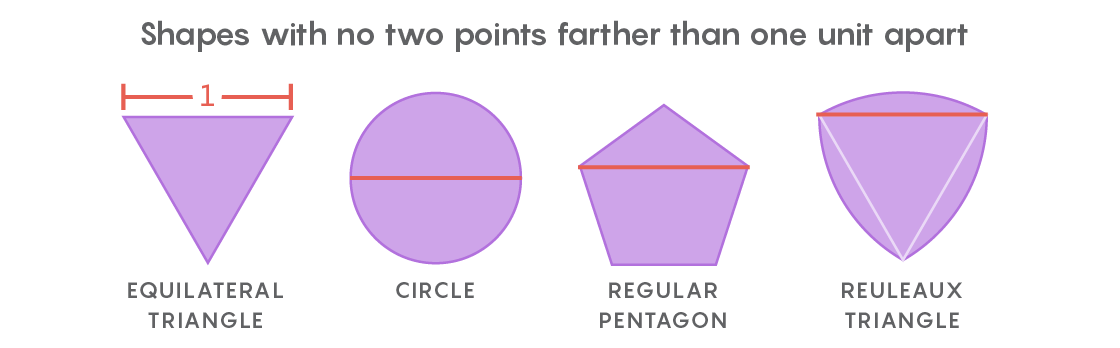
هذه هي روح مشكلة التغطية الشاملة من Lebesgue. بدلاً من قصاصات الورق ، فإنه يأخذ في الاعتبار الأشكال التي لا توجد فيها مسافات متباعدة بين وحدة طول متباعدة. سيكون الشكل الأكثر وضوحًا هو دائرة قطرها 1 ، ولكن يوجد عدد لا حصر له: مثلث متساوي الأضلاع ، خماسي منتظم ، مسدس منتظم ، شكل مثلث ذو جوانب منتفخة ، والمعروف باسم مثلث روهلو - وهذا فقط للمبتدئين. مجموعة متنوعة من الأشكال يجعل من الصعب العثور على أصغر غطاء لهم جميعا.



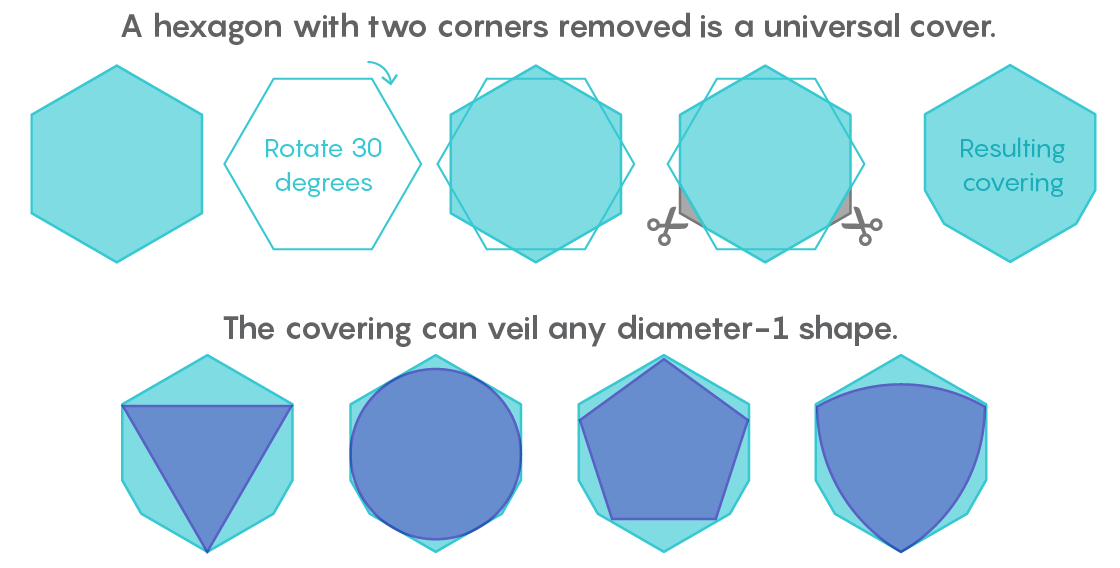
بعد وقت قصير من تلقي خطاب من Lebesgue ، أدركت Pal أن مسدس منتظم سيكون الغطاء العالمي. ثم قام بتحسين هذه النتيجة ، مشيرًا إلى أنه من خلال قطع زاويتين من المسدس ، وعدم الوقوف بجانب بعضهما البعض ، يمكنك الحصول على شكل بمساحة أصغر ، والذي لا يزال سيتحول إلى طبقة عالمية.

"خذ مسدسًا ، ثم ضع رأسًا ثانيًا فوقه ، وقلبه 30 درجة ، وقطع زاويتين. هذا هو المكان الذي أنهى فيه بال البحث "، قال جيبس.

في الثمانين عامًا التالية ، قام عالمان رياضيان آخران بفصل الأشرطة الضيقة عن غطاء Pal العالمي. في عام 1936 ، قام رولاند سبراج بإزالة قطعة صغيرة بجانب أحد الزوايا. في عام 1992 ، ستقوم Hansen بإزالة اثنين من الأوتاد المصغرة من الزوايا السفلية اليمنى واليسرى. يمكن أن تنقل الرسوم التوضيحية لهانسن موقع هذه الأجزاء ، ولكن ليس حجمها: كانت مساحتها 0.00000000004 وحدة.



وقال جون بايز ، عالم الرياضيات بجامعة كاليفورنيا في ريفرسايد: "لا يمكنك رسمها على مقياس ، وستكون بحجم ذرة".

أخرج بايز مهمة Lebesgue بدافع النسيان عندما كتب عنها في مدونته حول الرياضيات الشائعة في عام 2013. لقد اعترف بأنه كان مفتونًا بهذه المهمة بطريقة يمكن أن يثيرها لك مقطع فيديو به حشرة غارقة. "اهتمامي بالمهمة كان غير صحي" ، كتب بيز. "لا أعرف الأسباب التي تجعله مهمًا". لا أرى كيف يمكنه التواصل مع العديد من المهام الرائعة الأخرى. يبدو فقط معقدة بشكل لا يصدق مقارنة الانطباع الأول. أنا معجب بالأشخاص الذين يعملون عليها بقدر ما أعجب الناس الذين يقررون عبور القارة القطبية الجنوبية على الزلاجات ".

لم يعبر Philib Gibbs أبدًا القارة القطبية الجنوبية على الزلاجات ، ولكن اقرأ مدونة Baez. عندما التقى بسجل لمشكلة Lebesgue ، فكر: "حسنًا ، هذا هو بالضبط ما أحتاج إليه."

مقص ذري

اعتقد جيبز ذات مرة أنه يمكن أن يصبح عالما. حصل على دبلوم في الرياضيات من جامعة كامبريدج ودكتوراه في الفيزياء النظرية من جامعة غلاسكو. ومع ذلك ، فقد سرعان ما فقد حماسته للبحوث الأكاديمية وأصبح مبرمجًا. عمل على أنظمة تصميم السفن وإدارة الحركة الجوية والتمويل ، وفي عام 2006 تقاعد.

ظل جيبس ​​مهتمًا بالمسائل الأكاديمية ، لكن كباحث عادي ، لم يكن بإمكانه فعل الكثير. وقال: "من الصعب على عالم مستقل متابعة ما يحدث". "ولكن إذا وجدت المكان المناسب ، فيمكنك القيام بشيء ما والحصول على بعض النتائج المفيدة."


عالم الرياضيات الهواة فيليب جيبس

كان مثل هذا مكانة مشكلة التغطية الشاملة Lebesgue. لم تحظ هذه المهمة أبدًا باهتمام علماء الرياضيات ، لذا شك في أنه قادر على تحقيق بعض التقدم. أدرك جيبس ​​أيضًا أن خبرته في البرمجة قد تكون ميزة. وقال: "أبحث دائمًا عن المشكلات التي يمكن فيها استخدام أجهزة الكمبيوتر والرياضيات التجريبية".

في عام 2014 ، قام Gibbs بإجراء محاكاة كمبيوتر لـ 200 شكل عشوائي من القطر 1. من عمليات المحاكاة ، تبع ذلك أنه قد يكون قادرًا على قطع قطعة صغيرة من الزاوية العليا من أصغر غطاء سابق. لقد حول هذا الأمر إلى دليل على أن الطلاء الجديد سيعمل على جميع الأشكال الممكنة من القطر 1. أرسل جيبس ​​الدليل إلى Baez ، الذي ساعد مع Gibbs مع أحد تلامذته ، Gibbs على منح العمل أسلوبًا رياضيًا رسميًا.

نشر الثلاثة منهم أعمالهم على الإنترنت في فبراير 2015. قلل من مساحة أصغر تغطية عالمية ممكنة من 0.8441377 إلى 0.8441153 وحدة. كانت وفورات 0.0000224 وحدة ما يقرب من مليون مرة أكبر مما حققته هانسن في عام 1992.

كان جيبس ​​واثقًا من أنه قادر على تحسين النتيجة. في أحد الأعمال التي نُشرت في شهر أكتوبر ، قام بقطع جزء كبير نسبيًا آخر عن الطلاء العام ، ليصل مساحته إلى 0.84409359 وحدة.



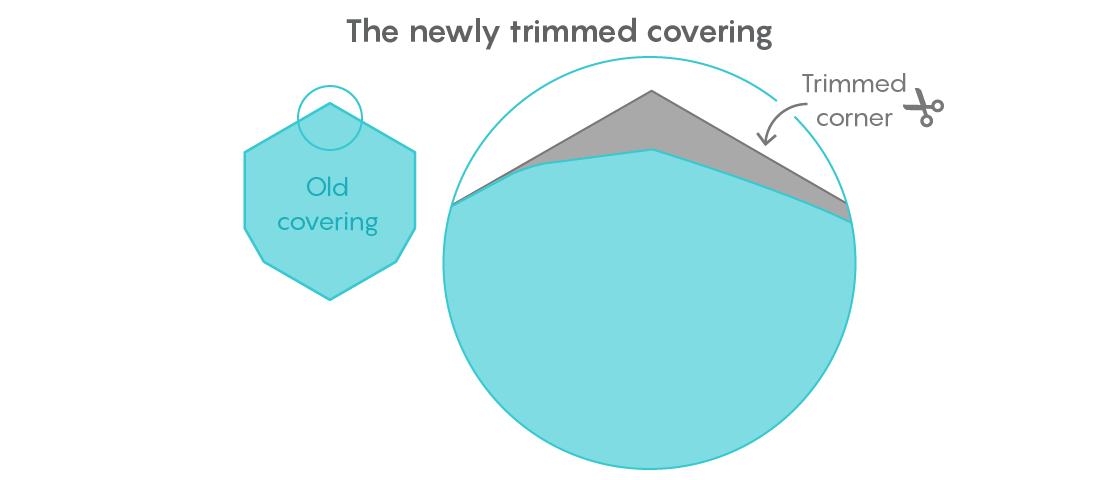
كانت استراتيجيته هي نقل جميع الأشكال التي يبلغ قطرها 1 إلى زاوية الطبقة العامة التي اكتشفها قبل عدة سنوات ، ثم إزالة المنطقة المتبقية بأكملها من الزاوية المقابلة. لكن القياس الدقيق للمساحة المحفوظة أثبت أنه صعب. استندت التقنيات المستخدمة من قبل جيبس ​​على الهندسة الإقليدية ، ولكن تم تنفيذها بدقة من شأنها أن تصدم أي طالب في المدرسة الثانوية.

"من وجهة نظر الرياضيات ، كل هذا هو الهندسة للمدرسة الثانوية. لكن تم تأديته بتوتر متعصب.

يحتل جيبس ​​حتى الآن المركز الأول بحثًا عن أصغر تغطية عالمية ، لكن جائزته في خطر. يعتقد جيبس ​​أن هناك فرصة للعثور على تغطية أصغر. يأمل بايز أن يحفز الاهتمام بعودة جيبس ​​إلى مشكلة Lebesgue اهتمام علماء الرياضيات الآخرين. ربما حان الوقت لترك جانبا الحاكم والبوصلة واستخدام ترسانة كاملة من الرياضيات الحديثة.

وقال "من الممكن أن تستخدم الطريقة الصحيحة لحل هذا اللغز أفكارًا مختلفة تمامًا ، على الرغم من أنه ليس لدي أي فكرة عن الأفكار التي يمكن أن تكون هذه".