دقة العمق بوضوح

دقة العمق هي ألم في المؤخرة أن يواجه أي مبرمج رسومات عاجلاً أم آجلاً. تمت كتابة الكثير من المقالات والأعمال حول هذا الموضوع. وفي الألعاب والمحركات المختلفة ، وعلى الأنظمة الأساسية المختلفة ، يمكنك رؤية العديد من التنسيقات والإعدادات المختلفة لمخزن مؤقت للعمق .

يبدو أن تحويل العمق على وحدة معالجة الرسومات (GPU) غير واضح بسبب كيفية تفاعله مع منظور المنظور ، ولا توضح دراسة المعادلات الموقف. لفهم كيفية عمل هذا ، من المفيد رسم بعض الصور.



هذه المقالة مقسمة إلى 3 أجزاء:

1. سأحاول شرح الدافع وراء تحول العمق غير الخطي .
2. سأقدم العديد من الرسوم البيانية التي ستساعدك على فهم كيفية عمل تحويل العمق غير الخطي في مواقف مختلفة ، حدسيًا وبصريًا.
3. مناقشة للنتائج الرئيسية لـ Tightening the Precision of Perspective Rendering [Paul Upchurch، Mathieu Desbrun (2012)] بشأن تأثير أخطاء الفاصلة العائمة الدائرية على دقة العمق.

لماذا 1 / ض؟

عادةً لا يقوم المخزن المؤقت لعمق وحدة معالجة الرسومات بتخزين تمثيل خطي للمسافة بين الكائن والكاميرا ، على عكس ما يتوقع بسذاجة أن يكون من الاجتماع الأول. بدلاً من ذلك ، يقوم المخزن المؤقت العمق بتخزين القيم بما يتناسب عكسياً مع عمق مساحة العرض. أريد أن أصف باختصار الدافع لمثل هذا القرار.

في هذه المقالة ، سأستخدم d لتمثيل القيم المخزنة في المخزن المؤقت للعمق (في النطاق [0 ، 1] لـ DirectX) ، و z لتمثيل مساحة عرض العمق ، أي المسافة الفعلية من الكاميرا ، في وحدات العالم ، على سبيل المثال متر. بشكل عام ، العلاقة بينهما لها الشكل التالي:



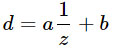
حيث a، b هي الثوابت المرتبطة بالإعدادات القريبة والبعيدة للطائرات. بمعنى آخر ، d هي دائمًا بعض التحولات الخطية من 1 / z .

للوهلة الأولى ، قد يبدو أن أي وظيفة لـ z يمكن اعتبارها d . إذن لماذا تبدو بهذه الطريقة؟ هناك سببان رئيسيان لذلك.

أولاً ، 1 / z يناسب بشكل طبيعي الإسقاط المنظور. وهذه هي أبسط أنواع التحولات ، والتي تضمن الحفاظ على الخطوط المستقيمة. لذلك ، فإن إسقاط المنظور مناسب لتنقيط الأجهزة ، حيث تظل الحواف المستقيمة للمثلثات مستقيمة على الشاشة. يمكننا الحصول على تحويل خطي من 1 / z ، مع الاستفادة من قسم المنظور الذي يؤديه GPU بالفعل:



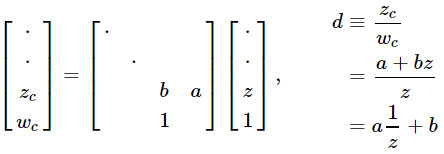
بطبيعة الحال ، تتمثل القوة الحقيقية لهذا النهج في أنه يمكن ضرب مصفوفة الإسقاط بمصفوفات أخرى ، مما يتيح لك دمج العديد من التحولات في واحدة.

السبب الثاني هو أن 1 / z خطي في مساحة الشاشة ، كما لاحظ إميل بيرسون . هذا يجعل من السهل استيفاء d في المثلث أثناء التنقيط ، وأشياء مثل المخازن المؤقتة للتسلسل الهرمي Z ، والتخزين المؤقت Z المبكر ، وعمق ضغط الضغط .

الرسوم البيانية العمق

المعادلات معقدة ، دعنا ننظر إلى بضع صور!



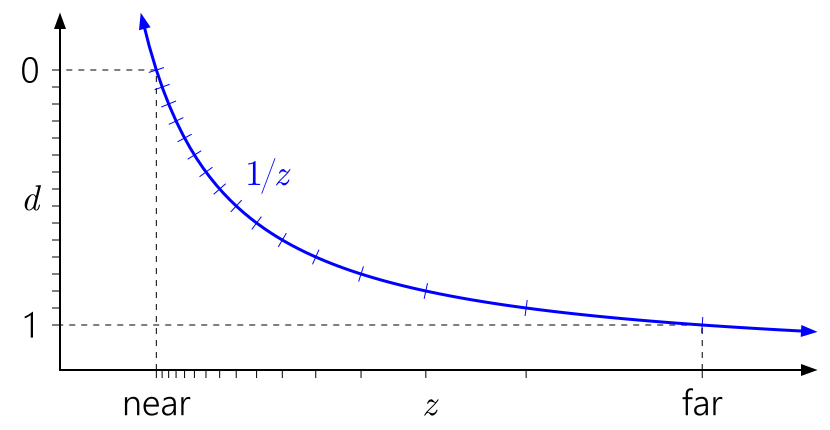
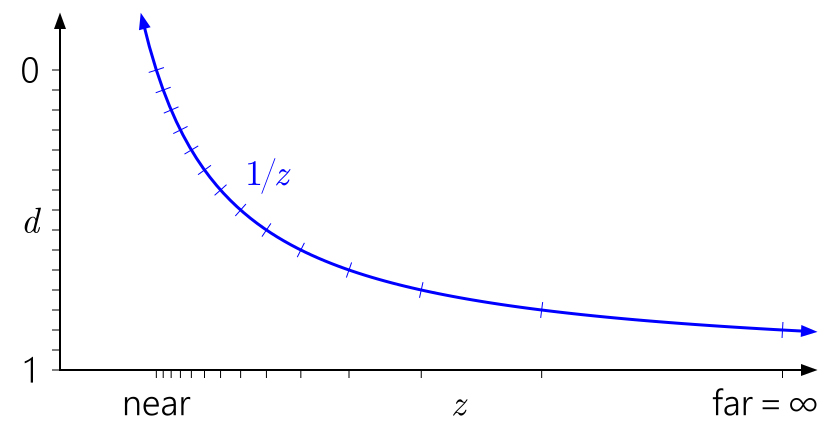
طريقة قراءة هذه المخططات هي من اليسار إلى اليمين ، ثم إلى الأسفل. ابدأ بـ d على المحور الأيسر. نظرًا لأن d يمكن أن يكون تحولًا خطيًا تعسفيًا من 1 / z ، فيمكننا ترتيب 0 و 1 في أي مكان مناسب على المحور. تشير العلامات إلى اختلاف قيم المخزن المؤقت للعمق . ولأغراض الوضوح ، أقوم بتصميم مخزن مؤقت بعمق صحيح مكون من 4 بت ، لذلك هناك 16 علامة متباعدة بشكل متساوٍ.

يوضح الرسم البياني أعلاه تحويل عمق الفانيليا "القياسي" إلى D3D وواجهات برمجة التطبيقات المماثلة. يمكنك أن تلاحظ على الفور كيف يتم تجميع القيم القريبة من المستوى القريب ، بسبب منحنى 1 / z ، والقيم القريبة من المستوى البعيد مبعثرة.

من السهل أيضًا فهم سبب تأثير قرب مستوى الطائرة على دقة العمق كثيرًا. ستؤدي المسافة القريبة من الطائرة إلى زيادة سريعة في قيم d بالنسبة إلى قيم z ، مما سيؤدي إلى توزيع غير متساوٍ للقيم:



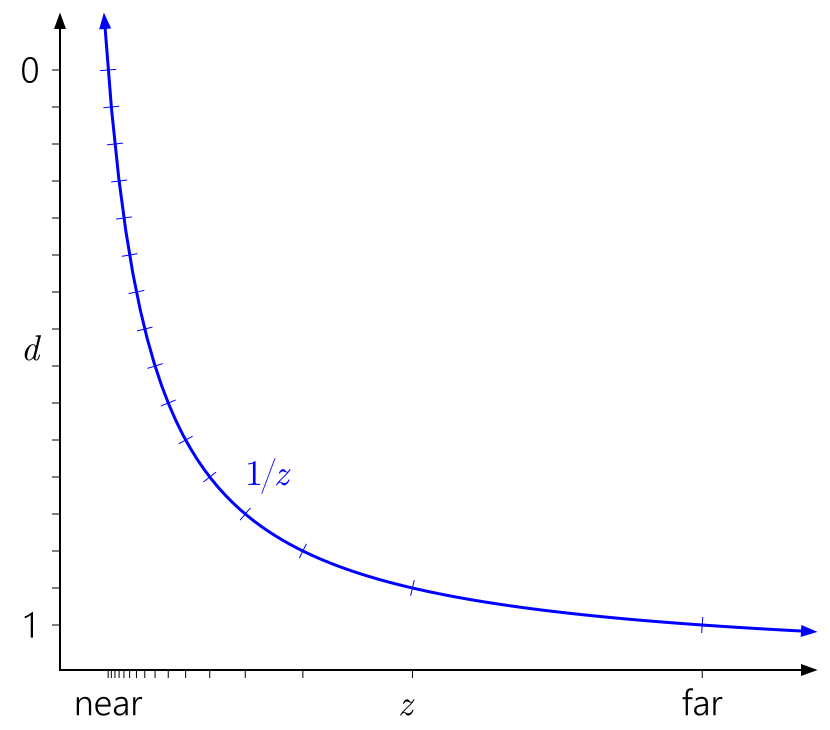
وبالمثل ، في هذا السياق ، من السهل معرفة السبب في أن تحريك الطائرة البعيدة إلى ما لا نهاية ليس له مثل هذا التأثير الكبير. هذا يعني فقط توسيع نطاق d إلى 1 / z = 0 :



ولكن ماذا عن عمق الفاصلة العائمة؟ تم إضافة الرسم البياني التالي علامات المطابقة للتنسيق العائم مع 3 بتات من الأس و 3 بتات من السرعوف:



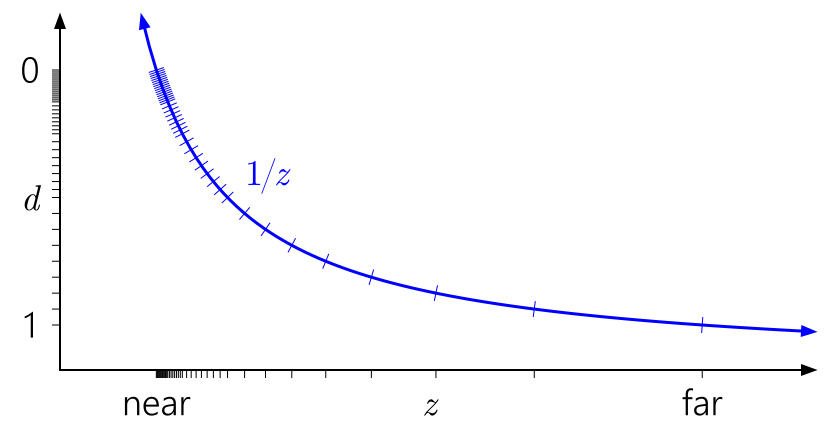
يوجد الآن في النطاق [0،1] 40 قيمة مختلفة - أكثر بقليل من 16 قيمة في وقت سابق ، لكن معظمها تم تجميعه بطريقة غير مجدية بالقرب من المستوى القريب (أقرب إلى 0 العوامة لها دقة أعلى) ، حيث لا نحتاج حقًا إلى دقة كبيرة.

حيلة مشهورة الآن هي عكس العمق ، وعرض الطائرة القريبة على d = 1 والطائرة البعيدة على d = 0 :



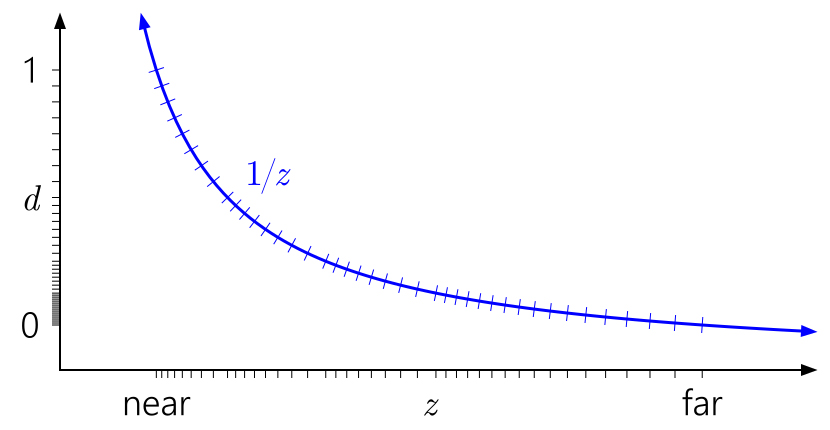
أفضل بكثير! والآن يعوض التوزيع شبه اللوغاريتمي للطفو بطريقة ما عن عدم الخطية لـ 1 / z ، بينما أقرب إلى المستوى القريب فإنه يعطي دقة تشبه المخزن المؤقت لعمق صحيح ، ويعطي دقة أكبر بكثير في مكان آخر. تتعمق دقة العمق ببطء شديد إذا تحركت بعيدًا عن الكاميرا.

ربما تم اختراع الخدعة العكسية- Z بشكل مستقل عدة مرات ، ولكن على الأقل ذكر أول مرة في ورقة SIGGRAPH '99 [Eugene Lapidous و Guofang Jiao (للأسف غير متاح للجمهور)]. ومؤخراً ، تم ذكره مجددًا على المدونة بواسطة مات بيتينو وبرانو كيمن ، وفي خطاب ألقاه إميل بيرسون وهو يصنع لعبة VAG Game Worlds SIGGRAPH 2012.

افترضت جميع الرسوم البيانية السابقة نطاقًا من العمق [0.1] بعد الإسقاط ، وهو اصطلاح في D3D. ماذا عن برنامج OpenGL ؟



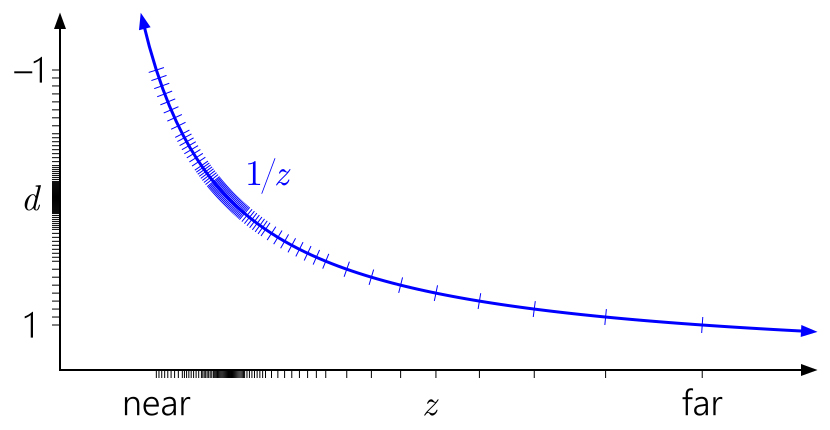
يفترض OpenGL افتراضيًا مجموعة من العمق [-1 ، 1] بعد الإسقاط. بالنسبة إلى التنسيقات الصحيحة ، لا يتغير أي شيء ، ولكن بالنسبة للفاصلة العائمة ، تتركز الدقة الكاملة في المنتصف. (يتم تعيين قيمة العمق إلى النطاق [0،1] للتخزين اللاحق في المخزن المؤقت للعمق ، لكن هذا لا يساعد ، حيث إن التعيين الأولي لـ [-1،1] دمر بالفعل كل الدقة في النصف الأقصى من النطاق.) وبسبب التناظر ، خدعة سوف عكس Z لا يعمل هنا.

لحسن الحظ ، في OpenGL لسطح المكتب ، يمكن إصلاح ذلك باستخدام الامتداد المدعوم على نطاق واسع ARB_clip_control (يبدأ أيضًا بـ OpenGL 4.5 ، glClipControl هو المعيار ). لسوء الحظ ، GL ES في الرحلة.

تأثير تقريب الأخطاء

يعد تحويل 1 / z واختيار عائم عمق int العائم جزءًا كبيرًا من قصة الدقة ، ولكن ليس كلها. حتى إذا كان لديك دقة عمق كافية لتمثيل المشهد الذي تحاول تقديمه ، فمن السهل أن تقوم بتقليل الدقة بأخطاء حسابية أثناء عملية تحويل الرأس.

في بداية المقال ، ذكر أن Upchurch و Desbrun درسوا هذه المشكلة. اقترحوا توصيتين رئيسيتين لتقليل أخطاء التقريب:

1. استخدام لانهائي طائرة بعيدة.
2. حافظ على مصفوفة الإسقاط منفصلة عن المصفوفات الأخرى ، وتطبيقها كعملية منفصلة في تظليل قمة الرأس ، بدلاً من دمجها مع مصفوفة العرض.

قدمت Upchurch و Desbrun هذه التوصيات باستخدام طريقة تحليلية تعتمد على معالجة أخطاء التقريب كأخطاء عشوائية صغيرة يتم تقديمها في كل عملية حسابية وتتبعها حسب الترتيب الأول في عملية التحويل. قررت اختبار النتائج في الممارسة العملية.

المصادر هنا هي بيثون 3.4 و numpy. يعمل البرنامج على النحو التالي: يتم إنشاء سلسلة من النقاط العشوائية ، مرتبة حسب العمق ، وتقع خطيا أو لوغاريتميا بين الطائرات القريبة والبعيدة. ثم يتم ضرب النقاط بواسطة عرض وإسقاط المصفوفة وتقسيم المنظور ، باستخدام تعويم 32 بت ، ويتم اختيارياً تحويل النتيجة النهائية إلى 24 بت. في النهاية ، يمر عبر التسلسل ويحسب عدد المرات التي أصبحت فيها نقطتان متجاورتان (كان لهما في البداية أعماق مختلفة) إما متطابقة ، حيث كان لهما نفس العمق أو تم تغيير الترتيب على الإطلاق. بمعنى آخر ، يقيس البرنامج التكرار الذي تحدث به أخطاء المقارنة العميقة - والتي تتوافق مع مشاكل مثل Z-fight - في سيناريوهات مختلفة.

فيما يلي النتائج لـ near = 0.1 ، أقصى = 10K ، بعمق خطي 10K. (جربت الفاصل الزمني لوغاريتمي العمق ونسب أخرى قريبة / بعيدة ، وعلى الرغم من تباين الأرقام المحددة ، كانت الاتجاهات العامة في النتائج هي نفسها).

في الجدول ، "eq" - تحصل نقطتان بأقرب عمق على نفس القيمة في المخزن المؤقت للعمق ، و "مبادلة" - يتم تبديل نقطتين بأقرب عمق.

	مصفوفة عرض الإسقاط المركبة		عرض منفصل ومصفوفات الإسقاط
	float32	int24	float32	int24
قيم Z غير المتغيرة (اختبار التحكم)	0٪ مكافئ 0 ٪ مبادلة	0٪ مكافئ 0 ٪ مبادلة	0٪ مكافئ 0 ٪ مبادلة	0٪ مكافئ 0 ٪ مبادلة
الإسقاط القياسي	45 ٪ مكافئ 18 ٪ مبادلة	45 ٪ مكافئ 18 ٪ مبادلة	77 ٪ مكافئ 0 ٪ مبادلة	77 ٪ مكافئ 0 ٪ مبادلة
لانهائي بعيدا	45 ٪ مكافئ 18 ٪ مبادلة	45 ٪ مكافئ 18 ٪ مبادلة	76 ٪ مكافئ 0 ٪ مبادلة	76 ٪ مكافئ 0 ٪ مبادلة
عكس ض	0٪ مكافئ 0 ٪ مبادلة	76 ٪ مكافئ 0 ٪ مبادلة	0٪ مكافئ 0 ٪ مبادلة	76 ٪ مكافئ 0 ٪ مبادلة
لانهائي + عكس- Z	0٪ مكافئ 0 ٪ مبادلة	76 ٪ مكافئ 0 ٪ مبادلة	0٪ مكافئ 0 ٪ مبادلة	76 ٪ مكافئ 0 ٪ مبادلة
معيار + GL ستايل	56 ٪ مكافئ 12 ٪ مبادلة	56 ٪ مكافئ 12 ٪ مبادلة	77 ٪ مكافئ 0 ٪ مبادلة	77 ٪ مكافئ 0 ٪ مبادلة
لانهائي + GL النمط	59 ٪ مكافئ 10 ٪ مبادلة	59 ٪ مكافئ 10 ٪ مبادلة	77 ٪ مكافئ 0 ٪ مبادلة	77 ٪ مكافئ 0 ٪ مبادلة

أعتذر عن حقيقة أنه بدون رسم بياني ، يوجد بعد كبير جدًا هنا ولا يمكننا بناءه! على أي حال ، بالنظر إلى الأرقام ، فإن الاستنتاجات التالية واضحة:

• في معظم الحالات ، لا يوجد فرق بين كثافة عازلة int العائمة . الأخطاء الحسابية لحساب أخطاء تجاوز العمق في التحويل إلى int. جزئيًا لأن float32 و int24 متساويان تقريبًا ULP (الوحدة الأقل دقة هي المسافة إلى أقرب رقم مجاور) بمقدار [0.5.1] (نظرًا لأن float32 يحتوي على سرعته 23 بت) ، لذلك لا تتم إضافة خطأ في التحويل على نطاق العمق بأكمله تقريبًا في كثافة العمليات.
• في معظم الحالات ، يؤدي الفصل بين مصفوفات العرض والإسقاط (باتباع توصيات Upchurch و Desbrun) إلى تحسين النتيجة. على الرغم من أن معدل الخطأ الإجمالي لا ينخفض ​​، فإن "المقايضات" تصبح قيمًا متساوية ، وهذه خطوة في الاتجاه الصحيح.
• الطائرة البعيدة لانهائية يغير قليلا من وتيرة الأخطاء. تنبأ Upchurch و Desbrun بتخفيض بنسبة 25٪ في تكرار الأخطاء العددية (أخطاء الدقة) ، لكن هذا لا يبدو أنه يؤدي إلى انخفاض في تكرار أخطاء المقارنة.

ومع ذلك ، فإن النتائج المذكورة أعلاه ليست حقيقية بالمقارنة مع السحر عكس Z. تحقق:

• Reversed-Z مع المخزن المؤقت عمق تعويم يعطي معدل خطأ صفر في الاختبار. الآن ، بالطبع ، يمكنك الحصول على بعض الأخطاء إذا استمرت في زيادة الفاصل الزمني لقيم عمق الإدخال. ومع ذلك ، فإن عكس Z مع تعويم أكثر دقة يبعث على السخرية من أي خيار آخر.
• Reversed-Z مع مخزن مؤقت للعدد الصحيح يكون بنفس جودة خيارات الأعداد الصحيحة الأخرى.
• تقوم Reversed-Z بطمس التمييز بين مصفوفات العرض / الإسقاط المركبة والمنفصلة ، والطائرات البعيدة المحدودة وغير المحدودة. بمعنى آخر ، مع عكس Z ، يمكنك مضاعفة الإسقاط بمصفوفات أخرى ، واستخدام أي مستوى بعيد تريد ، دون المساس بالدقة.

الخاتمة

أعتقد أن الاستنتاج واضح. في أي موقف ، عند التعامل مع إسقاط المنظور ، ما عليك سوى استخدام المخزن المؤقت لعمق الطفو و Z العكسي ! وإذا كنت غير قادر على استخدام المخزن المؤقت لعمق الطفو ، فلا يزال عليك استخدام عكس Z. هذه ليست حلا سحريا لجميع العلل ، خاصة إذا كنت تخلق بيئة منفتحة على العالم بمدى عمق عميق. لكن هذه بداية رائعة.