مهلا ، مداخن كاملة ، دعونا تدريب المهارات. أقترح العجن التلفيف ، ويبدو لي ، من المثير للاهتمام القيام بذلك باستخدام نموذج مختلف ، غير عادي. يمتلك معظم المطورين مهارة متطورة من الخوارزمية - تتحول المهمة إلى طوب تحتاج إلى الاتصال ، للتفكير في تسلسل الحركات التي تؤدي إلى الاستنتاج المرغوب.
هنا ، قبل أسبوع ، تم ذكر المقدمة ، أود أن أجيب أن لغة Prolog مناسبة لحل المشكلات. لقد سبق أن تطرقت إلى هذا الموضوع ، واستشهدت بالعديد من حلول المهام العشوائية المتاحة لي من أحد المواقع التي تتضمن مهام للخوارزميات ، وأود أن أوضح أن أي حل معقد متوفر بلغة تعريفية ، وأنه لا يمكن أن يكون أبطأ (جيدًا ، وربما بشكل ملحوظ ليس بطيئا جدا).
استغرق الأمر وقتًا طويلاً للوصول إلى المشكلة التالية ، وقد تم بالفعل تلقي الحل الأول ، وأثبت المشكلة وأكتشف بطئها.
مقدمة مقدمة مثيرة للاهتمام حيث يمكنك إنشاء برنامج استنتاجي يعرض الكثير من الحلول ويمكن حتى الحد منه ، لكنه لا يوفر وسيلة للتكرار ،
سيتم تطوير الخوارزمية حلالا مترجم فوري.
لذلك ، المهمة هي :
- محاصرة مياه الأمطار ii
بالنظر إلى مصفوفة mxn من الأعداد الصحيحة الموجبة التي تمثل ارتفاع كل خلية وحدة في خريطة الارتفاع ثنائي الأبعاد ، قم بحساب حجم الماء الذي يمكن فخه بعد المطر.
ملاحظة:
كلا m و n أقل من 110. ارتفاع كل خلية وحدة أكبر من 0 وأقل من 20،000.
مثال:
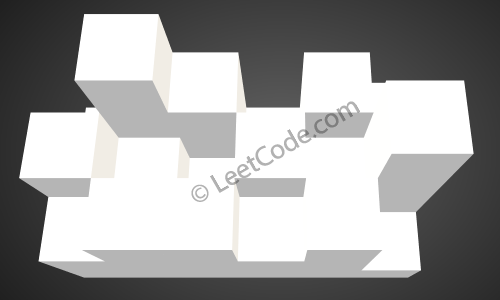
بالنظر إلى خريطة ارتفاع 3x6 التالية:
[
[1،4،3،1،3،2] ،
[3،2،1،3،2،4] ،
[2،3،3،2،3،1]
]
عودة 4.
بعد محاولات طويلة لصياغة حل ، جئت إلى هذه الصيغة:
من الضروري سكب الماء كحد أقصى في كل خلية ، والتي لن تتسرب منه . أقترح صب كمية معينة من الماء في كل خلية ، ولكن ذلك أقل من الحد الأقصى لقيمة كل ما هو ممكن.
اتضح مثل هذا:
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.
يأخذ هذا المسند قائمة المدخلات (المصفوفة) ، ويحولها إلى حل ، إلى مصفوفة توجد فيها قيم أخرى ستكون إجابة صحيحة. ثم يأخذ تقييم آخر هاتين القائمتين عنصرًا بالعنصر ويجد المبلغ الإجمالي.
repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).
سيأخذ هذا المسند أحد الحلول ، ويتحقق مما إذا كان يتم ملؤه "بشكل طبيعي" ، إذا كان يرضي حالة المشكلة ، فهذا هو الحل.
هذه هي طريقة "إنشاء والتحقق" ، نقول أن القيمة في مثل هذه المجموعة ونقوم بمراجعة جميع عناصر هذه المجموعة ، والتحقق من نوع من شروط الخروج.
لذا ، سوف أحصل على حل جديد مع المسندات (Vals ، X0 ، X1) ، وهنا في المقام الأول قائمة بجميع الارتفاعات المحتملة الموجودة في هذه المصفوفة ، والتي سنختار منها الارتفاعات المحتملة لكل خلية. وفقًا لتحليل اختبارات الإدخال ، تبين أنه من الممكن في هذه المشكلة ملء الخلية بأكملها ، إذا أمكن إدخال الكثير من الماء حولها بحيث يتم سكبها "فوق الرأس".
بشكل إجمالي ، يبدو هذا المسند أكثر تعقيدًا ، فمن الضروري معالجة ثلاثة أسطر من الخطوط التي تشكل مربعًا واحدًا 3 × 3 (نعم ، لا يوجد صفيف في Prolog ، ولكنه يشبه وصف بيانات الإدخال ، ونحن نستخدمه في البرمجة التصريحية ، قد لا تعرف مؤشرات العناصر في الصفيف ، لا يوجد سوى قائمة برأسها وذيلها ، لذلك ما عليك سوى وصف قالب يطابق مواصفات الإدخال).
puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).
هذه هي الطريقة التي يتم بها التعبير عن تجاوز للمصفوفة ، والتي يمكنك منها أن تأخذ الصفوف الثلاثة الأولى (وأكثر) ، والتي يمكنك من خلالها ، من اليسار إلى اليمين ، ثلاثة عناصر من العناصر ، وبين الجيران الثمانية ستكون هناك خلية واحدة [Itaya] [Utaya] للمناظر الطبيعية. بمساعدة sel_biger (R2 ، V ، R21) تم إنشاء معنى جديد لهذه الخلية.
يمكن ضبط هذه القيمة على الخلية الحالية ، ويمكن أن تكون واحدة من الارتفاعات المحتملة ، وحتى يتم فرز القائمة بترتيب تنازلي ، بحيث تكون الأولى هي أعلى ارتفاع متاح على الإطلاق ، ثم بعد ذلك:
sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).
لقد كان وصفًا لـ "منشئ القرار" ، ومن ثم تحتاج إلى التأكد من أن المصفوفة التي تم الحصول عليها ، من المرتفعات المعبأة بشكل تعسفي في كل نقطة ، تشبه الإجابة التي نطلبها.
وكان لا بد من إيجاد مثل هذه الحالة التي يستقر فيها الماء في الثقوب ، سأحاول وضعه على هذا النحو:
من تسع قيم للمربع هي ثلاثة في ثلاثة ، في الوسط يجب أن يكون هناك دائمًا هذا الارتفاع بحيث لا يتعارض مع خريطة المدخلات ، بحيث لم يتم الحصول على تغيير التوازن الذي كان موجودًا في الأصل في هذه الخلايا ، إذا كان هناك ارتفاع ، فلا ينبغي أن يكون هناك خلايا فوقه ، حتى لو كل شيء سوف يغمر بالماء ، ثم هنا يمكننا القول أن الخلية العالية يجب أن تبقى من تلقاء نفسها أو أن يتم استبدالها بقيمة أعلى ، لكنها تساوي جميع الجيران ، أي يجب أن تتجاوز الخلايا الموجودة على اليسار ، إلى اليمين ومن الأعلى إلى الأسفل من التيار أو تكون متساوية ، إذا كان هناك المزيد من الماء في الخلية ، ثم فقط إذا ارتفعت حول ...
ويبدأ المسندان الأخيران ، اللذان يأخذان مصفوفة الإدخال ، البحث عن نتيجة مناسبة ، وطرح مجموع العناصر فيما بينها ، والعثور على المبلغ النهائي المطلوب في المشكلة:
diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %% , sums(X,S):-reptest(X,X1),diffall(X,X1,S).
سأبين الاختبارات التي قدمها الموقع .
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). % balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). % , 33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). % , % equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).
كان علي أن أعلق على الاختبارات. لم يذهب كل من خلال.
المهمة هي كيفية تسريعها؟
لا يمكن العثور على بعض الحلول ، بسبب البحث الطويل عن الحلول ، يتم إنشاؤها ببطء شديد في هذا الترتيب ، وهنا قد يكون التعقيد n! ، يتم فرز جميع القيم الممكنة لكل خلية في المصفوفة.
من المريح التعبير عن هذه المهمة في نظام برمجة في قيود ، فقط في Prolog يطلق عليه مثل هذا: CLP (FD): قيود البرمجة المنطقية على المجالات المحددة.
clp (fd) هي مكتبة مضمنة في توزيع SWI-Prolog القياسي. إنه يحل المشكلات التي تنطوي على مجموعات من المتغيرات ، حيث تحتاج العلاقات بين المتغيرات إلى الرضا.
>>
أقوم بصياغة المشكلة مثل هذا:
نحتاج إلى مثل هذه القائمة ، حيث يكون كل عنصر من عناصر مجموعة القيم أكبر من أو يساوي قيمته القصوى في جميع أنحاء الخريطة ، مع الأخذ في الاعتبار القيد بأن العناصر يجب أن تكون موجودة بوضوح بترتيب السائل المنسكب المقابل.
هذه هي الطريقة التي أقوم بها من قائمة المدخلات ، وهي قائمة جديدة أصبحت عناصرها غير معروفة في نطاق معين (من قيمة R2 للعنصر الحالي إلى الحد الأقصى لقيمة V)
عند الإدخال ، قائمة بالقوائم ؛ عند الإخراج ، قائمة جديدة بأقصى ترتيب للقيم ،
التي تلبي الحد من balns توازن السوائل:
checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
هذا هو كل من مولد وفحص في نفس الوقت ، ويشار إلى أن العناصر في مثل هذه المجموعة ، ثم فرض الاختيار تدريجيا ، يتم تضييق هذه المجموعة. علاوة على ذلك ، لا يزال هناك شيء ، ويمكن أن يكون "ملحوظ" ، أي تعيين القيم الصحيحة التي ترضي مجموع جميع القيود. استدعاء وضع العلامات ([لأسفل] ، FX2) يفرض ملء (الاتصال) المتغيرات غير معروف بقيم محددة ، وقد يكون هناك العديد من هذه الخيارات ، لكننا سنأخذ دائمًا الخيار الأول ، حيث قيل إن جميع المتغيرات تتحرك لأسفل في البحث ، من الحدود العليا ، هذه هي خيارات البحث [أسفل].
وهناك يمكنك رؤية الإعدادات المعقدة مثل:16.2.1. استراتيجية اختيار متغير
تتيح لك استراتيجية التحديد المتغير تحديد أي متغير من Vars يتم تمييزه بعد ذلك وهو واحد من:
أقصى اليسار - تسمية المتغيرات بالترتيب الذي تحدث به في Vars. هذا هو الافتراضي.
وما يليها فشل أولا. قم بتسمية المتغير الموجود في أقصى اليسار بأصغر مجال تالي ، من أجل اكتشاف عدم إمكانية الوصول مبكرًا. غالبًا ما تكون هذه إستراتيجية جيدة عندما تكون هناك مجالات صغيرة للمتغيرات اللاحقة عند اختيار المتغير الأول.
ffc من بين المتغيرات ذات النطاقات الأصغر ، يُسمى التالي في أقصى اليسار المشارك في معظم القيود. يجب أن يؤدي تطبيق قيد إلى إزالة الشجرة الفرعية ، لذلك يمكن أن تكون هذه استراتيجية جيدة.
قم بتسمية المتغير الموجود في أقصى اليسار والذي يكون الحد الأدنى هو الأدنى التالي. لاحظ أن هذا هو min / 0 ، يختلف عن min / 1 ، والذي يحدد حل الحل ويتم مناقشته في القسم السابق أعلاه. هذا تكتيك جيد إذا كنت تحاول تقليل بعض القيمة العالمية التي من المحتمل أن تكون أقل إذا كانت المتغيرات المختلفة (على سبيل المثال ، حل التكلفة الأدنى).
قم بتسمية المتغير الموجود في أقصى اليسار والذي يكون الحد الأعلى هو الأعلى التالي. هذا أيضًا يختلف عن الحد الأقصى / 1. وتنطبق نصيحة min على max عند محاولة تعظيم القيمة العالمية.
16.2.2. ترتيب القيمة
ترتيب القيمة هو واحد من:
up جرب عناصر مجال المتغير المختار بترتيب تصاعدي. هذا هو الافتراضي.
أسفل حاول عناصر المجال بالترتيب التنازلي.
من الواضح ، إذا كان لديك توزيع غير متماثل ، مثلما أوضحنا في كيفية وضع العلامات المذكورة أعلاه بكفاءة ، فجرّب العناصر الأكثر شيوعًا من الدرجة الأولى.
16.2.3. استراتيجية المتفرعة
استراتيجية المتفرعة هي واحدة من:
الخطوة لكل متغير X ، يتم الاختيار بين X = V و X # \ = V ، حيث يتم تحديد V بواسطة خيارات ترتيب القيمة. هذا هو الافتراضي.
التعداد لكل متغير X ، يتم الاختيار بين X = V_1 ، X = V_2 وما إلى ذلك ، لجميع القيم V_i لمجال X. يتم تحديد الترتيب بواسطة خيارات ترتيب القيمة.
bisect لكل متغير X ، يتم الاختيار بين X # = <M و X #> M ، حيث M هي نقطة الوسط للمجال X. حدد هذا الخيار إذا كانت العديد من المتغيرات هي التحديدات بين مجموعة من الأعداد الصحيحة ، قيمة ، بدلاً من واحدة من بين مجموعة من القيم المذكورة (مثل النسب المئوية ، مقابل a = 0 ، b = 1 ، c = 2)
الآن في الواقع ، ما "متوازن" هو عندما لا يتدفق الماء المصب من خلية إلى أخرى. هذه هي مراسلة الترتيب الأصلي للعناصر. قد تعتقد أن ملء الخلايا سيحافظ على شكل المنظر الطبيعي الأصلي ، مما يعني أنه إذا كان هناك جدار ، فإنه يمكن تغطيته بالماء في الأعلى ، بحيث يصبح بالضرورة مساويا لجميع جيرانه ، أو إذا لم يكن جدارًا مغطى بالماء ...
النظر في المواقف المتوازنة:
، إذا غمرت الخلية ، ثم بجانب نفسه أو أعلى (فجأة هو الجدار).
- إذا كانت الخلية مساوية للخلية المجاورة ، فينبغي أن تكون مساوية للخلية المجاورة.
- وفي الحالة القصوى ، لم تغير الخلية معناها ، ولا يزال أي نوع من الجيران لديها:
هذه هي الطريقة التي يمكنك بها نقل موقفك إلى المهمة في البرنامج. ليس من الضروري بالنسبة لي أن أفكر في خوارزمية قرار ، من المهم تقديم وصف صحيح للنتيجة ، لضبط جميع القيود الأولية (مجموعات القيم) بشكل صحيح. يمكن ببساطة خلط هذا النهج مع البحث المعتاد مع الإرجاع والتكرار المتأصلين في Prolog. هذه طريقة لصياغة برامج تعريفية أكثر من استخدام أساليب Prolog الكلاسيكية .
سأقدم الحل الذي تم الحصول عليه ، مع مجموعة من الاختبارات:
:- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
والمزيد من الاختبارات :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).
كانت هذه اختبارات من الموقع ، فقط أول 30 قطعة. والنتيجة ممتازة ، ويتم حل المشكلة ، وحتى بسرعة ، كل الأوقات تصل إلى ثانية واحدة.
يمكنك التحقق ...
كخلاصة
تتضمن البرمجة التصميمية إضفاء الطابع الرسمي التفصيلي على المهمة ، وسيبحث المحلل عن الحل الأكثر فاعلية الذي يفي بالشروط.
أعمق قليلاً في الموضوع ، يمكنك فتح minizinc ، وهي لغة برمجة مضمنة في هذا النموذج. لقد صاغوا العديد من المعاني ، والقيود المشار إليها ، وفويلا ، الجواب. أنها تحل سودوكو ، مهام تلوين الخريطة ، عمل الجدولة ، مشاكل الموارد ، الجدولة. أقترح تدريب ...