الرياضيات في Gamedev بسيطة. التثليث والمثلث. الصافي في الوحدة

مرحبا بالجميع! اسمي Grisha وأنا مؤسس CGDevs. Math هي أداة رائعة جدًا عند تطوير الألعاب. ولكن إذا قلنا أنه من الصعب إدارتها دون فهم المتجهات والمصفوفات ، فإن خوارزميات التثليث ليست بالأمر الضروري ، ولكن يتم حلها مع عدد كبير من المشكلات المثيرة للاهتمام. أود اليوم أن أتحدث عن أداة مهمة إلى حد ما في الهندسة الحاسوبية ، مثل التثليث وتطبيقاتها في صناعة الألعاب. بالإضافة إلى ذلك ، كتبت منفذًا وبعض الأغلفة لمكتبة Triangle.Net الممتازة من أجل Unity. إذا كانت مهتمة - مرحبا بكم في القط. رابط لجيثب المرفقة.

ما هو التثليث؟

في الحالة العامة ، التثليث هو قسم من كائن هندسي إلى مثلثات. هذا المفهوم في حد ذاته بسيط جدا. مثال أساسي على التثليث في حالة محركات اللعبة هو شبكة. بالمعنى الدقيق للكلمة ، يمكن أن تتكون الشبكة ليس فقط من المثلثات ، ولكن في محركات اللعبة لعدة أسباب ، فهي عبارة عن شبكات تتألف من مثلثات يتم أخذها.



التثليثات مختلفة ، ولكن أحد أنواع التثليث الأكثر شعبية هو تثليث Delaunay. يتميز هذا النوع من التثليث بخاصية أنه في الدائرة المحاطة حول كل مثلث ، تقع رؤوس هذا المثلث فقط.

لماذا هم بحاجة؟

بشكل عام ، خارج صناعة الألعاب ، باستخدام التثليث ، يتم حل عدد كبير من المشاكل. في تطوير اللعبة ، تتمثل المهمة الأولى التي تتبادر إلى الذهن في شبكة التنقل. Navmesh هي بنية بيانات تحدد مقدار المساحة التي يمكن للاعب السير فيها. إنه يتجنب المهام الحسابية المعقدة مثل تحديد الاصطدامات مع جزء من البيئة.

المشكلة الثانية المثيرة للاهتمام التي يمكن حلها باستخدام تثليث Delaunay في تطوير اللعبة هي توليد التضاريس والكائنات الممثلة كمجموعة من النقاط. تتمثل الميزة الرئيسية لتثليث Delaunay في هذه الحالة ، استنادًا إلى خصائصه ، في أنه يسمح لك بتجنب مثلثات حادة جدًا من شأنها أن تتداخل وتنتج مصنوعات على الترين.



بالإضافة إلى ذلك ، باستخدام تثليث Delaunay المقيد والخوارزميات مثل الخوارزمية الثانية لـ Chew وخوارزمية Ruppert ، يمكنك إنشاء شبكات أفضل للتراين وإنشاء شبكات جيدة لتطبيق آخر - طريقة العناصر المحددة.

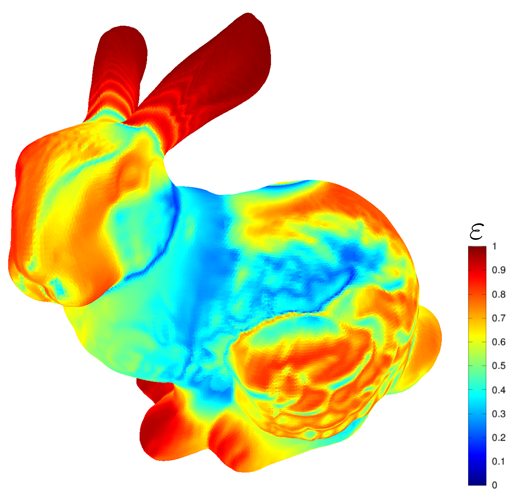
طريقة العناصر المحددة بحد ذاتها هي إحدى الطرق التي يتم بها حل مشاكل الفيزياء التطبيقية. في gamedev ، يسمح لك بحل العديد من المشاكل المرتبطة بمحاكاة التشوهات ، ومحاكاة السوائل وغيرها من الأشياء التي تستخدم للخاصة. الآثار. عادةً لتسجيل التأثيرات في الرسوم المتحركة ، لأنه في الوقت الفعلي تتميز الطريقة بتعقيد حسابي كبير للغاية. من التفاصيل المهمة عند استخدام الطريقة أن خطأ الطريقة يعتمد على زوايا المثلثات في الشبكة. إذا كانت هناك زوايا حادة جدًا في الشبكة ، فإن الطريقة تعطي خطأً كبيراً ، ولهذا السبب فإن الخوارزميات المذكورة أعلاه مطلوبة.



وبطبيعة الحال ، بشكل عام ، جيل شبكة الإجرائية. على سبيل المثال ، يعرض مشروع github مشهدًا له القدرة على رسم الشبكات. بعض الألغاز المادية تستخدم هذا التطبيق كما الميكانيكا الأساسية. لكن بالإضافة إلى ذلك ، تسمح خوارزميات التثليث باستخدام التوليد الإجرائي لحل مشكلات مثل التدمير الإجرائي وما إلى ذلك.

بالإضافة إلى التثليث gamedev تستخدم في الشبكات ، رؤية الكمبيوتر ، العديد من الخوارزميات التحليلية ، وكذلك في مشاكل الهندسة الحاسوبية ، مثل الجمع بين المضلعات وإزالتها من بعضها البعض (وهو أمر مفيد في كثير من الأحيان في المشاكل الناشئة في تطوير الألعاب)

لقطة الأذن مع الثقوب

ربما واحدة من أبسط خوارزميات التثليث. لا يعطي أفضل شبكة ولديه أكبر تعقيد حسابي O (n ^ 2) في أسوأ الحالات.

يمكنك قراءة المزيد عنها في هذا المقال.

بوير - واتسون الخوارزمية

خوارزمية تولد تثليث Delaunay على مجموعة من النقاط. بشكل عام ، كما هو الحال مع معظم خوارزميات Delaunay ، إذا تم تطبيقه بشكل صحيح ، فإن التعقيد الحسابي هو O (n log n) ، حيث n هو عدد الرؤوس. لكن في بعض الحالات قد يستغرق الأمر O (n ^ 2).

العيوب المتعلقة بقطع الأذن هي أن هذه الخوارزمية تبني التثليث المحدب وفي التنفيذ الأساسي لا ينطوي على ثقوب في الشبكة الناتجة.

Delaunay معالجة الصقل

الخوارزمية الثانية لـ Chew وخوارزمية Ruppert عبارة عن خوارزميات تسمح لك بإدخال قيود في تثليث Delaunay وتعيين الحد الأدنى لزاوية المثلث في الشبكة. من التفاصيل المهمة للخوارزميات أنها يمكن أن تدخل حلقة لا نهائية ومضمونة لإعطاء نتائج في زوايا تتراوح بين 20.7 درجة و 29 درجة تقريبًا. تعد القدرة على تحديد زاوية دنيا مهمة في حل المشكلات الموضحة أعلاه.

يتم تطبيق الخوارزمية الثانية لـ Chew في الحزمة المجانية www.cs.cmu.edu/~quake/triangle.html ومنفذها على .Net archive.codeplex.com/؟p=triangle

مثلث. صافي من أجل الوحدة

حسنًا ، لأنه بمساعدة التثليثات ، يمكنك حل الكثير من المهام الرائعة ، في أيام العطلات ، أردت أن أستخدم برنامج التغليف الخاص بي من أجل الوحدة ، حتى يكون لدي دائمًا أداة مفيدة في متناول اليد. في هذا التطبيق ، تعمل خوارزمية التثليث في المتوسط ​​لـ O (n) ، وفي أسوأ الحالات بالنسبة إلى O (n * log n) ، حيث n هو عدد الرؤوس. على سبيل المثال ، عند اختبار رؤوس 1kk المنتشرة عشوائيًا عبر مربع ، قامت الوحدات الموجودة في المحرر على Intel Core i7-8700 ببناء شبكة بمعدل 7.56 ثانية في المتوسط.

الاختلافات الرئيسية عن المكتبة الأصلية في وجود طرق التمديد المصممة خصيصًا للوحدة ، بالإضافة إلى الاستعاضة عن مزدوجة مع تعويم في المكتبة بأكملها (+ زوجين من المشغلين المحددين للصب). مزدوج في الوحدة ، ليس له معنى كبير. إذا أخذنا في الاعتبار عمليات المحاكاة البدنية ، فسأستخدم تطبيقًا منفصلاً على مكتبة plus ، وكنتيجة للحسابات التي قدمت Unity بالفعل لمجرد التصور. وأعدت أيضًا تسمية نوع الشبكة إلى TriangleNetMesh حتى لا تتعرض للضرب بالنسبة إلى Mesh من Unity. نعم ، هم بالفعل في مساحة اسم مختلفة ، لكن مع ذلك ، أعتقد أن القادمين الجدد سوف يتأثرون قليلاً بحقيقة أننا بمساعدة شبكة واحدة نحصل على أخرى.

جوهر المكتبة هو أنه يجب عليك أولاً تحديد ما يسمى المضلع. ثم ، بناءً عليه ، قم بإنشاء الشبكة بالفعل. من أجل أن يعمل هذا مع هياكل بيانات الوحدة ، تم تقديم العديد من طرق التمديد.



على سبيل المثال التوضيحي والاستخدام ، تم إنشاء مشهد تجريبي خاص مع إمكانية رسم الشبكات. يمكنك التعرف عليه ومنفذ المكتبة في مشروع جيثب.

شكرا لاهتمامكم! آمل أن يكون المنفذ والمقال مفيدًا لشخص ما وسيصبح من الواضح قليلاً سبب الحاجة إلى التثليث ومعرفة الرياضيات ككل. سأحاول الاستمرار في الكشف عن التطبيقات والأساليب لحل المشكلات الرياضية المختلفة في تطوير اللعبة. في الهندسة الحاسوبية نفسها لا يزال هناك الكثير من الأشياء المثيرة للاهتمام ، ولكن إلى جانب ما زال هناك العديد من الأقسام الأخرى المثيرة للاهتمام في الرياضيات العليا.