نظرية السعادة. الإحصاء كطريقة علمية لعدم معرفة أي شيء

ما زلت أطلع قرّاء هبر على فصول كتابه "نظرية السعادة" بعنوان "الأسس الرياضية لقوانين المعنى". هذا لم ينشر بعد كتابًا علميًا شهيرًا ، يوضح بشكل غير رسمي كيف تسمح لك الرياضيات بالنظر إلى العالم وحياة الناس بدرجة جديدة من الوعي. إنه لمن يهتم بالعلم ولمن يهتم بالحياة. وبما أن حياتنا معقدة ولا يمكن التنبؤ بها إلى حد كبير ، فإن التركيز في هذا الكتاب ينصب أساسًا على نظرية الاحتمالات والإحصاءات الرياضية. هنا لم يتم إثبات النظريات ولم يتم تقديم أساسيات العلوم ، وهذا ليس كتابًا مدرسيًا على الإطلاق ، ولكن ما يسمى بالعلم الترويحي. لكن هذه المقاربة شبه المرحة على وجه التحديد هي التي تسمح لنا بتطوير الحدس وإلقاء المحاضرات على الطلاب بأمثلة حية ، وأخيرا ، شرح لغير المتخصصين في الرياضيات وأطفالنا ما وجدناه مثيرا للاهتمام في علومنا الجافة.


هذا الفصل يدور حول الإحصاءات والطقس وحتى الفلسفة. لا تقلق ، فقط قليلا. لا مزيد من التي يمكن استخدامها ل tabletalk في مجتمع لائق.

الأرقام مخادعة ، خاصة عندما أفعلها بنفسي ؛ في هذه المناسبة ، فإن البيان المنسوب إلى دزرائيلي صحيح: "هناك ثلاثة أنواع من الأكاذيب: الأكاذيب والأكاذيب الفاضحة والإحصاءات".
مارك توين

كم مرة في الصيف نخطط للذهاب في الهواء الطلق ، أو المشي في الحديقة أو الحصول على نزهة ، وبعد ذلك يكسر المطر خططنا ، ويسجننا في المنزل! وكذلك ، إذا حدث هذا مرة أو مرتين في الموسم ، في بعض الأحيان يبدو أن الطقس يتابع عطلة نهاية الأسبوع ، حيث يصل إلى السبت أو الأحد مرارًا وتكرارًا!

نشر باحثون أستراليون مقالًا حديثًا نسبيًا: "دورات أسبوعية لذروة درجة الحرارة وكثافة الجزر الحرارية الحضرية". تم التقاطها من قبل وسائل الإعلام وأعادت طباعة النتائج مع العنوان التالي: "ألا تظن! لقد وجد العلماء أن الطقس في عطلات نهاية الأسبوع أسوأ حقًا من أيام الأسبوع ". توفر الورقة المذكورة إحصائيات عن درجة الحرارة وهطول الأمطار على مدار سنوات عديدة في عدة مدن في أستراليا ، وتكشف بالفعل عن انخفاض في درجة الحرارة خلال ساعات معينة يومي السبت والأحد. بعد ذلك ، يتم تقديم تفسير يربط بين الطقس المحلي ومستوى تلوث الهواء بسبب زيادة حركة المرور. قبل ذلك بفترة قصيرة ، أجريت دراسة مماثلة في ألمانيا وأدت إلى نفس الاستنتاجات تقريبًا.

توافق ، الكسور درجة هو تأثير خفية جدا. نحن نشتكي من سوء الأحوال الجوية يوم السبت الذي طال انتظاره ، ونحن نناقش ما إذا كان اليوم مشمسًا أو ممطرًا ، وهذه الحقيقة أسهل في التسجيل ، ولاحقًا تذكرها ، حتى دون وجود أدوات دقيقة. سنجري دراستنا الصغيرة حول هذا الموضوع ونحصل على نتيجة رائعة: يمكننا أن نقول بثقة أننا لا نعرف ما إذا كان يوم الأسبوع والطقس مرتبطان في كامتشاتكا. عادةً ما لا تندرج الدراسات ذات النتائج السلبية على صفحات المجلات وفي موجز الأخبار ، ولكن من المهم أن تفهم أنت وأنا ، على أي أساس ، بشكل عام ، يمكنني أن أقول بثقة شيئًا عن العمليات العشوائية. وفي هذا الصدد ، النتيجة السلبية ليست أسوأ من النتيجة الإيجابية.

كلمة في الدفاع عن الإحصاءات

يتم إلقاء اللوم على الإحصائيات عن كتلة الذنوب: في الأكاذيب وفي إمكانيات التلاعب ، وأخيرا في عدم الفهم. لكنني أريد حقًا إعادة تأهيل هذا المجال من المعرفة ، لإظهار مدى صعوبة المهمة التي من أجلها ، ومدى صعوبة فهم الإجابة التي تقدمها الإحصاءات.

تستخدم نظرية الاحتمالات معرفة دقيقة للمتغيرات العشوائية في شكل توزيعات أو حسابات توافقية شاملة. أؤكد مرة أخرى أنه من الممكن أن يكون لديك معرفة دقيقة بمتغير عشوائي. ولكن ماذا لو كانت هذه المعرفة الدقيقة غير ممكنة بالنسبة لنا ، والشيء الوحيد الذي لدينا تحت تصرفنا هو الملاحظة؟ يمتلك مطور الدواء الجديد عددًا محدودًا من الفحوصات ، ولم يكن لدى مُنشئ نظام التحكم في تدفق حركة المرور سوى سلسلة من القياسات على الطريق الحقيقي ، وعالم الاجتماع لديه نتائج الاستطلاعات ، علاوة على ذلك ، يمكنه التأكد من أنه عند الإجابة على بعض الأسئلة ، فإن المشاركين كذب فقط.

من الواضح أن ملاحظة واحدة لا تعطي أي شيء على الإطلاق. اثنان - أكثر بقليل من لا شيء ، ثلاثة أو أربعة ... مائة ... كم عدد الملاحظات التي تحتاجها للحصول على أي معلومات عن متغير عشوائي يمكنك التأكد من دقة الرياضيات؟ وأي نوع من المعرفة سيكون؟ على الأرجح ، سيتم تقديمه في شكل جدول أو رسم بياني يتيح تقييم بعض معلمات المتغير العشوائي ؛ وتسمى هذه الإحصاءات إحصائيات (على سبيل المثال ، مجال التعريف أو الوسط أو التباين أو عدم التماثل وما إلى ذلك). ربما يكون النظر إلى الرسم البياني قادرًا على تخمين الشكل الدقيق للتوزيع. لكن الاهتمام! - جميع نتائج الملاحظة نفسها ستكون متغيرات عشوائية! طالما أننا لا نملك معرفة دقيقة بالتوزيع ، فإن كل نتائج الملاحظة لا تقدم لنا سوى وصف احتمالي للعملية العشوائية! الوصف العشوائي لعملية عشوائية لا يزال غير مرتبك هنا ، أو حتى يريد الخلط بينه وبين قصد!

ما الذي يجعل الإحصاءات الرياضية علمًا دقيقًا؟ تسمح لنا أساليبها بإنهاء جهلنا في إطار محدود بشكل واضح وإعطاء قدر من الثقة يحسب أنه ، في هذا الإطار ، تتوافق معرفتنا مع الحقائق. هذه هي اللغة التي يمكن للمرء أن سبب حول المتغيرات العشوائية غير معروفة بحيث منطق المنطقي. يعد هذا النهج مفيدًا جدًا في الفلسفة أو علم النفس أو علم الاجتماع ، حيث يكون من السهل جدًا الانخراط في التفكير والمناقشة المطوّلين دون أي أمل في اكتساب المعرفة الإيجابية ، ولا سيما البرهان. يتم تخصيص الكثير من الأدب لمعالجة البيانات الإحصائية المختصة ، لأنها أداة ضرورية للغاية للأطباء وعلماء الاجتماع والاقتصاديين والفيزيائيين وعلماء النفس ... باختصار ، لجميع العلماء الذين يبحثون في "العالم الحقيقي" ، والذي يختلف عن الرياضيات المثالية فقط في درجة جهلنا بها.

ألقِ نظرة أخرى على النص المكتوب على هذا الفصل وأدرك أن الإحصائيات ، التي يطلق عليها بشكل مخزي الدرجة الثالثة من الأكاذيب ، هي الأشياء الوحيدة التي تمتلكها العلوم الطبيعية. أليست هذه هي الشريعة الرئيسية لكون الكون! تستند جميع قوانين الطبيعة المعروفة لنا ، من المادية إلى الاقتصادية ، إلى النماذج الرياضية وخصائصها ، ولكن يتم التحقق منها بالطرق الإحصائية أثناء القياسات والملاحظات. في الحياة اليومية ، يقوم أذهاننا بعمل التعميمات ويلاحظ الأنماط ويعزل ويعترف بالصور المتكررة ، وربما يكون هذا هو أفضل ما يمكن لعقل الإنسان القيام به. هذا هو بالضبط ما يدرسه الذكاء الاصطناعي في هذه الأيام. لكن العقل يحفظ قوته ويميل إلى استخلاص استنتاجات من الملاحظات الفردية ، دون القلق بشأن دقة أو صحة هذه الاستنتاجات. في هذه المناسبة ، هناك بيان رائع متسق ذاتيا من كتاب ستيفن براست Isola: "الجميع يستخلص استنتاجات عامة من مثال واحد. على الأقل أفعل ذلك " . وبينما نتحدث عن الفن أو طبيعة الحيوانات الأليفة أو مناقشة السياسة ، لا يمكنك القلق بشأن هذا الأمر. ومع ذلك ، عند بناء طائرة أو تنظيم خدمة إرسال مطار أو اختبار دواء جديد ، لم يعد بإمكانك الرجوع إلى حقيقة "يبدو لي" و "يخبرني الحدس" و "كل شيء يحدث في الحياة". هنا عليك أن تقصر عقلك على إطار الأساليب الرياضية الصارمة.

كتابنا ليس كتابًا مدرسيًا ، ولن ندرس الأساليب الإحصائية بالتفصيل وسنقتصر على شيء واحد فقط - تقنية اختبار الفرضيات. ولكني أود أن أوضح مسار التفكير وشكل النتائج المميزة لهذا المجال من المعرفة. وربما لن يفهم بعض القراء ، الطالب المستقبلي ، سبب تعذّبه بالإحصاءات فحسب ، بل كل هذه الرسوم البيانية QQ وتوزيعات t و F ، ولكن هناك سؤالًا مهمًا آخر سيطرح: كيف يمكن معرفة ما - بالتأكيد عن حادث؟ وما الذي نتعلمه بالضبط باستخدام الإحصاءات؟

ثلاث حيتان من الإحصاءات

الركائز الرئيسية للإحصاءات الرياضية هي نظرية الاحتمالات ، وقانون الأعداد الكبيرة ، ونظرية الحد المركزي .

يشير قانون الأعداد الكبيرة ، في تفسير حر ، إلى أن عددًا كبيرًا من ملاحظات المتغير العشوائي يعكس توزيعه بشكل شبه مؤكد ، بحيث تميل الإحصاءات المرصودة: المتوسط ​​والتباين وغيرها من الخصائص إلى القيم الدقيقة المقابلة للمتغير العشوائي. بمعنى آخر ، فإن الرسم البياني للقيم المرصودة مع عدد لا حصر له من البيانات يميل بشكل شبه مؤكد إلى التوزيع الذي يمكننا اعتباره صحيحًا. هذا القانون هو الذي يربط التفسير "اليومي" لتردد الاحتمالات والنظرية ، كتدابير في فضاء الاحتمال.

تقول نظرية الحد المركزي ، مرة أخرى ، في تفسير حر ، أن أحد أكثر أشكال توزيع المتغير العشوائي هو التوزيع العادي (الجاوسي). تبدو الصياغة الدقيقة مختلفة: يتم وصف متوسط ​​القيمة لعدد كبير من المتغيرات العشوائية الحقيقية الموزعة بشكل متطابق ، بغض النظر عن توزيعها ، بالتوزيع العادي. عادةً ما يتم إثبات هذه النظرية باستخدام طرق التحليل الوظيفي ، لكننا سنرى لاحقًا أنه يمكن فهمها وتوسيعها من خلال تقديم مفهوم الإنتروبيا كمقياس لاحتمال حالة النظام: التوزيع الطبيعي لديه أكبر إنتروبيا مع أقل عدد من القيود. بهذا المعنى ، يكون الأمر مثاليًا عند وصف متغير عشوائي غير معروف ، أو متغير عشوائي ، وهو مزيج من العديد من المتغيرات الأخرى ، وتوزيعها غير معروف أيضًا.

يرتكز هذان القانونان على التقديرات الكمية لموثوقية معرفتنا استنادًا إلى الملاحظات. نحن هنا نتحدث عن تأكيد إحصائي أو دحض للافتراض ، والذي يمكن أن يتم من بعض الأسس الشائعة والنموذج الرياضي. قد يبدو هذا غريباً ، لكن في حد ذاته ، لا تنتج الإحصاءات معرفة جديدة. تتحول مجموعة من الحقائق إلى المعرفة فقط بعد بناء الروابط بين الحقائق التي تشكل بنية معينة. هذه الهياكل والعلاقات هي التي تسمح لنا بعمل تنبؤات وافتراضات عامة تستند إلى شيء يتجاوز الإحصاءات. وتسمى هذه الافتراضات الفرضيات . حان الوقت لتذكر واحد من قوانين المورفولوجيا ، افتراض البرسيج :

عدد الفرضيات المعقولة التي تشرح أي ظاهرة معينة لا حصر له.

تتمثل مهمة الإحصاء الرياضي في الحد من هذا العدد غير المحدود ، أو بالأحرى اختصارها إلى رقم واحد ، وليس هذا صحيحًا على الإطلاق. للانتقال إلى فرضية أكثر تعقيدًا (وغالبًا ما تكون أكثر استحسانًا) ، من الضروري ، استخدام بيانات الرصد ، لدحض الفرضية الأكثر بساطة والأكثر عمومية ، أو لتعزيزها والتخلي عن مزيد من التطوير للنظرية. الفرضية التي يتم اختبارها في كثير من الأحيان بهذه الطريقة تسمى باطل ، وهناك شعور عميق في هذا.

ما الذي يمكن أن يكون بمثابة فرضية فارغة؟ بمعنى ما ، أي شيء ، أي بيان ، ولكن بشرط أن يمكن ترجمته إلى لغة القياس. غالبًا ما تكون الفرضية هي القيمة المتوقعة لبعض المعلمات ، والتي تتحول إلى متغير عشوائي أثناء القياس ، أو عدم وجود اتصال (ارتباط) بين متغيرين عشوائيين. في بعض الأحيان يفترض نوع التوزيع ، عملية عشوائية ، يقترح بعض النماذج الرياضية. الصيغة الكلاسيكية للسؤال هي كما يلي: هل تسمح لنا الملاحظات برفض الفرضية الفارغة أم لا؟ بتعبير أدق ، مع اليقين الذي يمكن أن نقول أنه لا يمكن الحصول على الملاحظات على أساس فرضية لاغية؟ علاوة على ذلك ، إذا لم نتمكن من إثبات ، بناءً على بيانات إحصائية ، أن الفرضية الخاطئة خاطئة ، عندها تكون مقبولة.

وهنا قد تظن أن الباحثين مجبرون على ارتكاب أحد الأخطاء المنطقية الكلاسيكية ، والتي تحمل الاسم اللاتيني القديم الجاهل. هذه حجة حول حقيقة البيان ، بناءً على عدم وجود أدلة على زيفه. مثال كلاسيكي هو الكلمات التي قالها السيناتور جوزيف مكارثي عندما طُلب منه تقديم حقائق لدعم اتهامه بأن شخصًا ما شيوعيًا: "لدي القليل من المعلومات حول هذه المسألة ، باستثناء البيان العام للسلطات المختصة بأنه لا يوجد شيء في ملفه لاستبعاد علاقاته مع الشيوعيين " . أو حتى أكثر إشراقًا: "Bigfoot موجود ، لأنه لم يثبت أحد خلاف ذلك . " تحديد الفرق بين الفرضية العلمية والحيل المشابهة هو موضوع مجال الفلسفة بأكمله: منهجية المعرفة العلمية . أحد نتائجها المذهلة هي معيار القابلية للتزوير ، الذي طرحه الفيلسوف الرائع كارل بوبر في النصف الأول من القرن العشرين. تم تصميم هذا المعيار لفصل المعرفة العلمية عن غير علمي ، ويبدو للوهلة الأولى مفارقة:

لا يمكن اعتبار النظرية أو الفرضية علمية إلا إذا كانت هناك طريقة ، حتى من الناحية الافتراضية ، لدحضها.

ما ليس قانون الخسة! اتضح أن أي نظرية علمية غير صحيحة تلقائيًا ، ولا يمكن اعتبار النظرية الصحيحة "بحكم التعريف" علمية. علاوة على ذلك ، فإن العلوم مثل الرياضيات والمنطق لا تفي بهذا المعيار. ومع ذلك ، يتم إحالتها ليس إلى العلوم الطبيعية ، ولكن إلى العلوم الرسمية ، والتي لا تتطلب اختبارًا للتزوير. وإذا أضفنا نتيجة أخرى في نفس الوقت: مبدأ عدم اكتمال غودل ، والذي ينص على أنه من الممكن في أي نظام رسمي صياغة بيان لا يمكن إثباته أو دحضه ، فقد يصبح من غير الواضح سبب الانخراط في هذا العلم عمومًا. ومع ذلك ، من المهم أن نفهم أن مبدأ تزوير بوبر لا يقول أي شيء عن حقيقة النظرية ، ولكن فقط سواء كانت علمية أم لا. يمكن أن تساعد في تحديد ما إذا كانت النظرية تعطي لغة من المنطقي أن نتحدث فيها عن العالم أم لا.

ولكن لا يزال ، لماذا ، إذا لم نتمكن من رفض الفرضية على أساس البيانات الإحصائية ، فهل يحق لنا قبولها على أنها صحيحة؟ الحقيقة هي أن الفرضية الإحصائية ليست مأخوذة من رغبة أو تفضيلات الباحث ، بل يجب أن تتبع من أي قوانين رسمية عامة. على سبيل المثال ، من نظرية الحد المركزي ، أو من مبدأ الحد الأقصى للانتروبيا. تعكس هذه القوانين بشكل صحيح درجة جهلنا ، دون إضافة افتراضات أو فرضيات غير ضرورية. بمعنى ما ، هذا استخدام مباشر للمبدأ الفلسفي الشهير المعروف باسم شفرات أوكام :

ما يمكن القيام به على أساس عدد أقل من الافتراضات لا ينبغي أن يتم على أساس أكثر من ذلك.

وبالتالي ، عندما نقبل الفرضية الفارغة ، بناءً على عدم دحضها ، نظهر بشكل رسمي وصادق أنه نتيجة للتجربة ، بقيت درجة جهلنا على نفس المستوى . في مثال Bigfoot ، بشكل صريح أو ضمني ، يُفترض العكس: عدم وجود دليل على أن هذا المخلوق الغامض لا يبدو أنه شيء يمكن أن يزيد من درجة معرفتنا به.

بشكل عام ، من وجهة نظر مبدأ falsifiability ، أي بيان حول وجود شيء ما هو غير علمي ، لأن عدم وجود أدلة لا يثبت أي شيء. في الوقت نفسه ، يمكن دحض تأكيد عدم وجود أي شيء بسهولة من خلال توفير نسخة أو أدلة غير مباشرة أو عن طريق إثبات وجود البناء. وبهذا المعنى ، يحلل اختبار الفرضية الإحصائية مزاعم عدم وجود التأثير المطلوب ، ويمكن أن يقدم ، بطريقة ما ، دحضًا دقيقًا لهذا البيان. هذا هو بالضبط ما يبرره تمامًا مصطلح "فرضية لاغية": فهو يحتوي على الحد الأدنى الضروري من المعرفة حول النظام.

كيف تخلط بين الإحصائيات وكيف تنحل

من المهم للغاية التأكيد على أنه إذا كانت الإحصائيات تشير إلى أنه يمكن رفض الفرضية الفارغة ، فإن هذا لا يعني أننا أثبتنا بذلك حقيقة أي فرضية بديلة.يجب عدم الخلط بين الإحصائيات والمنطق ، فهناك مجموعة من الأخطاء الطفيفة ، خاصةً عندما تدخل الاحتمالات الشرطية للأحداث التابعة. على سبيل المثال: من غير المرجح أن يكون الشخص هو البابا ($$~ 1 / 7 مليار) متابعة من ذلك أن البابا يوحنا بولس الثاني لم يكن رجلا؟ يبدو البيان سخيفًا ، لكن لسوء الحظ ، مثل هذا الاستنتاج "الواضح" غير صحيح تمامًا: أظهر الاختبار أن اختبارًا متنقلًا لمحتوى الكحول في الدم لا يقدم المزيد$\sim 1/7$$$1 ٪ من كل من النتائج السلبية الإيجابية والخاطئة كاذبة ، لذلك ، في$1\%$$$98 ٪ من الحالات ، وقال انه يحدد بشكل صحيح سائق في حالة سكر. دعونا اختبار$98\%$$$1000 سائق ودع$1000$$$100 منهم سيكون في حالة سكر حقا. نتيجة لذلك ، نحصل عليه$100$$$900 × 1 ٪ = 9 كاذبة إيجابية و$900\times1\%=9$$$100 × 1 ٪ = 1 نتيجة سلبية كاذبة: أي بالنسبة إلى سكير واحد تسلل ، سيكون هناك تسعة سائقين عشوائيين متهمين ببراءة. ما ليس قانون الخسة! سيتم ملاحظة التكافؤ فقط إذا كانت نسبة السائقين في حالة سكر مساوية لـ$100\times1\%=1$$$$1/2$ , . , , !

. , : . , , . : .
يتم تعريف احتمال تقاطع الحدثين A و B على أنه ناتج احتمال وقوع الحدث B واحتمال الحدث $$A ، إذا كان من المعروف أن حدث قد حدث$A$$$$B$ :

$$

$$P(A \cap B) = P(B)P(A|B).$$

يمكنك الآن تحديد استقلال الأحداث بثلاث طرق متكافئة: الأحداث $$$A$ و $$ب مستقلة إذا$B$$$P ( A | B ) = P ( A ) ، أو$P(A|B) = P(A)$$$P ( B | A ) = P ( B ) ، أو$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ .
هذا يكمل التعريف الرسمي للاحتمال الذي بدأ في الفصل الأول.

التقاطع عملية تبادلية ، أي$$$P(A\cap B) = P(B\cap A)$ . تتبع نظرية بايز على الفور ما يلي:

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

والتي يمكن استخدامها لحساب الاحتمالات الشرطية.

في مثالنا مع السائقين واختبار الكحول ، لدينا أحداث:$$أ - السائق في حالة سكر ،$A$$$ب - أعطى الاختبار نتيجة إيجابية. الاحتمالات:$B$$$P ( A ) = 0.1 - احتمال أن يكون السائق الذي تم إيقافه في حالة سكر ؛$P(A) = 0.1$$$P ( B | A ) = 99 ٪ - احتمال أن يعطي الاختبار نتيجة إيجابية إذا كان من المعروف أن السائق في حالة سكر (مستبعد$P(B|A) = 99\%$$$1 ٪ سلبية كاذبة)$1\%$$$P ( A | B ) = 99 ٪ - احتمال أن يشرب الاختبار ، إذا أعطى الاختبار نتيجة إيجابية (مستبعد$P(A|B) = 99\%$$$1 نتائج إيجابية كاذبة). نحن نحسب$1%$$$$P (B)$ - احتمال الحصول على نتيجة اختبار إيجابية على الطريق:

$$

$$P (B) = \ frac {P (A) P (A | B)} {P (B | A)} = P (A) = 0.1$$

لقد أصبح تفكيرنا رسميًا ، وكما تعلمون ، ربما يكون ذلك لبعض الناس أكثر قابلية للفهم. يتيح لك مفهوم الاحتمال الشرطي التفكير المنطقي بلغة نظرية الاحتمالات. ليس من المستغرب أن تجد نظرية بايز تطبيقًا واسعًا في نظرية القرار ، وأنظمة التعرف على الأنماط ، وفلاتر البريد العشوائي ، والبرامج التي تختبر اختبارات الانتحال وفي العديد من تقنيات المعلومات الأخرى.

يتم فهم هذه الأمثلة بعناية من قبل الطلاب للاختبارات الطبية أو الممارسات القانونية. لكني أخشى ألا يتم تدريس الإحصائيات الرياضية أو نظرية الاحتمالات للصحفيين أو السياسيين ، لكنهم يروقون بشغف للبيانات الإحصائية ، ويفسرونها بحرية ويقدمون "المعرفة" المكتسبة للجماهير. لذلك ، أحث القارئ: لقد اكتشفت الرياضيات بنفسي ، وساعدني في معرفة ذلك من أجل شخص آخر! لا أرى أي ترياق آخر للجهل.

نقيس السذاجة لدينا

سننظر في تطبيق واحد فقط من الأساليب الإحصائية العديدة ونطبقه: اختبار الفرضيات الإحصائية. بالنسبة لأولئك الذين ربطوا حياتهم بالفعل بالعلوم الطبيعية أو الاجتماعية ، لن يكون هناك شيء جديد مذهل في هذه الأمثلة.

افترض أننا نقيس بشكل متكرر متغير عشوائي له قيمة متوسطة $$$\ mu$ والانحراف المعياري $$$\ سيجما$ . وفقًا لنظرية الحد المركزي ، سيتم توزيع القيمة المتوسطة المرصودة بشكل طبيعي. من قانون الأعداد الكبيرة يترتب على ذلك أن متوسطها سوف يميل إلى $$$\ mu$ ومن خصائص التوزيع الطبيعي يتبع ذلك بعد $$$ن$ القياس ، التباين الملحوظ من المتوسط ​​سينخفض $$$\ sigma / \ sqrt {n}$ . يمكن اعتبار الانحراف المعياري هو الخطأ المطلق للقياس المتوسط ​​، وسيكون الخطأ النسبي في هذه الحالة مساوياً $$$\ delta = \ sigma / (\ sqrt {n} \ mu)$ . هذه استنتاجات عامة جدًا ، مستقلة عن الحجم الكافي $$$ن$ من شكل التوزيع المحدد للمتغير العشوائي الذي تم التحقيق فيه. هناك قاعدتان مفيدتان (وليس القوانين) تتبعهما:

1. الحد الأدنى لعدد الاختبارات $$$ن$ يجب أن تمليها الخطأ النسبي المطلوب $$$\ دلتا$ . علاوة على ذلك ، إذا

$$

$$n \ geq \ left (\ frac {2 \ sigma} {\ mu \ delta} \ right) ^ 2 ،$$

ثم احتمال بقاء المتوسط ​​المرصود ضمن الخطأ المحدد سيكون على الأقل $$ . في $$$\ mu$ بالقرب من الصفر ، والخطأ النسبي هو الأفضل ليحل محل المطلق.

2. دع الفرضية هي الفرضية الفارغة التي تشير إلى أن الوسط الملحوظ هو $$$\ mu$ . ثم ، إذا كان المتوسط ​​المرصود لا يتجاوز $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ ، ثم احتمال أن تكون الفرضية صحيحة صحيحة ستكون على الأقل $$ .


إذا تم استبدالها في هذه القواعد $$$2 \ سيجما$ على $$$3 \ سيجما$ ثم درجة الثقة ستزداد $$ هذه قاعدة قوية جدا $$$3 \ سيجما$ ، والتي في العلوم الفيزيائية تفصل الافتراضات عن حقيقة ثابتة تجريبيا.

سيكون من المفيد لنا أن نفكر في تطبيق هذه القواعد على توزيع Bernoulli الذي يصف متغيرًا عشوائيًا يأخذ قيمتين تمامًا ، يطلق عليهما "النجاح" و "الفشل" ، مع وجود احتمال معين للنجاح $$$ع$ . في هذه الحالة $$$\ mu = p$ و $$$\ sigma = \ sqrt {p (1-p)}$ ، لذلك بالنسبة للعدد المطلوب من التجارب وفترة الثقة التي نحصل عليها

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad و \ quad np \ pm 2 \ sqrt {np (1-p)}.$$

القاعدة $$$2 \ سيجما$ يمكن استخدام توزيع برنولي لتحديد الفاصل الزمني للثقة عند رسم الرسوم البيانية. في الأساس ، يمثل كل شريط في الرسم البياني متغيرًا عشوائيًا ذا قيمتين: "hit" - "missed" ، حيث يتوافق احتمال الضرب مع دالة احتمال محاكية. كإجراء توضيحي ، سنقوم بإنشاء العديد من العينات لثلاثة توزيعات: موحدة ، هندسية ، وعادية ، وبعد ذلك نقوم بمقارنة تقديرات الانتثار للبيانات المرصودة مع الانتثار الملحوظ. وهنا نرى مرة أخرى أصداء نظرية الحد المركزي ، التي تتجلى في حقيقة أن توزيع البيانات حول القيم المتوسطة في الرسم البياني يقترب من المعدل الطبيعي. ومع ذلك ، بالقرب من الصفر يصبح الفارق غير متماثل ويقترب من التوزيع المحتمل للغاية - الأسي. يوضح هذا المثال جيدًا ما قصدته بالقول إننا في الإحصائيات نتعامل مع قيم عشوائية لمعلمات متغير عشوائي.


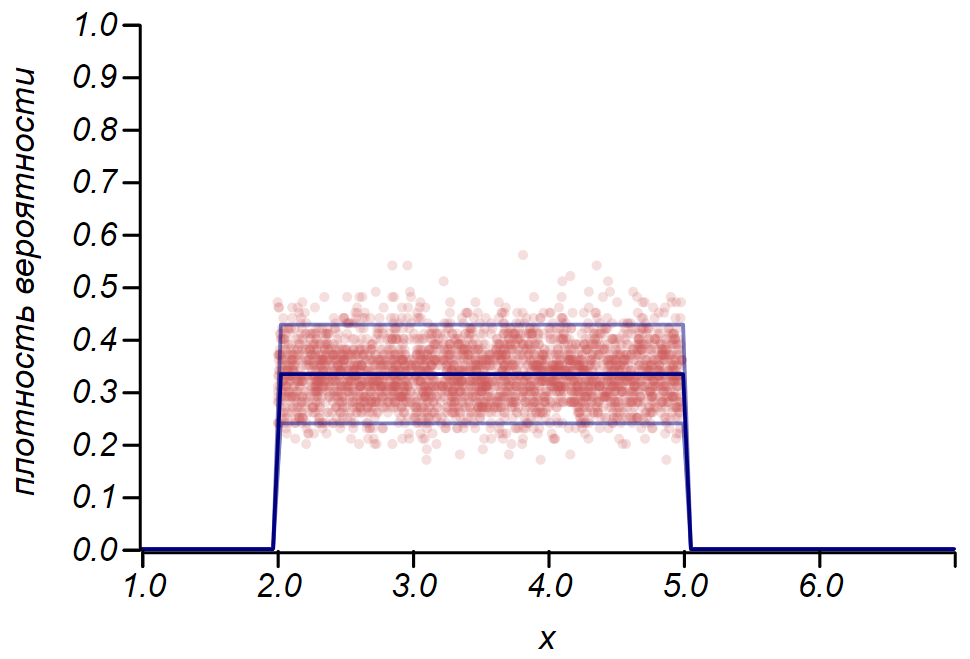
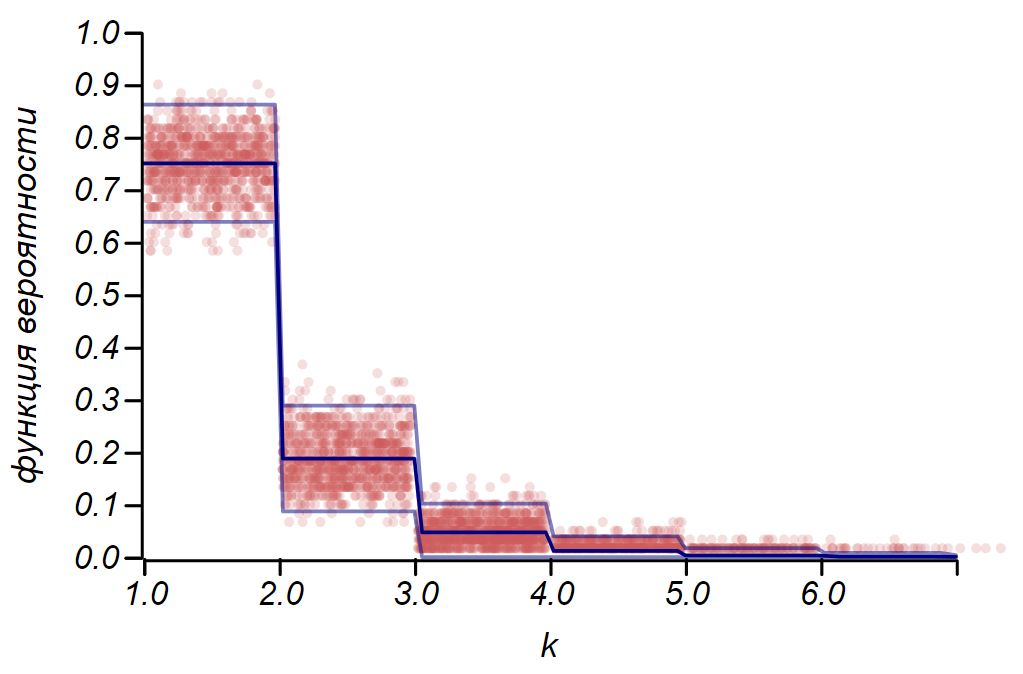مثال يوضح نسبة التقديرات المبعثرة الصادرة عن القاعدة $$$2 \ سيجما$ وانتشار لوحظ لثلاثة متغيرات عشوائية.

من المهم أن نفهم أن القواعد $$$2 \ سيجما$ و حتى $$$3 \ سيجما$ لا تنقذنا من الأخطاء. أنها لا تضمن حقيقة أي بيان ، ليست أدلة. الإحصاءات تحد من درجة عدم الثقة في الفرضية ، ولا شيء أكثر من ذلك.

قدم عالم الرياضيات ومؤلف دورة ممتازة في نظرية الاحتمالات ، جيان كارلو روتا ، مثالاً في محاضراته في معهد ماساتشوستس للتكنولوجيا. تخيل مجلة علمية اتخذ محرراها قرارًا قويًا: قبول المقالات المنشورة حصريًا مع نتائج إيجابية ترضي القاعدة $$$2 \ سيجما$ أو أكثر صرامة. في الوقت نفسه ، يشير عمود التحرير إلى أن القراء يمكن أن يكونوا متأكدين من احتمال حدوث ذلك $$ لن يجد القارئ النتيجة الخاطئة على صفحات هذه المجلة! للأسف ، يمكن دحض هذا البيان بسهولة بنفس المنطق الذي أدى بنا إلى الظلم الفاضح عند اختبار السائقين للكحول. هيا $$ الباحثين ذوي الخبرة $$ الفرضيات ، التي جزء منها صحيح فقط ، يقول ، $$$10 \٪$ . بناءً على معنى اختبار الفرضيات ، يمكننا توقع ذلك $$ لن يتم رفض الافتراضات غير الصحيحة عن طريق الخطأ ، وسيتم تسجيل الدخول معها $$ نتائج حقيقية. مجموع $$ جيد ثالث سيكون خطأ!

يوضح هذا المثال تمامًا قانوننا الداخلي للخلاص ، والذي لم يتم تضمينه بعد في مختارات علم التشكل ، قانون تشيرنوميردين :

أردنا الأفضل ، لكن اتضح ، كما هو الحال دائمًا.

من السهل الحصول على تقدير عام لنسبة النتائج غير الصحيحة التي سيتم تضمينها في أعداد المجلة ، على افتراض أن حصة الفرضيات الحقيقية هي $$$0 <\ alpha <1$ واحتمال قبول فرضية خاطئة يساوي $$$ع$ :

$$

$$x = \ frac {(1- \ alpha) p} {\ alpha (1-p) + (1- \ alpha) p}.$$

يتم عرض المجالات التي تحد من حصة النتائج غير الصحيحة عن عمد والتي يمكن نشرها في المجلة في الشكل.

تقدير النسبة المئوية للمنشورات التي تحتوي على نتائج غير صحيحة بوضوح عند اعتماد معايير مختلفة لاختبار الفرضيات يمكن أن نرى أن قبول الفرضيات حسب القاعدة $$$2 \ سيجما$ يمكن أن تكون محفوفة بالمخاطر في حين أن المعيار $$$4 \ سيجما$ يمكن بالفعل أن تعتبر قوية جدا.

بالطبع نحن لا نعرف هذا. $$$\ alpha$ ، ولن نعرف أبدًا ، لكنها بالتأكيد أقل من الوحدة ، مما يعني أنه في أي حال ، لا يمكن أخذ البيان من عمود التحرير على محمل الجد. يمكنك قصر نفسك على معايير صارمة $$$4 \ سيجما$ لكنه يتطلب عددًا كبيرًا جدًا من الاختبارات. لذلك ، من الضروري زيادة حصة الفرضيات الحقيقية في مجموعة الافتراضات المحتملة. تهدف المناهج القياسية للطريقة العلمية للإدراك إلى هذا - الاتساق المنطقي للفرضيات ، وتوافقها مع الحقائق والنظريات التي أثبتت قابليتها للتطبيق ، والاعتماد على النماذج الرياضية والتفكير النقدي.

ومرة أخرى عن الطقس

في بداية الفصل ، تحدثنا عن حقيقة أن عطلة نهاية الأسبوع والطقس السيئ يتزامن في كثير من الأحيان أكثر مما نود. دعنا نحاول إكمال هذه الدراسة. يمكن اعتبار كل يوم ممطر بمثابة ملاحظة لمتغير عشوائي - يوم الأسبوع الذي يطيع توزيع برنولي مع احتمال $$ . دعنا نفترض ، كفرضية لاغية ، أن افتراض أن جميع أيام الأسبوع هي نفسها من حيث الطقس والمطر يمكن أن تمطر في أي منها على الأرجح. لدينا عطلة لمدة يومين ، لذلك نحصل على الاحتمال المتوقع لمصادفة يوم سيء ويوم عطلة متساوٍ $$ ، ستكون هذه القيمة معلمة التوزيع Bernoulli. كم مرة تمطر؟ في أوقات مختلفة من العام ، بطرق مختلفة ، بالطبع ، ولكن في بيتروبافلوفسك كامتشاتسكي ، في المتوسط ​​، هناك تسعون يومًا ممطرًا أو ثلجيًا في السنة. لذلك تيار الأيام مع هطول الأمطار لديه كثافة حوالي $$$90/365 \ approx1 / 4$ . دعونا نحسب عدد عطلات نهاية الأسبوع الممطرة التي يجب أن نسجلها للتأكد من وجود نمط ما. يتم عرض النتائج في الجدول.

فترة المراقبة	الصيف	سنة	$$ سنوات
العدد المتوقع من الملاحظات	$$	$$	$$
العدد المتوقع للنتائج الإيجابية	$$	$$	$$
انحراف كبير	$$	$$	$$
نسبة كبيرة من السيئة إجمالي عدد أيام العطلة	$$$42 \٪$	$$	$$

عن ماذا تتحدث هذه الأرقام؟ إذا بدا لك أنه لم يكن هناك "صيف" لمدة عام على التوالي ، فإن الصخرة الشريرة تطارد عطلة نهاية الأسبوع عن طريق إرسال المطر إليهم ، ويمكن التحقق من ذلك وتأكيده. ومع ذلك ، خلال فصل الصيف ، لا يمكن اكتشاف الصخرة الشريرة إلا إذا كان أكثر من خُمس عطلة نهاية الأسبوع ممطرة. تشير الفرضية الفارغة إلى أن ربع عطلة نهاية الأسبوع فقط يجب أن يتزامن مع طقس عاصف. خلال خمس سنوات من الملاحظة ، يمكن للمرء بالفعل أن يأمل أن يلاحظ انحرافات خفية تتجاوز ذلك $$$5 \٪$ وإذا لزم الأمر ، تابع شرحهم.

استفدت من مذكرات الطقس المدرسي ، التي أجريت في الفترة من 2014 إلى 2018 ، واكتشفت ما حدث خلال هذه السنوات الخمس $$ الأيام الممطرة منهم $$ سقط في عطلة نهاية الأسبوع. هذا ، في الواقع ، أكثر من الرقم المتوقع من قبل $$ أيام ، ولكن الانحرافات الكبيرة تبدأ $$ أيام ، لذلك هذا ، كما قلنا في الطفولة: "لا يهم". فيما يلي سلسلة من البيانات ورسم بياني يوضح توزيع الطقس السيئ حسب يوم الأسبوع. تشير الخطوط الأفقية في الرسم البياني إلى الفاصل الزمني الذي يمكن فيه ملاحظة انحراف عشوائي عن التوزيع الموحد لنفس كمية البيانات.


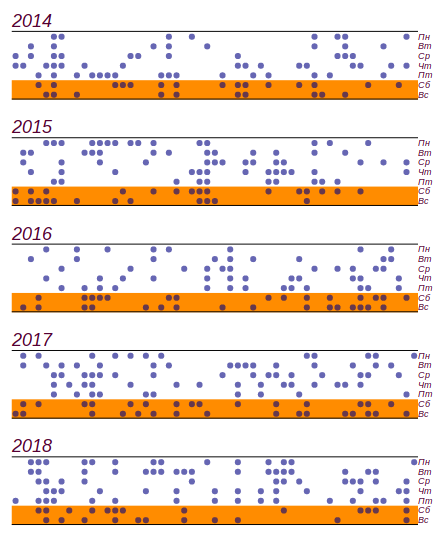
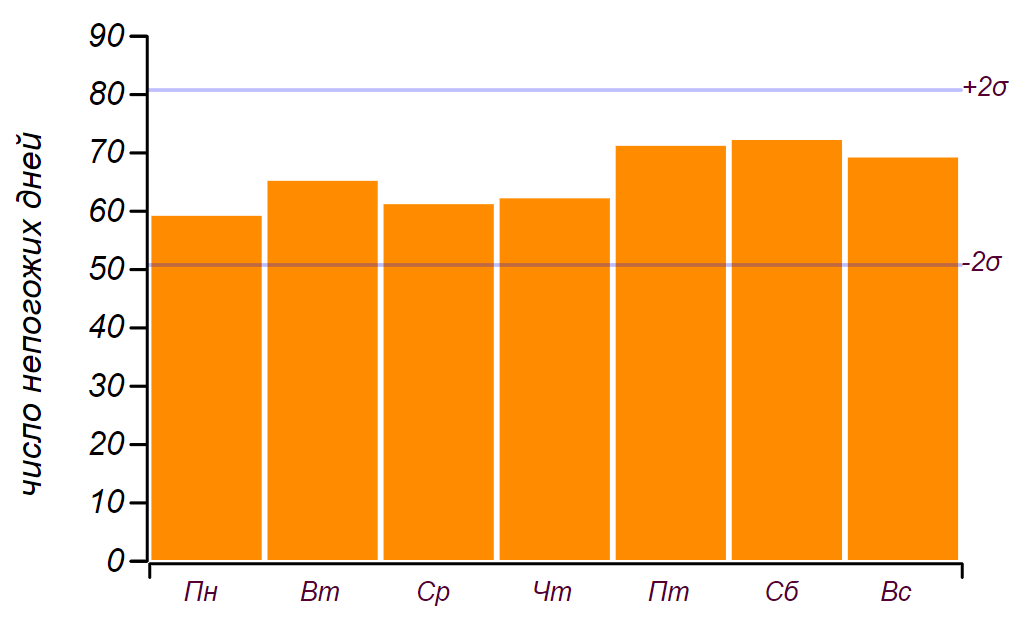تم الحصول على سلسلة البيانات الأولية وتوزيع الأيام السيئة حسب أيام الأسبوع على مدار خمس سنوات من المراقبة.

يمكن أن نرى أنه منذ يوم الجمعة ، في الواقع ، كانت هناك زيادة في عدد الأيام بسبب سوء الاحوال الجوية. لكن الشروط المسبقة ليست كافية لإيجاد سبب لهذا النمو: يمكن الحصول على نفس النتيجة ببساطة عن طريق الفرز بأرقام عشوائية. الخلاصة: على مدى خمس سنوات من مراقبة الطقس ، جمعت ما يقرب من ألفي سجل ، لكنني لم أتعلم شيئًا جديدًا حول توزيع الطقس بحلول أيام الأسبوع.

عندما تنظر إلى المذكرات اليومية ، من الواضح أن الطقس لا يأتي بمفرده ، ولكن في فترات من يومين إلى ثلاثة أيام أو حتى الأعاصير الأسبوعية. هل هذا يؤثر بطريقة ما على النتيجة؟ يمكنك محاولة أخذ هذه الملاحظة في الاعتبار ، وافتراض أنها تمطر في المتوسط ​​لمدة يومين (في الواقع ، $$ أيام) ، ثم يزيد احتمال حظر عطلة نهاية الأسبوع إلى $$ . في ظل هذا الاحتمال ، يجب أن يكون العدد المتوقع للمباريات لمدة خمس سنوات $$ ، أي من $$ قبل $$ مرات. القيمة الملحوظة $$ لا يقع في هذا النطاق ، وبالتالي ، يمكن رفض فرضية تأثير الأيام المزدوجة لسوء الأحوال الجوية بأمان. هل تعلمنا شيئا جديدا؟ نعم ، لقد تعلمنا: يبدو أن ميزة واضحة للعملية لا تنطوي على أي تأثير. هذا يستحق الدراسة ، وسنفعل ذلك لاحقًا. لكن الاستنتاج الرئيسي هو أنه لا توجد أسباب للنظر في أي آثار أكثر دقة ، لأن الملاحظات ، والأهم من ذلك ، تتحدث باستمرار لصالح أبسط تفسير.

لكن استيائنا ليس إحصاءات مدتها خمس سنوات أو حتى إحصاءات سنوية ، فذاكرة الإنسان ليست طويلة. إنه لأمر مخز عندما تمطر في عطلة نهاية الأسبوع ثلاث أو أربع مرات على التوالي! كم مرة يمكن ملاحظة ذلك؟ خاصة إذا كنت تتذكر أن الطقس السيئ لا يأتي بمفرده. يمكن صياغة المهمة على النحو التالي: "ما هو احتمال ذلك $$$ن$ عطلة نهاية الأسبوع على التوالي ستكون ممطرة؟ " من المعقول افتراض أن الطقس السيئ يشكل تيار Poisson بكثافة $$ . هذا يعني أنه في المتوسط ​​، سيكون ربع أيام أي فترة سيئًا. في مراقبة عطلة نهاية الأسبوع فقط ، يجب ألا نغير كثافة التدفق ، وفي كل عطلة نهاية الأسبوع ، يجب أن يكون الطقس السيئ ، في المتوسط ​​، أيضًا ربع. لذلك ، طرحنا الفرضية الفارغة: دفق الطقس السيئ هو Poisson ، مع معلمة معروفة ، مما يعني أن الفواصل الزمنية بين أحداث Poisson يتم وصفها بواسطة التوزيع الأسي. نحن مهتمون بفواصل زمنية منفصلة: $$$0 ، \ 1 ، \ 2 ، \ 3 دولا$ أيام ، وما إلى ذلك وبالتالي يمكننا استخدام التناظرية المنفصلة للتوزيع الأسي - التوزيع الهندسي مع المعلمة $$ . يوضح الشكل ما فعلناه ويمكن ملاحظة أن الافتراض بأننا نراقب عملية بواسون ليس من المنطقي رفضه.


التوزيع الملحوظ لطول سلاسل نهاية الأسبوع الفاشلة والنظرية. يُظهر الخط الرفيع الانحرافات المسموح بها لعدد المشاهدات التي لدينا.

يمكنك أن تسأل نفسك هذا السؤال: كم سنة تحتاج إلى إبداء ملاحظات حتى يكون الاختلاف فيها $$ يمكن تأكيد الأيام أو بثبات بانحراف عشوائي؟ من السهل حسابها: الاحتمال الملحوظ $$ يختلف عن المتوقع $$ على $$ . لتسجيل الاختلافات في المئات ، خطأ مطلق لا يزيد عن $$ هذا يجعل $$ من الحجم المقاس. من هنا نحصل على حجم العينة المطلوب $$$n \ geq (4 \ cdot 5/7) / (0.0175 ^ 2 \ cdot 2/7) \ 32000 دولار تقريبً$ أيام ممطرة. سوف يستغرق حوالي $$$4 \ cdot 32000/365 \ approx 360$ سنوات من الأرصاد الجوية المستمرة ، لأنه كل يوم رابع فقط تمطر أو ثلج. للأسف ، هذا هو أكثر من الوقت الذي تكون فيه كامتشاتكا جزءًا من روسيا ، لذلك ليس لدي فرصة لمعرفة كيف تكون الأمور "حقًا". لا سيما إذا كنت تأخذ في الاعتبار أنه خلال هذا الوقت تمكن المناخ من التغيير بشكل كبير - من العصر الجليدي الصغير ، خرجت الطبيعة بالطريقة المثلى التالية.

فكيف تمكن الباحثون الأستراليون من تسجيل انحراف درجات الحرارة في كسور الدرجة ولماذا من المنطقي التفكير في هذه الدراسة؟ الحقيقة هي أنهم استخدموا بيانات درجة الحرارة للساعة التي لم يتم "تخفيفها" بواسطة أي عملية عشوائية. بعد ذلك $$ سنوات من الأرصاد الجوية تمكنت من تجميع أكثر من ربع مليون قراءات ، مما يسمح للحد من الانحراف المعياري للمتوسط $$ مرات فيما يتعلق بانحراف درجة الحرارة اليومية القياسية. هذا يكفي للحديث عن الدقة في أعشار الدرجة. بالإضافة إلى ذلك ، استخدم المؤلفون طريقة جميلة أخرى تؤكد وجود دورة زمنية: الاختلاط العشوائي للسلسلة الزمنية. يحافظ هذا الخلط على الخصائص الإحصائية ، مثل كثافة التدفق ، لكنه "يمحو" الأنماط الزمنية ، مما يجعل العملية Poisson حقيقية. تسمح لنا مقارنة العديد من المسلسلات التجريبية والتركيبية بالتحقق من أن الانحرافات الملحوظة للعملية من Poisson مهمة. بالطريقة نفسها ، أظهر عالم الزلازل أ. أ. غوسيف أن الزلازل في أي منطقة تشكل نوعًا من التدفق المتشابه ذاتيا مع خصائص التجميع. وهذا يعني أن الزلازل تميل إلى التجمع في الوقت المناسب ، وتشكيل الأختام تدفق غير سارة للغاية. في وقت لاحق اتضح أن تسلسل الانفجارات البركانية الكبيرة له نفس الخاصية.

مصدر آخر للعشوائية

بالطبع ، لا يمكن وصف الطقس ، مثل الزلازل ، بعملية بواسون - فهذه عمليات ديناميكية تكون فيها الحالة الحالية دالة على العمليات السابقة. لماذا ملاحظات الطقس الأسبوعية لدينا تفضل نموذج عشوائي بسيط؟ والحقيقة هي أننا نعرض العملية المعتادة لتشكيل الهطول لمدة سبعة أيام ، أو عند التحدث بلغة الرياضيات ، على نظام الخصومات modulo seven . عملية الإسقاط هذه قادرة على توليد الفوضى من سلسلة من البيانات جيدة التنظيم. من هنا ، على سبيل المثال ، هناك عشوائية عشوائية في تسلسل أرقام العلامة العشرية لمعظم الأرقام الحقيقية.

لقد تحدثنا بالفعل عن الأرقام المنطقية ، تلك المعبر عنها كسور عدد صحيح. لديهم بنية داخلية ، يتم تحديدها من خلال رقمين: البسط والمقام. ولكن عند الكتابة في شكل عشري ، يمكنك ملاحظة قفزات من الانتظام في تمثيل الأرقام مثل $$$1/2 = 0.5 \ overline {0}$ أو $$$1/3 = 0. \ Overline {3}$ إلى التكرار الدوري لسلسلة عشوائية بالفعل في أرقام مثل $$ . لا تحتوي الأرقام غير المنطقية على علامة عشرية محددة أو دورية ، وفي هذه الحالة ، تسود الفوضى في معظم الأحيان في سلسلة من الأرقام. ولكن هذا لا يعني أنه لا يوجد ترتيب في هذه الأرقام! على سبيل المثال ، أول عدد غير عقلاني واجهه علماء الرياضيات $$$\ sqrt {2}$ في التدوين العشري يولد مجموعة عشوائية من الأرقام. ومع ذلك ، من ناحية أخرى ، يمكن تمثيل هذا الرقم ككسر مستمر لانهائي:

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}.$$

من السهل إظهار أن هذه السلسلة تساوي بالفعل جذر اثنين عن طريق حل المعادلة:

$$

$$x-1 = \ frac {1} {2+ (x-1)}.$$

تتم كتابة الكسور المستمرة ذات المعاملات المتكررة قريبًا ، مثل الكسور العشرية الدورية ، على سبيل المثال: $$$\ sqrt {2} = [1 ، \ bar {2}]$ ، $$$\ sqrt {3} = [1 ، \ overline {1،2}]$ . النسبة الذهبية المشهورة بهذا المعنى هي الرقم غير المنطقي الأكثر ترتيبًا: $$$\ varphi = [1، \ bar {1}]$ . يتم تمثيل جميع الأرقام المنطقية في شكل كسور مستمرة محدودة ، وبعضها غير عقلاني - في شكل لانهائي ، ولكن دوري ، يطلق عليها اسم جبري ، وهو نفس الشيء الذي لا يحتوي على تدوين محدود حتى في هذا الشكل - متجاوز . الاكثر شهرة من المتسامي هو الرقم $$$\ pi$ ، فإنه يخلق الفوضى في كل من العشري وفي شكل كسر مستمر: $$$\ pi \ approx [3، 7،15،1،292،1،1،1،2،1،3،1،14،2،1، ...]$ . وهنا رقم أويلر $$$e$ الباقي المتسامي ، في شكل كسر مستمر ، يعرض البنية الداخلية المخفية في العلامة العشرية: $$$e \ approx [2،1،2،1،1،4،1،1،6،1،1،8،1،1،10، ...]$ .

ربما لم يشك عالم رياضيات واحد ، بدءاً من فيثاغورس ، في عالم الماكرة ، واكتشاف ما هو مطلوب ، مثل هذا الرقم الأساسي $$ ع لدي مثل هذا الهيكل الفوضوي معقدة بعيد المنال. بالطبع ، يمكن تمثيلها على أنها سلسلة من السلاسل العددية الأنيقة تمامًا ، ولكن هذه السلسلة لا تتحدث مباشرة عن طبيعة هذا الرقم وليست عالمية. أعتقد أن علماء الرياضيات في المستقبل سوف يكتشفون بعض التمثيل الجديد للأرقام ، وهو عالمي مثل الكسور المستمرة ، والتي سوف تكشف عن الترتيب الصارم الذي تخفيه الطبيعة بالأرقام.$\ pi$

$$

$$*\ *\ *$$

نتائج هذا الفصل ، في معظمها ، سلبية. وبصفتي مؤلفًا يريد أن يفاجئ القارئ بأنماط مخفية واكتشافات غير متوقعة ، فقد شككت في ضرورة تضمينه في الكتاب. لكن حديثنا عن الطقس ذهب إلى موضوع مهم للغاية - قيمة ودلالة نهج العلوم الطبيعية.

فتاة واحدة حكيمة ، وهي سونيا شاتالوفا ، التي تنظر إلى العالم من خلال منظور التوحد ، في سن العاشرة قدمت تعريفًا دقيقًا ودقيقًا: "العلم هو نظام معرفة قائم على الشك". العالم الحقيقي غير مستقر ويسعى جاهداً للاختباء وراء التعقيد والعشوائية المرئية وعدم موثوقية القياسات. شك في العلوم الطبيعية أمر لا مفر منه. يبدو أن الرياضيات عالم من اليقين ، والذي ، على ما يبدو ، يمكن للمرء أن ينسى الشك. ومن المغري أن نختبئ خلف جدران هذه المملكة. النظر في نماذج العالم التي لا يمكن التعرف عليها والتي يمكن التحقيق فيها بدقة ؛ حساب وحساب ، الاستفادة من الصيغة جاهزة لهضم أي شيء. لكن مع ذلك ، تعتبر الرياضيات علمًا ومما لا شك فيه أنها صدق داخلي عميق لا يعطي الراحة حتى يتم مسح البناء الرياضي من افتراضات إضافية وافتراضات غير ضرورية. في عالم الرياضيات ، يتحدثون لغة معقدة ، ولكن متناغمة ، ومناسبة للتفكير في العالم الحقيقي. من المهم للغاية التعرف على هذه اللغة قليلاً ،من أجل منع الشخصيات من انتحال الإحصاءات ، وعدم السماح للحقائق بالتظاهر بأنها المعرفة ، والجهل والتلاعب يتناقضان مع العلم الحقيقي.