مليار مشكلة مشكلة أو "دراسة الأنماط في قائمة حلول مشكلة توزيع n-Queens"

ملخص

ويرد وصف للقوانين التي وضعت في قائمة متسلسلة لجميع الحلول لمشكلة توزيع n-Queens. ثبت أن:

• تنخفض نسبة الحلول الكاملة في القائمة العامة لجميع الحلول ، مع زيادة قيمة n.
  
• يتم توزيع الحلول الكاملة في قائمة متسلسلة من جميع الحلول بطريقة من المرجح أن يتم العثور على الحلول الكاملة الموجودة بالقرب من بعضها البعض في القائمة.
  
• هناك تناظر في ترتيب الحلول الكاملة في القائمة العامة لجميع الحلول. في حالة اكتمال الحل في الموضع رقم i من بداية القائمة ، يكون الحل المتماثل من نهاية القائمة في الموضع n-i + 1 كاملاً أيضًا (قاعدة تماثل الحلول).
  
• أي أزواج من الحلول ، سواء أكانت قصيرة أم كاملة ، موجودة بشكل متماثل في قائمة جميع الحلول ، تكاملية - مجموع مؤشرات موضع الخطوط المتوافقة ثابت ومساوي لـ n + 1 (قاعدة تكامل الحلول). يشير هذا إلى أن النصف الأول فقط من قائمة جميع الحلول الكاملة هو "فريد" ، ويمكن الحصول على أي حل كامل من النصف الثاني من القائمة على أساس قاعدة التكامل. نتيجة هذه القاعدة هي حقيقة أنه بالنسبة لأي قيمة لـ n ، فإن عدد الحلول الكاملة سيكون دائمًا رقم زوجي.
  
• نشاط خلايا صفوف المصفوفة الحل متماثل فيما يتعلق بالمحور الأفقي الذي يمر عبر منتصف هذه المصفوفة. هذا يعني أن نشاط خلايا الصف الأول يتزامن دائمًا مع نشاط خلايا الصف n-i + 1. حسب النشاط يعني التردد الذي يحدث به مؤشر الخلية في السطر المقابل من قائمة الحلول الكاملة. وبالمثل ، فإن نشاط خلايا أعمدة المصفوفة الحل متماثل حول المحور العمودي الذي يقسم المصفوفة إلى جزأين متساويين
  
• بغض النظر عن n ، في البحث المتتالي لجميع الحلول ، لا يظهر الحل الكامل الأول إلا بعد سلسلة معينة من الحلول القصيرة. يزيد حجم التسلسل الأولي للحلول القصيرة مع n. يعد طول قائمة الحلول القصيرة قبل ظهور أول حل كامل للقيم الزوجية n أطول بكثير من أقرب القيم الفردية.
  
• الخط في مصفوفة القرار ، والتي تبدأ الصعوبات في المضي قدمًا ، ويتم تشكيل القرار القصير الأول ، يقسم المصفوفة وفقًا لقاعدة النسبة الذهبية. بالنسبة للقيم الصغيرة لـ n ، يكون هذا الاستنتاج تقريبيًا ، ومع زيادة في قيمة n ، تزداد دقة مثل هذا الاستنتاج بشكل مقارب إلى مستوى القاعدة القياسية.
  

يعرض هذا المنشور النتائج الرئيسية للمقالة [1] ، التي نشرت في مجلة "نمذجة الذكاء الاصطناعي ، 2018 ، 5 (1)". على Habré كانت هناك أعمال مرتبطة بمشكلة n-Queens: [2] ، [3] ،
مشكلة توزيع ملكات n على رقعة الشطرنج بحجم nxn لها تاريخ طويل. صُمم في الأصل في عام 1848 بواسطة M. Bezzel [4] كمهمة فكرية لشطرنج رقائقي منتظم. بمرور الوقت ، تم توسيع بيان المشكلة عن طريق F. Nauck [5] ، ويمكن أن يتخذ حجم رقعة الشطرنج أي قيمة.

مقدمة

بيان المشكلة بسيط للغاية: تحتاج إلى توزيع ملكات n على رقعة شطرنج بحجم nxn بحيث لا يوجد أكثر من ملكة واحدة في كل صف وفي كل عمود وكذلك على الأقطار اليسرى واليمنى التي تمر عبر الخلية حيث توجد الملكة. من السهل فهم هذه المهمة أو شرحها لشخص ما ، ولكن من الصعب حلها. الحقيقة هي أنه لا توجد قواعد يمكنك على أساسها ترتيب الملكات على كل سطر حتى تحصل على حل. يمكن الحصول على الحل فقط عن طريق تعداد المتغيرات المختلفة لترتيب الملكات في خطوط معينة. ومع ذلك ، يكمن تعقيد طريقة الحل هذه في حقيقة أن عدد كل المتغيرات لترتيب الملكات يزداد باطراد مع زيادة n. بالإضافة إلى ذلك ، يؤدي اتخاذ أي خطوة إلى الأمام لوضع الملكة في الموضع الحر لخط معين إلى تغيير في قائمة المواقف المجانية في الأسطر المتبقية ، وعند العودة خطوة واحدة ، من أجل تشكيل فرع البحث ، من الضروري مسح آثار الإجراءات التي تم تنفيذها مسبقًا.

هناك عدد كبير من المنشورات المتعلقة بجوانب مختلفة لحل مشكلة n-Queens. يمكن عزوها إلى العديد من مجالات البحث: البحث عن جميع الحلول الكاملة لقيمة معينة بحجم رقعة الشطرنج (n) ، تطوير خوارزمية سريعة لإيجاد حل واحد لقيم مختلفة من n ، حل المشكلة الكاملة إلى حل كامل ، لتكوين تعسفي للملكات k ، أسئلة التعقيد الحسابي للحسابات الخوارزمية ، وكذلك التعديلات المختلفة للصياغة الأصلية للمشكلة. للتعرف على هذه المجالات ، أود أن أوصي بمنشورات مثيرة للاهتمام من قبل B. Jordan و S. Brett [6] و IP Gent، C. Jefferson، P. Nightingale [7] ، والتي تقدم لمحة مفصلة إلى حد ما عن مجالات البحث المختلفة. تجدر الإشارة بشكل خاص إلى منشور الإنترنت [8] بدعم من Walter Costers ، والذي أعدته مجموعة من Universiteit Leiden ويحتوي على روابط إلى 342 منشورًا يتعلق بمشكلة n-queens (اعتبارًا من ديسمبر 2018).

على الرغم من أن مشكلة n-Queens ظلت نشطة لأكثر من 150 عامًا ، وقد ظهر عدد كبير من المنشورات خلال هذا الوقت ، لم أجد وظيفة ذات صلة بالبحث عن أنماط في نتائج حل هذه المشكلة. على الأرجح أن معظم المشاريع المتعلقة بالبحث عن جميع الحلول لم تحفظ الحلول التي تم العثور عليها ولم تر ما كان "في الداخل" ، وفي بيان المشكلة كانت هناك أهداف مهيمنة أخرى ، وقد حققها زملاؤنا الكرام. ومع ذلك ، بدا لي أن الوضع مشابه عن بعد عندما يتغلى الشخص بالبيض لتناول الإفطار ، لكنه لا يأكلها ، ولكنه يرميها بعيدًا ، ويترك فقط عدد البيض المسلوق في ذاكرته. كنت دائمًا على يقين من أنه إذا لم تكن البيانات عشوائية ، فيجب أن يكون هناك انتظام معين ، حتى لو لم نتمكن من العثور على هذا الانتظام. كان هذا الاقتناع هو السبب في البحث عن الأنماط في هذه المهمة.

إلى جانب الرغبة في تزويد أعضاء مجتمع Habr بمعلومات مفيدة عن التفكير ، أود أن المبرمجين الموهوبين ، ومعظمهم على Habr ، إيلاء المزيد من الاهتمام لمثل هذا الاتجاه من التنمية مثل محاكاة الكمبيوتر (المحاكاة الحاسوبية). كأسلوب بحثي ، يتم استخدام "الرياضيات الخوارزمية" في "الحافة الرائدة" في العديد من المجالات: الذكاء الاصطناعي ، علوم البرمجيات ، علوم البيانات ، ... وأنا متأكد من أن المشاكل المعقدة والهامة للغاية للتطبيق العملي سيتم حلها على أساس الرياضيات الخوارزمية خلاف ذلك.

تعاريف

فيما يلي ، سنشير إلى حجم رقعة الشطرنج بالرمز n. سيتم استدعاء حل كامل إذا تم وضع جميع ملكات n باستمرار على رقعة الشطرنج. جميع الحلول الأخرى ، عندما يكون عدد الملكات الموضوعة بشكل صحيح أقل من n - سوف نسميها حلولاً قصيرة. بطول الحل ، نعني عدد (k) للملكات الموضوعة بشكل صحيح. سيتم الإشارة إلى عدد كل الحلول ، بقيمة معينة من n ، ب m. كتناظرية لـ "رقعة الشطرنج" بحجم nx n. ، سننظر في "مصفوفة حل" بحجم nx n.

ابدأ

من أجل إجراء دراسة ، تم تطوير خوارزمية للبحث عن جميع الحلول للحصول على قيمة تعسفية لـ n. لم نستخدم العودية القياسية أو النظام المعتاد للحلقات المتداخلة. لقيم كبيرة من ن ، مثل هذا النهج سيكون إشكالية للغاية. تم بناء الخوارزمية على أساس مجموعة من الأحداث المتفاعلة ، في كل منها نظام معين من الإجراءات ، مترابطة. يتيح ذلك ببساطة تنفيذ آلية تغيير مساحة الحالة عند اختيار العقدة التالية في فرع حل المشكلة (التتبع الأمامي) ، أو محو آثار الإجراءات التي تم تنفيذها مسبقًا ، عند العودة لخطوة واحدة أو أكثر (تتبع للخلف). لا توجد متطلبات خاصة لحجم الذاكرة أو سرعة المعالج في الخوارزمية.

بناءً على هذه الخوارزمية ، تم العثور على جميع الحلول التسلسلية (قصيرة وكاملة) لقيم مختلفة في مصفوفة الحل n = (7 ، ... ، 16). نظرًا لأن حجم قائمة الحلول الكاملة هو التسلسل المسمى The Encyclopedya On-Line Encyclopedya of Integer Sequences (sequence A000170 [9]) ويشار إليه في العديد من المنشورات ، يبدو من المثير للاهتمام بالنسبة لي أن أسرد حجم قائمة جميع الحلول (short + full) لقيم n التي نظرنا فيها: 7 (194) ، 8 (736) ، 9 (2 936) ، 10 (12 774) ، 11 (61 076) ، 12 (314 730) ، 13 (1 716 652) ، 14 (10 030 692) ، 15 ( 62 518 772) ، 16 (415 515 376).

علاوة على ذلك ، باستخدام الحلول الموجودة ، نعطي صياغة بعض المشاكل وطرق حلها ووصف النتائج.

1. مساحة الدولة التي يتم فيها البحث عن الحلول

يؤدي تعداد الخيارات المختلفة لترتيب الملكات في صفوف معينة من مصفوفة من قرار بالحجم n إلى تكوين مساحة الحالة. إذا لم يكن هناك أي حظر على ترتيب الملكات في خلية واحدة أو أخرى من المصفوفة ، فإن حجم مساحة الولاية سيكون n ⁿ . إذا أخذنا في الاعتبار فقط القاعدة التي تحظر موقع أكثر من ملكة في كل صف وكل عمود ، فسنحصل على مجموعة فرعية من مساحة الولاية التي سيكون حجمها n! تتوافق هذه المجموعة الفرعية من مساحة الولاية مع مشكلة توزيع n بواسطة الرخ. إذا أخذنا في الاعتبار ، إلى جانب هذا ، القاعدة التي تحظر موقع أكثر من ملكة على الأقطار اليسرى واليمنى التي تمر عبر الخلية التي توجد بها الملكة ، فسنحصل على بعض مساحة البحث التي سيكون حجمها أقل من n! .. نسميها مجموعة فرعية من مساحة الحالة - مساحة بحث مثمرة ، بناءً على حقيقة أنه في هذه المساحة الفرعية فقط ، كل الحلول الممكنة. أي فروع مكتملة في مساحة البحث الإنتاجية هي حلول مع عدد معين من الملكات الموضوعة بشكل صحيح. في الأساس ، هذه قرارات قصيرة ، والجزء الصغير المتبقي منها فقط قرارات كاملة.

يوضح الشكل 1 الرسوم البيانية للوغاريتم الطبيعي لثلاثة مؤشرات: أ) القيمة الفعلية (ن!) في حجم مصفوفة القرار ؛ ب) عدد جميع القرارات (قصيرة وكاملة) ؛ ج) عدد الحلول الكاملة ، حسب حجم مصفوفة الحل (ن). كما هو متوقع ، تتميز جميع المنحنيات بزيادة هائلة مع زيادة n. تختلف معدلات نمو عدد كل الحلول وعدد الحلول الكاملة ، على الرغم من أن هذا ليس ملحوظًا على الرسم البياني ، نظرًا لصغر حجم عينة القيم n. على سبيل المثال ، بالنسبة إلى n = 13 ، يكون الفرق بين لوغاريتمات هذه المؤشرات هو 3.148 ، وبالنسبة لـ n = 16 ، يزيد هذا الفرق بمقدار 0.190 ويبلغ 3.338. من الواضح ، مع زيادة أخرى في n ، سيكون هذا التناقض أكثر أهمية.

الشكل 1: اعتماد لوغاريتم حجم مساحة الولاية على القيمة n

2. كيف تتغير نسبة القرارات الكاملة في القائمة العامة لجميع القرارات؟

من الواضح ، إذا كان معدل نمو عدد الحلول الكاملة متخلفًا عن معدل نمو عدد الحلول ، فسوف يقل احتمال العثور على حل كامل في القائمة العامة لجميع الحلول مع زيادة قيمة n. يوضح الشكل 2 رسم بياني لنسبة الحلول الكاملة في القائمة العامة لجميع الحلول على قيمة n. يُرى أنه مع زيادة حجم مصفوفة الحلول ، تنخفض حصة جميع الحلول الكاملة في القائمة العامة. بالنسبة للقيم الأولية n = (7 ، ... ، 14) ، تنخفض هذه القيمة 5.66 مرة من القيمة 0.2062 إلى 0.0364 ، ثم يستمر الانخفاض التدريجي غير المقارب في هذه القيمة. هنا ينشأ تناقض رسمي بين بيانين: من ناحية ، يزداد عدد الحلول الكاملة أضعافا مضاعفة مع زيادة n ، ومن ناحية أخرى ، فإن احتمال الحل الكامل في قائمة متسلسلة من جميع الحلول يتناقص باستمرار. يتم شرح هذه التناقض الظاهر بكل بساطة ، حيث يزداد حجم المساحة الإنتاجية والحجم المرتبط بقائمة جميع الحلول بشكل أسرع مع زيادة عدد الحلول الكاملة. هذا مثل محاولة العثور على إبرة في كومة قش - كمية القش "مع زيادة n" تنمو بشكل أسرع من عدد الإبر التي فقدت هناك. لذلك ، يمكننا أن نفترض أنه إذا كانت n = 27 ، فإن عدد الحلول الكاملة هو 2.346 * 10 ^{17 تقريبًا} ، فإن القيمة المقابلة لعدد الحلول جميعها ستكون على الأرجح 3-4 أوامر بحجم أكبر من ~ 10 ²⁰

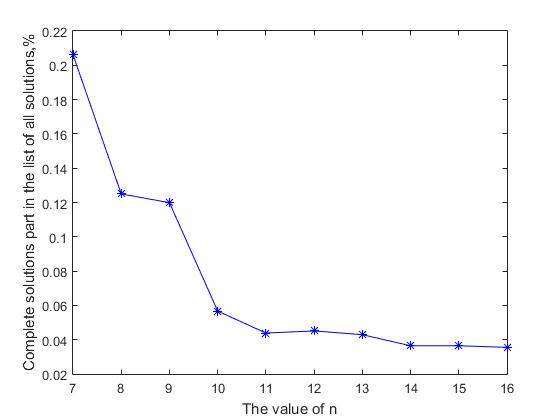
الشكل 2: انخفاض نسبة الحلول الكاملة في القائمة العامة لجميع الحلول مع زيادة n

3. ما هو تكرار الحلول بأطوال مختلفة في قائمة جميع الحلول؟

كما ذكرنا سابقًا ، فإن جميع الفروع المكتملة في مساحة البحث الإنتاجية هي حلول لها عدد مختلف من الملكات الموضوعة بشكل صحيح.
إنها تهمنا بتكرار وجود حلول بأطوال مختلفة في القائمة العامة لجميع الحلول.

يعرض الجدول 1 للقيم n = (7 ، ... ، 12) القيم المقابلة للترددات النسبية للحلول ذات أطوال مختلفة. يظهر التمثيل المرئي المقابل لهذه البيانات في الشكل 3.

يسمح لنا تحليل الجدول باستخلاص الاستنتاجات التالية:

أ) لكل مصفوفة من الحجم n ، يوجد طول معين للحل ذو تردد أقصى (مظلل بالخط العريض).

جدول 1. التردد النسبي (٪) لحلول أطوال مختلفة (k) لمصفوفة بالحجم n = (7 ، ... ، 12)

ن \ ك	4	5	6	7	8	9	10	11	12
7	10.31	31.23	27.84	20.62
8	2.45	20.38	34.78	29.89	12.50
9	0.34	5.79	21.73	35.83	34.32	11.99
10	0.05	1.35	8.41	25.62	32.94	25.96	5.67
11		0.15	2.12	11.80	26.71	34.47	20.36	4.39
12		0.01	0.29	3.28	13.56	29.88	31.29	17.18	4.51

ب) مع زيادة n ، يزداد عدد الحلول بأطوال مختلفة. وفقًا لذلك ، يقل التكرار النسبي لجميع القرارات.

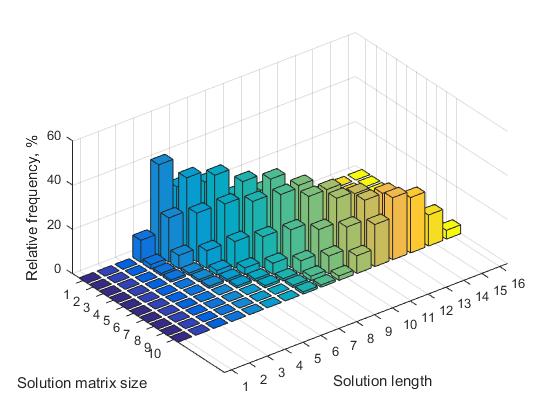
الشكل 3 تواتر الحلول بأطوال مختلفة حسب حجم مصفوفة المحلول ، n = 7 ، ... ، 16

ج) لكل مصفوفة من الحجم n ، يوجد حد أدنى معين لطول الحل ، وفيما يلي حلول قصيرة لا تحدث. مع زيادة n ، تزداد قيمة هذه العتبة. على سبيل المثال ، بالنسبة إلى n = 8 ، قيمة العتبة هي 4 ، على التوالي ، بالنسبة إلى n = 16 ، قيمة العتبة هي 7.

4. ما هو الترتيب النسبي للحلول الكاملة في قائمة متسلسلة لجميع الحلول؟

في بيان المشكلة "حول توزيع الملكات" ، لا توجد أسباب من شأنها أن تعطي أي سبب لإبداء أي افتراض حول تسلسل القرارات الكاملة في القائمة العامة لجميع الحلول. كنا مهتمين بما إذا كانت الحلول الكاملة في القائمة العامة موزعة بالتساوي أو بشكل عشوائي أو إذا كانت تحتوي على بعض الخصائص. لمعرفة ذلك ، قمنا بتحليل المسافات بين أقرب الحلول الكاملة في قائمة متسلسلة تضم جميع الحلول. كما يتضح من الشكل 4 ، حيث بالنسبة إلى n = 12 ، يتم تقديم رسم بياني للتغييرات في الترددات المقابلة ،

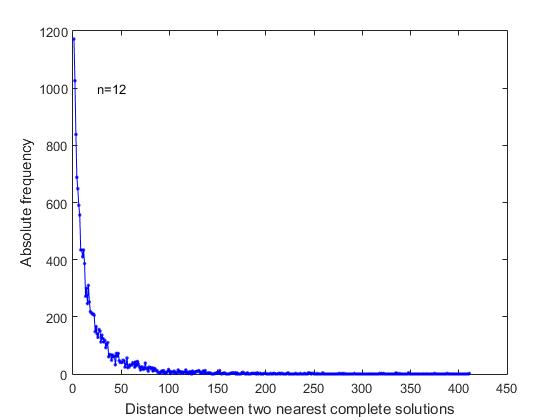
الشكل 4 التردد مقابل المسافة بين أقرب الحلول الكاملة في قائمة متسلسلة لجميع الحلول الكاملة (ن = 12)

مع أكبر تردد ، توجد حلول كاملة تتبع بعضها البعض على الفور في قائمة متسلسلة مشتركة لجميع الحلول. هذه هي حالات تكوين فرع البحث عندما تسمح لك علاقة المواضع المجانية في الأسطر الأخيرة بتكوين حلين متكاملين أو أكثر. علاوة على ذلك ، الحد الأقصى للتردد هو تلك الحلول الكاملة التي تقع بين: حل قصير واحد ، حلان قصيران ، إلخ.

5. هل هناك نمط في ترتيب الحلول الكاملة في القائمة العامة لجميع الحلول؟

للإجابة على هذا السؤال ، قمنا بتحليل قوائم متسلسلة لجميع الحلول للقيم n = (7 ، ... ، 16). لإظهار النتائج بوضوح ، في الشكل 5 ، بالنسبة للقيمة n = 8 ، يتم تقديم رسم بياني حيث يتم الإشارة إلى طول كل حل في قائمة الحلول السبعة 736 على التوالي. هنا ، هناك 92 حلًا مكتملًا فقط وتم إبرازها باللون الأحمر ، بينما تبقى الحلول 644 المتبقية قصيرة ومظللة باللون الأزرق. يمكن ملاحظة أن الحلول الكاملة ليست موزعة بالتساوي في قائمة جميع الحلول. هناك مجالات تكون فيها الحلول الكاملة أكثر شيوعًا ، وهناك أماكن تكون فيها الحلول الكاملة نادرة أو لا تكون على الإطلاق.

الشكل 5: طول كل حل في قائمة متتابعة لجميع الحلول ، لمصفوفة 8 × 8 (حلول كاملة الأحمر ، حلول قصيرة - زرقاء). العدد الإجمالي لجميع الحلول هو 736

ومع ذلك ، هناك شيء آخر مهم هنا. إذا نظرت بعناية إلى الشكل الذي يشبه الباركود الأزرق والأحمر ، ستلاحظ ميزة واحدة مهمة للغاية ، فكل الخطوط الحمراء متناظرة فيما يتعلق ببعض الخطوط الرأسية الشرطية التي تمر عبر قائمة الحلول. في الواقع ، كما هو موضح في الاختيار ، إذا كان هناك حل كامل في الخطوة رقم i من بداية القائمة العامة ، وبناءً عليه ، سيتم العثور على حل كامل بالتأكيد في الخطوة m-i + 1. على سبيل المثال ، بالنسبة إلى n = 8 ، إذا ظهر الحل الكامل الأول في البحث المتسلسل لجميع الحلول في الخطوة 43 ، فتبعًا لذلك ، سيتم العثور على الحل الكامل الأخير في القائمة في الخطوة 736–43 + 1 = 694. إذا ظهر الحل السابع عشر لمصفوفة 10x10 في القائمة في الخطوة 368 ، فسيظهر الحل الكامل المتماثل لها في قائمة جميع الحلول في الخطوة 12774-17 + 1 = 12407. تسري هذه القاعدة على مصفوفة القرار من أي حجم. لذلك ، يمكننا صياغة قاعدة. بالنسبة لأي قيمة n ، إذا كان في القائمة التسلسلية لجميع الحلول ، في الموضع رقم i من بداية القائمة ، يكون الحل كاملاً ، ثم يكون الحل المتماثل من نهاية القائمة الموجودة في الموضع m-i + 1 كاملاً (قاعدة تناظر الحلول). m, , . , n, , . ( – ).

, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).

, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,

<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b> 

تعني هذه القاعدة أنه في حالة الحصول على حل كامل في الخطوة الأولى ، يصبح الحل الكامل المتماثل في الخطوة m - i +1 معروفًا . لذلك ، عند البحث عن جميع الحلول الكاملة ، يكفي العثور على النصف الأول فقط من الحلول الكاملة. يمكن تحديد النصف الثاني من قائمة الحلول الكاملة من الحلول التي تم الحصول عليها بالفعل ، بناءً على قاعدة التكامل. المعيار المتمثل في تحقيق نصف قائمة الحلول الكاملة هو تحقيق قاعدة التكامل بين الحل الكامل السابق Q (i-1) و Q (i) اللاحقة. بمعنى أنه من الضروري أن يكون مجموع كل زوج من المؤشرات المقابلة لحلين متتالين يساوي n + 1 . نظرًا لأن أي حل كامل من قائمة جميع الحلول الكاملة فريد من نوعه ، فلن تكون الحلول الكاملة المتتالية سوى تلك الحلول التكميلية الموجودة على جانبي الحدود التي تقسم القائمة إلى نصفين.

ستسمح هاتان القاعدتان في المستقبل ، عند البحث عن جميع الحلول الكاملة لأي قيمة تالية لـ n ، بتقليل مقدار الحساب ، وبالتالي تقليل وقت الحساب إلى النصف.

6. تصور تسلسل الخطوات لإيجاد الحل الكامل الأول

كيف يتم تنفيذ الخطوات إلى الأمام (تتبع للأمام) والعودة (تتبع للخلف) عند تشكيل فرع من البحث عن حل؟ للإجابة على هذا السؤال ، قررنا ، بالنسبة لمصفوفة 10 × 10 ، تسلسل التحولات 194 الأولية بين السطور حتى يظهر الحل الكامل الأول. يظهر الرسم البياني المقابل في الشكل 6. الخطوط الزرقاء تشير إلى حركة إلى الأمام ، والخطوط الحمراء تشير إلى عودة. خلال هذه الخطوات 194 ، تم إنشاء 35 حلول قصيرة. يوضح الشكل أن معظم التحولات (84.5٪) تحدث بين السطور (5 ، 6 ، 7 ، 8). هذا نوع من "عنق الزجاجة" في الطريق إلى "الهدف". على النحو التالي من الشكل ، لا يوجد سوى 7 حالات للتبديل إلى السطر الرابع وحالة واحدة للتبديل إلى السطر الثالث. هناك أيضًا 13 حالة للتبديل إلى السطر التاسع. لم تنجح ثلاث محاولات للانتقال إلى السطر العاشر ، لأنه في فروع البحث هذه الموجودة في السطر العاشر لم يكن هناك موضع فارغ. هذا المثال يوضح جميع فروع قصيرة

الشكل 6: تصوُّر أحداث التراجع (الأحمر) والتقديم (الأزرق) لخطوات البحث الأولى البالغ عددها 194 (ن = 10)

الحلول ، حتى الحل الكامل الأول. ستكون أي خوارزمية لحل هذه المشكلة فعالة إذا كانت تحتوي على آلية من شأنها القضاء على جميع (أو جزء) الفروع التي تؤدي إلى حلول قصيرة.

7. بعد كم من القرارات القصيرة يظهر الحل الكامل الأول؟

بالنظر إلى أن الحلول الكاملة تظهر بشكل مختلف على أجزاء مختلفة من قائمة جميع الحلول ، يبدو من المهم معرفة عدد الحلول القصيرة التي يظهر فيها الحل الكامل الأول عند البحث في جميع الحلول بطريقة متسلسلة. لهذا الغرض ، بالنسبة للقيم n = (7 ، ... ، 35) ، تم حساب جميع الحلول القصيرة على التوالي حتى ظهور أول حل كامل. كما يتضح من الشكل 7 ، الذي يظهر رسم بياني للاعتماد على n ، اللوغاريتم الطبيعي لرقم الخطوة ، عند ظهور الحل الكامل الأول ، حتى بالنسبة لقيم n ، يظهر الحل الكامل الأول متأخراً أكثر بكثير من أقرب القيم الفردية لـ n. على سبيل المثال ، بالنسبة للقيمة الفردية n = 21 ، يظهر الحل الكامل الأول في الخطوة 3138 ، وبالنسبة للقيمة الزوجية التالية n = 22 ، يظهر الحل الكامل الأول في الخطوة 628169. وفقًا لذلك ، بالنسبة للقيمة الفردية التالية n = 23 ، يظهر الحل الكامل الأول في الخطوة 9155.

الشكل 7: عدد الحلول القصيرة حتى الحل الكامل الأول ، لقيم مختلفة من n

عدد خطوات التكرار حتى n = 22 هي 200.2 و 68.6 مرة ، على التوالي ، من أقرب القيم الفردية. هذا واضح بشكل خاص في حساب وقت n = 34. هنا ، يظهر الحل الكامل الأول في الخطوات 818 337 184 ، وللحصول على أقرب الأرقام الفردية (33 ، 35) ، على التوالي ، في 50 704 900 و 84 888 759 الخطوات. يجب أن يقال أيضًا عن انتهاك النمو الرتيب لعدد الحلول القصيرة قبل ظهور الحل الكامل الأول ، مع زيادة n. بالنسبة لقيم n ، يحدث هذا في n = 19 ، بالنسبة للقيم الفردية ، في n = 24 و n = 26.

8. هل تردد الخلية لكل صف في قائمة جميع الحلول الكاملة هو نفسه؟

تشبه مصفوفة القرار بحجم nxn ، والتي تُعد بمثابة تناظرية لشطرنج ، مشهدًا تحدث فيه جميع الأحداث. أي حل كامل يتكون على هذا المشهد يتكون من مؤشرات خلايا من صفوف مختلفة ، لأن كل خلية من هذه الخلايا هي عقدة في فرع البحث عن الحلول. والسؤال الذي يهمنا هو التالي: هل الحمل في كل صف هو نفسه بالنسبة للخلايا المختلفة عند تشكيل قائمة بجميع الحلول الكاملة؟ من الواضح أنه كلما زادت قيمة التردد ، زاد نشاط هذه الخلية في تشكيل قائمة من الحلول الكاملة. لتحديد ذلك ، نحدد لكل صف ، بناءً على قائمة بجميع الحلول الكاملة ، التردد النسبي لمختلف المؤشرات. أولاً ، نقوم بتحليل مصفوفة الحلول بحجم ن = 8. دعونا نفحص كل صف من صفيف الحلول الكاملة بالتتابع وتحديد تواتر قيم الفهرس المختلفة. يوضح الجدول 2 القيم المقابلة لترددات النشاط المطلق للخلايا المختلفة في كل من الصفوف الثمانية ، وفي الشكل. 8

الجدول 2. التكرار المطلق لنشاط الخلية في كل من الصفوف الثمانية لمصفوفة القرار 8 × 8 ، استنادًا إلى تحليل قائمة بجميع الحلول الكاملة

الصف \ العقيد	1	2	3	4	5	6	7	8
1	4	8	16	18	18	16	8	4
2	8	16	14	8	8	14	16	8
3	16	14	4	12	12	4	14	16
4	18	8	12	8	8	12	8	18
5	18	8	12	8	8	12	8	18
6	16	14	4	12	12	4	14	16
7	8	16	14	8	8	14	16	8
8	4	8	16	18	18	16	8	4

يتم تقديم مجموعة من 4 رسوم بيانية ، حيث يميز كل رسم بياني التغير في الترددات النسبية داخل سطر واحد. أحد الاستنتاجات المهمة بشكل أساسي التي يمكن استخلاصها من تحليل جميع البيانات التي تم الحصول عليها هي كما يلي:

• بالنسبة لمصفوفة القرار ذات الحجم التعسفي n ، يتزامن نشاط خلايا الصف الأول مع نشاط الخلية n-i + 1 ، أي يتزامن نشاط خلايا الصف الأول دائمًا مع نشاط خلايا الصف الأخير ، على التوالي ، يتزامن نشاط خلايا الصف الثاني مع نشاط خلايا الصف ما قبل الأخير ، إلخ.
  
  إذا كان n غريبًا ، فلن يكون للصف الأوسط لمصفوفة الحل سوى زوج متماثل ؛ بالنسبة لجميع الخلايا الأخرى ، تكون القاعدة أعلاه صالحة
• نحن نسمي هذا "خاصية التماثل الأفقي لنشاط خلايا الصفوف المختلفة لمصفوفة الحل" . لهذا السبب ، قدمنا ​​فقط 4 رسوم بيانية لمصفوفة القرار بالحجم n = 8 ، حيث أن الرسوم البيانية المقابلة لنشاط الخلية للصفوف (1 ، 8) ، (2.7) ، (3.6) و (4.5) متطابقة تمامًا.

تجدر الإشارة أيضًا إلى أن قيم التردد متماثلة حول المحور العمودي الذي يقسم المصفوفة إلى جزأين متساويين (في حالة القيمة الزوجية n) ، أو تمر عبر العمود المتوسط ​​(في حالة القيمة الفردية n). نحن نسمي هذا "خاصية التناظر العمودي لنشاط خلايا الصفوف المختلفة لمصفوفة الحل" .

بالإضافة إلى ذلك ، على النحو التالي من تحليل الجدول 2 ، تكون الترددات في مصفوفة الحلول متماثلة فيما يتعلق بالأقطار الرئيسية اليمنى واليسرى.

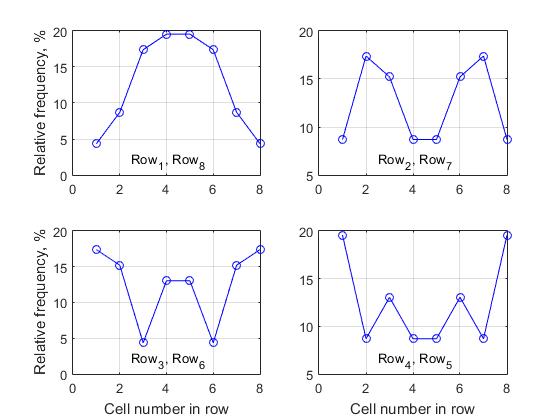
الشكل 8: نشاط الخلية للصفوف المقابلة عند تشكيل قائمة الحلول الكاملة ، n = 8

أعتقد أن وجود قواعد تقييدية في بيان المشكلة ، والملكية ذات الصلة بعدم الحتمية ، "تشكل" نوعًا من العلاقة المتناغمة بين العقد في خطوط مختلفة. تلك الفروع من البحث التي تتوافق مع هذه القواعد - تؤدي إلى تشكيل حل كامل. تنتهك الفروع المتبقية من البحث ، في مرحلة ما ، هذه القواعد ، ونتيجة لذلك ، "أكمل رحلتهم" في شكل قرارات قصيرة. تجدر الإشارة هنا إلى أن خلايا مصفوفة القرار لها علاقة محلية فقط ضمن مجموعة تأثير الإسقاط ، ولا توجد قواعد محددة للإجراءات المنسقة بينها. النشاط الجماعي للخلايا هو فقط نتيجة لتأثير القواعد التقييدية. لذلك ، يبقى السؤال المثير للاهتمام مفتوحًا ، كيف تؤثر القواعد التقييدية ، مثل العوامل غير الحتمية ، على خلايا مصفوفة القرار ، والتي تؤدي في النهاية إلى تكوين مصفوفة نشاط خلية "متناغم" - متناظرة فيما يتعلق بالمحاور الأفقية والعمودية ، وكذلك فيما يتعلق باليسار والأقطار الرئيسية اليمنى. هل هذه خاصية مميزة لهذه المشكلة فقط ، أم أنها تنطوي أيضًا على مشكلات غير حتمية أخرى؟

9. من أي رقم سطر يتم تشغيل خوارزمية التتبع إلى الأمام؟

إذا تابعنا تشغيل خوارزمية اختيار الصف المتسلسل في مصفوفة القرار الخاصة بمكان الملكة ، يمكننا أن نرى أنه بدءًا من سطر معين ، والذي سنطلق عليه "StopRow" ، فإن عملية المضي قدمًا "braked". في فرع البحث ، هذا هو السطر الأول الذي توجد فيه مشاكل في التوفر المجاني

شكل 9-1 اعتماد نسبة مؤشر StopRow إلى n على حجم مصفوفة القرار (الجزء الأول)

موقف لموقع الملكة. من هذا الخط يتم تشغيل خوارزمية تتبع الرجوع لمسح آثار الإجراءات التي تم تنفيذها سابقًا والعودة مرة أخرى. هذا هو الخط الذي يظهر فيه الحل القصير الأول.

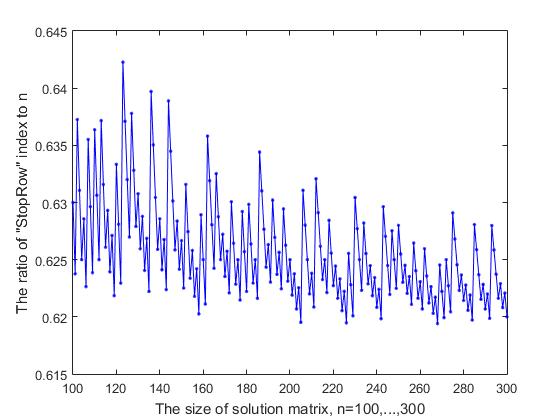
الشكل 9-2 اعتماد نسبة مؤشر StopRow إلى n على حجم مصفوفة القرار (الجزء 2)

يعتمد مؤشر خط "StopRow" ، الذي تبدأ به الصعوبات في المضي قدمًا ، على الحجم n لمصفوفة القرار. إذا أخذنا في الاعتبار نسبة هذا المؤشر ، التي نشير إليها بواسطة StopInd إلى حجم مصفوفة الحل n ، عندئذ ، كما يتضح من الشكل 9-1 ، حيث يتم عرض نتائج الحساب للقيم الأولية n = (7 ، ... ، 99) ، تتقلب هذه النسبة إلى حد أكبر أو أقل الجانب ويميل إلى الانخفاض. مع زيادة في n = (100 ، ... ، 300) ، تتقلب هذه النسبة بين 0.619 - 0.642 (الشكل 9-2) ، ومع زيادة أخرى في n ، نحصل على النتائج التالية (يتم إعطاء قيم n بالتسلسل ، وتكون القيمة بين قوسين نسبة StopInd و StopInd / n: 1000 (619 ، 0.6190) ، 2000 (1239 ، 0.6195) ، 3000 (1856 ، 0.6187) ، 4000 (2473 ، 0.6182) ، 5000 (3091 ، 0.6182). -line يقسم مصفوفة القرار وفقًا لقاعدة النسبة الذهبية : أي أن نسبة StopInd / n تختلف عن (n-StopInd) / StopInd بمقدار صغير يميل إلى الصفر مع زيادة n. على سبيل المثال ، بالنسبة إلى n = 5000 ، الفرق بين العلاقات 3091/5000 و 1909/3091 هو 0.006 ، وهو أقل من 0.1 ٪ من متوسط ​​هاتين العلاقتين.

الرسم البياني هو مبين في الشكلين 9- (1،2) لديه شكل غير عشوائي من التباين ، والذي يشبه تسجيل على "العصا الموسيقية". القفزات المتكررة للأعلى والسقوط المتدرج مرئية مع بعض الدورية غير المنتظمة. من الواضح أن هناك سببًا لهذا النوع من سلوك المنحنى ، وربما يكون هذا الأمر ذا أهمية للبحث. لهذا السبب ، لغرض التصور الأكثر تفصيلا ، تم تقديم الرسم البياني في شكلين.

لقد فكرت فقط في جزء من الأسئلة التي يمكن صياغتها على أساس نتائج حل مشكلة "توزيع الملكات". آمل أن تجعل النتائج التي تم الحصول عليها آليات تشكيل العمليات غير الحتمية والتغييرات في مساحة الدولة أكثر شفافية من أجل الفهم. ربما سيكون هذا بمثابة نقطة ارتكاز لصياغة مهام جديدة والمضي قدما.

الخاتمة

• إذا نظرنا إلى المنشور ، توصلنا إلى استنتاج ، فمن الطبيعي أن يطرح السؤال التالي: "ماذا يعني حل مشكلة المليار ملكة في عنوان المقالة؟" في إعداد المنشور الخاص بـ "هبر" ، اعتقدت أن الشخص الذي لديه ، على سبيل المثال ، منجم يتم فيه استخراج الماس ، يجب أن يعطي كل واحد على الأقل لأصدقائه وأقاربه ، وإلا فإنه سيكون غير عادل. لذلك ، أود أن أقدم هدية لجميع أعضاء مجتمع habr: المشاركون ، المنظمون ، الزوار. كما يوحي الاسم ، هذا هو الحل لمشكلة توزيع مليار ملكة على رقعة الشطرنج مليار حجمها.
  
  بالطبع ، هذا ليس ماسًا ذو أوجه ، لكن بالنسبة لخبراء الفن الفكري الحقيقيين ، يمكن أن يكون أكثر قيمة من "نوع من الماس هناك". علاوة على ذلك ، يختلف الماس في جميع أنحاء العالم ، وهذا الحل موجود في نسخة واحدة فقط حتى الآن. ولدينا بايت الله (*) يرى أنني أفعل هذا بإخلاص.
  الحل الناتج هو مجموعة أحادية البعد من مليار رقم ، والتي يتم تقديمها بتنسيق MatLab .mat ومتاح على: One Billion Queens Problem Solution على Google Drive
  -العنصر الأول من هذه المجموعة يميز موقف الملكة في السطر الأول ، العنصر الثاني - الموضع في السطر الثاني ، إلخ. هذا هو مجرد حل واحد من بين nBillion الحلول الممكنة. وقيمة nBillion هي عدد كبير بحيث يمكن اعتباره قريبًا من اللانهاية.
  
• يبدو لي أن هذا الحل يمكن أن يعزى إلى فئة القيم الفكرية الافتراضية. يمكننا القول أن "هذا شيء يوجد فيه شيء ما". لا يمكن "لمسها" ، لذلك لا يتم إدراكها في الوعي إلا على مستوى الأحاسيس. هناك ، في الواقع ، هناك ترتيب مذهل ووئام واضح وصريح. هذه هدية رمزية بحتة (حرفيًا ومجازيًا) موجهة إلى جميع أفراد المجتمع. أعتقد ، " أنت لست مثل أي شخص آخر ."
  
  (آمل أن يقوم شخص ما "بأخذ الهدية إلى المنزل." حجم الملف كبير بما يكفي - 3.7 جيجابايت. هذه بيانات نظيفة ومعتمدة. سيعرض Google Drive تحذيرات - تعامل مع هذا بفهم)
  
• قبل اتخاذ هذا القرار ، فكرت في الطبيعة الجماعية الفردية لمثل هذه الهدية. هل من الممكن تقديم نسخة أصلية واحدة والباقي بنسخ؟ لكن الحل بسيط. المفاهيم "اليومية" المعتادة لكل من "الأصلي" و "نسخة" ، في هذه الحالة ، تفقد معناها. نحن لا ننسخ ، ولكن إنشاء نسخة أصلية أخرى. و "النسخ الأصلية" هي نفسها للجميع ومتساوية.
  
• أعتقد أنه في شركة الأقارب ، من المرجح أن تكون الشخص الوحيد الذي حصل على مثل هذا "المنتج الفكري" كهدية. سيكون من الممتع أن تخبر حماتك عن هذه الهدية: "تخيل أمًا بلوحة رقعة بطول 50000 كم بواقع 50،000 كيلومتر ، والتي يتم توزيع مليار ملكة عليها بطريقة لا يرى بها الآخر الآخر من مسافة قريبة ...". من يدري ، ربما بعد هذا ، سيكون صهر زوجته موضع تقدير أكبر ، لأنه يقدم له هدية غريبة.
  

أتمنى لجميع أفراد المجتمع الصحي habr ، النجاح والرفاه. أتمنى أن يأتي العام الجديد بالتوفيق للجميع.

(*) - نظرًا لأنه يشير إلى اسم الكائن ، فيجب أيضًا تقديم الوصف الخاص به.
البايت الله يعني كيانًا متعدد الأبعاد ، يتكون من أصفار وكائنات ، معقول بكل معنى الكلمة وغير محدود في جميع الاتجاهات. أي تسلسل من الأصفار وتلك الموجودة في هذا الفضاء يمثل معرفة معينة.

المراجع

[4] ماكس بيزل ، اقتراح مشكلة 8 ملكات "، برلينر شاشيتونج ، المجلد
3 (1848) ، صفحة 363. (مقدم تحت اسم المؤلف \ Schachfreund ".)

[5] فرانز نوك ، Briefwechseln mit allen fur alle "، Illustrirte Zeitung ، المجلد
377 رقم 15 (1850) ، صفحة 182.

[6] بيل جوردان ؛ ستيفنز بريت (2009). "دراسة استقصائية للنتائج المعروفة ومجالات البحث للملكات ن." الرياضيات المنفصلة. 309 (1): 1-31

[7] جنت ، إيان ب. جيفرسون ، كريستوفر ؛ العندليب ، بيتر (أغسطس 2017). "تعقيد إنجاز كوينز". مجلة بحوث الذكاء الاصطناعي. مطبعة AAAI. 59: 815-488

[8] W. Kosters and all، n-Queens - 342 reference، (November 20، 2018)

[9] NJA Sloane ، الموسوعة على الإنترنت لتسلسل صحيح ، نشرت إلكترونياً. 2016