النماذج الرياضية للفوضى

مقدمة

ناقش هابر بالفعل نظرية الفوضى في المقالات [1،2،3]. يتم النظر في الجوانب التالية لنظرية الفوضى في هذه المقالات: مخطط عام لمولد تشوا ؛ نمذجة ديناميات نظام لورنتز ؛ جاذبات مبرمجة من قبل الدوائر المتكاملة المنطق لورنتز ، ريسلر ، Rikitake و Nose-Hoover.

ومع ذلك ، تُستخدم تقنيات نظرية الفوضى أيضًا لنمذجة النظم البيولوجية ، والتي ، بلا شك ، واحدة من أكثر النظم الفوضوية على الإطلاق التي يمكن تخيلها. واستخدمت أنظمة المعادلة الديناميكية لنمذجة كل شيء من السكان والنمو الوبائي إلى دقات القلب الإيقاعية [4]

في الواقع ، يمكن تصميم أي نظام فوضوي تقريبًا - سوق الأوراق المالية يولد منحنيات يمكن تحليلها بسهولة باستخدام جاذبات غريبة ، عملية إسقاط القطرات من حنفية مانعة للتسرب تكون عشوائية عند تحليلها بالأذن المجردة ، ولكن إذا تم تصويرها على أنها جاذبة غريبة ، فإنها تفتح ترتيب خارق لا يمكن توقعه من الوسائل التقليدية.

الغرض من هذه المقالة هو دراسة نظرية الفوضى باستخدام مثال زيادة عدد المجموعات البيولوجية ومضاعفة دورة النظم الميكانيكية مع التصور الرسومي للنماذج الرياضية القائمة على برامج بديهية بسيطة مكتوبة في بيثون.

كُتب المقال بغرض التدريس ، ولكنه سيسمح للقارئ الذي لا يتمتع بخبرة في البرمجة باستخدام البرامج المذكورة أعلاه لحل معظم المشكلات التعليمية الجديدة بشكل مستقل عن موضوع نمذجة ظواهر الفوضى.

مضاعفة فترة الدورات والفوضى على مثال نمو عدد المجموعات البيولوجية

لنبدأ بالنظر إلى المعادلة التفاضلية اللوجستية التي تمثل زيادة محدودة بدلاً من الأسية في عدد المجموعات البيولوجية:

$$$\ frac {dN} {dt} = aN-bN ^ {2} ، (a ، b> 0). (1) دولا$

هذه المعادلة هي التي يمكنها التنبؤ بأنماط سلوك غريبة وغير متوقعة لبعض السكان. في الواقع ، وفقا ل (1) ، ل $$$t \ rightarrow + \ infty$ يقترب حجم السكان من الحدود التي تساوي a / b .

بالنسبة للحل الرقمي للحل التفاضلي اللوجستي ، يمكنك استخدام أبسط الخوارزميات ، مع القيمة العددية للخطوة الزمنية ، مع الأخذ في الاعتبار $$$t_ {n + 1} = t_ {n} + h$ ، ثم يمكن الحصول على الحل (1) بتطبيق العلاقة التالية بشكل متكرر:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$ (2)

نحن نمثل المعادلة (2) في شكل معادلة لوجستية في فروق محدودة:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ . (3)

حيث: r = 1 + آه و s = bh .
تبديل في (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$ نحصل على الصيغة التكرارية:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ ، (4)

حساب القيم المعطاة بالعلاقة (3) ، يمكننا توليد تسلسل $$$x_ {1} ، x_ {2} ، x_ {3} ، .....$
الحد الأقصى لقيم عدد السكان التي ستدعمها البيئة في أوقات معينة $$$t_ {1} ، t_ {2} ، t_ {3}.$ .

نحن نفترض أن هناك قيمة محددة للكسور التي تعبر عن جزء من حجم السكان:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ ، (5).

سنبحث كيف يعتمد $$$x _ {\ infty}$ من معامل النمو r في المعادلة (4). للقيام بذلك ، في بيثون ، نكتب برنامجًا يبدأ من $$$x_ {1} = 0.5 دولا$ يحسب النتائج في عدة مئات من التكرارات ( ن = 200 ) لـ r = 1.5 ؛ 2.0 ؛ 2.5 :


نتيجة البرنامج (لتقليل ناتج النتائج ، يتم إعطاء القيم الثلاثة الأولى والأربعة الأخيرة):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

يوضح تحليل النموذج المنفصل أنه بالنسبة إلى r = 1.5 ؛ 2.0 ؛ 2.5 مع زيادة عدد التكرارات ، فإن القيمة $$$x_ {n}$ يستقر ويصبح مساويا تقريبا للحد $$$x _ {\ infty}$ والذي يحدد بالعلاقة (5). علاوة على ذلك ، بالنسبة للقيم المحددة لـ r ، الكمية $$$x _ {\ infty}$ متساوية في المقابل $$$x _ {\ infty} = 0.3333 ؛ 0.5000 ؛ 0.6000 دولا$ .
نحن نزيد r = 3.1؛ 3.25؛ 3.5 وعدد التكرارات n = 1008 ، لهذا نقوم بإجراء التغييرات التالية على البرنامج:


نتيجة البرنامج (لتقليل ناتج النتائج ، يتم إعطاء القيم الأربعة الأولى والثماني الأخيرة):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

على النحو التالي من البيانات المذكورة أعلاه ، بدلاً من الاستقرار بالقرب من مجموعة محددة ، يتقلب الجزء الكسري من السكان بين كسرين مع تغير الوقت. مقارنة بـ r = 3.1 ، تتضاعف فترة دورة r = 3.25 ، و r = 3.5 أربع مرات.


نتيجة البرنامج:



بسبب مضاعفة فترة التكرار ، $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ أصبح معروفا على نطاق واسع. عندما تتجاوز قيمة معدل النمو r = 3.56 ، فإن مضاعفة الفترة تتسارع وتنشأ الفوضى القصوى بالفعل عند النقطة r = 3.57 . لعرض بداية الفوضى ، نستخدم البرنامج التالي:


نتيجة البرنامج:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

سنقوم بكتابة برنامج لتصور اعتماد سلوك التكرار على معامل النمو r . لكل قيمة ص في الفاصل $$$a \ leqslant r \ leqslant b$ يتم إجراء 1000 التكرار لتحقيق الاستقرار. ثم ، يتم رسم كل 250 قيمة تم الحصول عليها نتيجة التكرارات على طول المحور العمودي ، وتشكيل نقاط ( ص ، س ):


النتيجة في شكل رسم بياني:



يسمى الرسم البياني الناتج "مخطط فرعي" ، والذي يسمح لك بتحديد ما إذا كانت قيمة r معينة تتوافق مع دورة أم فوضى. يتم تحديد القيمة الوحيدة لحجم السكان على القيمة $$$r \ حوالي 3 دولارا$ ثم دورة مع فترة من 2 إلى $$$r \ تقريبا 3.4 دولا$ ، ثم دورة بفترة 4 ، ثم دورة بفترة 8 فصاعداً مع مقاربة سريعة للفوضى.

تجدر الإشارة إلى أن المناطق الرأسية للمساحة الخالية على الرسم البياني هي المناطق r = 3.6 و r = 3.7 ، بين r = 3.7 و r = 3.8 ، بين r = 3.8 و r = 3.9 حيث يعود الترتيب الدوري من الفوضى السابقة.
للنظر في ظهور دورة مع فترة متعددة من 3 في $$ قم بإجراء تغييرات على البرنامج السابق:


نتيجة البرنامج:



تظهر دورة الفترة 3 في جوار النقطة r = 3.83 ، ثم تنقسم بالتتابع إلى دورات 6،12،24. وجود دورة ذات فترة 3 يعني وجود دورات في أي فترة زمنية محددة ، وكذلك دورات فوضوية دون أي فترة على الإطلاق.

يتيح لك الرسم التوضيحي للفرع متابعة تطوير النظام مع تغيير سلس في المعلمة. باستخدام قيمة ثابتة للمعلمة ، يسمح مخطط العنكبوت (مخطط لاميرا) بتتبع مدارات النقاط.

يتيح لك إنشاء مخطط العنكبوت التعرف على التأثيرات المختلفة غير المرئية على المخطط الفرعي. دعنا نكتب البرنامج:


مخطط لاميرا:

فترة مضاعفة في النظم الميكانيكية

فكر في معادلة تفاضلية تقوم بنمذجة الاهتزازات الحرة المثبطة لنقطة ما من كتلة معيّنة في نبع غير خطي ، حيث يتم تحديد التخميد بالسرعة.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

في المعادلة (6) ، يمثل المصطلح kx قوة الربيع الخطي المطبق على نقطة ما من كتلة معينة ، والمصطلح $$$\ beta x ^ {3}$ يمثل اللاخطية الفعلية في الربيع.

إذا كانت القوة تعمل على نظام التذبذبات الحرة (6) ، فإن وصف النقطة المادية للكتلة التي تطبق عليها هذه القوة يتم وصفه بواسطة معادلة التفريغ التفاضلي للتذبذبات القسرية:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

يتم حل المعادلة (7) لمعظم المعلمات المدرجة فيه عدديا. يظهر الشكل الميكانيكي للنموذج الرياضي وفقًا للمعادلة (7):



من ميزات النظام المعطى أنه بدلاً من الزنبرك ، يتم استخدام خيط معدني مرن ، والذي يتذبذب في مستوى عمودي ، حيث يكون ثابت الخطاف k سالبًا. في هذا المخطط ، نقاط التوازن المستقر (أ) و (ج) ، ونقطة التوازن غير المستقر (ب).

عندما يتم إزاحة نقطة مادية من الموضع (ب) ، تكون القوة المؤثرة عليها مثيرة للاشمئزاز. إذا كانت القوة الدورية ، على سبيل المثال ، التي تم إنشاؤها بواسطة المجال المغنطيسي المتأرجح مبطنة جزئيًا بسبب مقاومة الهواء. ثم ، المعادلة (7) هي نموذج رياضي مقبول للإزاحة الأفقية x (t) لنقطة ما مع نطاقات المعلمة التالية $$$k <0، c> 0، \ beta> 0$ .

لدراسة سلوك مثل هذا النظام غير الخطي ، نأخذ $$$k = -1 ، m = c = \ beta = \ omega = 1$ ثم تأخذ المعادلة التفاضلية (7) الشكل:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ ، (8)

نكتب برنامجًا للتكامل العددي للمعادلة (8) في ظل الظروف الأولية $$$x (0) = 1 ، x ^ {'} (0) = 0$ في المجال $$ ولكل من قيم السعة التالية $$$F_ {0} = 0.6 ؛ 0.7 ؛ 0.75 ؛ 0.8 دولا$ وفي كل حالة ، ارسم الحلول للطائرات $$$x (t) ، x ^ {'} (t)$ و $$$t ، x (t)$ :


الرسوم البيانية نتيجة لهذا البرنامج





يوضح هذا الانتقال من الفترة المضاعفة إلى الفوضى السلوك العام للنظام الميكانيكي غير الخطي استجابةً لتغيير في المعلمة المادية المقابلة ، على سبيل المثال: $$$k ، m ، c ، \ beta ، \ omega ، F_ {0}$ . هذه الظواهر لا تحدث في النظم الميكانيكية الخطية.

جاذبية لورنز

الاستبدال في معادلة Duffing للتذبذبات القسرية (7) يؤدي إلى نظام غير خطي ثنائي الأبعاد للمعادلات التفاضلية ، والذي تم عرضه في القائمة السابقة. نظرت E.N في نظام غير خطي ثلاثي الأبعاد للمعادلات التفاضلية كما هو مطبق على مشاكل الأرصاد الجوية. لورينز:

$$$\ frac {dx} {dt} = - sx + sy ،$
$$$\ frac {dy} {dt} = - xz + rx-y ،$ (9)
$$$\ frac {dz} {dt} = xy-dz$

من الأفضل مشاهدة حل النظام (9) في الإسقاط على إحدى الطائرات الثلاث. سنكتب برنامج تكامل رقمي للمعلمات b = \ frac {8} {3}، s = 10، r = 28 والظروف الأولية x (0) = - 8، y (0) = 8، z (0) = 27 :


نتيجة البرنامج:



بالنظر إلى الصورة على الرسم البياني بمرور الوقت ، يمكن افتراض أن النقطة P (x (t) ، y (t) ، z (t)) تصنع عددًا عشوائيًا من التذبذبات ، اليمين أو اليسار. لتطبيق الأرصاد الجوية لنظام لورينز ، بعد عدد عشوائي من الأيام الصافية ، يلي عدد عشوائي من الأيام الممطرة.

ضع في اعتبارك برنامجًا لرسم خريطة لجاذ Lorentz في طائرة xyz لمعرفة الحالات الأولية المختلفة قليلاً:


تظهر نتائج البرنامج في الرسوم البيانية التالية:





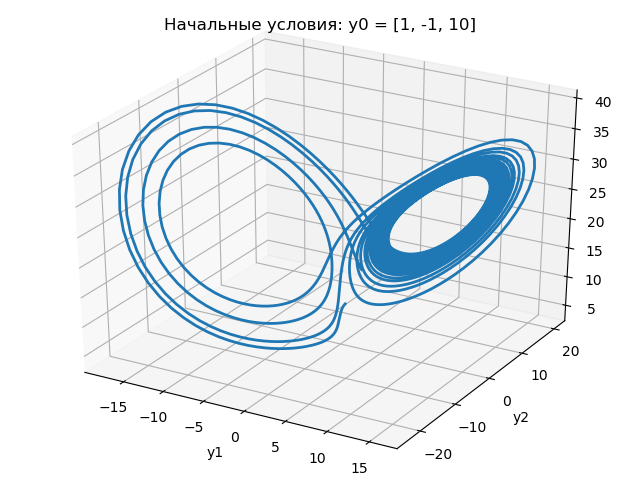
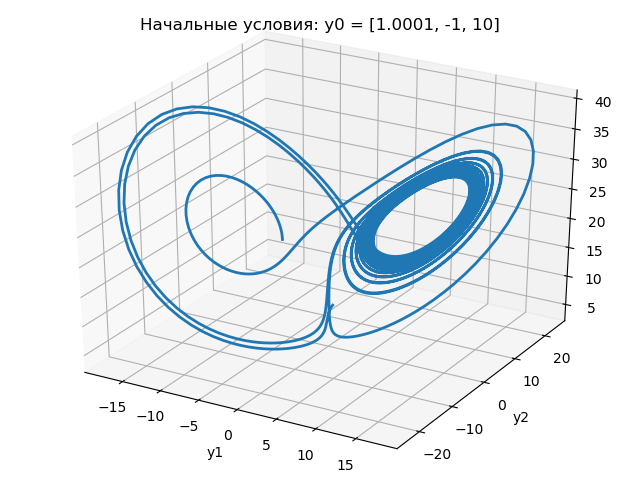
من الرسوم البيانية أعلاه ، يؤدي التغيير في الشرط الأولي من 1.0 إلى 1.0001 إلى تغيير كبير في طبيعة التغيير في جاذبية Lorentz.

نظام روسلر

هذا نظام ثلاثي الأبعاد غير خطي مدروس بشكل مكثف:
$$$\ frac {dx} {dt} = - y-z ،$
$$$\ frac {dy} {dt} = x- \ alpha y،$ (10)
$$$\ frac {dz} {dt} = b + x (x-c).$

سنقوم بكتابة برنامج للتكامل العددي للنظام (10) للمعلمات التالية a = 0.39 ، b = 2 ، c = 4 في الظروف الأولية x (0) = 0 ، y (0) = 0 ، z (0) = 0 :


نتيجة البرنامج:



في الطائرة ، يبدو شريط روسلر وكأنه حلقة ، ولكن في الفضاء ، يبدو أن الملتوية مثل شريط موبيوس.

الاستنتاجات

لإظهار ظاهرة الفوضى ، يتم تقديم برامج بسيطة وبديهية بلغة برمجة بيثون عالية المستوى ، والتي يسهل ترقيتها إلى مشاريع جديدة حول هذا الموضوع. تحتوي المقالة على تركيز تعليمي ومنهجي ويمكن استخدامها في عملية التعلم.

المراجع

1. قليلا عن الفوضى وكيفية إنشائها
2. نظرة نقدية على جاذب لورنز
3. مولدات الفوضى FPGA
4. المعادلات التفاضلية ومشاكل القيمة الحدية: النمذجة والحساب باستخدام Mathematica و Maple و MATLAB. الطبعة الثالثة.: لكل من الانجليزية - م.: شركة ذات مسؤولية محدودة "I.D. ويليامز ، 2008. - 1104 صفحة: إل. - Paral. حلمة الثدي. الإنجليزية