في الآونة الأخيرة ، تم نشر
مادة في مجلة Quanta ، تحدث فيها المؤلف عن ظاهرة كانت مفاجئة من وجهة نظر القراء عديمي الخبرة ، والتي أثبتها علماء الرياضيات. جوهرها هو أن معظم الحدود المتعددة من نوع معين غير قابلة للاختزال ، أي أنه لا يمكن تحللها. يتم تطبيق هذا الدليل في العديد من مجالات الرياضيات البحتة. ولكن هذه أيضًا أخبار سارة لأحد أركان الحياة الحديثة - التشفير الرقمي.
للتخزين الموثوق به للمعلومات الرقمية ، يتم استخدام التشفير باستخدام خوارزمية RSA على نطاق واسع. هذه نسخة مضخّمة من مخطط يمكن حتى لطلاب الصف السابع التوصل إليه لتبادل الرسائل مع الأصدقاء: يتم تعيين رقم لكل حرف ، مضروبًا بمفتاح سري مُحدد مسبقًا. لفك تشفير رسالة ، ما عليك سوى تقسيمها إلى مفتاح سري.
يعمل تشفير RSA بطريقة مماثلة. نقدم شرح مبسط للغاية. يأتي المستخدم برسالة ويقوم بتنفيذ عمليات رياضية معينة ، بما في ذلك الضرب بعدد كبير للغاية (عدة مئات من الأرقام). الطريقة الوحيدة لفك تشفير الرسالة هي إيجاد عوامل بسيطة للنتيجة *.
*العوامل الأولية للرقم هي الأعداد الأولية التي يجب ضربها للحصول على هذا الرقم. لذلك ، بالنسبة للرقم 12 ، يكون 2 * 2 * 3 ، والرقم 495 هو 3 و 3 و 5 و 11.
يعتمد أمان تشفير RSA على حقيقة أن الرياضيات لا تعرف طرقًا سريعة للعثور على العوامل الأولية بأعداد كبيرة جدًا. وإذا لم تكن الرسالة المشفرة مخصصة لك ، ولم يكن لديك مفتاح لفك تشفيرها ، فقد تستغرق محاولات العثور على هذا المفتاح آلاف السنين. علاوة على ذلك ، ينطبق هذا أيضًا على أجهزة الكمبيوتر الأكثر حداثة ، والتي لا تزال غير ممكنة تحديد العوامل البسيطة الصحيحة.
ولكن هناك حل.
يمكن تمثيل كل رقم على أنه معادلة جبرية فريدة. وخلافا للبحث عن العوامل الأولية للرقم ، فإن البحث عن العوامل الأولية في كثير الحدود أسهل بكثير. وبمجرد أن يتم تحليل كثير الحدود في هذه العوامل الأولية ، يمكن استخدام هذه المعلومات للبحث عن العوامل الأولية للرقم الأصلي.
إليك كيف تعمل.
الخطوة الأولى: اختر أي رقم تحتاج إلى معرفة عوامله الأساسية. للبساطة ، خذ الرقم 15.
الخطوة الثانية: 15 تترجم إلى الثنائية:
1111.
الخطوة الثالثة: يتحول هذا التعبير الثنائي إلى كثير الحدود من خلال ترجمة جميع الأرقام الثنائية إلى معاملات متعددة الحدود:
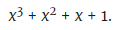
(ملاحظة: كثير الحدود هو 15 إذا كان x = 2. الرقم 2 هو أساس النظام الثنائي.)
الخطوة الرابعة: متعدد الحدود عامل:
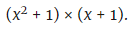الخطوة الخامسة: يتم استبدال x = 2 في كل من هذه العوامل:
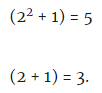الخلاصة: 5 و 3 عاملان رئيسيان في 15.
نعم ، هذه طريقة معقدة للغاية لإيجاد عوامل بسيطة لعدد صغير مثل 15 ، والتي يسهل اكتشافها في العقل. ومع ذلك ، عندما يتعلق الأمر بأعداد كبيرة تتكون من مئات الأرقام ، فإن هذه الطريقة ذات الحدود المتعددة توفر ميزة رائعة. لتحليل الأعداد الأولية ، لا توجد خوارزميات سريعة. ولكن هناك مثل هذه الخوارزميات لتحلل كثير الحدود. لذلك ، بمجرد أن تتمكن من تحويل عدد كبير إلى كثير الحدود ، يمكنك الاقتراب من العثور على عوامل بسيطة للرقم.
هل هذا يعني أن تشفير RSA في خطر؟ ليس حقا وهناك نمط جديد ثبت مؤخرًا بشأن كثير الحدود مرتبط بدقة بهذا.
أثبت عالم الرياضيات
إيمانويل بروليا وبيتر فارجو من جامعة كامبريدج أنه كلما أصبحت الحدود متعددة الحدود
للمعاملين 0 و 1 أطول ، أصبح احتمال توسيعهما أقل. وإذا كان لا يمكن تحليل متعدد الحدود ، فلا يمكن استخدامه للبحث عن عوامل بسيطة من العدد الذي يجب حسابه.
تشير أدلة Brull و Varju فعليًا إلى أن حل مشكلة تشفير RSA لا يؤدي إلى أي مكان. الأعداد الكبيرة جدا المستخدمة في RSA تتوافق مع كثيرات الحدود الطويلة جدا. يجادل علماء كامبريدج أنه يكاد يكون من المستحيل العثور على كثيرات الحدود من هذا الطول التي يمكن أن تتحلل. لطالما اشتبه كل من علماء الرياضيات وعلماء الرياضيات في أن الأمر كذلك. ومع ذلك ، عندما يعتمد الأمن السيبراني العالمي على استحالة استخدام بعض التقنيات الرياضية ، فمن الجيد دائمًا أن يكون لديك دليل على أن هذه التقنية لا تعمل حقًا.
