Biquaternions

إذا قمت بفتح هذا المقال ، فربما تكون قد سمعت بالفعل عن الأرباع ، وربما تستخدمها في تصميماتك. ولكن حان الوقت للارتقاء إلى مستوى أعلى - إلى الاحتفالات.

يقدم هذا المقال المفاهيم الأساسية حول biquaternions والعمليات معهم. لفهم أفضل للعمل مع biquaternions ، يتم عرض مثال واضح في Javascript باستخدام Canvas.

Biquaternion

إن biquaternion هو رقم مفرط الحجم وله بعد 8. في المقالات والأدب باللغة الإنجليزية يطلق عليهم "quaternion المزدوجة" ، وفي الأدب باللغة الروسية هناك أيضا أسماء "quaternion المزدوجة" أو "quaternion معقدة".

يتمثل الاختلاف الرئيسي عن quaternions في أن quaternion يصف اتجاه الكائن في الفضاء ، ويصف biquaternion أيضًا موضع الكائن في الفضاء.

يمكن تمثيل Biquaternion كربعين:

$$

$$\ widetilde {\ textbf {q}} = \ تبدأ {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix} ،$$

$$$\ textbf {q} _1$ - الجزء الحقيقي ، يحدد اتجاه الكائن في الفضاء ؛
$$$\ textbf {q} _2$ - الجزء المزدوج ، يحدد موقع الكائن في الفضاء.

يُطلق على biquaternion أيضًا رباعيات معقدة ، في هذه الحالة يتم تمثيلها على شكل رباعيات ، يكون كل مكون منها عبارة عن رقم مزدوج (يجب عدم الخلط بينه وبين المجمع). عدد مزدوج $$$A = a_1 + \ epsilon a_2$ اين $$$a_1$ و $$$a_2 دولا$ هي أرقام حقيقية ، و $$$\ epsilon$ - رمز كليفورد (التعقيد) ، حيازة الممتلكات $$$\ epsilon ^ 2 = 0$ . لن نتعمق في الرياضيات ، حيث أننا مهتمون أكثر بالجزء التطبيقي ، لذلك ، سننظر أيضًا في biquaternion كربعين.

التفسير الهندسي ل biquaternion

عن طريق القياس مع رباعي ، والتي يمكنك تعيين اتجاه الكائن ، يمكن ل biquaternion أيضا تعيين الموقف. أي يحدد biquaternion قيمتين في آن واحد - موضع الكائن واتجاهه في الفضاء. إذا أخذناهم في الديناميات ، فإن biquaternion يحدد كميتين - السرعة الخطية للحركة والسرعة الزاوية لدوران الكائن. يوضح الشكل أدناه المعنى الهندسي ل biquaternion.



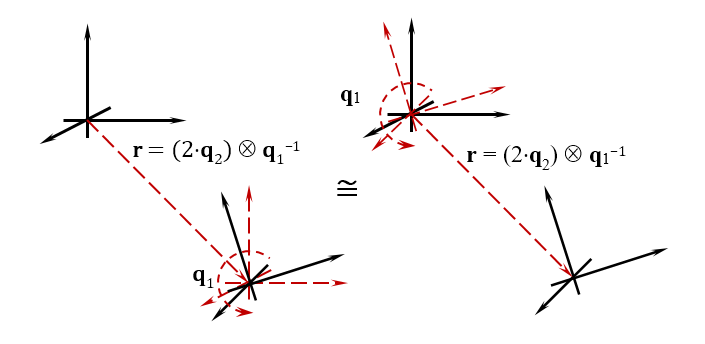
يعلم مطورو الألعاب أنه لتحديد موضع واتجاه كائن ما في مساحة اللعبة ، يتم استخدام مصفوفات الدوران ومصفوفات الإزاحة ، ووفقًا للترتيب الذي طبقته به ، تختلف نتيجة الموضع النهائي للكائن. بالنسبة لأولئك الذين اعتادوا على تقسيم الحركة إلى عمليات منفصلة ، اقبلوا قاعدة العمل مع biquaternions: أولاً ، ننقل الكائن ، ثم نديره. في الواقع ، إنك تصف هاتين الحركتين برقم واحد ، وإن كان عبارة عن hypercomplex معقدة.

الخصائص العددية

النظر في الخصائص العددية الرئيسية. من الضروري هنا الانتباه إلى حقيقة أنهم لا يعيدون الأرقام الحقيقية العادية ، ولكن الأرقام المزدوجة.

1. قاعدة biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. وحدة Biquaternion

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

العمليات الأساسية

النظر في العمليات الأساسية للعمل مع biquaternions. كما ترون ، فهي تشبه إلى حد كبير عمليات مماثلة مع الأرباع.

1. الاقتران Biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ * = \ تبدأ {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Biquaternion الجمع والطرح

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ تبدأ {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

الجمع والطرح من biquaternions أمر تبادلي (يمكن تبادلها مصطلحات).

3. ضرب العدد الحقيقي من biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ تبدأ {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Biquaternion الضرب

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ تبدأ {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

الضرب Biquaternion غير تبادلي (مع تغيير في ترتيب العوامل ، نتيجة الضرب biquaternion مختلفة).

هذه العملية هي واحدة من العمليات الرئيسية عند العمل مع biquaternions وتحمل المعنى المادي ، وهي نتيجة الضرب biquaternion هو عملية إضافة التناوب والحركات الخطية لاثنين من biquaternions.

5. عكس biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

تقرير biquaternion من خلال زوايا الاتجاه ومتجه الموقف

أولاً ، نحدد أنظمة الإحداثيات التي سننظر فيها في اتجاه الكائن وموضعه في الفضاء. يجب أن يتم ذلك لتحديد الجزء الحقيقي من biquaternion (رباعي الاتجاه) ، والذي يؤثر تسلسل دورانه على رباعي الناتج من زوايا الاتجاه. هنا سوف نسترشد بزوايا الطائرة - ياو $$$\ psi$ الملعب $$$\ vartheta$ ولفة $$$\ gamma$ .

تحديد نظام الإحداثيات الأساسي. تخيل أنك تقف على سطح الأرض وتبحث في اتجاه الشمال.

النقطة O - أصل نظام الإحداثيات ، الموجود عند نقطة أصل الكائن.
يتم توجيه المحور O _o Y _g - رأسياً إلى أعلى ، وهو عكس اتجاه ناقل الجاذبية.
يتم توجيه المحور O _o X _g - نحو الشمال ، على طول الظل من خط الطول المحلي.
محور O _o Z _g - يكمل النظام إلى اليمين ويتم توجيهه إلى اليمين ، باتجاه الشرق.

نظام الإحداثيات الثاني متصل. تخيل ، على سبيل المثال ، طائرة أو جسم آخر.
النقطة O - أصل نظام الإحداثيات ، كقاعدة عامة ، يقع عند نقطة مركز كتلة الكائن.
محور OY - موجه رأسياً لأعلى ، وعمودي على المستوى الأفقي للكائن.
محور OX - موجه إلى الأمام إلى النقطة الأمامية للكائن.
محور OZ - يكمل النظام إلى اليمين.

يتم تحديد موضع الكائن في الفضاء بواسطة ناقل نصف القطر للأصل (النقطة O ) لنظام الإحداثيات المرتبط بالنسبة لنظام إحداثيات القاعدة الثابتة. يتم تحديد اتجاه نظام الإحداثيات المرتبط بالقاعدة بواسطة ثلاث دورات متتالية على:

زاوية ياو $$$\ psi$ - الدوران حول المحور OY ،
زاوية الملعب $$$\ vartheta$ - الدوران حول المحور OZ ،
زاوية لفة $$$\ gamma$ - الدوران حول المحور OX .

لتحديد الأولي ل biquaternion ، يجب عليك تحديد الأجزاء الحقيقية والمزدوجة من biquaternion. يتم تعيين اتجاه الكائن وموضعه بالنسبة لنظام إحداثيات أساسي معين باستخدام زوايا الاتجاه $$$\ psi ، \ vartheta ، \ gamma$ وموقف المتجه من مركز الكتلة $$$r = (r_x، r_y، r_z) ^ T$ .

الجزء الحقيقي $$$\ textbf {q} _1$ يمكن ضبطها باستخدام الصيغة:

$$

$$\ textbf {q} _1 = \ start {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$$

يرجى ملاحظة أنه إذا كان لديك تسلسل دوران مختلف ، فستكون التعبيرات مختلفة أيضًا.

جزء مزدوج $$$\ textbf {q} _2$ المعرفة بالتعبير:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

حساب زوايا الاتجاه ومتجه الموقف من biquaternion. التحول العكسي

يمكن حساب زوايا الاتجاه من الجزء الحقيقي من biquaternion $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

يتم تحديد موضع الكائن بالتعبير:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

والنتيجة هي ناقل في شكل رباعي $$$\ textbf {r} = (0 ، r_x ، r_y ، r_z) ^ T$

تدوير ونقل biquaternion ناقلات

واحدة من الخصائص العظيمة ل biquaternions هو دوران وحركة ناقل من نظام إحداثي إلى آخر. اجعل O _o X _g Y _g Z _g نظام إحداثيات ثابت القاعدة ، و OXYZ يكون نظام الإحداثيات المتصل للكائن. ثم يمكن تحديد اتجاه وموضع الكائن بالنسبة لنظام الإحداثيات الأساسية بواسطة biquaternion $$$\ widetilde {\ textbf {q}}$ . إذا تم تحديد ناقل $$$\ textbf {r}$ في نظام الإحداثيات المتصل ، ثم يمكنك الحصول على ناقل $$$\ textbf {r} _0$ في نظام الإحداثيات الأساسي باستخدام الصيغة:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

والعودة:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

اين $$$\ textbf {r}$ هو ناقل في شكل biquaternion ، $$$\ textbf {r} = (1 ، 0 ، 0 ، 0 ، 0 ، 0 ، r_x ، r_y ، r_z)$

مكتبة جافا سكريبت Biquaternion

يتم تنفيذ جميع العمليات المذكورة أعلاه مع biquaternions في مكتبة جافا سكريبت ، اعتمادا على المهام الخاصة بك ، ويمكن تنفيذها في لغات البرمجة الأخرى. المهام الرئيسية للعمل مع biquaternions:

وظيفة	الوصف
DualQuaternion.dq	هيئة Biquaternion باعتبارها مجموعة من 8 أرقام
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	مُنشئ يعرّف biquaternion عن طريق تحديد الأرقام الثمانية
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	الحصول على biquaternion عن طريق تحديد اتجاه الكائن مع زوايا Euler وموجه ناقل الكائن
DualQuaternion.getEulerVector()	الحصول على زوايا أويلر وموقف ناقل من biquaternion
DualQuaternion.getVector()	الحصول على موقف متجه من biquaternion
DualQuaternion.getReal()	الحصول على الجزء الحقيقي من biquaternion (يحدد اتجاه الكائن في الفضاء)
DualQuaternion.getDual()	الحصول على الجزء المزدوج من biquaternion (يحدد موضع الكائن في الفضاء)
DualQuaternion.norm()	الحصول على معيار biquaternion كرقم مزدوج
DualQuaternion.mod()	الحصول على وحدة biquaternion كرقم مزدوج
DualQuaternion.conjugate()	الحصول على biquaternion مترافق
DualQuaternion.inverse()	الحصول على عكس Biquaternion
DualQuaternion.mul(DQ2)	الضرب Biquaternion
DualQuaternion.toString()	تحويل biquaternion إلى سلسلة ، على سبيل المثال ، للإخراج إلى وحدة التحكم التصحيح

مثال على العمل مع biquaternions

لفهم أفضل لأساسيات استخدام biquaternions كمثال ، فكر في لعبة صغيرة. تم تعيين منطقة مستطيلة - الخريطة. سفينة تطفو على خريطة ببندقية دوارة مثبتة على الخريطة. من الضروري هنا مراعاة أن نظام الإحداثيات الأساسي بالنسبة للسفينة هو نظام الإحداثيات للخريطة ، وبالنسبة للمدفع نظام الإحداثيات الأساسي هو السفينة. يتم رسم جميع الكائنات في نظام إحداثيات الخريطة وهنا سيكون من المثير للاهتمام معرفة كيف يمكنك الانتقال من نظام إحداثيات البندقية إلى نظام إحداثيات الخريطة باستخدام خاصية مضاعفة biquaternion. يتم التحكم في حركة السفينة بواسطة مفاتيح W ، A ، S ، D. يتم تعيين اتجاه البندقية بواسطة مؤشر الماوس.



يتم وصف Ship Gun : Ship Gun . في مُنشئ فئة السفينة ، يتم تعيين شكلها في شكل نقاط biquaternion ، والتوجه الأولي والموضع على الخريطة في شكل هذا this.dq_pos biquaternion.

يتم إعطاء زيادات Biquaternion أيضا لمراقبة السفينة. عند التنقل ذهابًا وإيابًا (المفاتيح W ، S) ، سيتم تغيير الجزء المزدوج فقط من biquaternion ، وعند التحكم في الجانب الأيمن الأيسر (المفاتيح A ، D) ، فإن الجزء الحقيقي والثنائي من biquaternion سيتغير ، مما يحدد زاوية الدوران.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

في الفصل نفسه ، هناك وظيفة واحدة فقط لتقديم السفينة Ship.draw() . لاحظ تطبيق عملية biquaternion لضرب كل نقطة من السفينة مع biquaternion من الموقع الحالي واتجاه السفينة.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

في مُنشئ فئة البندقية ، يتم تحديد شكلها في شكل نقاط biquaternion. سيتم عرض البندقية كخط. يتم تعيين الاتجاه الأولي والموقف على السفينة بواسطة هذا this.dq_pos biquaternion. أيضا ، يتم تعيين الربط للسفينة التي يتم تثبيتها. لا يمكن تدوير البندقية على السفينة إلا ، لذا فإن زيادة biquaternion عند التحكم في البندقية لن تؤدي إلا إلى تغيير الجزء الحقيقي من biquaternion ، والذي يحدد زاوية الدوران. في هذا المثال ، يتم توجيه التطبيق من خلال مؤشر الماوس ، وبالتالي فإن دوران البندقية سيحدث على الفور.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

في فئة البندقية ، Ship.draw() أيضًا تنفيذ وظيفة واحدة فقط لتقديم Ship.draw() . يتم عرض السلاح كخط ، والذي تم تعيينه بواسطة نقطتين this.dq_backward و this.dq_forward . لتحديد إحداثيات نقاط البندقية ، يتم استخدام الضرب biquaternion.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

يتم تنفيذ التحكم في السفن والبنادق من خلال الأحداث. أربعة متغيرات leftPressed, upPressed, rightPressed, downPressed ، والتي تتم معالجتها في حلقة البرنامج الرئيسية ، هي المسؤولة عن الضغط على مفاتيح التحكم في السفينة leftPressed, upPressed, rightPressed, downPressed .

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

واحدة من أكثر الوظائف إثارة للاهتمام ، من وجهة نظر استخدام عمليات biquaternion ، هي السيطرة على بندقية السفينة في اتجاه مؤشر الماوس. أولاً ، يتم تحديد إحداثيات مؤشر الماوس في biquaternion dq_mouse_pos . ثم ، يتم حساب biquaternion لموقف الماوس بالنسبة للسفينة باستخدام الضرب biquaternion. مأخوذة من السفينة مأخوذة من الماوس biquaternion dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(ملاحظة: عمليات الضرب المتسلسل biquaternion قراءة من اليمين إلى اليسار). وأخيراً ، يتم تحديد الزاوية بين متجهات الأداة والماوس. gun_1.dq_backward تعيين القيمة المستلمة gun_1.dq_backward نقطة بدء البندقية gun_1.dq_backward .

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

في الجزء الرئيسي من البرنامج ، gun_1 كائنات السفينة والبنادق ship_1 و gun_1 ، ويتم عرض معلومات تصحيح الأخطاء ، وتتم معالجة التحكم في السفينة.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

يحتوي رابط الأرشيف على الكود الكامل للمكتبات للعمل مع quaternions و biquaternions ، البرنامج النصي نفسه وملف index.html ، والذي يمكن فتحه محليًا في المستعرض من أجل تشغيل المثال أعلاه.

مثال على العمل مع biquaternions

الخاتمة

قد يكون لديك سؤال: لماذا تستخدم مثل هذا الجهاز الرياضي المعقد عندما يمكنك الحصول عليها من خلال الأدوات القياسية لتحريك الأجسام وتدويرها؟ واحدة من المزايا الرئيسية هي أن شكل الكتابة biquaternion هو أكثر كفاءة من الناحية الحسابية ، لأن جميع العمليات مع biquaternions بعد أن تم توسيع التعبيرات هي خطية. يُظهر هذا الفيديو ، الذي يظهر على شكل هندسي مع المزج التقريبي المزدوج الرباعي ، مدى فعالية حسابات biquaternion أكثر من الطرق الأخرى.

أخذت بشكل رئيسي معلومات حول استخدام biquaternions من مصادر إنجليزية.
من الأدب المحلي ، يمكن أن أنصح كتابين:

1. شيلنوكوف يوري نيكولاييفيتش. نماذج رباعي و biquaternion وطرق الميكانيكا الصلبة وتطبيقاتها. هندسة و حركية الحركة. - العمل النظري الضخم.
2. غورديف فاديم نيكولاييفيتش. الأرباع و biquaternions مع تطبيقات في الهندسة والميكانيكا. - مكتوب بلغة أكثر قابلية للفهم ويظهر التطبيقات في مهام تشكيل الهياكل المكانية المنحنية.