نمذجة السلاسل الزمنية

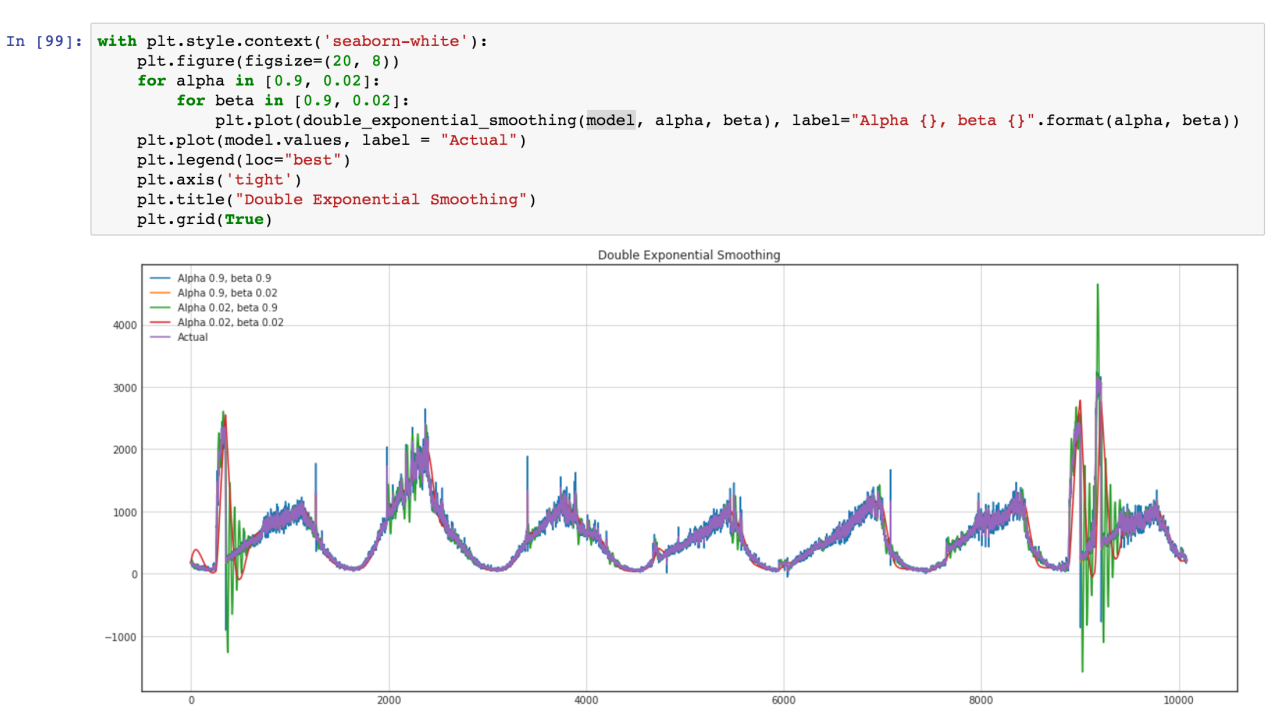
هذا مقال قصير حول فهم السلاسل الزمنية والخصائص الرئيسية وراء ذلك.

بيان المشكلة

لدينا بيانات السلاسل الزمنية مع انتظام يومي وأسبوعي. نريد أن نعرف الطريقة التي يتم بها تصميم هذه البيانات بطريقة مثالية.

تحليل السلاسل الزمنية

واحدة من الخصائص الهامة للسلسلة الزمنية هي المركزية.

في الرياضيات والإحصاء ، تعتبر العملية الثابتة (وتعرف أيضًا باسم عملية ثابتة صارمة (ly) أو عملية ثابتة (ly) ثابتة) هي عملية عشوائية لا يتغير توزيع احتمالاتها المشتركة عند تحولها في الوقت المناسب.

وبالتالي ، فإن المعلمات مثل الوسط والتباين ، إذا كانت موجودة ، لا تتغير أيضًا بمرور الوقت. نظرًا لأن الافتراض هو افتراض يستند إلى العديد من الإجراءات الإحصائية المستخدمة في تحليل السلاسل الزمنية ، غالبًا ما يتم تحويل البيانات غير الثابتة لتصبح ثابتة.

السبب الأكثر شيوعًا لانتهاك الاستقرائي هو الاتجاهات في الوسط ، والتي يمكن أن تكون إما بسبب وجود جذر الوحدة أو الاتجاه الحتمية. في الحالة الأولى من جذر الوحدة ، يكون للصدمات العشوائية آثار دائمة ، وهذه العملية لا تعود إلى الوراء. في الحالة الأخيرة من الاتجاه الحتمية ، تسمى العملية عملية ثابتة للاتجاه ، ويكون للصدمات العشوائية تأثيرات مؤقتة فقط تعود إلى الوسط (على سبيل المثال ، يعود المتوسط ​​إلى متوسطه على المدى الطويل ، والذي يتغير حتميًا مع مرور الوقت الاتجاه).

أمثلة للعمليات الثابتة مقابل العمليات غير الثابتة

خط الاتجاه



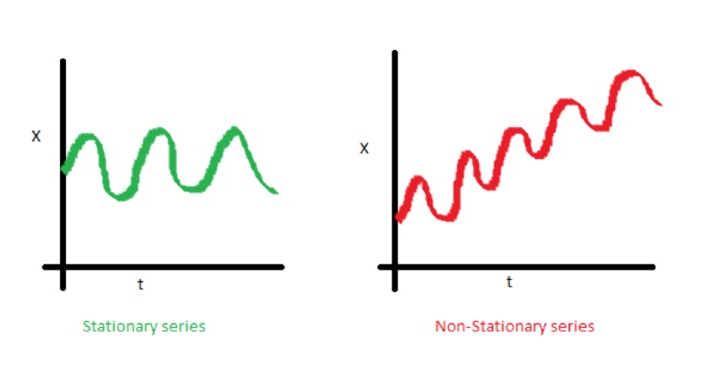
تشتت





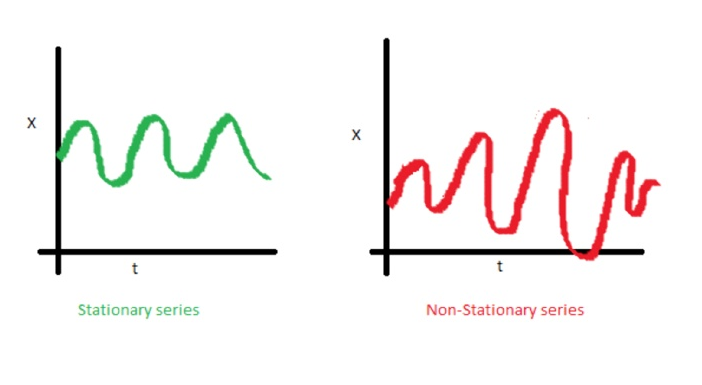
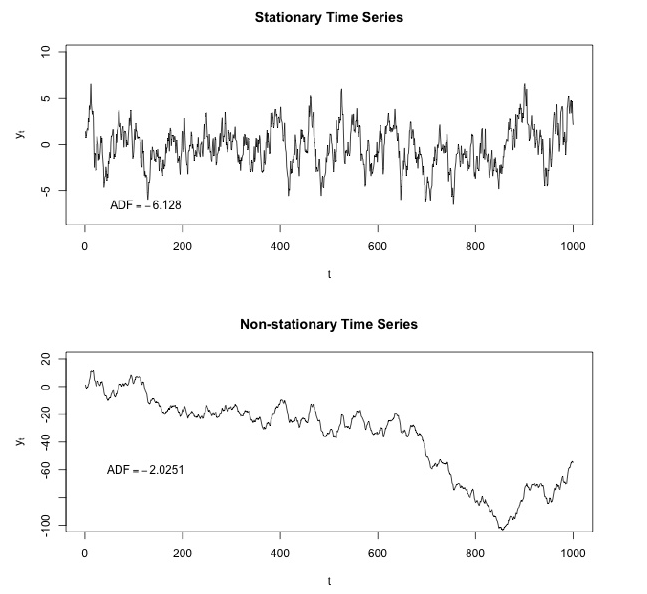
الضوضاء البيضاء هي عملية ثابتة في مؤشر ستوكاستيك يمكن وصفها باستخدام معلمتين: المتوسط ​​والتشتت (التباين). في الوقت المنفصل ، تعتبر الضوضاء البيضاء إشارة منفصلة تُعتبر عيناتها بمثابة تسلسل للمتغيرات العشوائية غير المترابطة تسلسليًا مع تباين صفري ومتغير محدود.

إذا وضعنا الإسقاط على المحور y ، يمكننا أن نرى التوزيع الطبيعي. الضوضاء البيضاء هي عملية غاوسية في الوقت المناسب.



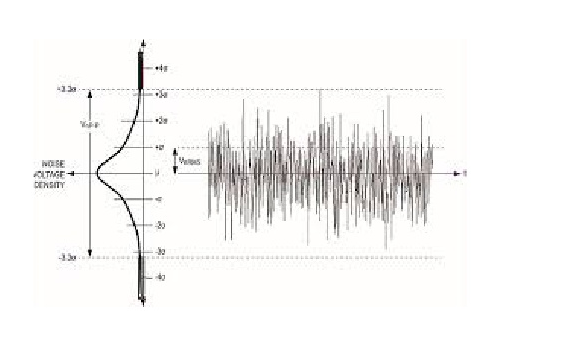
في نظرية الاحتمالات ، التوزيع الطبيعي (أو الغوسي) هو توزيع احتمالي مستمر شائع للغاية. توزيعات عادية مهمة في الإحصائيات وغالبا ما تستخدم في العلوم الطبيعية والاجتماعية لتمثيل المتغيرات العشوائية القيمة الحقيقية التي توزيعاتها غير معروفة. التوزيع الطبيعي مفيد بسبب نظرية الحد المركزي. في أكثر أشكاله عمومًا ، وفي ظل بعض الظروف (بما في ذلك التباين المحدود) ، ينص على أن متوسطات عينات ملاحظات المتغيرات العشوائية المستقاة من توزيعات مستقلة تتقارب في التوزيع إلى الطبيعي ، أي أن تصبح موزعة بشكل طبيعي عندما يكون عدد المشاهدات كبير بما فيه الكفاية. غالبًا ما يكون للكميات المادية التي يُتوقع أن تكون مجموع العديد من العمليات المستقلة (مثل أخطاء القياس) توزيعات طبيعية تقريبًا. علاوة على ذلك ، يمكن اشتقاق العديد من النتائج والطرق (مثل انتشار عدم اليقين وتثبيت معلمات المربعات الصغرى) بشكل تحليلي في شكل واضح عندما يتم توزيع المتغيرات ذات الصلة بشكل طبيعي.

نفترض أن البيانات لدينا لديها بعض الاتجاه. الطفرات المحيطة بها ترجع إلى العديد من العوامل العشوائية التي تؤثر على بياناتنا. على سبيل المثال ، يتم وصف كمية الطلبات المقدمة باستخدام هذا النهج بشكل جيد للغاية. جمع القمامة ، يخطئ ذاكرة التخزين المؤقت ، الترحيل من قبل نظام التشغيل ، والكثير من الأشياء تؤثر على وقت معين من استجابة خدمت. لنأخذ نصف ساعة من بياناتنا ، من 2017-2008 إلى الساعة 12:00 حتى الساعة 12:30. يمكننا أن نرى أن هذه البيانات لها اتجاه ، وبعض التذبذبات



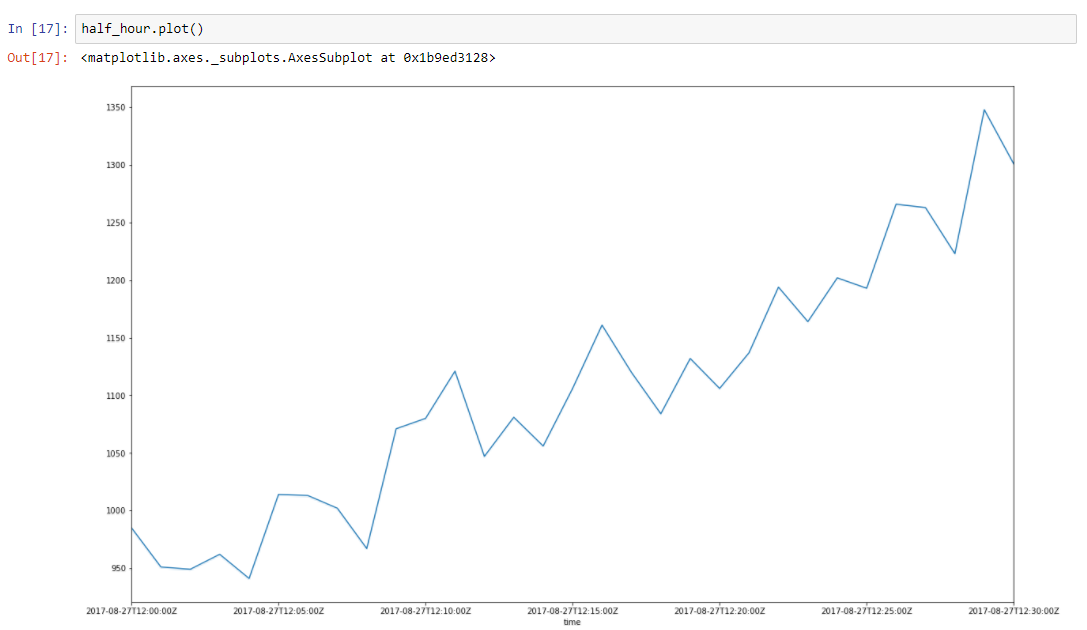
دعونا نبني خط الانحدار لتحديد ميل خط الاتجاه هذا.



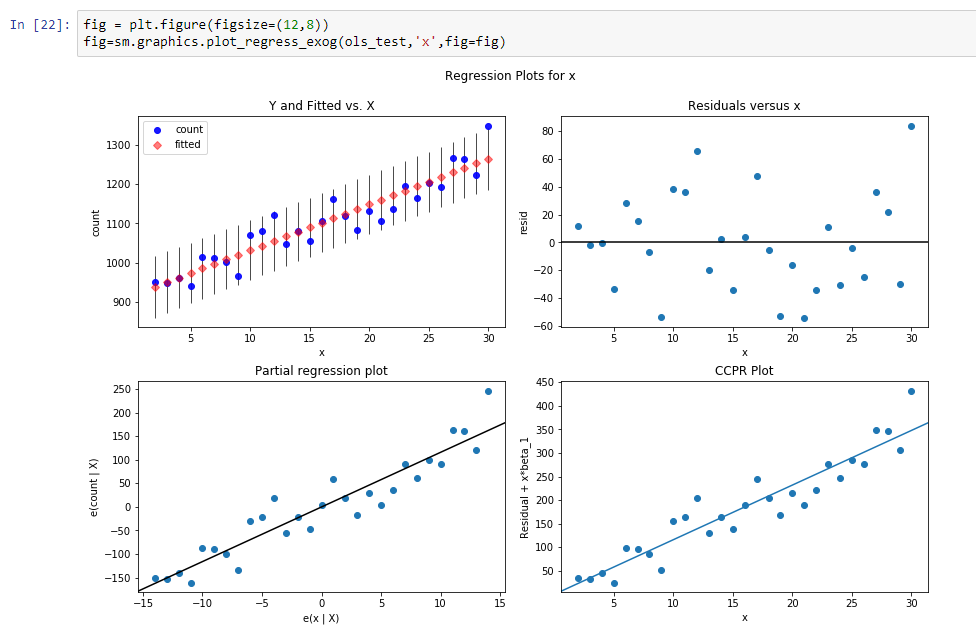
نتائج هذا الانحدار هي:

const 916.269951

dy / dx 11.599507

النتائج تعني أن const هي مستوى لخط الاتجاه هذا ، و dy / dx هو خط منحدر يحدد مدى نمو المستوى بسرعة حسب الوقت.

لذلك نحن في الواقع نخفض بعد البيانات من 31 معلمة إلى معلمتين. إذا طرحنا من بياناتنا الأولية قيمنا الدالة الانحدار سنرى العملية ، التي تبدو وكأنها عملية عشوائية مؤشر ستوكاستيك.

لذلك بعد الطرح يمكننا أن نرى أن هذا الاتجاه قد اختفى ويمكننا أن نفترض أن هذه العملية عشوائية في هذا النطاق. ولكن كيف يمكننا أن نكون متأكدين.



دعونا نجعل ديكي - اختبار أكمل .

يقوم ديكي - فولر باختبار الفرضية الفارغة المتمثلة في أن السلسلة الزمنية لها جذر وهي ثابتة كذلك أو ترفض هذه الفرضية. إذا أجرينا اختبار ديكي فولر على الشريحة الأولية ، فسنحصل عليها



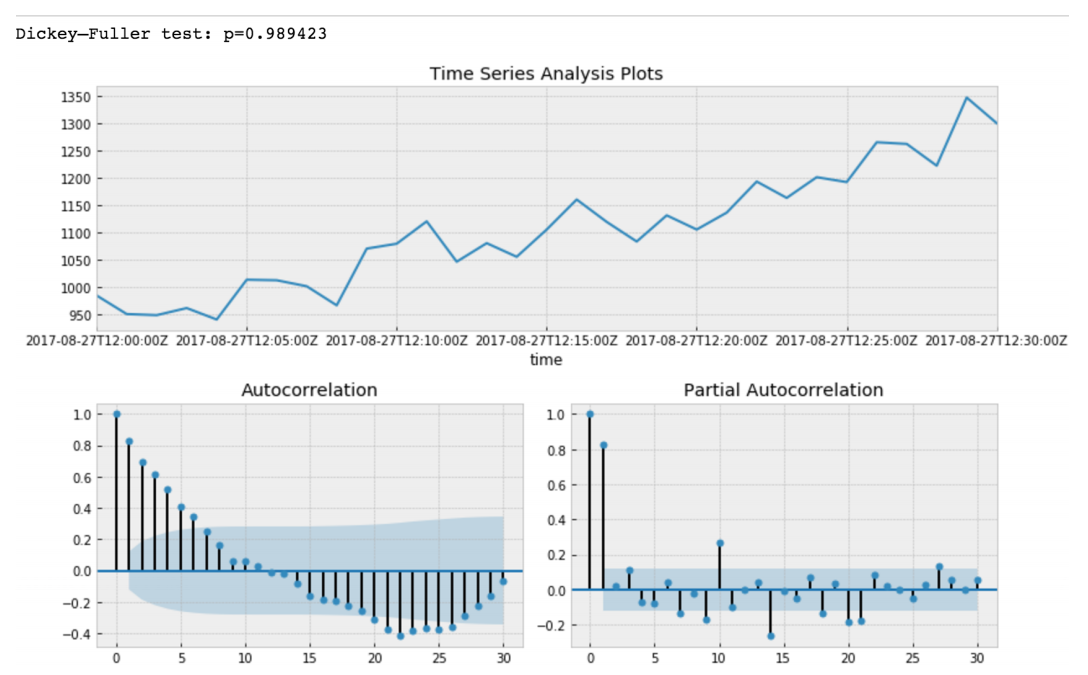
ترفض قيمة اختبار ديكي فولر فرضية لاغية بثقة قوية. وبالتالي لدينا سلسلة زمنية شريحة هي واحدة غير ثابتة. ويمكننا أن نرى أن وظيفة الارتباط التلقائي تُظهر الارتباطات المخفية.

بعد طرح نموذج الانحدار لدينا من البيانات الأولية.



هنا يمكننا أن نرى أن قيمة اختبار ديكي فولر صغيرة جدًا ولا ترفض فرضية فارغة حول عدم ثبات شريحة سلسلة زمنية لدينا. أيضا وظيفة الارتباط التلقائي تبدو جيدة.

وبالتالي ، قمنا بإجراء بعض التحولات في بياناتنا ويمكننا تدوير بياناتنا وفقًا لانحدار خط الاتجاه لدينا.

الانحدار المجزأ للبيانات

الانحدار المقسّم ، والمعروف أيضًا باسم الانحدار التدريجي أو "الانحدار المقطوع" ، هو طريقة في تحليل الانحدار يتم فيها تقسيم المتغير المستقل إلى فواصل زمنية ويتناسب مقطع سطر منفصل مع كل فاصل زمني. يمكن أيضًا إجراء تحليل الانحدار المقسّم على بيانات متعددة المتغيرات بتقسيم المتغيرات المستقلة المختلفة. يكون الانحدار المقسوم مفيدًا عندما تظهر المتغيرات المستقلة ، المتقسمة إلى مجموعات مختلفة ، علاقات مختلفة بين المتغيرات في هذه المناطق. الحدود بين القطاعات هي نقاط التوقف.

في الواقع ، يعتبر منحدرنا مشتقًا منفصلاً لسلسلة زمنية غير ثابتة نظرًا للفاصل الزمني الثابت لنقاط القياس التي لا يمكننا أخذها في الاعتبار dx. وبالتالي ، يمكننا تقريب بياناتنا كدالة متقطعة يتم حسابها باستخدام مشتقات منفصلة لاتجاهات انحدار السلاسل الزمنية.



أعلاه عبارة عن شريحة بيانات من 26–078 حتى الساعة 00.00

يبدو أن هناك ارتباطًا خطيًا تلقائيًا لكل شريحة ، وإذا وجدنا خط انحدار لكل شريحة ، فيمكننا بناء نموذج لشرائح وقتنا باستخدام افتراضات قمنا بها.

نتيجة لذلك ، سيكون لدينا بيانات موصوفة باستخدام الحد الأدنى من المعلمات وهو أمر مفضل بسبب تعميم أفضل. يجب أن يكون بُعد Vapnik - Chervonenkis صغيرًا قدر الإمكان لتعميم جيد.

في نظرية Vapnik - Chervonenkis ، يعد بُعد VC (بالنسبة إلى بعد Vapnik - Chervonenkis) مقياسًا لقدرة (التعقيد ، القدرة التعبيرية ، الثراء ، أو المرونة) لمساحة من الوظائف التي يمكن تعلمها بواسطة خوارزمية تصنيف إحصائي. يتم تعريفها على أنها أصل أكبر مجموعة من النقاط التي يمكن أن تتحطمها الخوارزمية. تم تعريفه في الأصل بواسطة فلاديمير فابنيك وأليكسي تشيرفونينكيس.

بشكل رسمي ، ترتبط قدرة نموذج التصنيف بمدى تعقيده. على سبيل المثال ، ضع في اعتبارك عتبة كثير الحدود بدرجة عالية: إذا تم تقييم الحدود متعددة الحدود فوق الصفر ، يتم تصنيف هذه النقطة على أنها موجبة ، أو سلبية. يمكن أن يكون كثير الحدود بدرجة عالية بشكل بارع ، لذلك يمكن أن يناسب مجموعة معينة من نقاط التدريب جيدًا. ولكن يمكن للمرء أن يتوقع أن المصنف سوف يرتكب أخطاء في نقاط أخرى ، لأنه بارع للغاية. مثل كثير الحدود لديه قدرة عالية. بديل أبسط بكثير هو عتبة وظيفة خطية. قد لا تتناسب هذه الوظيفة مع مجموعة التدريب جيدًا ، نظرًا لأنها ذات سعة منخفضة.

ونتيجة لذلك ، قمنا بتقريب شرائح ساعاتنا باستخدام الانحدار المقسم.



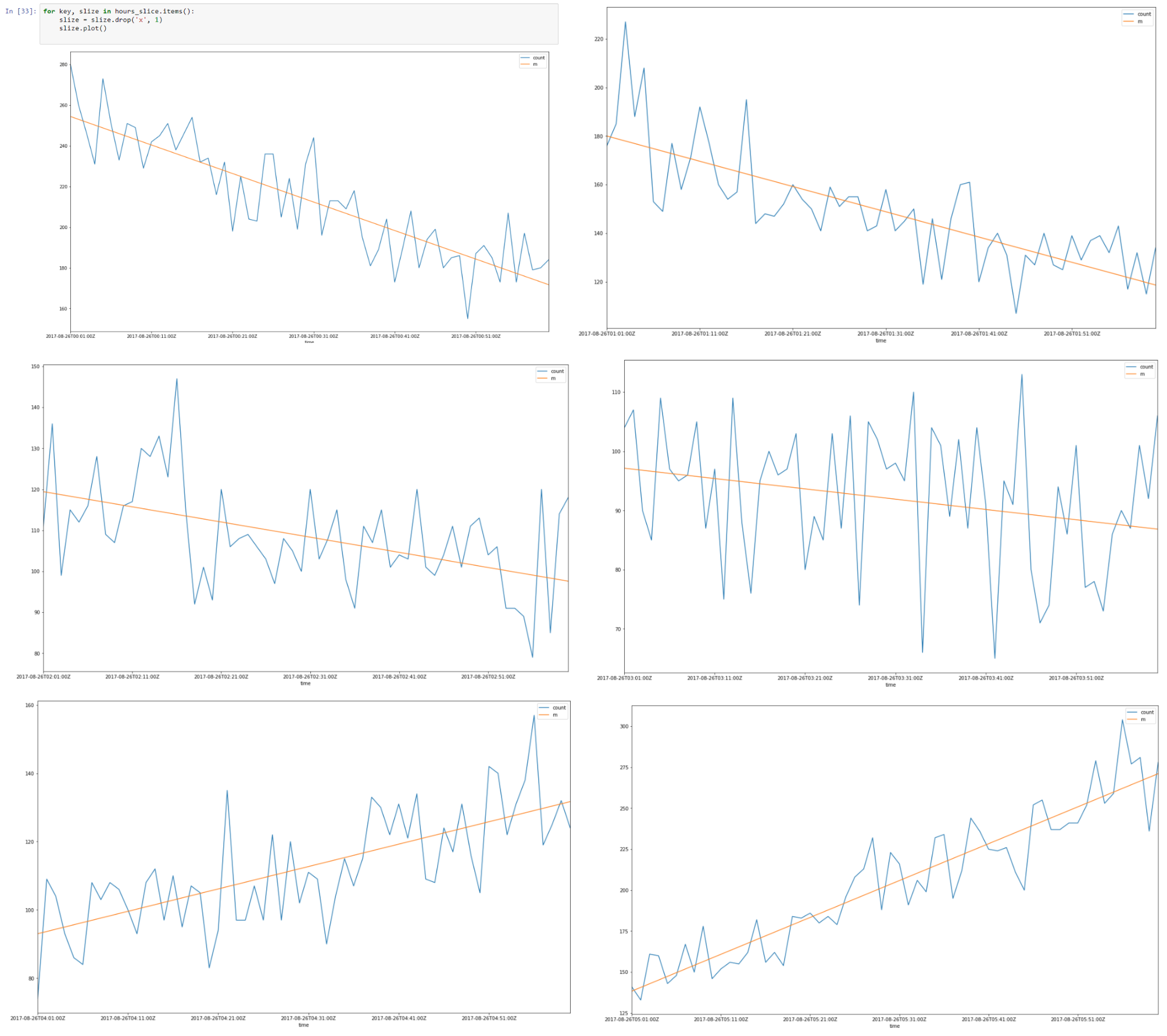
تجميع جميع شرائح 8 ساعات



وجعلها مؤشر ستوكاستيك ثابت عن طريق طرح نموذج الانحدار.



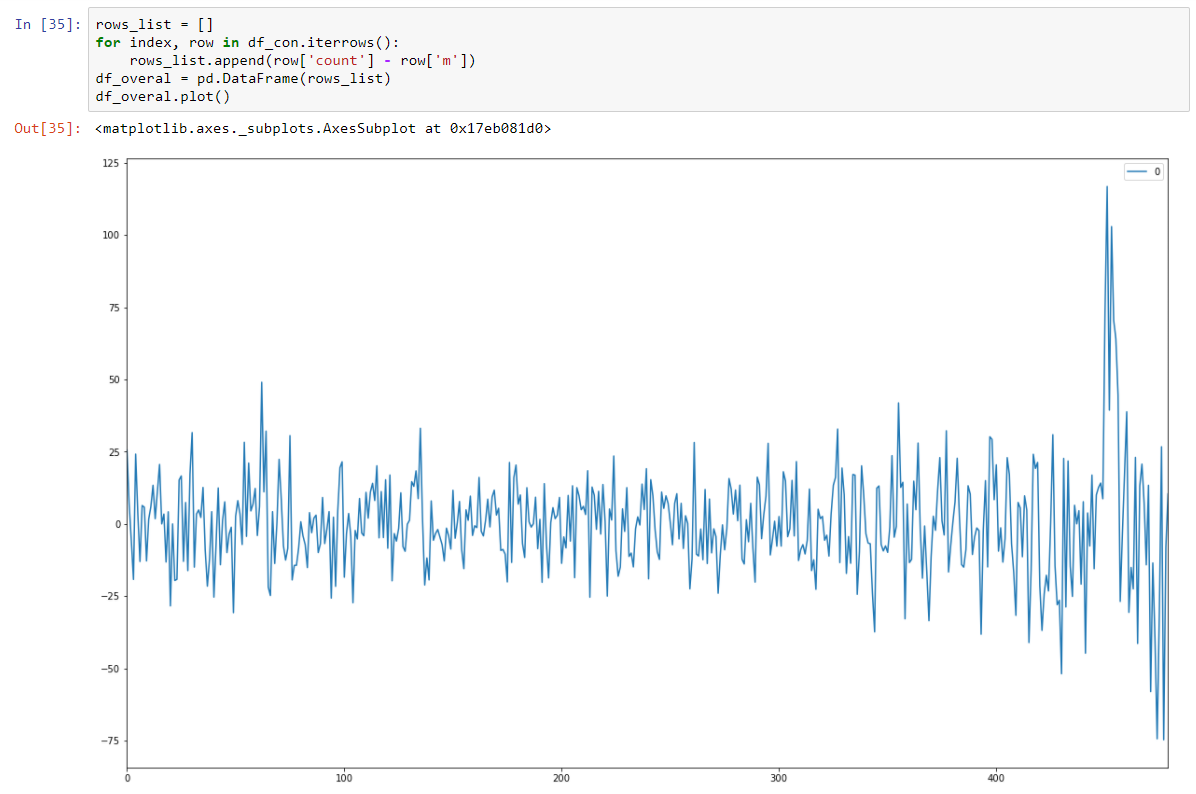
يظهر اختبار ديكي فولر الخاص بنا الثابت بثقة قوية بأننا قمنا بتحويل بياناتنا إلى سلسلة ثابتة.



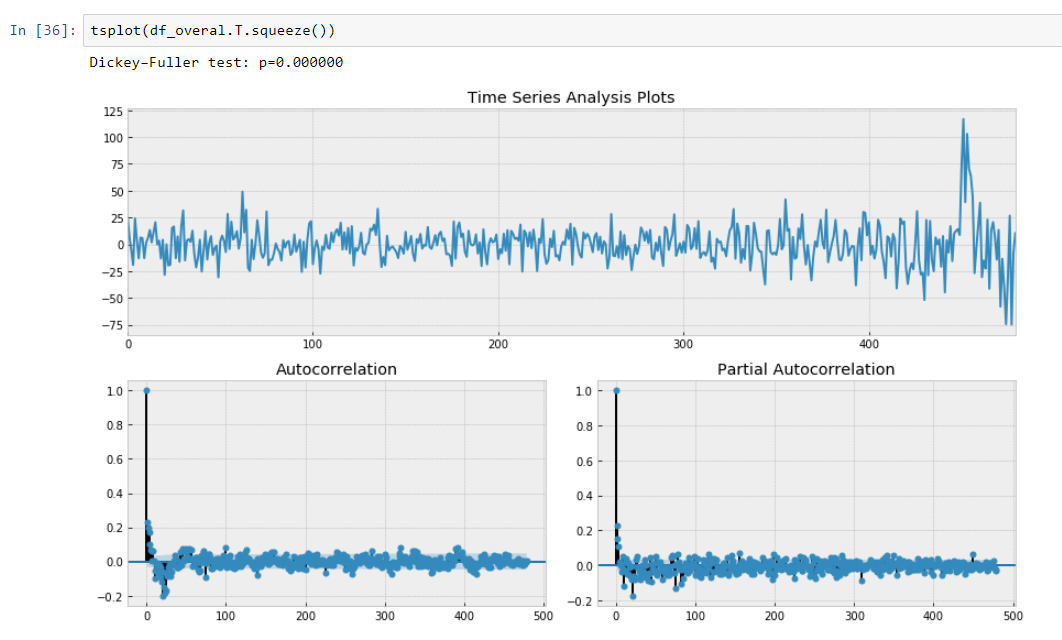
لذلك لدينا نموذج التنبؤ الذي يصف بيانات سلسلة زمنية لدينا. لقد قللنا من أبعاد بياناتنا أصغر بمقدار 15/30 مرة!

في الواقع يجب أن نرجع متوسط ​​تنبؤ نموذجنا ونحوله مرة أخرى باستخدام المستوى والمنحدر لشريحة معينة. سيؤدي ذلك إلى تقليل مجموع الأخطاء المربعة للتنبؤ بالموديلات الخاصة بنا.

ولكن يجب أن نخزن التباين أيضًا لأن الزيادة في التباين قد تؤدي إلى وجود عوامل غير معروفة جديدة وكما نعلم من معرفة المجال فإن الأمر كذلك.

التغيير السريع في التباين يجب أن يتم تنبيهك أيضًا.

نريد استخدام طراز ARIMA أيضًا ، ولكن النهج العام أكثر هو الأفضل ، ونخطط لمقارنة هذا النموذج ، و ARIMA القياسي لتحقيق نتائج أفضل. دعنا نرى سلسلة زمنية لدينا (الأخضر هي رشقات التباين على القيم المتطرفة)