تذكير
مرحبا يا هبر! أوجه انتباهكم إلى ترجمة أخرى لمقالتي الجديدة من
الوسط .
آخر مرة (
المادة الأولى ) (
Habr ) ، أنشأنا وكيلًا باستخدام تقنية Q-Learning ، التي تجري المعاملات على سلاسل زمنية محاكية وحقيقية للتبادل وحاولت التحقق مما إذا كان مجال المهام هذا مناسبًا للتعلم المعزز.
هذه المرة سنضيف طبقة LSTM لمراعاة تبعيات الوقت داخل المسار ونقوم بتكوين المكافآت بناءً على العروض التقديمية.
اسمحوا لي أن أذكرك بأنه للتحقق من المفهوم ، استخدمنا البيانات الاصطناعية التالية:
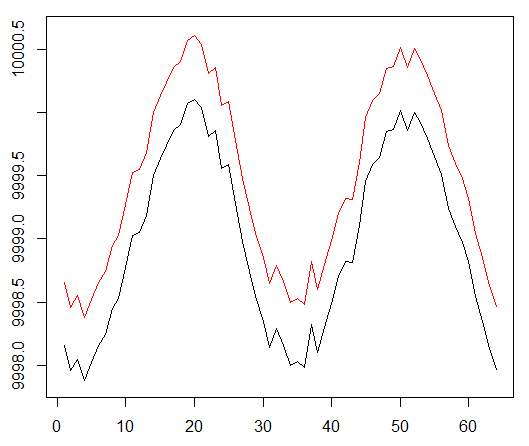
البيانات الاصطناعية: جيب مع ضوضاء بيضاء.
كانت وظيفة الجيب نقطة الانطلاق الأولى. يحاكي منحنيان سعر البيع والشراء للأصل ، حيث يكون السبريد هو الحد الأدنى لتكلفة المعاملة.
ومع ذلك ، نريد هذه المرة تعقيد هذه المهمة البسيطة من خلال توسيع مسار التنازل عن الائتمان:
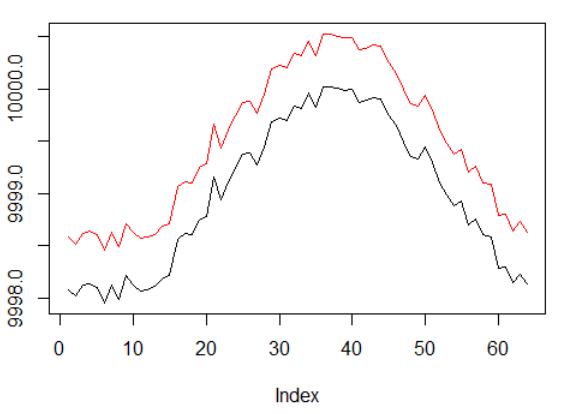
البيانات الاصطناعية: جيب مع ضوضاء بيضاء.
تضاعفت المرحلة الجيبية.
هذا يعني أن المكافآت المتفرقة التي نستخدمها يجب أن تنتشر على مسارات أطول. بالإضافة إلى ذلك ، نقوم بتقليل احتمالية تلقي مكافأة إيجابية بشكل كبير ، حيث كان على الوكيل تنفيذ سلسلة من الإجراءات الصحيحة مرتين أطول للتغلب على تكاليف المعاملات. كل من العوامل تعقيد مهمة RL إلى حد كبير حتى في ظروف بسيطة مثل موجة جيبية.
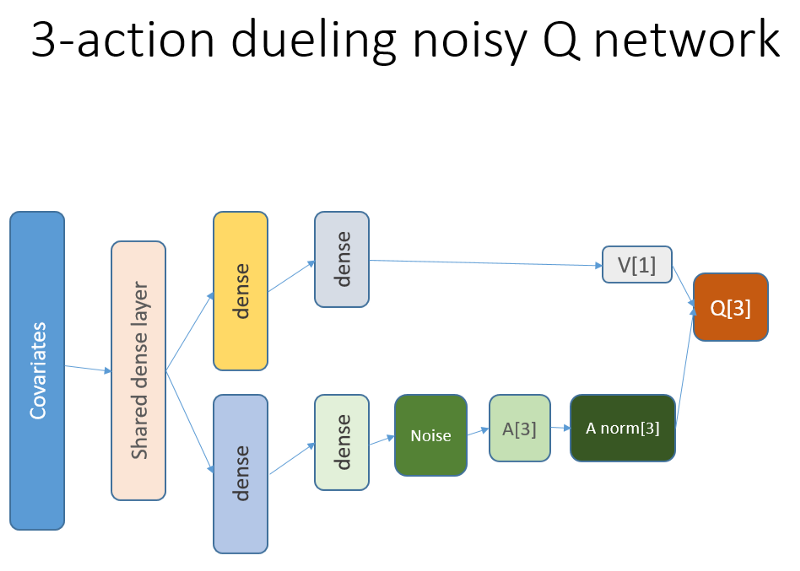
بالإضافة إلى ذلك ، نذكر أننا استخدمنا بنية الشبكة العصبية هذه:
ما تم إضافته ولماذا
Lstm
بادئ ذي بدء ، أردنا إعطاء الوكيل مزيدًا من الفهم لديناميات التغييرات داخل المسار. ببساطة ، يجب أن يفهم العميل سلوكه بشكل أفضل: ما الذي فعله الآن ولوقت ما في الماضي ، وكيف تطور توزيع تصرفات الدولة ، وكذلك المكافآت المستلمة. يمكن أن يؤدي استخدام طبقة التكرار إلى حل هذه المشكلة تمامًا. مرحبًا بك في الهيكل الجديد المستخدم لإطلاق مجموعة جديدة من التجارب:

يرجى ملاحظة أنني قد تحسنت قليلا الوصف. الفرق الوحيد من NN القديم هو أول طبقة LSTM مخفية بدلاً من طبقة مرتبطة بالكامل.
يرجى ملاحظة أنه مع LSTM في العمل ، يجب علينا تغيير اختيار أمثلة لاستنساخ تجربة للتدريب: الآن نحن بحاجة إلى تسلسل الانتقال بدلا من أمثلة منفصلة. إليك طريقة عملها (هذه واحدة من الخوارزميات). استخدمنا نقطة أخذ العينات من قبل:

المخطط وهمية من المخزن المؤقت التشغيل.
نستخدم هذا المخطط مع LSTM:

الآن يتم تحديد تسلسل (الذي نحدد طوله بشكل تجريبي).
كما كان من قبل ، والآن يتم تنظيم العينة من خلال خوارزمية الأولوية بناءً على أخطاء التعلم الزماني.
يسمح مستوى تكرار LSTM بالنشر المباشر للمعلومات من السلاسل الزمنية لاعتراض إشارة إضافية مخبأة في التأخيرات السابقة. سلسلتنا الزمنية عبارة عن موتر ثنائي الأبعاد بحجم: طول التسلسل على تمثيل حالتنا.
العروض التقديمية
الهندسة الحائزة على الجوائز ، تشكيل القدرة على المكافآت (PBRS) ، بناءً على الإمكانات ، هي أداة قوية لزيادة السرعة والاستقرار ولا تنتهك أمثلية عملية البحث عن السياسات لحل بيئتنا. أوصي بقراءة هذا المستند الأصلي على الأقل حول هذا الموضوع:
people.eecs.berkeley.edu/~russell/papers/ml99-shaping.psيحدد الجهد المحتمل مدى حالتنا الحالية بالنسبة للحالة المستهدفة التي نريد أن ندخلها. عرض تخطيطي لكيفية عمل هذا:

هناك خيارات وصعوبات يمكن أن تفهمها بعد التجربة والخطأ ، ونحذف هذه التفاصيل ، ونتركك في واجبك المنزلي.
تجدر الإشارة إلى شيء واحد آخر ، وهو أنه يمكن تبرير PBRS باستخدام العروض التقديمية ، والتي تعد شكلاً من أشكال المعرفة الخبيرة (أو المحاكاة) حول السلوك الأمثل
تقريبًا للعامل في البيئة. هناك طريقة للعثور على مثل هذه العروض التقديمية لمهمتنا باستخدام مخططات التحسين. نحذف تفاصيل البحث.
تأخذ المكافأة المحتملة الشكل التالي (المعادلة 1):
r '= r + gamma * F (s') - F (s)
حيث F هي إمكانات الدولة ، و r هي المكافأة الأولية ، gamma هي عامل الخصم (0: 1).
مع هذه الأفكار ، ننتقل إلى الترميز.التنفيذ في R
إليك رمز الشبكة العصبية استنادًا إلى واجهة برمجة تطبيقات Keras:
تصحيح قرارك بشأن ضميرك ...
النتائج والمقارنة
دعونا الغوص مباشرة في النتائج النهائية.
ملاحظة: جميع النتائج هي تقديرات نقطية وقد تختلف على فترات متعددة مع بذور بذرة عشوائية مختلفة.تشمل المقارنة ما يلي:
- الإصدار السابق دون LSTM والعروض التقديمية
- 2-عنصر بسيط LSTM
- 4-عنصر LSTM
- 4 خلايا LSTM مع المكافآت PBRS ولدت
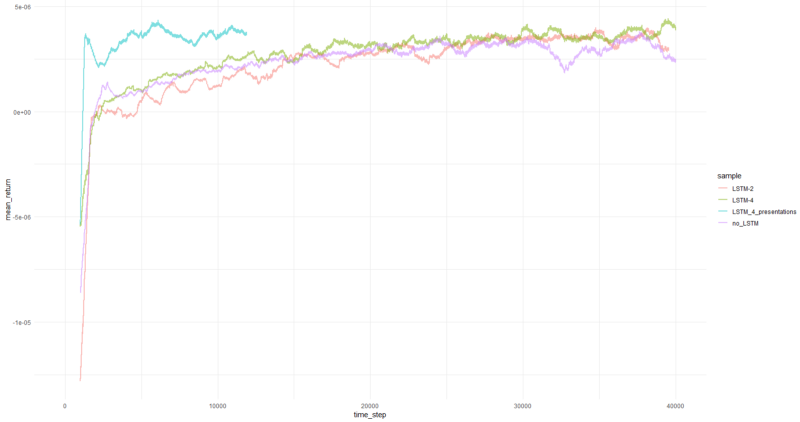
بلغ متوسط العائد لكل حلقة أكثر من 1000 حلقة.
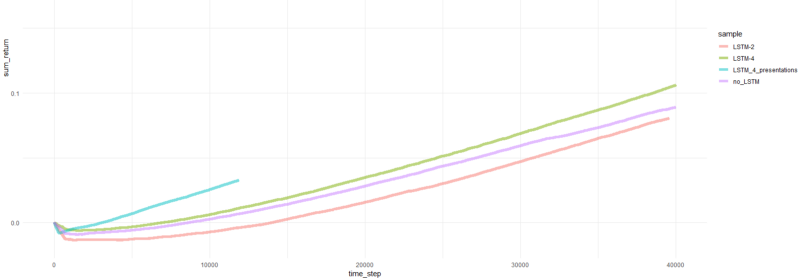
إجمالي عوائد الحلقة.
الرسوم البيانية للوكيل الأكثر نجاحا:

أداء وكيل.
حسنًا ، من الواضح تمامًا أن العامل في شكل PBRS يتقارب بسرعة وثبات مقارنة بالمحاولات السابقة التي يمكن قبولها كنتيجة مهمة. السرعة حوالي 4-5 مرات أعلى من دون العروض التقديمية. الاستقرار رائع
عندما يتعلق الأمر باستخدام LSTM ، أداء 4 خلايا أفضل من 2 الخلايا. كان أداء LSTM المكون من خليتين أفضل من الإصدار غير المعتمد على LSTM (ومع ذلك ، ربما هذا هو وهم تجربة واحدة).
الكلمات النهائية
لقد رأينا أن تكرار المكافآت وبناء القدرات يساعدان. أعجبني بشكل خاص كيف كان أداء PBRS مرتفعًا للغاية.
لا تصدق أي شخص يجعلني أقول أنه من السهل إنشاء وكيل RL يتقارب بشكل جيد ، كذبة. كل مكون جديد تمت إضافته إلى النظام يجعله أقل استقرارًا ويتطلب الكثير من التكوين والتصحيح.
ومع ذلك ، هناك أدلة واضحة على أنه يمكن تحسين حل المشكلة ببساطة عن طريق تحسين الأساليب المستخدمة (ظلت البيانات سليمة). إنها لحقيقة أن مجموعة معينة من المعلمات تعمل لأي مهمة أفضل من غيرها. مع وضع ذلك في الاعتبار ، أنت تشرع في مسار تعليمي ناجح.
شكرا لك