مرحبا بالجميع! تطوير hexapod يتقدم وأخيراً تم اختبار الجزء الرياضي الأساسي وجاهز للتوثيق. من أجل بقاء المشروع حتى النهاية وعدم تجميع الغبار على الرف ، تحتاج إلى رؤية تحولاته الإيجابية ، حتى لو كانت ضئيلة. في هذه المقالة ، سأتحدث عن خوارزمية لحل مشكلة الحركة الحركية العكسية وأظهرها أثناء العمل. آمل أن تكون مثيرة للاهتمام.
مراحل التنمية:الجزء 1 - التصميمالجزء 2 - التجمعالجزء 3 - الحركيةالجزء 4 - مسارات الرياضيات وتسلسلالجزء 5 - الالكترونياتالجزء 6 - الانتقال إلى الطباعة ثلاثية الأبعادالجزء 7 - برامج الإسكان والتطبيق الجديدة وبروتوكولات الاتصالتنسيق النظم
بادئ ذي بدء ، من الضروري تحديد أنظمة إحداثيات الروبوت - هناك ما يصل إلى ثلاثة منها:
في الواقع ، فهي لا تختلف عن بعضها البعض ، ولكنها تقع في أماكن مختلفة من القضية ، ويمكن أن تدور بالنسبة لبعضها البعض في زاوية ما. عندما يتم عرضه من الأعلى ، سيكون موقع المحاور كما يلي (سيتم وصف المعلمة coxa_zero_rotate لاحقًا قليلاً):
كما لاحظت بالفعل ، توجد أنظمة الإحداثيات على الجانبين الأيسر والأيمن متناظرة بالنسبة إلى مركز الجسم. بدا لي أنه سيكون أسهل.
يتم تعيين إحداثيات كل نقطة نسبة إلى الطرف الذي تهدف هذه النقطة. يتيح لك هذا الأسلوب تحريك الطرف دون ألم في أي مكان دون التدخل في التكوين.
وبالتالي فهي تقع نسبة إلى الطرف:
ترتبط إحداثيات النقطة الهدف بالنظام الرئيسي التنسيق. في البداية ، أردت تعيين الإحداثيات بالنسبة إلى مركز الحالة ، ولكن تبين أن هذا لم يكن مناسبًا جدًا وتطلب تخزين عدد من المعلمات الإضافية.
فيما يلي ، التدوين X * ، X ** ، إلخ. سيتم استبدال X ′ و X ′ ′.
حل المشكلة الحركية العكسية
لنبدأ بأكثر اللحظات صعوبة وإثارة للاهتمام بالنسبة لي - علم الحركة. اخترعت الخوارزمية بنفسي ، وأحيانًا ألقي نظرة على خصائص المثلث والدوال المثلثية. مع الميكانيكا ، من الصعب بالنسبة لي ، ومع علم المثلثات ، الأمر أكثر سوءًا ، لذلك ربما في مكان ما لم أستطع أخذ شيء فيه بعين الاعتبار ، لكن هذه الخوارزمية تعمل (الفيديو في النهاية).
1. بيان المشكلة
لنفترض أننا بحاجة إلى الطرف الأيمن الأمامي للوصول إلى النقطة A مع الإحداثيات (150 ؛ -20 ؛ 100). من المعروف أيضًا أن الطرف يتم تدويره بالنسبة للجسم بمقدار 45 درجة (المعلمة coxa_zero_rotate):
الطرف نفسه لديه المعلمات التالية:
أعتقد أنك لست بحاجة إلى وصف معنى هذه المعلمات ، فالأسماء تتحدث عن نفسها. يمكنك فقط إضافة أن جميع هذه المعلمات يتم تحديدها من خلال تكوين الحالة ، وهي دائمة ومخزنة في ذاكرة فلاش مع إمكانية التعديل من الخارج (للمرونة).
لهذا السبب كنت في حاجة إليها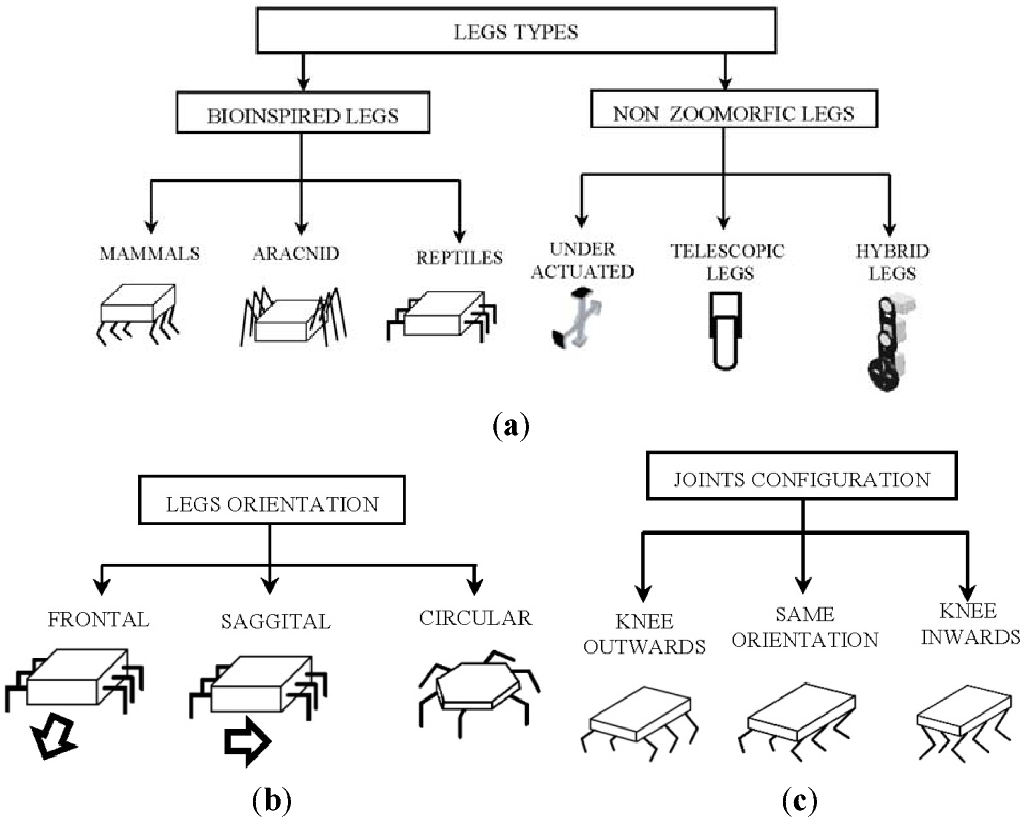
تُظهر الصورة أشكالًا مختلفة من الهيكل وموقع أرجل hexapod. الآن يطابق تكوين ARACNID. لنفترض أنه حدث لي تغيير الحالة إلى REPTILES ، ولهذا سيكون من السهل جدًا تغيير قيم المعلمات دون قياس في البرنامج نفسه ، حتى النقاط المستهدفة لن يتعين تغييرها (ما لم يكن بالطبع اقتراب هذا بشكل صحيح).
جميع المعلمات المذكورة أعلاه كافية لحل المشكلة.
2. حل المشكلة
2.1 العثور على زاوية دوران COXAهذه المرحلة هي أبسط. تحتاج أولاً إلى إعادة حساب إحداثيات النقطة A بالنسبة لنظام تنسيق الأطراف. من الواضح أنك تحتاج إلى تدوير الزاوية coxa_zero_rotate ، يمكنك القيام بذلك باستخدام الصيغ التالية:
عرض $$ $$ x ′ = x ⋅ cos (α) + z ⋅ sin (α) = 150 ⋅ cos (45) + 100 ⋅ sin (45) = 176.78 $$ عرض $$ $
y′=y=−20
عرض $$ $$ z ′ = -x ⋅ sin (α) + z ⋅ cos (α) = -150 ⋅ sin (45) + 100 ⋅ cos (45) = -35.36 $$ عرض $$ $
وبالتالي ، حصلنا على إحداثيات النقطة الهدف أ (176.78 ؛ -20 ؛ -35.36) بالنسبة لنظام تنسيق الأطراف.
يمكنك الآن العثور على زاوية COXA باستخدام وظيفة atan2:

وهكذا ، حصلنا على الزاوية التي تحتاجها لتدوير مضاعفات COXA بحيث تكون النقطة A في الطائرة X′Y ′. دعونا الآن التحقق من حساباتنا في KOMPAS 3D:
كل الحق.
2.2 العثور على زاوية دوران FEMUR و TIBIAللعثور على هذه الزوايا ، من الضروري الانتقال إلى الطائرة X′Y ′. للذهاب إلى الطائرة ، تحتاج إلى تدوير النقطة بواسطة الزاوية COXA ، والتي حسبناها مسبقًا.
عرض $$ $$ x ′ = x ′ ⋅ cos (α) + y ′ ⋅ sin (α) = 176.78 ⋅ cos (-11) + -20 ⋅ sin (-11) = 180.28 $$ display $$
y′=y=−20
لا يتغير الإحداثي
y ، لأننا ندور على طول المحور Y.
بعد ذلك ، تحتاج إلى إزالة طول COXA من الحساب ، أي نمر إلى الطائرة X′′Y ′ ′ ، لهذا نقوم بإجراء تحول للإحداثي
x ′ من النقطة بواسطة طول COXA:
x′′=x′−coxaLength=180.28−40=140.28
y′′=y′
بعد كل هذه المعالجات ، يتم تقليل الحل الإضافي للمشكلة لإيجاد الزاويتين
a و
b للمثلث:
قبل العثور على الزوايا ، تحتاج إلى العثور على الجانب الثالث C من هذا المثلث. هذه المسافة ليست سوى طول المتجه وتحسب بواسطة الصيغة:
عرض $$ $ C = \ sqrt {x ′ ′ ^ 2 + y ′ ′ ^ 2} = \ sqrt {140.28 ^ 2 + (-20) ^ 2} = 141.70 $$ عرض $$ $
الآن تحتاج إلى التحقق مما إذا كان الطرف يمكنه الوصول إلى هذه النقطة. إذا كانت C أكبر من مجموع أطوال FEMUR و TIBIA ، فلا يمكن الوصول إلى النقطة. في حالتنا ، 141.70 <141 + 85 - النقطة قابلة للوصول.
الآن نحن نعرف جميع جوانب المثلث ويمكننا إيجاد الزوايا
a و
b التي نحتاجها باستخدام نظرية جيب التمام:
a=acos(A2+C2−B2 over2AC)=72.05°
b=acos(B2+A2−C2 over2BA)=72.95°
الزوايا التي تم الحصول عليها غير قابلة للتطبيق لإطعامهم إلى الماكينات ، حيث لا يتم أخذ الموضع الأولي وزاوية ميل الخط المستقيم إلى المحور X في الاعتبار هنا ، وإذا علمنا الزوايا الأولية FEMUR و TIBIA (135 درجة و 45 درجة) ، فإن زاوية الميل C إلى المحور X لا تكون معروف. يمكنك العثور عليه باستخدام الدالة atan2 (y ′ ′ و x ′ ′):
عرض $$ $$ φ = atan2 (y ′ ′ ، x ′ ′) = atan2 (-20 ، 140.28) = -8.11 ° $$ عرض $$ $$
أخيرًا ، يمكنك حساب زاوية دوران الماكينتين FEMUR و TIBIA:


دعونا التحقق من حساباتنا:
يبدو وكأنه الحقيقة.
ملخص
الزوايا المحسوبة COXA و FEMUR و TIBIA مناسبة لتزويد الماكينات الخاصة بهم. قد تلاحظ أن زاوية COXA سالبة ، وبناءً على ذلك ، فإن السؤال الذي يطرح نفسه هو: "كيفية تحويل محرك الأقراص بمقدار -11.3 درجة؟". الحيلة هي أنني أستخدم الموضع المحايد لمضاعفات COXA كصفر منطقي ، مما يسمح للمحرك بتدوير الزوايا الموجبة والسالبة. هذا بالطبع واضح ، لكنني أعتقد أنه لن يكون من غير المناسب ذكر ذلك. سأتحدث عن هذا بمزيد من التفصيل في المقالات التالية عندما أتحدث عن تنفيذ كل ما سبق.
شفرة المصدر
كلمات كافية ، اسمحوا لي أن أرى الرمز#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI) #define DEG_TO_RAD(deg) ((deg) * M_PI / 180.0) typedef enum { LINK_COXA, LINK_FEMUR, LINK_TIBIA } link_id_t; typedef struct {
خوارزمية في العمل
ثم ، عن طريق الصدفة ، ظهر تسلسل كان يشبه إلى حد ما الرقص
PS
سأكون سعيدًا إذا كان بإمكان أي شخص تبسيط هذه الخوارزمية. لقد قمت بذلك حتى أتمكن من فهمه بعد نصف عام على سبيل المثال.