بيان المشكلة

كنت أتصفح الإنترنت في ذلك اليوم ، ولفت انتباهي شيء غريب إلى حد ما: محرك Mendocino . إنه دوار محمل احتكاك منخفض للغاية: كان للاسطوانة الأصلية أسطوانة زجاجية معلقة على إبرتين ، لكن الأحدث منها يستخدم نظام التعليق المغناطيسي. إنه محرك بدون فرش: يحتوي الدوار على بطاريات شمسية متصلة به ، مما يولد تيارًا للملفات الملفوفة حول الدوار. يدور الدوار في مجال مغناطيسي ثابت ، حيث تتعرض البطاريات الشمسية لمصدر الضوء واحدًا تلو الآخر. إنه حل أنيق إلى حد ما من الممكن إعادة إنشائه في المنزل.

إليك الفيديو الذي يشرح كيفية عمله (باللغة الروسية):


ولكن كان لهذا الفيديو فضول آخر أقوى من المحرك نفسه. في وصف الفيديو كتب ديمتري كورزفسكي: "لا يمكنك استبدال الدعم الجانبي بمغناطيس! لا تسألني عن هذا بعد الآن! "

إخلاء المسئولية: أنا لست خبيراً في الفيزياء وقد أكون مخطئًا للغاية في بعض الأمور ، لذلك نرحب بالتصحيحات.



دعونا نناقش مرة أخرى كيف يعمل نظام التعليق المغناطيسي الدوار. إذا أخذنا مغنطيسين ، فإن الإيزولين المحتمل يشبه هذا ، وهذا يتوقف على المسافة بين المغناطيس:



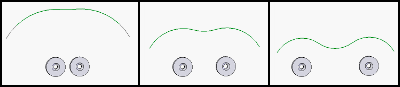
لذلك ، وضعنا اثنين من المغناطيس ثابت على الجزء الثابت. لن يرغب المغناطيس الموجود على محور الدوار في التحرك جانبيًا ، نظرًا لأن الإيزولين المحتمل يحتوي على حد أدنى محلي معين. بدلاً من ذلك ، قد ترغب في الظهور على طول محور الدوار. نحن نصنع نظامين من هذه الأنظمة ، وفي النهاية ، محور الدوران مستقر شعاعيًا ، لكنه غير مستقر بشكل جانبي. نصلح هذا عن طريق قلب الدوار على جدار زجاجي وفويلا - لدينا محامل منخفضة الاحتكاك.

لكن الجدار الزجاجي قليلاً ... ليس من الناحية الجمالية ، أليس كذلك؟ إنه لمن المنطقي فقط أن نعلق الدوران في الهواء تمامًا ، بدون عكازات ميكانيكية كهذه. ومن الواضح أن ديمتري قد تعرض للقصف بنفس السؤال أيضًا ، وهذا هو السبب في أنه كان عليه أن يشير بشكل صحيح في الوصف إلى أنه من المستحيل. وأراهن أن ديمتري ليس هو الشخص الوحيد الذي سئم من هذا.

دعنا نرى هذا ، أقتبس:

ماذا سيحدث لو كانت مغناطيس القاعدة متباعدة وموجهة في هذا الرسم؟ هل سيعطيه الثبات في المستوى المحوري ، ويلغي متطلبات المرآة؟

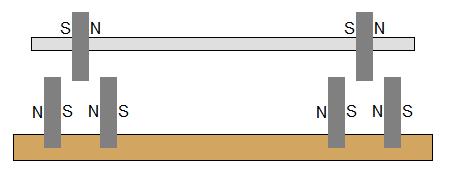
أو هنا ، أقتبس:

على Mendocino Motor ، لماذا يطفو جانب واحد مجانًا بينما يحتوي الطرف الآخر على طرف على الحائط؟ أعلم أن السؤال قد يبدو تافهاً ، لكنني قمت بفكرة عدم استخدام نفس المغناطيس المستخدم في رفع قوة المعاكس على جانبي العمود؟ أنا أرفقت jpg صعبة للغاية من ما أعنيه. المغناطيس الأخضر في نهاية الأعمدة هو ما أشير إليه. هل هناك بعض النظريات أو القوانين التي تمنع هذا؟

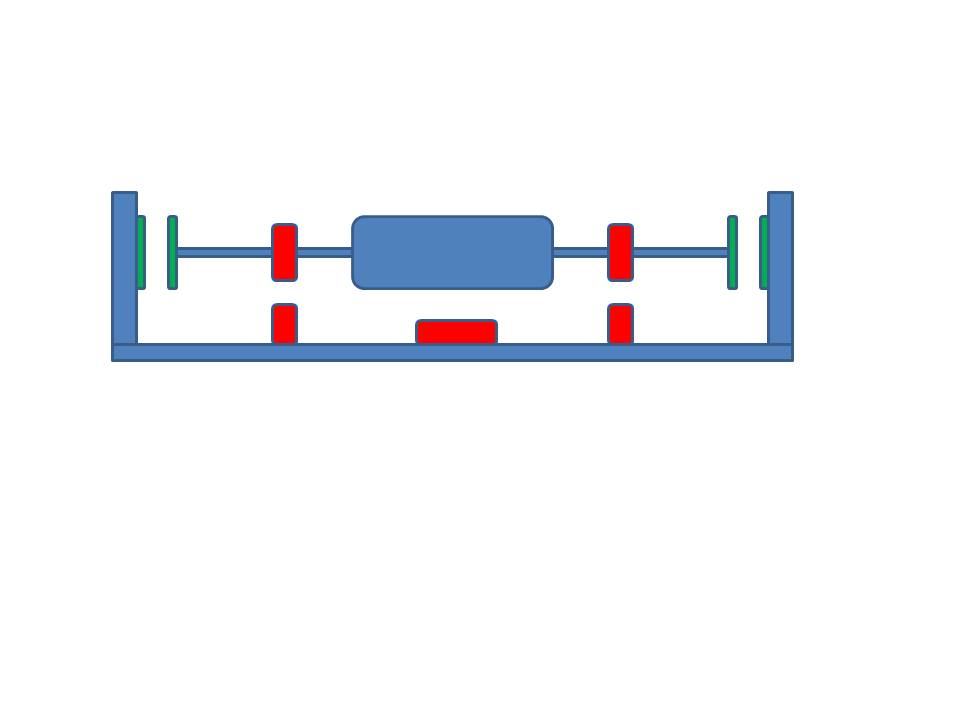
يمكننا أن نرى أن الكثير من الناس في جميع أنحاء العالم يريدون التخلص من هذا الجزء الميكانيكي غير المناسب. لم أكن أعير اهتمامًا كبيرًا في أيام دراستي ، لذلك لم يكن واضحًا على الإطلاق لماذا كان نظام التعليق المغناطيسي الثابت تمامًا غير ممكن. في أحد الأيام ، قمت بطرح هذا السؤال على المشرف ، وهو عالم مشهور (في الرياضيات التطبيقية ، وليس في الفيزياء): "لماذا هذا مستحيل؟". وأنت تعرف ماذا ، لم يكن يعرفها أيضًا!

كما أن المنتديات المنشورة أعلاه لم تقدم إجابة مناسبة على هذا السؤال. في أحسن الأحوال ، أشار شخص ما إلى ما يسمى نظرية إيرنشو ، والتي لا تتفق مع النظرة الأولى. وينص على أنه: لا يمكن الحفاظ على مجموعة من الشحنات النقطية في تكوين توازن ثابت ثابت فقط من خلال التفاعل الإلكتروستاتيكي للشحنات. هل حصلت عليه؟ بالتأكيد لم أفعل. لنفترض أنه يمكنني قبول حقيقة أننا نتحدث عن الرسوم وليس عن المغناطيس. ثم ماذا؟

التوضيح الأول

عندما لا أستطيع أن ألف رأسي حول شيء ما ، أميل إلى رسمه. دعونا توضيح هذا في 2D ، للبساطة. تخيل أربع شحنات ثابتة ، موضوعة على نمط مربع ، بالإضافة إلى شحن مجاني في الوسط. مثل هذا:



أليس الشحن المجاني في حالة توازن ، إذن؟ بغض النظر عن المكان الذي تتحرك فيه ، فإنه يقترب من إحدى الشحنات الثابتة ، مما يزيد من قوة الدفع! دعونا نحاول رسم خريطة للطاقة المحتملة لشحن مجاني. فاتني الكثير من دروس الفيزياء في المدرسة ، لذلك مستودع المعرفة الخاص بي هناك ويكيبيديا. لذلك ، إذا كان لديك شحنة واحدة ثابتة فقط ، فإنها تخلق إمكانات إلكتروستاتيكية في الحقل المحيط بها:

معادلة الإمكانات الإلكتروستاتيكية (أو Coulomb المحتملة) لشحنة نقطة في فراغ:

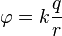
في جميع تجاربي الفكرية ، تكون كل المعاملات إما 0 أو 1. لذا q الشحنة 1 ، والمجهول k هو 1. وهذا يعني أن شحنة ثابتة واحدة تخلق طاقة محتملة تقاس 1 / r ، حيث r هي المسافة إلى تهمة.

في حالتنا ، تساوي الطاقة المحتملة للشحن المجاني داخل حقل الشحن الثابت أيضًا 1 / r. (لكي نكون منصفين ، تساوي الطاقة k * q1 * q2 / r ، لكننا نختار المعاملات لجعل العمليات الحسابية أسهل). مقابل رسوم متعددة ، نقوم ببساطة بإضافة جميع الإمكانات.

دعنا نرسم خريطة للطاقة الكامنة لدينا. أنا استخدم حكيم لهذا:

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

هناك خريطتنا. النقاط البيضاء (المثقوبة) هي حيث تذهب الطاقة الكامنة إلى ما لا نهاية:



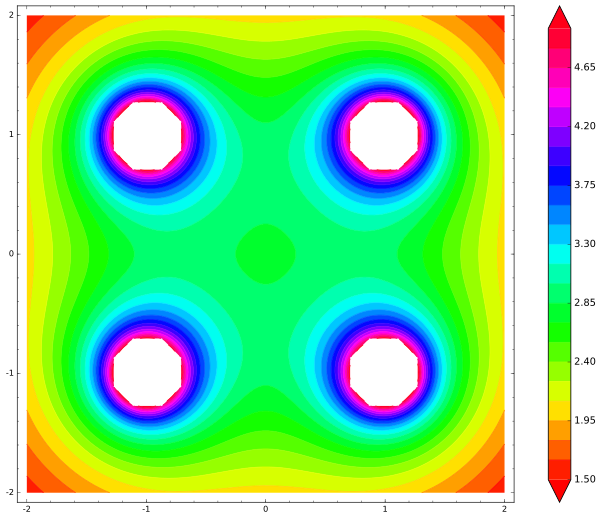
نرى بوضوح الحد الأدنى من الطاقة المحلية في المركز. أينما أراد المسؤول المركزي التحرك ، ستزداد الطاقة ، لذلك ستجبرها الاضطرابات الصغيرة على العودة إلى المركز - نقطة التوازن المستقر. كان Earnshaw خطأ ، إذن؟ لا ، لم يكن كذلك ، لقد رسم الرسم التوضيحي بشكل غير صحيح. وهذا خطأ شائع بين الأشخاص الذين يطرحون هذا السؤال. توقف لبضع دقائق الآن واحذر: ماذا فاتني؟

في الواقع ، في هذه الحالة ، كان الخطأ هو أنه في الفضاء ثنائي الأبعاد ، تخلق الشحنة الثابتة طاقة محتملة تُقاس بـ -ln r ، حيث r هي المسافة إلى الشحنة ، وليس 1 / r. فقط خذ كلمتي في الوقت الحالي واسمحوا لي بتصحيح المعادلة دون شرح الكثير. يبدو الرمز الصحيح كالتالي:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

وهذه هي الخريطة التي تنتجها:



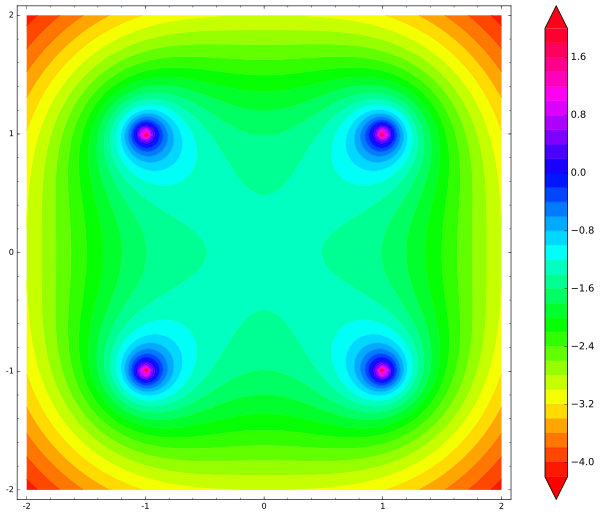
لاحظ أنه لا يوجد حد أدنى محلي في أي مكان. المركز هو نقطة السرج ، أو نقطة التوازن غير المستقر . بمجرد أن يتحرك الشحن المجاني حتى ميكرون بعيدًا عن المركز ، فإنه سيتحول حتماً خارج النظام ، ويتسارع على طول الطريق ،

انتظر لحظة ، ماذا فعلت للتو في المعادلة؟

في البداية ، عندما أدركت أن حساباتي تتناقض تمامًا مع نظرية إيرشو ، أدركت أنني ارتكبت خطأ في مكان ما. من الأسهل تتبع خطواتي منذ البداية. أخذت نفسًا عميقًا وقرأت عن معادلات ماكسويل . مرة أخرى ، لم أكن جيدًا في المدرسة: لم أكن في الصفوف (كانت هذه ممتازة) ، ولكن في مقدار المعرفة التي أخذتها منه. على سبيل المثال ، نسيت على الفور معادلات ماكسويل ، لأنه في الجامعة وخارجها لم يكن لدي أي عمل معهم.

اتضح أنها بسيطة للغاية ، خاصة إذا كنا نتحدث عن قوانين الكهرباء فقط! هناك أربع معادلات Maxwell ، واحدة لكل من هذه القوانين:

• قانون غاوس ، سنحتاجه لاحقًا. باختصار ، إنه قانون حفظ: لا يمكن توليد الطاقة من لا شيء ، ولا يمكن تدميرها.
• قانون غاوس للحقول المغناطيسية ، والذي هو في الأساس نفس الشيء. ونحن لا نذهب إلى الحقول المغناطيسية بعد ، لأننا نتحدث فقط عن الجسيمات المشحونة. تخطي هذا القانون.
• قانون فاراداي: المغناطيس المتحرك يخلق مجالًا كهربائيًا. هذا مثير للاهتمام ، سننظر إليه لاحقًا.
• قانون الامبير: تحريك المجال الكهربائي يخلق مجال مغناطيسي. عديمة الفائدة لأغراضنا.

لذلك ، تربط هذه القوانين الأربعة متجهين E و B ، المجال الكهربائي والمغناطيسي. هذه المتجهات هي وظائف ذات أربع وسيطات (x ، و y ، و z ، و t) ، وكل وسيطات أربعة يتم تقريبها مقابل متجه ثلاثي الأبعاد. نحن لسنا مهتمين بالحقول المغناطيسية ، لذلك دعونا نلقي نظرة على الحقول الكهربائية ، أو E (س ، ص ، ض ، ر). لا تنسى أننا في عالم الكهرباء الساكنة ، لذلك E ثابت عبر الزمن. يمكنك أن تتخيل هذا المتجه كنهر ، حيث في كل نقطة نقول أين وسرعة انتقال الماء.

ينص قانون فاراداي على أن حقل E الثابت للوقت (الذي نتحدث فيه عن الكهرباء الساكنة هناك) لا يحتوي على أي حليقة .

كيف يتم توصيل الكهرباء الساكنة إلى المجالات الكهربائية؟ بسيط: إذا كان الحقل E أقل تجعيدًا (كما هو الحال هناك) ، فيمكننا حينئذٍ إنشاء طريقة (العودة إلى مثال النهر) ، مغطاة بطبقة مياه طولها متر واحد (في جميع المرتفعات! ) و "الإفراج: إنه وسرعة واتجاه تدفق المياه سيخلق الحقل E. أو ، من حيث الرياضيات ، من الممكن العثور على دالة العددية ، التي يكون التدرج اللوني مساوياً للحقل E.

ينص قانون غاوس: خذ حيًا صغيرًا. إذا لم نضع الشحنات فيها عمداً ، فإن كمية "الماء" التي تتدفق إلى الحي تساوي الكمية المتدفقة. إذا كنا نريد أن نبدو أذكياء ، فإن اختلاف الحقل E يكون صفراً.

تذكر: الحقل E هو مشتق من الدالة العددية u. إذا كان انحرافها صفراً ، فهذا يعني أن laplacian u هو صفر. Laplacian هي كلمة ذكية ل "انحناء" الوظيفة. إذا كنا نتحدث عن وظائف متغيرة واحدة ، فإن اللابلاشيانية هي ببساطة المشتق الثاني. في الدالتين المتغيرين ، يكون اللابلاسيشي عبارة عن مجموع اثنين من المشتقات. إذا كان يساوي الصفر ، فيجب إلغاء الانحناء في اتجاه واحد بواسطة الانحناء في الاتجاه الآخر. المعنى ، رقائق البطاطس يمكن أن توجد:



لكن وظيفة laplacian الصفرية لا تحتوي على الحد الأدنى المحلي (أو الحد الأقصى) ، مما يعني أن رقائق البطاطس مسموح بها ، لكن التلال ليست:



تخيل غمس دائرة (منحنية) من الأسلاك في ماء صابوني. فيلم الصابون ثم يشكل سطح الصفر laplacian:



سيكون ما يسمى "الحد الأدنى للسطح". يحاول فيلم الصابون أن يكون صغيرًا قدر الإمكان ، لذلك من المنطقي أنه إذا كان لديه حد محلي معين ، فسنحصل على فيلم أصغر عن طريق تجانسه ، لذلك لا يوجد أي فيلم. لذا ، فإن الإمكانات الإلكتروستاتية هي نوع من الحد الأدنى للسطح الذي لا يحتوي على الحدود القصوى المحلية (طالما لم نضع الشحنات هناك عمداً).

وظيفة 1 / r لها laplacian صفر في ثلاثة أبعاد ، ولكن ليس في اثنين! إذا أردنا استخلاص أمثلة ثنائية الأبعاد ، فسنحتاج إلى حل مشكلة Dirichlet - بالنسبة للثنائي الأبعاد ، إنها - ص.

إن استخدام صيغة المربعات العكسية في الفضاء ذي البعد 1- أو 2 يقابل تقييد حركة الشحنات على طول المحاور المتبقية بطريقة أخرى. في هذه الحالة ، من الواضح أنه من الممكن إجراء تكوين مستقر - ما عليك سوى أخذ أنبوب من الورق المقوى ووضعه عموديًا ووضع المغناطيس. بعد ذلك ، من الممكن وضع مغناطيس إضافي واحد سيكون في حالة توازن - يتم تقييده أفقيًا بواسطة الأنبوب (أي أنه في مساحة أحادية البعد) ، وعلى قوة رأسية من الجاذبية وتنافر المغناطيس. يجب أن يتم تطبيق نظرية Earnshaw مع قانون المربعات العكسية - ولكن في الأبعاد الثلاثية ، أو في الفضاء ذي البعد ، ولكن مع الإمكانات المقابلة. "المقابلة" تعني التي تم الحصول عليها من معادلات ماكسويل.

نظرية إيرنشو ونتائجها

لذلك ، نعود إلى مثالنا مع جسيم واحد مشحون مجانا. لا تحتوي إمكانات الحقل الإلكتروستاتيكي على الحد الأدنى المحلي ، ونتيجة لذلك ، فإن الطاقة الكامنة في الجسيمات لا تحتوي على حد أدنى محلي. لذلك لا يمكن أن تصل جسيم واحد إلى توازن ثابت في مجال ثابت. تهانينا ، لقد أثبتنا نظرية Earnshaw. ولكن ماذا عن الأنظمة الأكثر تعقيدًا؟ كيفية تطبيق نظرية هناك؟

إليكم مثالًا آخر ، وفقًا لرئيسي ، يجب أن نصل إلى نظرية Earnshaw. دعنا نصلح شحنتين وننشئ جسمًا متحركًا يتألف من عصا غير قابلة للوزن أقل مع شحنات من كلا الطرفين:



بشكل حدسي ، إذا حركنا العصا قليلاً إلى اليسار أو اليمين ، فستقترب إحدى النهايات من الشحنات الثابتة ، والتي ستدفعها بعيدًا وتعيد العصا إلى الموضع الأصلي. إذن ما هي الفائدة؟ لنرسم خريطة للإمكانات الإلكتروستاتيكية لشحنتين ثابتتين:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

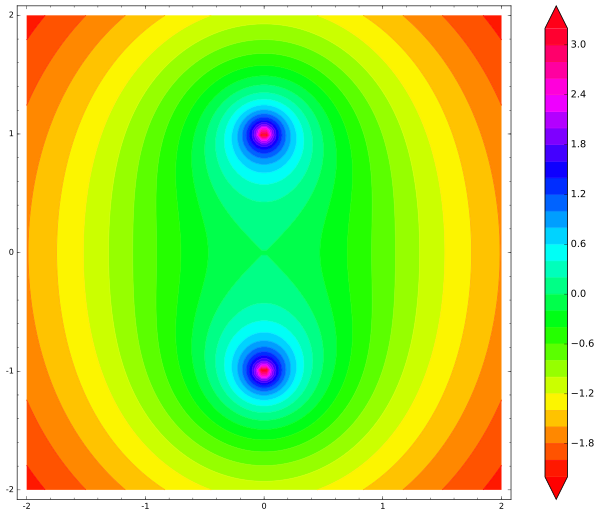
كيف نوضح الطاقة الكامنة لعصنا؟ تتمتع العصا بثلاث درجات من الحرية (درجتان للحركة وواحدة للدوران) ، لذلك سيكون الرسم البياني ثلاثي الأبعاد. دعنا نتجاهل التدوير في الوقت الحالي ودع العصا فقط تتحرك جنبًا إلى جنب. نصلح نقطة على عصا (على سبيل المثال ، مركزها) ونرسم خريطة الطاقة المحتملة للعصا لمركزها. في هذه الحالة ، فإن إجمالي الطاقة الكامنة للعصا هو مجموع الطاقات المحتملة لشحناتها على كلا الطرفين:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

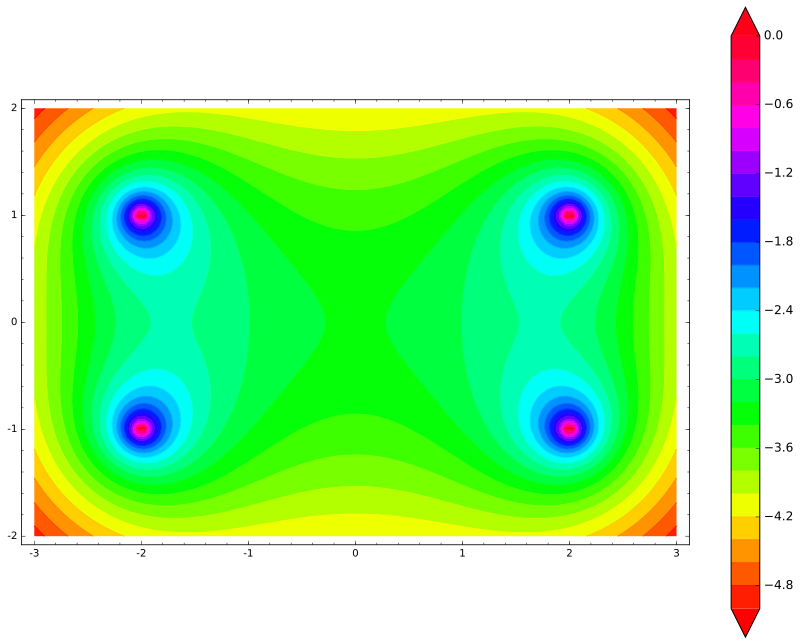
لذا ، فإن طاقة العصا لها أربعة قمم (يمكن أن تصل كل نهاية إلى كل شحنتين). كما هو متوقع ، لن تتحرك العصا أفقياً - بدلاً من ذلك ، سوف تتحرك رأسياً!

إنه منطقي فقط ، منذ كيف حصلنا على الطاقة؟ أضفنا الطاقات المحتملة لكل تهمة. نحن نعلم أن الطاقة الكامنة لكل شحنة هي وظيفة صفرية. مجموعها ، وبالتالي ، لديه أيضا laplacian الصفر. لذلك ، لا يمكن أن يكون للطاقة الكامنة لأي جسم مشحون (وليس فقط عصانا!) الحد الأدنى في مجال كهربائي ثابت!

الخاتمة

الصور البديهية للمجالات المغناطيسية والكهربائية للأشخاص الذين لا يعملون عن كثب في الفيزياء يمكن أن تكون مضللة. يخدعنا دماغنا بجعل صور الحد الأدنى من الطاقة. لسوء الحظ ، الأمر ليس كذلك ، وإنشاء محرك Mendocino دون دعم ميكانيكي أمر صعب للغاية ، إن لم يكن مستحيلاً.

ما الثغرات الموجودة لاستغلالها؟ تنطبق نظرية إيرنشو (إذا طبقناها على المغناطيس) فقط على أنظمة المغناطيس الثابت الثابت .

1. يمكننا إنشاء مجال مغناطيسي ديناميكي.
2. كما لا تندرج الديامة المغناطيسية والموصلات الفائقة تحت نظرية إيرنشو.
3. لا تناقش الأجسام المتحركة (وبالتحديد ، الأجسام الدوارة) على الإطلاق ، حيث يعتبر الليفيترون أكثر الأمثلة شهرة.

لا ، هذا ليس ميئوسا منه. بالتأكيد ، فإن استخدام أي من هذه الثغرات سيقتل جماليات محرك Mendocino ، لكن سحر أي شيء معدني يرتفع بحرية من شأنه أن يتفوق على كل ذلك!

الملاحظة الأخيرة: كانت نظرية إيرنشو هي التي أثبتت عدم وجود مادة صلبة ، وبالتالي دحض النموذج المقبول للذرة ، مما أدى إلى نموذج الذرة "الكوكبي".