😐 🧕 🦌 مهمة N الهيئات أو كيفية تفجير مجرة دون مغادرة المطبخ 👨‍🚀 🙊 🧑‍🤝‍🧑

منذ وقت ليس ببعيد قرأت رواية الخيال العلمي "مشكلة الجسد الثلاثة" لليو كيو شين . في ذلك ، واجه بعض الأجانب مشكلة - لم يعرفوا كيف ، بدقة كافية بالنسبة لهم ، لحساب مسار كوكبهم الأصلي. على عكسنا ، فقد عاشوا في نظام من فئة ثلاث نجوم ، و "الطقس" على هذا الكوكب يعتمد بشدة على موقعهم النسبي - من حرارة الحرق إلى البرد الجليدي. وقررت التحقق مما إذا كنا نستطيع حل هذه المشاكل.

فيزياء الظاهرة

لفهم المشكلة ، من الضروري التعامل مع فيزياء هذه الظاهرة. في إطار النظرية الكلاسيكية ، يتم تحديد القوة الجذابة لهيئتين بموجب قانون نيوتن :

$\ vec {F} (\ vec {r} _1 ، \ vec {r} _2) = - G m_1 m_2 \ frac {\ vec {r} _1 - \ vec {r} _2} {| \ vec {r} _1 - \ vec {r} _2 | ^ 3} ،$

اين

$\ vec {r} _1 ، \ vec {r} _2$ - موقف الهيئات في الفضاء ،

$m_1 ، m_2$ - كتل الجثث ،

$G$ - ثابت الجاذبية.
في نظام

$N$ سوف تتأثر الأجسام الموجودة على كل منها بقوة الجذب من الباقي ، والتي يتم التعبير عنها بالمعادلة:

$\ vec {F} _n = -G \ sum_ {k \ neq n} m_n m_k \ frac {\ vec {r} _n - \ vec {r} _k} {| \ vec {r} _n - \ vec {r } _k | ^ 3}.$

باستخدام قانون نيوتن الثاني ، نكتب تسارع كل جسيم:

$\ vec {a} _n = \ vec {F} _n / m_n = -G \ sum_ {k \ neq n} m_k \ frac {\ vec {r} _n - \ vec {r} _k} {| \ vec { r} _n - \ vec {r} _k | ^ 3}.$

إذ تشير إلى أن التسارع هو مشتق الإحداثي للمرة الثانية ، نحصل على معادلة تفاضلية جزئية من الدرجة الثانية ، والتي يجب حلها للحصول على مسار كل جسم:

$\ frac {\ جزئية ^ 2 \ vec {r} _n} {\ جزئية t ^ 2} = f_n = -G \ sum_ {k \ neq n} m_k \ frac {\ vec {r} _n - \ vec {r } _k} {| \ vec {r} _n - \ vec {r} _k | ^ 3}.$

من المهم أن نلاحظ هنا أن تعقيد حساب وظيفة

$f_n$ يساوي

$O (N ^ 2)$ ويزيد بشكل كبير مع زيادة عدد الهيئات المتفاعلة.

الرياضيات

الطريقة الأولى والأبسط لحل المعادلات التفاضلية هي طريقة أويلر ، المصممة لحل معادلات الشكل:

$\ frac {dy} {dx} = f (x، y).$

عند الانتقال إلى المنطقة المنفصلة ، نحصل على:

$y_ {i} = y_ {i-1} + h f (x_ {i-1} ، y_ {i-1}) ، \ quad i = 1،2،3 ، \ dots ، m ،$

اين

$ح$ هي خطوة التكامل ، و

$م دولا$ - عدد خطوات التكامل. وبالتالي ، إذا كنا بحاجة لحساب موقف الهيئات في وقت واحد

$T$ ثم يجب علينا القيام به

$m = T / h$ خطوات التكامل. هنا المشكلة الأولى واضحة - إذا

$T$ كبيرة ، ثم نحن بحاجة إلى اتخاذ عدد كبير من خطوات التكامل.

لتطبيق طريقة Euler على مشكلتنا ، يجب تخفيضها إلى نظام من الدرجة الأولى. للقيام بذلك ، نقدم متغير إضافي - سرعة الجسيمات:

$\ frac {\ جزئية \ vec {v} _n} {\ جزئية t} = f_n، \\ \ frac {\ جزئي \ vec {r} _n} {\ جزئية t} = \ vec {v} _n.$

المشكلة الثانية في حل أنظمة المعادلات التفاضلية هي دقة الحل والتحكم فيه. يمكن تحسين الدقة بطريقتين: عن طريق تقليل خطوة التكامل واختيار طريقة ذات ترتيب أعلى من الدقة. كلتا الطريقتين تؤدي إلى زيادة التعقيد الحسابي ، ولكن بطرق مختلفة. على سبيل المثال ، يمكنك استخدام الأسلوب Runge-Kutta الكلاسيكي من الدرجة الرابعة ؛ فهو يتطلب أربعة عمليات حسابية

$f_n$ في كل خطوة ، ولكن لديه ترتيب الدقة

$O (h ^ 4)$ (للمقارنة ، طريقة أويلر لديها ترتيب من الدقة

$O (h)$ ويتطلب حساب واحد

$f_n$ ) يمكن أيضًا التحكم في دقة الحل بعدة طرق: مقارنة مع الحل التحليلي ، والحل باستخدام طرق مختلفة أو بخطوات مختلفة ومقارنة النتائج ، والتحكم في معلمات الطرف الثالث والقيود التي يجب أن يتوافق معها الحل.
أيضا ، كل من هذه الأساليب لها عيوبها. قد تكون القرارات التحليلية غائبة ، أو حتى في معظم الحالات ، غائبة تمامًا. على سبيل المثال ، لمهمتنا

$N$ الحل التحليلي الهاتف هو فقط ل

$N = 2 دولا$ ، ولكن حتى هذا يكفي لاختبار دقة الأساليب. يعمل حل المشكلة بطريقتين أو بخطوات مختلفة على زيادة وقت الحساب ، ولكن يمكن تطبيق هذا النهج على أي مهمة تقريبًا. ليس لكل مهمة قيود ، ولكن بالنسبة لنا نحن لدينا هذه القيود: في كل خطوة من خطوات التكامل يمكننا التحكم في تنفيذ قوانين الحفظ . هذا النهج يزيد أيضًا من تعقيد الحساب ، ولكن هناك الكثير للاختيار من بينها ؛ حساب مجموع العزم أو العزم الزاوي لجميع الجزيئات له تعقيد الترتيب

$O (N)$ ، في حين أن حساب إجمالي الطاقة لنظام لديه تعقيد النظام

$O (N ^ 2)$

ملاحظة على حساب إجمالي الطاقة

في حالتنا ، تتكون الطاقة الكلية للنظام من جزأين - الطاقة الحركية والمحتملة. تتكون الطاقة الحركية من مجموع الطاقات الحركية لجميع الأجسام. لحساب الطاقة الكامنة ، نحتاج إلى إضافة الطاقات المحتملة لكل جسيم في حقل الجاذبية للجزيئات المتبقية ، لذلك نحن بحاجة إلى إضافة

$O (N ^ 2)$ شروط. تكمن الصعوبة في أن جميع المصطلحات ذات ترتيب مختلف تمامًا ، وحتى مع الحسابات المزدوجة الدقة ، لا يمكن حساب هذه القيمة بدقة كافية للمقارنة في خطوات مختلفة. للتغلب على هذه المشكلة ، كان من الضروري تطبيق الجمع وفقًا لخوارزمية كاهان .

الشكل 1. مثال على مسار بيضاوي الشكل.

تأمل الحالة البسيطة لقمر صناعي يتحرك في مدار بيضاوي حول الأرض. مع اقتراب القمر الصناعي من الأرض ، تزداد سرعته ، وعند الابتعاد عن الأرض يتناقص ، وبالتالي ، تنشأ احتمالية تقليل خطوة التكامل في الوقت المناسب في الجزء الأخضر من المدار ، وزيادته باللونين الأحمر والأزرق دون تغيير دقة الحل. دعنا نحاول المقارنة بمزيد من التفاصيل.

الجدول 1. طرق التحقيق لحل المعادلات التفاضلية

ملحوظ	ترتيب	الوصف
آدمز	1-5	طريقة آدمز - باشفورت
أويلر	1	طريقة أويلر
rk4	4	طريقة رانج كوتا الكلاسيكية
rkck	5	طريقة كاش كارب
rkdp	5	طريقة دورمان الأمير
rkdverk	6	طريقة فيرنر 1) ص. 181
rkf	7	فيلبرج الأسلوب 1) ص. 180
rkgl	6	طريقة غاوس ليجند الضمنية
rklc	4	طريقة Lobatto الضمنية
أرجوحة	2	شبه منحرف الطريقة

لتحديد أفضل طريقة لمهمتنا ، سنقوم بمقارنة عدة طرق معروفة. للقيام بذلك ، نقوم بمحاكاة تصادم نظامين من الهيئات

$N = 512 دولا$ وقياس التغير النسبي في إجمالي الطاقة والزخم ولحظاته في نهاية المحاكاة (أقصى وقت للمحاكاة

$T_ {max} = 2.5 دولا$ ) في هذه الحالة ، سوف نقوم بتغيير الخطوة ومعلمات طرق التكامل وقياس عدد استدعاءات الوظائف

$f_n$ ، على التوالي ، تلك الطرق التي تؤدي إلى عدد أقل من المكالمات التي تؤدي إلى انخفاض الخسارة ، وسوف نعتبر أكثر قبولا.


أ)	ب)
الشكل 2. التغير النسبي في الطاقة أ) ، الزخم ب) ، في نهاية محاكاة النظام $N = 512 دولا$ الهيئات بطرق مختلفة اعتمادا على عدد العمليات الحسابية $f_n$ دقة مزدوجة

من الرسوم البيانية في الشكل 2 ، يمكن ملاحظة أن أفضل نسبة لمقدار حساب الوظيفة

$f_n$ والتغير النسبي في طاقة نظام الهيئات في أساليب آدمز ودورمان برنس من الدرجة الخامسة. كما لوحظ أنه لجميع الطرق مع زيادة في عدد الحسابات

$f_n$ التغيير النسبي في زخم النظام يزيد. من أجل حدوث تغيير نسبي في الطاقة ، يكون هذا ملحوظًا أيضًا ، ولكن فقط لعدة طرق يمكن أن تصل إلى العتبة

$dE / E_0 <10 ^ {- 12}$ . لا يمكن أن يعزى هذا التأثير إلى خطأ الطرق ، ولكن إلى خطأ العمليات الحسابية ، وزيادة أخرى في الدقة ممكنة فقط مع زيادة في دقة العمليات الحسابية ذات النقطة العائمة.


أ)	ب)
الشكل 3. التغير النسبي في الطاقة أ) ، الزخم ب) ، في نهاية محاكاة النظام $N = 512 دولا$ الهيئات بطرق مختلفة اعتمادا على عدد العمليات الحسابية $f_n$ بدقة رباعية (__float128)

يوضح الشكلان 3 أ و 3 ب أن استخدام الحسابات ذات الدقة الرباعية يمكن أن يقلل من خسائر الطاقة النسبية حتى

$10 ^ {- 23}$ ، ولكن عليك أن تفهم أن وقت الحساب يزداد بأمرين من الحجم مقارنة بالدقة المزدوجة. كما هو الحال في العمليات الحسابية المزدوجة الدقة ، فإن أفضل نسبة للدقة وعدد حسابات الوظائف

$f_n$ تمتلك أساليب من الدرجة الخامسة آدمز ودورمان الأمير.

تنتمي أساليب Dorman-Prince و Werner إلى فئة الأساليب المتداخلة ويمكنها في نفس الوقت حساب حلين بترتيب عالٍ ومنخفض من الدقة (بالنسبة لطريقة Dorman-Prince ، المادتان 5 و 4 ، وطريقة Werner ، المادتان 6 و 5). إذا كان هذان الحلان مختلفان تمامًا ، فيمكننا تقسيم خطوة التكامل الحالية إلى حلول أصغر. يسمح لنا ذلك بتغيير خطوة التكامل ديناميكيًا والحد منها فقط في المناطق التي تتطلبها.

دعنا نقارن طرق Dorman-Prince و Werner و Adams ذات الترتيب الخامس بمزيد من التفصيل ، على مدى فترة محاكاة أطول لنظامنا (

$T_ {max} = 300 دولا$ )

أ) التغير النسبي في الطاقة والزخم واللحظة في عملية النمذجة

ب) عدد العمليات الحسابية

$f_n$ على فاصل المحاكاة

$\ دلتا تي = 0.3 دولا$

الشكل 4. تبعات التغيير النسبي في المعلمات المادية للنظام وعدد حسابات الوظائف

$f_n$ من وقت لآخر النمذجة مع طريقة الخطوة المتغيرة Dorman-Prince

$h = 10 ^ {- 5} \ dots 10 ^ {- 9}$

أ) التغير النسبي في الطاقة والزخم واللحظة في عملية النمذجة

ب) عدد العمليات الحسابية

$f_n$ على فاصل المحاكاة

$\ دلتا تي = 0.3 دولا$

الشكل 5. تبعيات التغيير النسبي في المعلمات المادية للنظام وعدد حسابات الوظائف

$f_n$ مقابل نمذجة الوقت بطريقة فيرنر مع خطوة متغيرة

$h = 10 ^ {- 5} \ dots 10 ^ {- 9}$

الشكل 6. التغير النسبي في الطاقة والزخم ولحظاته في عملية النمذجة باستخدام طريقة Adams-Bashfort من الدرجة الخامسة مع خطوة

$h = 10 ^ {- 6}$

الشكل 7. تبعيات عدد العمليات الحسابية

$f_n$ لطرق آدمز ودورمان برينس و فيرنر من الدرجة الخامسة من وقت المحاكاة

يمكن ملاحظة أنه في المرحلة الأولى من تطور نظامنا (

$T <25 دولا$ ) توضح الطرق الثلاث خصائص متشابهة ، ولكن في مراحل لاحقة تحدث أحداث معينة في النظام ، ونتيجة لذلك تقفز بشكل حاد الأخطاء في المعلمات الرئيسية للنظام (إجمالي الطاقة والزخم وزخمها). لكن طريقتي Dorman-Prince و Werner تتعاملان بشكل أفضل مع هذه التغييرات نظرًا للقدرة على تقليل خطوة التكامل في الأقسام "المعقدة" ، مما يؤدي إلى زيادة عدد حسابات الوظائف

$f_n$ كما هو مبين في الشكلين 4 ب و 5 ب ، ولكن العدد الإجمالي للحسابات

$f_n$ الأساليب المتداخلة أصغر من طريقة Adams-Bashfort ، كما يتضح من الشكل 7.

وأتساءل ماذا حدث للنظام في هذه اللحظات

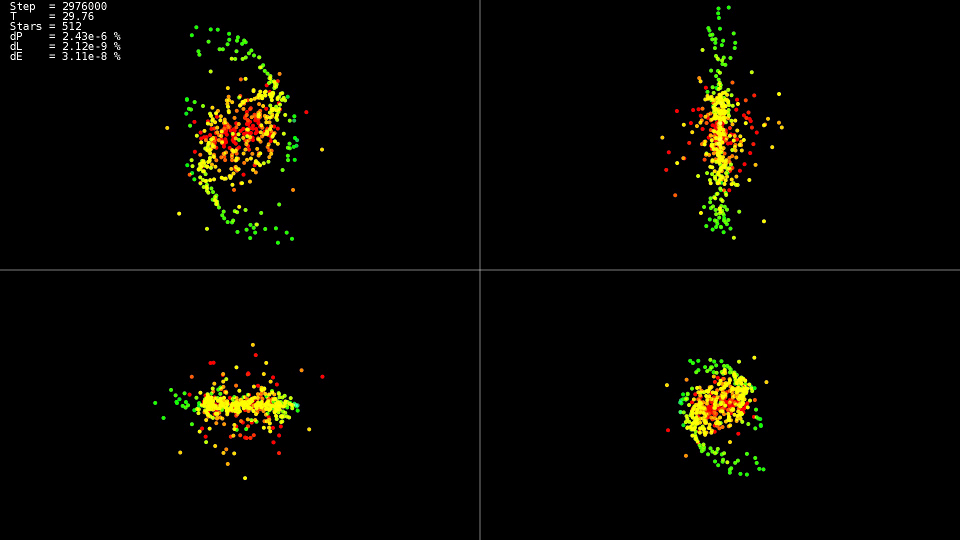
فيديو 1. نمذجة نظام من 512 جثة. طريقة دورمان الأمير. خطوة ديناميكية

$h = 10 ^ {- 5} \ dots 10 ^ {- 9}$

يوضح الفيديو ذلك حتى الوقت المناسب

$T = 25 دولا$ الحركة هادئة نسبيًا ، وبعد ذلك تصادم مراكز "المجرات" ، مما يؤدي إلى تغيير حاد في المسارات وزيادة قوية في سرعات بعض الجسيمات. علاوة على ذلك ، للحفاظ على دقة الحل ، من الضروري تقليل خطوة التكامل. يمكن للطرق المتداخلة القيام بذلك تلقائيًا ؛ توضح الرسوم البيانية أنه في بعض أجزاء تطور النظام ، تم تقليل خطوة التكامل بحوالي أمرين من حيث الحجم

$10 ^ {- 5}$ قبل

$h = 10 ^ {- 7}$ . عند استخدام طريقة آدمز ومثل هذه الخطوة على كامل الفاصل الزمني لتطور النظام ، لم ننتظر الحل.

ملخص

بالنسبة للحل ، من الأفضل استخدام الأساليب المتداخلة التي تتيح لك التحكم في خطوة التكامل ديناميكيًا ، وتقليلها فقط في الأقسام "المعقدة" من المسار.

لا تطارد أعلى أساليب الترتيب. حتى عند استخدام نوع البيانات "مزدوج" ، فإنها لا تصل إلى إمكاناتها المحتملة ، باستخدام أنواع البيانات بدقة أكبر يزيد بشكل كبير من الوقت الذي يستغرقه لحل المشكلة.

تنفيذ وحدة المعالجة المركزية

الآن وقد تم تحديد اختيار طريقة لحل المعادلات ، دعونا نحاول معرفة حساب قوة التفاعل لكل جسيم. نحصل على دورة مزدوجة لجميع الجزيئات:

كود التنفيذ "بسيط"

for(size_t body1 = 0; body1 < count; ++body1) { const nbvertex_t v1(rx[ body1 ], ry[ body1 ], rz[ body1 ]); nbvertex_t total_force; for(size_t body2 = 0; body2 != count; ++body2) { if(body1 == body2) { continue; } const nbvertex_t v2(rx[ body2 ], ry[ body2 ], rz[ body2 ]); const nbvertex_t force(m_data->force(v1, v2, mass[body1], mass[body2])); total_force += force; } frx[body1] = vx[body1]; fry[body1] = vy[body1]; frz[body1] = vz[body1]; fvx[body1] = total_force.x / mass[body1]; fvy[body1] = total_force.y / mass[body1]; fvz[body1] = total_force.z / mass[body1]; }

يتم احتساب قوى الجاذبية لكل جسم بشكل مستقل ، ولكي تستخدم جميع مراكز المعالج ، يكفي كتابة توجيه OpenMP قبل الدورة الأولى:

قطعة من التعليمات البرمجية من تنفيذ 'openmp'

 #pragma omp parallel for for(size_t body1 = 0; body1 < count; ++body1)

بسبب يتفاعل كل جسم مع كل منهما ، ثم لتقليل عدد تفاعلات المعالج مع ذاكرة الوصول العشوائي وتحسين استخدام ذاكرة التخزين المؤقت ، لدينا القدرة على تحميل جزء من البيانات في ذاكرة التخزين المؤقت واستخدامها بشكل متكرر:

رمز التنفيذ "openmp + block"

 #pragma omp parallel for for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE) { nbcoord_t x1[BLOCK_SIZE]; nbcoord_t y1[BLOCK_SIZE]; nbcoord_t z1[BLOCK_SIZE]; nbcoord_t m1[BLOCK_SIZE]; nbvertex_t total_force[BLOCK_SIZE]; for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; x1[b1] = rx[local_n1]; y1[b1] = ry[local_n1]; z1[b1] = rz[local_n1]; m1[b1] = mass[local_n1]; } for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE) { nbcoord_t x2[BLOCK_SIZE]; nbcoord_t y2[BLOCK_SIZE]; nbcoord_t z2[BLOCK_SIZE]; nbcoord_t m2[BLOCK_SIZE]; for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { size_t local_n2 = b2 + n2; x2[b2] = rx[local_n2]; y2[b2] = ry[local_n2]; z2[b2] = rz[local_n2]; m2[b2] = mass[n2 + b2]; } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { const nbvertex_t v1(x1[ b1 ], y1[ b1 ], z1[ b1 ]); for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { const nbvertex_t v2(x2[ b2 ], y2[ b2 ], z2[ b2 ]); const nbvertex_t force(m_data->force(v1, v2, m1[b1], m2[b2])); total_force[b1] += force; } } } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; frx[local_n1] = vx[local_n1]; fry[local_n1] = vy[local_n1]; frz[local_n1] = vz[local_n1]; fvx[local_n1] = total_force[b1].x / m1[b1]; fvy[local_n1] = total_force[b1].y / m1[b1]; fvz[local_n1] = total_force[b1].z / m1[b1]; } }

يتمثل التحسين الإضافي في إخراج محتويات وظيفة حساب القوة في الدورة الرئيسية والقضاء على الانقسام والضرب في كتلة الجسم m1 [b1]. إلى جانب حقيقة أننا قمنا بتقليل العمليات الحسابية قليلاً ، سيتمكن المجمّع من تطبيق إرشادات المتجه لمعالج SSE و AVX على هذه الدورة الموسعة.

كود التنفيذ 'openmp + block + optimization'

 #pragma omp parallel for for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE) { nbcoord_t x1[BLOCK_SIZE]; nbcoord_t y1[BLOCK_SIZE]; nbcoord_t z1[BLOCK_SIZE]; nbcoord_t total_force_x[BLOCK_SIZE]; nbcoord_t total_force_y[BLOCK_SIZE]; nbcoord_t total_force_z[BLOCK_SIZE]; for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; x1[b1] = rx[local_n1]; y1[b1] = ry[local_n1]; z1[b1] = rz[local_n1]; total_force_x[b1] = 0; total_force_y[b1] = 0; total_force_z[b1] = 0; } for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE) { nbcoord_t x2[BLOCK_SIZE]; nbcoord_t y2[BLOCK_SIZE]; nbcoord_t z2[BLOCK_SIZE]; nbcoord_t m2[BLOCK_SIZE]; for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { size_t local_n2 = b2 + n2; x2[b2] = rx[local_n2]; y2[b2] = ry[local_n2]; z2[b2] = rz[local_n2]; m2[b2] = mass[n2 + b2]; } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { nbcoord_t dx = x1[b1] - x2[b2]; nbcoord_t dy = y1[b1] - y2[b2]; nbcoord_t dz = z1[b1] - z2[b2]; nbcoord_t r2(dx * dx + dy * dy + dz * dz); if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = (m2[b2]) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; total_force_x[b1] -= dx; total_force_y[b1] -= dy; total_force_z[b1] -= dz; } } } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; frx[local_n1] = vx[local_n1]; fry[local_n1] = vy[local_n1]; frz[local_n1] = vz[local_n1]; fvx[local_n1] = total_force_x[b1]; fvy[local_n1] = total_force_y[b1]; fvz[local_n1] = total_force_z[b1]; } }

الجدول 2. تبعية وقت الحساب (بالثواني) للدالة

$f_n$ على عدد من الهيئات المتفاعلة

$N$ لمختلف تطبيقات وحدة المعالجة المركزية

$N$	2048	4096	8192	16384	32768
بسيط	0.0425	0.1651	0.6594	2.65	10.52
openmp	0.0078	0.0260	0.1079	0.417	1.655
openmp + block + التحسين	0.0037	0.0128	0.0495	0.194	0.774

معلمات النظام:

النظام: ديبيان 9 ، إنتل كور i7-5820K (6 كور)
مترجم: مجلس التعاون الخليجي 6.3.0

من الواضح أن الإصدار الذي يدعم OpenMP يتم تسريعه بستة أضعاف ، بالضبط من حيث عدد النوى ، والإصدار الأمثل أسرع بأكثر من مرتين بقليل. لذلك ، مع التحسين ، يجب أن لا تعتمد فقط على التزامن. ومن المثير للاهتمام ، في الحسابات أحادية الدفق ، أن المعالج قد عمل بتردد 3.6 غيغاهرتز ، وفي الإصدار الموازي (openmp) أسقط التردد إلى 3.4 غيغاهرتز ، وفي التوازي والمحسّن (openmp + block + الأمثل) ، انخفض إلى 3.3 غيغاهرتز ، ولكن هذا لم يمنعها من العمل 13.6 مرة أسرع. يُرى أيضًا أن الزيادة في وقت الحساب مع زيادة حجم المشكلة هي من الدرجة الثانية ، وزيادة أخرى

$N$ يجعل المهمة غير قابلة للحل في وقت معقول.

تنفيذ GPU

ولكن هناك رغبة في إجراء العمليات الحسابية بشكل أسرع. هناك العديد من الاتجاهات المتاحة للتسارع: حساب GPU ، تقريب الوظيفة

$f_n$ . أولاً ، بالنسبة لحوسبة GPU ، اخترت تقنية OpenCL. لمزيد من العمل المريح ، تم استخدام مكتبة CLHPP . تتمثل الميزة الرئيسية لـ OpenCL في أنه يمكن تشغيل التعليمات البرمجية على المعالج وعلى GPU ، مما يبسط عملية الكتابة والتصحيح ، بالإضافة إلى توسيع قائمة الأجهزة المراد تشغيلها. تساعد أداة Oclgrind في تصحيح الأخطاء ، والتي تظهر في وقت التشغيل مكالمات OpenCL API غير صحيحة ومشاكل الوصول إلى الذاكرة.

Opencl

للبدء في OpenCL ، تحتاج إلى الحصول على قائمة المنصات المتاحة. أكثر المنصات شيوعًا هي AMD و Intel و NVidia.

كود

 std::vector<cl::Platform> platforms; cl::Platform::get(&platforms);

بعد ذلك ، بعد اختيار النظام الأساسي ، تحتاج إلى تحديد جهاز الحوسبة الذي يمثله هذا النظام الأساسي:

كود

 const cl::Platform& platform(platforms[platform_n]); std::vector<cl::Device> all_devices; platform.getDevices(CL_DEVICE_TYPE_ALL, &all_devices);

وفي نهاية المرحلة التحضيرية ، من الضروري إنشاء سياق وقوائم انتظار يتم فيها تخصيص الذاكرة وسيتم إجراء العمليات الحسابية. على سبيل المثال ، يتم إنشاء سياق يجمع بين جميع أجهزة الحوسبة للنظام الأساسي المحدد على النحو التالي:

السياق وقانون إنشاء قائمة الانتظار

 cl::Context context(all_devices); std::vector<cl::CommandQueue> queues; for(cl::Device device: all_devices) queues.push_back(cl::CommandQueue(context, device));

لتنزيل الكود المصدري إلى جهاز حوسبة ، يجب تجميعه ، فئة cl :: Program مخصصة لهذا الغرض.

رمز تجميع Kernel

 std::vector< std::string > source_data; cl::Program::Sources sources; for(int i = 0; i != files.size(); ++i) { source_data.push_back(load_program(files[i]));//   sources.push_back(std::make_pair(source_data.back().data(), source_data.back().size())); } cl::Program prog(context, sources); devices.push_back(all_devices); prog.build(devices, options);

لوصف معلمات دالة (kernel) التي يتم تنفيذها على جهاز حوسبة ، يوجد قالب cl: make_kernel.

قوة التفاعل حساب نواة سبيل المثال

 typedef cl::make_kernel< cl_int, cl_int, //Block offset cl::Buffer, //mass cl::Buffer, //y cl::Buffer, //f cl_int, cl_int, //yoff,foff cl_int, cl_int //points_count,stride > ComputeBlock;

علاوة على ذلك ، كل شيء بسيط: نحن نعلن عن متغير مع نوع النواة ، وتمرير البرنامج المترجمة واسم النواة الحسابية فيه ، يمكننا أن نبدأ النواة مثل وظيفة عادية تقريبا.

كود إطلاق النواة

 ComputeBlock fcompute(prog, "ComputeBlockLocal"); cl::NDRange global_range(device_data_size); cl::NDRange local_range(block_size); cl::EnqueueArgs eargs(ctx.m_queue, global_range, local_range); fcompute(eargs, ...  ); //,   .

يشبه النواة الحسابية لـ OpenCL نفسها إلى حد كبير خيار "openmp + block + الأمثل" لوحدة المعالجة المركزية ، على عكس إصدار وحدة المعالجة المركزية فقط ، يتم التحكم في الدورة الأولى باستخدام OpenCL (يتم تحديد نطاق الدورة بواسطة المتغير global_range من رمز بدء تشغيل kernel ، ويتوفر رقم التكرار الحالي من kernel باستخدام الدالة get_global_id (0)). أولاً ، يتم تحميل جزء من بيانات النص من الذاكرة المحلية ، ثم معالجتها. تعتبر الذاكرة المحلية مشتركة بين جميع سلاسل الرسائل في المجموعة ، وبالتالي فإن التنزيل يحدث مرة واحدة للمجموعة ، ويتم معالجته بواسطة كل سلسلة رسائل في المجموعة ، وبما أن الذاكرة المحلية أسرع بكثير من العالمية ، والحسابات أسرع بكثير.

كود النواة

 __kernel void ComputeBlockLocal(int offset_n1, int offset_n2, __global const nbcoord_t* mass, __global const nbcoord_t* y, __global nbcoord_t* f, int yoff, int foff, int points_count, int stride) { int n1 = get_global_id(0) + offset_n1; __global const nbcoord_t* rx = y + yoff; __global const nbcoord_t* ry = rx + stride; __global const nbcoord_t* rz = rx + 2 * stride; __global const nbcoord_t* vx = rx + 3 * stride; __global const nbcoord_t* vy = rx + 4 * stride; __global const nbcoord_t* vz = rx + 5 * stride; __global nbcoord_t* frx = f + foff; __global nbcoord_t* fry = frx + stride; __global nbcoord_t* frz = frx + 2 * stride; __global nbcoord_t* fvx = frx + 3 * stride; __global nbcoord_t* fvy = frx + 4 * stride; __global nbcoord_t* fvz = frx + 5 * stride; nbcoord_t x1 = rx[n1]; nbcoord_t y1 = ry[n1]; nbcoord_t z1 = rz[n1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; __local nbcoord_t x2[NBODY_DATA_BLOCK_SIZE]; __local nbcoord_t y2[NBODY_DATA_BLOCK_SIZE]; __local nbcoord_t z2[NBODY_DATA_BLOCK_SIZE]; __local nbcoord_t m2[NBODY_DATA_BLOCK_SIZE]; // NB! get_local_size(0) == NBODY_DATA_BLOCK_SIZE for(int b2 = 0; b2 < points_count; b2 += NBODY_DATA_BLOCK_SIZE) { int n2 = b2 + offset_n2 + get_local_id(0); // Copy data block to local memory x2[ get_local_id(0) ] = rx[n2]; y2[ get_local_id(0) ] = ry[n2]; z2[ get_local_id(0) ] = rz[n2]; m2[ get_local_id(0) ] = mass[n2]; // Synchronize local work-items copy operations barrier(CLK_LOCAL_MEM_FENCE); nbcoord_t local_res_x = 0.0; nbcoord_t local_res_y = 0.0; nbcoord_t local_res_z = 0.0; for(int local_n2 = 0; local_n2 != NBODY_DATA_BLOCK_SIZE; ++local_n2) { nbcoord_t dx = x1 - x2[local_n2]; nbcoord_t dy = y1 - y2[local_n2]; nbcoord_t dz = z1 - z2[local_n2]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = (m2[local_n2]) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; local_res_x -= dx; local_res_y -= dy; local_res_z -= dz; } // Synchronize local work-items computations barrier(CLK_LOCAL_MEM_FENCE); res_x += local_res_x; res_y += local_res_y; res_z += local_res_z; } frx[n1] = vx[n1]; fry[n1] = vy[n1]; frz[n1] = vz[n1]; fvx[n1] = res_x; fvy[n1] = res_y; fvz[n1] = res_z; }

كودا

إن تطبيق نظام NVidia CUDA أبسط قليلاً من OpenCL ، فنحن لسنا بحاجة إلى إنشاء سياق الجهاز وإدارة قائمة انتظار التنفيذ بأنفسنا (على الأقل حتى نرغب في تنفيذ تطبيق متعدد GPU). كما في حالة OpenCL ، نحتاج إلى تخصيص ذاكرة على وحدة معالجة الرسومات ، ونسخ بياناتنا إليها ، ومن ثم يمكننا بدء تشغيل نواة الحوسبة.

يمكنك قراءة المزيد حول العمل مع CUDA هنا .

كود إطلاق نواة كودا

 dim3 grid(count / block_size); dim3 block(block_size); size_t shared_size(4 * sizeof(nbcoord_t) * block_size); kfcompute <<< grid, block, shared_size >>> (... ...);

على عكس OpenCL ، لا تحدد CUDA النطاق الكامل للتكرارات (في تطبيق OpenCL فهو global_range) ، ولكن تحدد حجم الشبكة وأحجام الكتلة في الشبكة ، وبالتالي ، يتغير حساب رقم النص الحالي بشكل طفيف ، وإلا فإن kernel يشبه OpenCL ، باستثناء الأسماء الأخرى وظائف التزامن و المحدد للذاكرة المشتركة. الميزة المميزة الأخرى المفيدة في CUDA هي أنه يمكننا تحديد الحجم المطلوب للذاكرة المشتركة عند بدء تشغيل kernel. كما هو الحال في تطبيق OpenCL ، في بداية كل كتلة تكرارية ، نقوم بنسخ جزء من البيانات إلى ذاكرة مشتركة ، ثم نعمل مع هذه الذاكرة من جميع مؤشرات ترابط الكتلة.

كود نواة كودا

 __global__ void kfcompute(int offset_n2, const nbcoord_t* y, int yoff, nbcoord_t* f, int foff, const nbcoord_t* mass, int points_count, int stride) { int n1 = blockDim.x * blockIdx.x + threadIdx.x; const nbcoord_t* rx = y + yoff; const nbcoord_t* ry = rx + stride; const nbcoord_t* rz = rx + 2 * stride; nbcoord_t x1 = rx[n1]; nbcoord_t y1 = ry[n1]; nbcoord_t z1 = rz[n1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; extern __shared__ nbcoord_t shared_xyzm_buf[]; nbcoord_t* x2 = shared_xyzm_buf; nbcoord_t* y2 = x2 + blockDim.x; nbcoord_t* z2 = y2 + blockDim.x; nbcoord_t* m2 = z2 + blockDim.x; for(int b2 = 0; b2 < points_count; b2 += blockDim.x) { int n2 = b2 + offset_n2 + threadIdx.x; // Copy data block to local memory x2[ threadIdx.x ] = rx[n2]; y2[ threadIdx.x ] = ry[n2]; z2[ threadIdx.x ] = rz[n2]; m2[ threadIdx.x ] = mass[n2]; // Synchronize local work-items copy operations __syncthreads(); nbcoord_t local_res_x = 0.0; nbcoord_t local_res_y = 0.0; nbcoord_t local_res_z = 0.0; for(int n2 = 0; n2 != blockDim.x; ++n2) { nbcoord_t dx = x1 - x2[n2]; nbcoord_t dy = y1 - y2[n2]; nbcoord_t dz = z1 - z2[n2]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = (m2[n2]) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; local_res_x -= dx; local_res_y -= dy; local_res_z -= dz; } // Synchronize local work-items computations __syncthreads(); res_x += local_res_x; res_y += local_res_y; res_z += local_res_z; } n1 += foff; f[n1 + 3 * stride] = res_x; f[n1 + 4 * stride] = res_y; f[n1 + 5 * stride] = res_z; }

جدول 3. تبعية وظيفة حساب الوقت (بالثواني)

$f_n$ على عدد من الهيئات المتفاعلة

$N$ لمختلف تطبيقات GPU وتطبيقات وحدة المعالجة المركزية أفضل

$N$	4096	8192	16384	32768	65536	131072
openmp + block + التحسين	0.0128	0.0495	0.194	0.774	---	---
OpenCL + نصف NVidia K80	0.004	0.008	0.026	0.134	0.322	1.18
CUDA + نصف NVidia K80	0.004	0.008	0.0245	0.115	0.291	1.13

أين يمكن الحصول على NVidia K80

تم إطلاق تطبيقات OpenCL و CUDA على خدمة Colab المجانية من Google ، والتي توفر الوصول إلى أجهزة كمبيوتر NVidia K80. يمكنك قراءة المزيد حول العمل مع هذه الخدمة على المحور

بشكل عام ، فإن النتيجة مخيبة للآمال ، أسرع فقط 5-6 مرات من تنفيذ وحدة المعالجة المركزية. حتى إذا أجرينا حسابات على K80 بالكامل ، فسنحصل على تسريع يصل إلى 12 مرة ، لكن منذ ذلك الحين نظرًا لأن تعقيد المشكلة من الدرجة الثانية ، فإنه في وقت معقول لا يمكننا معالجة 32768 من الهيئات المتفاعلة ، ولكن 131072 ، أي أكثر من 4 مرات فقط.

تقريب الوظيفة $f_n$

إذا نظرت عن كثب إلى الوظيفة ، التي تحددها القوة الجذابة لهذين الجسمين ، فمن الواضح أنه يتناقص من الناحية التربيعية مع المسافة. لذلك ، يمكننا حساب بدقة قوة التفاعل بين الهيئات القريبة ، وتقريبا بين تلك البعيدة. نهج واحد مشهور
هي خوارزمية ثلاثية الأبعاد اقترحها د. بارنز وب. هات. يتم بناء شجرة octree في الفضاء المحاكي ، تحتوي في أوراقها على إحداثيات وكتل الأجسام المحاكاة. تحتوي العقد الأصلية على مركز الكتلة والكتلة الكلية للعُقد الفرعية ونصف قطر المجال الموصوف حول أجسام العقد الفرعية. يحتوي جذر الشجرة على مركز كتلة جميع الأجسام وكتلتها الكلية ونصف قطر الكرة الموصوفة حولها. عند حساب قوة التفاعل ، يتم مراعاة المسافة إلى جذر الشجرة أولاً إذا كانت نسبة المسافة إلى العقدة إلى نصف قطرها أكبر من بعض الثابت

$\ lambda_ {crit}$ ثم يُعتبر الجذر هيئة واحدة ذات إحداثيات تساوي إحداثيات مركز كتلة الأجسام الموجودة فيه ، وكتلة تساوي مجموع كتل العقد البنت ، إذا كانت النسبة أقل من أو تساوي

$\ lambda_ {crit}$ ، ثم يتم تكرار الإجراء بشكل متكرر لكل عقدة تابعة. إذا تم الوصول إلى ورقة من شجرة ، ثم يتم النظر في قوة التفاعل بالطريقة المعتادة. وبالتالي ، إذا تم إزالة جسم واحد بعيدًا عن المجموعة المدمجة من الهيئات الأخرى ، يتم تقديم هذه المجموعة إليها كجسم واحد ، ويتم احتساب قوة التفاعل ليس على كل هيئة ، ولكن حتى هيئة واحدة فقط. بسبب هذا ، فإن تعقيد الخوارزمية يتناقص مع

$O (N ^ 2)$ قبل

$O (N \ log (N))$ على حساب بعض فقدان الدقة.

في طريقتي ، قررت عدم استخدام شجرة octree ، ولكن شجرة kd ، لأنه إنه سهل الاستخدام ويحتوي على مساحة تخزين أقل مقارنةً بأوكتري.

دعنا نعود إلى التنفيذ على وحدة المعالجة المركزية. يمكن تمثيل عقدة kd- شجرة في شكل فئة تحتوي على مؤشرات إلى أحفاد اليسار واليمين ومعلومات حول الإحداثيات والكتلة:

عقدة شجرة Kd

 class node { node* m_left; //!<   node* m_right; //!<   nbvertex_t m_mass_center; //!<     nbcoord_t m_mass; //!<   nbcoord_t m_radius_sqr; //!<    ,   lambda_crit nbvertex_t m_bmin; //!<     nbvertex_t m_bmax; //!<     size_t m_body_n; //!<  ,    };

من خلال طريقة تخزين الشجرة هذه ، لدينا خياران ممكنان لاجتياز الشجرة: إما استخدام التكرار الصريح ، أو استخدام المكدس بأنفسنا. أنا استقر على الخيار الثاني.

حساب قوة التفاعل من خلال اجتياز شجرة

 nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1) { nbvertex_t total_force; node* stack_data[MAX_STACK_SIZE] = {}; node** stack = stack_data; node** stack_head = stack; *stack++ = m_root; while(stack != stack_head) { node* curr = *--stack; const nbcoord_t distance_sqr((v1 - curr->m_mass_center).norm()); if(distance_sqr > curr->m_radius_sqr) {//  ,       total_force += force(v1, curr->m_mass_center, mass1, curr->m_mass); } else {//   ,      if(curr->m_right != NULL) { *stack++ = curr->m_right; } if(curr->m_left != NULL) { *stack++ = curr->m_left; } } } return total_force; }

كما في حالة تنفيذ وحدة المعالجة المركزية "الدقيقة" ، يتم استدعاء وظيفة حساب القوة لكل هيئة. يمكن موازاة الدورة عبر جميع الهيئات بسهولة باستخدام توجيهات OpenMP.

لكن تكرار الحلقات المجاورة في هذه الحالة سوف يشير إلى أجزاء مختلفة تمامًا من الشجرة ، والتي لا تسمح بالاستخدام الفعال لذاكرة التخزين المؤقت للمعالج. للتغلب على هذه المشكلة ، لا بد من اجتياز جميع الهيئات بالترتيب الأصلي ، ولكن بالترتيب الذي توجد به الجثث في أوراق شجرة kd ، ثم تحدث التكرارات المجاورة للأجسام القريبة من الفضاء ، وسوف تعبر الشجرة على طول نفس المسارات تقريبًا.

شجرة ورقة اجتياز

 template<class Visitor> void traverse(Visitor visit) { node* stack_data[MAX_STACK_SIZE] = {}; node** stack = stack_data; node** stack_head = stack; *stack++ = m_root; while(stack != stack_head) { node* curr = *--stack; if(curr->m_radius_sqr > 0) {//  .    . if(curr->m_left != NULL) { *stack++ = curr->m_left; } if(curr->m_right != NULL) { *stack++ = curr->m_right; } } else {//   .  . visit(curr->m_body_n, curr->m_mass_center, curr->m_mass); } } }

يحتوي هذا التنفيذ على مشكلة أخرى - لا توجد طريقة عالمية لموازنة مثل هذا اجتياز الأشجار. لكن يمكننا تغيير الطريقة التي يتم بها تخزين الشجرة في الذاكرة تمامًا - يمكننا تخزين جميع العقد في صفيف خطي واحد والتخلي تمامًا عن تخزين المؤشرات على المتحدرين ، وذلك عن طريق القياس مع بناء كومة ثنائية . عند بدء ترقيم العقد مع

$1$ إذا كانت العقدة في رقم الخلية

$i$ ، ثم طفله الأيسر في الزنزانة

$2i$ ، الطفل المناسب في الزنزانة

$2i + 1$ والأب في الخلية

$i / 2$ . العقدة اليمنى المقابلة لليسار مع الرقم

$i$ سوف يكون لها عدد

$i + 1$ . الصفيف نفسه سيكون لها طول

$2N$ ، وسيتم وضع جميع العقد ورقة في الماضي

$N$ الخلايا ، علاوة على ذلك ، سيتم وضع العقد متباعدة عن كثب في خلايا قريبة من مجموعة. ستتغير وظيفة اجتياز الشجرة قليلاً ، ولكن يبقى إطار العمل كما هو:

حساب القوة من خلال اجتياز شجرة في مجموعة

 nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1) { nbvertex_t total_force; size_t stack_data[MAX_STACK_SIZE] = {}; size_t* stack = stack_data; size_t* stack_head = stack; *stack++ = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { size_t curr = *--stack; const nbcoord_t distance_sqr((v1 - m_mass_center[curr]).norm()); if(distance_sqr > m_radius_sqr[curr]) { total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]); } else { size_t left(left_idx(curr)); size_t rght(rght_idx(curr)); if(rght < m_body_n.size()) { *stack++ = rght; } if(left < m_body_n.size()) { *stack++ = left; } } } return total_force; }

ولكن هذا ليس كل الاحتمالات التي يفتحها لنا تخزين العقد في الصفيف - يمكننا رفض المكدس عند الزحف. للقيام بذلك ، في فرع الشفرة الذي نذهب فيه إلى أطفال العقدة ، نضيف الوظيفة لحساب العقدة التالية (

$next_ {up}$ ) ، وفي الفرع الذي نحسب فيه قوة التفاعل ، نضيف حساب العقدة التالية مع تخطي الشجرة الفرعية الحالية (

$skip_ {down}$ )

لتخطي الشجرة الفرعية الحالية ، نحتاج إلى الانتقال إلى الجذر (الاتجاه

$D$ ) ، بينما نحن في المنحدر الأيمن ، حالما نصل إلى اليسار ، نذهب إلى الشجرة اليمنى المقابلة (الاتجاه

$R$ ) ، إذا وصلنا إلى الجذر ، ثم اكتمال اجتياز شجرة.

الشجرة الفرعية تخطي رمز الوظيفة

 index_t skip_down(index_t idx) { // While index is 'right' -> go down while(is_right(idx)) { index_t parent = parent_idx(idx); // We at root again. Stop traverse. if(parent == NBODY_HEAP_ROOT_INDEX) { return NBODY_HEAP_ROOT_INDEX; } idx = parent; } return left2right(idx); }

الشكل 8. تخطي الشجرة الفرعية

$skip_ {down}$ .

للانتقال إلى العقدة التالية ، إن أمكن ، انتقل إلى الطفل الأيسر (الاتجاه

$يو$ ) ، وإذا لم يكن هناك سليل ، فانتقل إلى العقدة التالية "من الأسفل" باستخدام الوظيفة

$skip_ {down}$ .

انتقل إلى رمز وظيفة العقدة التالية

 index_t next_up(index_t idx, index_t tree_size) { index_t left = left_idx(idx); if(left < tree_size) { return left; } return skip_down(idx); }

الشكل 9. الانتقال إلى العقدة التالية

$next_ {up}$ .

قد يبدو أننا استبدلنا العودية بحلقة

$بينما$ في الوظيفة

$skip_ {down}$ ، ومثل هذا الاستبدال لا يعطي أي شيء ، ولكن دعونا نرى كيفية تحديد ما إذا كانت العقدة برقم

$i$ السليل الصحيح. يمكن القيام بذلك ببساطة عن طريق التحقق من رقمه الفردي (الطفل المناسب في الخلية

$2i + 1$ ) ، لهذا يكفي لحساب

$i \ & 1$ . أي نقسم الرقم

$i$ اثنين إذا تم تعيين بت الأقل أهمية إلى واحد. ولكن يمكن القيام بذلك بدون حلقة ، في العديد من المعالجات ، هناك إرشادات العثور على المجموعة الأولى تقوم بإرجاع موضع بت المجموعة الأولى ، نستخدمها لتحويل الحلقة إلى أربعة تعليمات للمعالج.

محسن تخطي رمز الشجرة وظيفة

 index_t skip_down(index_t idx) { idx = idx >> (__builtin_ffs(~idx) - 1); return left2right(idx); }

بعد ذلك ، يمكننا استبعاد المكدس من وظيفة اجتياز الشجرة واستبدالها بزوج

$skip_ {down} + next_ {up}$ ، بعد ذلك تبدو الوظيفة أكثر بساطة:

فرض الحساب عن طريق اجتياز شجرة في صفيف دون استخدام مكدس

 nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1) const { nbvertex_t total_force; size_t curr = NBODY_HEAP_ROOT_INDEX; size_t tree_size = m_mass_center.size(); do { const nbcoord_t distance_sqr((v1 - m_mass_center[curr]).norm()); if(distance_sqr > m_radius_sqr[curr]) { total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]); curr = skip_down(curr); } else { curr = next_up(curr, tree_size); } } while(curr != NBODY_HEAP_ROOT_INDEX); return total_force; }

في المجموع ، حصلنا على ستة مجموعات من اجتياز الأشجار وحساب القوة. قارن هذه الطرق من حيث وقت الحساب والجودة. نأخذ كمقياس للجودة التغير النسبي في إجمالي طاقة النظام بعد 100 تكرار. كنظام نموذجي ، نأخذ اثنين من "المجرات" المتفاعلة تتكون من

$16384$ .

4.

/		''	''
	cycle+tree	cycle+heap	cycle+heapstackless
	nestedtree+tree	nestedtree+heap	nestedtree+heapstackless


a) $f_n$ ( $\lambda_{crit}$ ).	b) ( $\lambda_{crit}$ ).
10. $f_n$ CPU ( $N=32768$ )

, 'nestedtree+tree' , .. . .

$\lambda_{crit} > 1$ . . 10a , (

$\lambda_{crit} < 10$ )

$f_n$ ('openmp+block+optimization'),

$\lambda_{crit}$ .

GPU

GPU OpenCL, CUDA. , . , CPU .

OpenCL ( )

 __kernel void ComputeTreeBH(int offset_n1, int points_count, int tree_size, __global const nbcoord_t* y, __global nbcoord_t* f, __global const nbcoord_t* tree_cmx, __global const nbcoord_t* tree_cmy, __global const nbcoord_t* tree_cmz, __global const nbcoord_t* tree_mass, __global const nbcoord_t* tree_crit_r2) { int n1 = get_global_id(0) + offset_n1; int stride = points_count; __global const nbcoord_t* rx = y; __global const nbcoord_t* ry = rx + stride; __global const nbcoord_t* rz = rx + 2 * stride; __global const nbcoord_t* vx = rx + 3 * stride; __global const nbcoord_t* vy = rx + 4 * stride; __global const nbcoord_t* vz = rx + 5 * stride; __global nbcoord_t* frx = f; __global nbcoord_t* fry = frx + stride; __global nbcoord_t* frz = frx + 2 * stride; __global nbcoord_t* fvx = frx + 3 * stride; __global nbcoord_t* fvy = frx + 4 * stride; __global nbcoord_t* fvz = frx + 5 * stride; nbcoord_t x1 = rx[n1]; nbcoord_t y1 = ry[n1]; nbcoord_t z1 = rz[n1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int stack_data[MAX_STACK_SIZE] = {}; int stack = 0; int stack_head = stack; stack_data[stack++] = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { int curr = stack_data[--stack]; nbcoord_t dx = x1 - tree_cmx[curr]; nbcoord_t dy = y1 - tree_cmy[curr]; nbcoord_t dz = z1 - tree_cmz[curr]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > tree_crit_r2[curr]) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tree_mass[curr] / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; } else { int left = left_idx(curr); int rght = rght_idx(curr); if(left < tree_size) { stack_data[stack++] = left; } if(rght < tree_size) { stack_data[stack++] = rght; } } } frx[n1] = vx[n1]; fry[n1] = vy[n1]; frz[n1] = vz[n1]; fvx[n1] = res_x; fvy[n1] = res_y; fvz[n1] = res_z; }

, , GPU. , , , .. . , , , , , , tn1.

OpenCL ( )

 __kernel void ComputeHeapBH(int offset_n1, int points_count, int tree_size, __global const nbcoord_t* y, __global nbcoord_t* f, __global const nbcoord_t* tree_cmx, __global const nbcoord_t* tree_cmy, __global const nbcoord_t* tree_cmz, __global const nbcoord_t* tree_mass, __global const nbcoord_t* tree_crit_r2, __global const int* body_n) { int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX; int stride = points_count; int tn1 = get_global_id(0) + offset_n1 + tree_offset; int n1 = body_n[tn1]; nbcoord_t x1 = tree_cmx[tn1]; nbcoord_t y1 = tree_cmy[tn1]; nbcoord_t z1 = tree_cmz[tn1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int stack_data[MAX_STACK_SIZE] = {}; int stack = 0; int stack_head = stack; stack_data[stack++] = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { int curr = stack_data[--stack]; nbcoord_t dx = x1 - tree_cmx[curr]; nbcoord_t dy = y1 - tree_cmy[curr]; nbcoord_t dz = z1 - tree_cmz[curr]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > tree_crit_r2[curr]) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tree_mass[curr] / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; } else { int left = left_idx(curr); int rght = rght_idx(curr); if(left < tree_size) { stack_data[stack++] = left; } if(rght < tree_size) { stack_data[stack++] = rght; } } } __global const nbcoord_t* vx = y + 3 * stride; __global const nbcoord_t* vy = y + 4 * stride; __global const nbcoord_t* vz = y + 5 * stride; __global nbcoord_t* frx = f; __global nbcoord_t* fry = frx + stride; __global nbcoord_t* frz = frx + 2 * stride; __global nbcoord_t* fvx = frx + 3 * stride; __global nbcoord_t* fvy = frx + 4 * stride; __global nbcoord_t* fvz = frx + 5 * stride; frx[n1] = vx[n1]; fry[n1] = vy[n1]; frz[n1] = vz[n1]; fvx[n1] = res_x; fvy[n1] = res_y; fvz[n1] = res_z; }

. . , , , .. , . , , , , , , . , , . أي , . . . ( ). CUDA __hiloint2double , .

 template<> struct nb1Dfetch<double> { typedef double4 vec4; static __device__ double fetch(cudaTextureObject_t tex, int i) { int2 p(tex1Dfetch<int2>(tex, i)); return __hiloint2double(py, px); } static __device__ vec4 fetch4(cudaTextureObject_t tex, int i) { int ii(2 * i); int4 p1(tex1Dfetch<int4>(tex, ii)); int4 p2(tex1Dfetch<int4>(tex, ii + 1)); vec4 d4 = {__hiloint2double(p1.y, p1.x), __hiloint2double(p1.w, p1.z), __hiloint2double(p2.y, p2.x), __hiloint2double(p2.w, p2.z) }; return d4; } };

, (x, y, z, tree_crit_r2) , . , r2 > tree_crit_r2[curr] , . CUDA L1 ( cudaFuncSetCacheConfig ). , L1 .

CUDA ( )

 __global__ void kfcompute_heap_bh_tex(int offset_n1, int points_count, int tree_size, nbcoord_t* f, cudaTextureObject_t tree_xyzr, cudaTextureObject_t tree_mass, const int* body_n) { nb1Dfetch<nbcoord_t> tex; int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX; int stride = points_count; int tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset; int n1 = body_n[tn1]; nbvec4_t xyzr = tex.fetch4(tree_xyzr, tn1); nbcoord_t x1 = xyzr.x; nbcoord_t y1 = xyzr.y; nbcoord_t z1 = xyzr.z; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int stack_data[MAX_STACK_SIZE] = {}; int stack = 0; int stack_head = stack; stack_data[stack++] = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { int curr = stack_data[--stack]; nbvec4_t xyzr2 = tex.fetch4(tree_xyzr, curr); nbcoord_t dx = x1 - xyzr2.x; nbcoord_t dy = y1 - xyzr2.y; nbcoord_t dz = z1 - xyzr2.z; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > xyzr2.w) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tex.fetch(tree_mass, curr) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; } else { int left = nbody_heap_func<int>::left_idx(curr); int rght = nbody_heap_func<int>::rght_idx(curr); if(left < tree_size) { stack_data[stack++] = left; } if(rght < tree_size) { stack_data[stack++] = rght; } } } f[n1 + 3 * stride] = res_x; f[n1 + 4 * stride] = res_y; f[n1 + 5 * stride] = res_z; }

nvprof , .

, CUDA , '' , , , , '' , , .

, , . , , , .

CUDA

 __global__ void kfcompute_heap_bh_stackless(int offset_n1, int points_count, int tree_size, nbcoord_t* f, cudaTextureObject_t tree_xyzr, cudaTextureObject_t tree_mass, const int* body_n) { nb1Dfetch<nbcoord_t> tex; int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX; int stride = points_count; int tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset; int n1 = body_n[tn1]; nbvec4_t xyzr = tex.fetch4(tree_xyzr, tn1); nbcoord_t x1 = xyzr.x; nbcoord_t y1 = xyzr.y; nbcoord_t z1 = xyzr.z; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int curr = NBODY_HEAP_ROOT_INDEX; do { nbvec4_t xyzr2 = tex.fetch4(tree_xyzr, curr); nbcoord_t dx = x1 - xyzr2.x; nbcoord_t dy = y1 - xyzr2.y; nbcoord_t dz = z1 - xyzr2.z; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > xyzr2.w) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tex.fetch(tree_mass, curr) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; curr = nbody_heap_func<int>::skip_idx(curr); } else { curr = nbody_heap_func<int>::next_up(curr, tree_size); } } while(curr != NBODY_HEAP_ROOT_INDEX); f[n1 + 3 * stride] = res_x; f[n1 + 4 * stride] = res_y; f[n1 + 5 * stride] = res_z; }

, GPU, , . , , . , , , , . . NVidia K80.

5. ( )

$f_n$ GPU

$N=131072$

$\lambda_{crit}=10$

/	8	16	32	64	128	256	512	1024
opencl+dense	5.77	2.84	1.46	1.13	1.15	1.14	1.14	1.13
cuda+dense	5.44	2.55	1.27	0.96	0.97	0.99	0.99	-
opencl+heap+cycle	5.88	5.65	5.74	5.96	5.37	5.38	5.35	5.38
opencl+heap+nested	4.54	3.68	3.98	5.25	5.46	5.41	5.48	5.31
cuda+heap+nested	3.62	2.81	2.68	4.26	4.84	4.75	4.8	4.67
cuda+heap+nested+tex	2.6	1.51	0.912	0.7	1.85	1.75	1.69	1.61
cuda+heap+nested+tex+stackless	2.3	1.29	0.773	0.5	0.51	0.52	0.52	0.52

6. ( )

$f_n$ GPU

$N=1M$

$\lambda_{crit}=4$

/	8	16	32	64	128	256	512	1024
opencl+dense	366	179	89.9	69.3	70.3	69.1	68.9	68.0
cuda+dense	346	162	79.6	60.8	60.8	60.7	59.6	-
opencl+heap+cycle	16.2	18.2	20.1	21.2	21.2	21.3	21.2	21.1
opencl+heap+nested	10.5	7.63	6.38	8.23	9.95	9.89	9.65	9.66
cuda+heap+nested	8.67	6.44	5.39	5.93	8.65	8.61	8.41	8.27
cuda+heap+nested+tex	6.38	3.57	2.13	1.44	3.56	3.46	3.30	3.29
cuda+heap+nested+tex+stackless	5.78	3.19	1.83	1.21	1.11	1.10	1.11	1.13

, , , CPU , , . 'opencl+heap+cycle' 6

$f_n$ . 'opencl+heap+nested', , 1.4 , .. . 'cuda+heap+nested' L1 , 1.4 , , cuda ( 'opencl+dense' 'cuda+dense' , cuda ~1.2 ). ( 3.8 ) . 'cuda+heap+nested+tex+stackless' 1.4 , .. . ,

$\lambda_{crit}=10$

$f_n$ . لكن

$\lambda_{crit}=10$ , CPU ,

$\lambda_{crit}$ .

$\lambda_{crit}$ , .


a) $N=128K$	b) $N=1M$
11. $f_n$ ( $\lambda_{crit}$ ) GPU

$\lambda_{crit}$

$f_n$ , kd- GPU. ,

$\lambda_{crit}\leq 4$ , . ,

$N=128K$

$\lambda_{crit}=1024$ , , GPU , L1 'branch divergence' . , (cuda+heap+nested+tex+stackless),

$1.4-1.5$ . . GPU .

GeForce GTX 1080 Ti ( )

7. ( )

$f_n$ GPU

$N=1M$

$\lambda_{crit}=4$

/	8	16	32	64	128	256	512	1024
opencl+dense	47.8	23.4	11.6	11.59	12.8	12.8	12.8	12.8
cuda+dense	49.0	23.8	11.9	11.8	11.7	11.7	11.7	11.7
opencl+heap+cycle	7.48	8.26	7.73	7.36	7.33	7.27	7.25	7.26
opencl+heap+nested	1.33	1.20	1.41	2.46	2.53	2.49	2.44	2.47
cuda+heap+nested	1.23	1.10	1.31	2.28	2.29	2.28	2.23	2.25
cuda+heap+nested+tex	0.88	0.68	0.654	1.6	1.6	1.6	1.6	1.6
cuda+heap+nested+tex+stackless	0.71	0.47	0.45	0.43	0.43	0.42	0.41	0.395

12.

$f_n$ (

$\lambda_{crit}$ ) GPU

GeForce GTX 1080 Ti , , , . , GPU . 5-7 , GPU, , , . , .

, — (

$2^{20}$ ) , GPU. GPU (Tesla V100), , , .. , Tesla K80. , , , , , .

الخاتمة

, . , « »,

$N$ , , .

التصور

, .

. 60 .

, . 99% . . . . — , — , — . , , , .

'' , . 10% . . '' , , .

5% '' .

10- .

.

مهمة N الهيئات أو كيفية تفجير مجرة ​​دون مغادرة المطبخ

فيزياء الظاهرة

الرياضيات

ملخص

تنفيذ وحدة المعالجة المركزية

تنفيذ GPU

Opencl

كودا

تقريب الوظيفة fn f_n

GPU

الخاتمة

التصور

More articles:

مهمة N الهيئات أو كيفية تفجير مجرة دون مغادرة المطبخ

تقريب الوظيفة $f_n$