عند اللعب وفقًا لقواعد Gomoku القياسية ، لا يحتاج Black إلى أكثر من
35 خطوة للفوز. يقدم المقال انتباهكم إلى استراتيجية الفوز كاملة والخوارزمية المقابلة للعبة.
عرض توضيحي للحل الكامل -
هنا - يمكنك اللعب وإيجاد أطول الخيارات. يفوز البرنامج وينفق عليه دائمًا ما لا يزيد عن 35 خطوة. شفرة المصدر للتطبيق ، والحل نفسه وأمثلة من الأطراف في نهاية المقال.
لن أتطرق إلى قواعد اللعبة وتكتيكاتها. تمت مناقشة الموضوع بالتفصيل على habr
هنا ، وكذلك خوارزميات القرار
هنا وهنا .
استطراد صغير
قبل عصر الهواتف الذكية ، كان التشنج اللاإرادي "خمسة على التوالي" (جوموكو ، رينجو) أحد أكثر القتلة شهرة في دروس المدرسة. كان النظر إلى المجموعات أكثر إثارة للاهتمام من تطور الاقتصاد الوطني لشمال إفريقيا أو تصنيف زهور البرسيم.
في خريف عام 1985 ، تم أخذ الفتيات من الصف العاشر لدينا من فصل الرياضيات. نحن ، الأطفال الستة الباقون ، كانوا على الأرجح على اتصال غير رسمي مع مدرس رياضيات حول الموضوعات المجردة. دخل المعلم الفصل في صمت ، وسلّم منشورات إلى كل شخص في صندوق وبدأ في كتابة أسماء الحاضرين على السبورة. لقد كنا مكتئبين ، تم التخطيط للعمل المستقل أو إجراء مسح. لكن القائمة الموجودة على السبورة تحولت إلى ترتيب وتم إعلان قواعد البطولة. كل مع كل سلسلة من خمسة أحزاب. جائزة للفائز - خمسة للمجلة. وفقًا لنتائج البطولة ، كنت محظوظًا بالفوز ، لكن اللعبة لم تنته هناك. وعد المعلم بوضع الأطفال الخمسة جميعهم إذا فاز الفائز في جميع مباريات السلسلة الخمسة على التوالي. يتم إعطاء حق الخطوة الأولى للفائز. على عكس تأكيد معلمنا أنه في مثل هذه الحالة ، مع اللعبة المناسبة ، يمكنك الفوز بـ 10 أو 100 أو أي عدد من الألعاب على التوالي ، بدا النصر لي محظوظًا للغاية.
بعد تسع سنوات ، في عام 1994 ، ذكر الدكتور لويس فيكتور أليس دليلًا على هذه الفرضية في مقال لـ
Go-Moku و Threat-Space Search . لم ينشر المؤلف إستراتيجيته الفائزة ، والتي تسمح له بالتحقق من الدليل. ومع ذلك ، في كتابه عام 1996 "
البحث عن حلول في الألعاب والذكاء الاصطناعي" ، تم تقديم وصف عام للخوارزميات. في الختام ، نذكر بشكل منفصل إجراء التحقق من اكتمال استراتيجية الفوز ، والتي تعتمد على صحة تنفيذ خوارزمية البحث عن "تسلسل التهديدات" وتحليل خيارات الخصم المضاد.
توضح أمثلة الحلول المقدمة في المقالة والكتاب مع "التحركات الصحيحة" للمعارضين ، والتي تعد جزءًا من استراتيجية رابحة ، ضعف الخوارزمية المستخدمة.

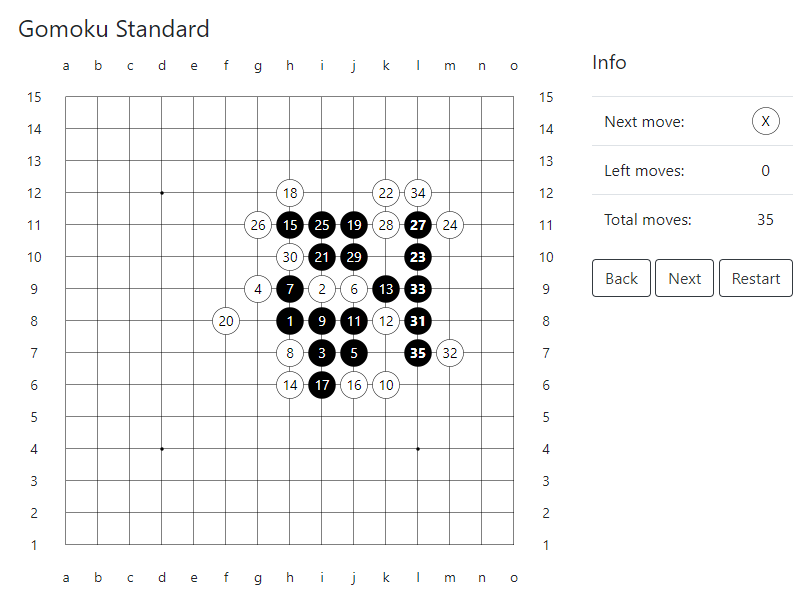
على سبيل المثال ، في الشكل ، حل البرنامج لقواعد جوموكو القياسية. إذا قام Black بالرد على j10 ثم j8 استجابةً لخطوة White's العاشرة g9 ، فستنتهي اللعبة بـ 29 حركة بدلاً من 45. ثم البرنامج "لم يلاحظ" مزيج "تسلسل التهديدات" من Black في 17 خطوة بعد الـ16 وبعد 26- تحرك الأبيض. وفي النهاية ، إذا قام وايت بعمل الخطوة السادسة والثلاثين (f12) بدلاً من j12 ، فسيتمسك به على الأقل حتى الخطوة 49. في الإنصاف ، يجب أن يقال أنه في هذا المثال ، لا تترك كل تحركات Black لأي أبيض أي فرصة لإنهاء اللعبة لصالحه.
على شبكة الإنترنت ، وجدت العديد من الإشارات إلى عمل مماثل يبحث عن استراتيجية فائزة. لا تزال مسألة تحسين الحلول الموجودة دون حل. ما هو الحد الأدنى لعدد التحركات التي يحتاجها الأسود للفوز؟
لذلك ، بعد قضاء وقت فراغ بسيط ، وموارد حوسبة حديثة ، وإشادة بهوايات الأطفال بعد 33 عامًا من بطولة المدرسة التي لا تنسى ، حدد مهمة العثور على الإستراتيجية المثلى للفوز بـ Black in Gomoku.
رقمنة الموقف على السبورة
تسجيل جزء بدائي جدا. لا يوجد سوى 225 خلية في هذا المجال. وفقًا لذلك ، يتم ترميز كل خلية بمقدار 1 بايت. لتسجيل دفعة من 35 حركة ، فقط 35 بايت مطلوبة. لكن مثل هذا السجل غير مناسب لتقييم الموقف لسببين: يمكن الحصول على نفس الموقف في تسلسل مختلف من التحركات ولا تؤخذ المواقف المتماثلة في الاعتبار.
يمكن تحقيق هدف اللعبة - بناء خمسة أحجار على التوالي - في واحد من أربعة اتجاهات: رأسية وأفقية واثنين من الأقطار. وبالتالي ، يمكننا تمثيل أي موقف كمجموعة من الخطوط. خطوط أفقية ورأسية بطول 15 خلية وخطوط قطرية بطول من 1 إلى 15 خلية. كل خطوة تغير قيمة 4 خطوط في اتجاهات مختلفة في وقت واحد.
مهمة تقييم الموقف هي تحديد جميع الأرقام المهمة لكل سطر. للبساطة ، نحن تصف كل خلية من الخط مع 2 بت. البتة الأولى ممتلئة عندما يتم تثبيت الحجر الأبيض ، والبت الثاني هو الحجر الأسود. لا يحتوي كل سطر على أكثر من 15 خلية ويتم ترميزه في عدد صحيح 32 بت. وبالتالي ، يتم تقليل البحث عن الأشكال على خط لمقارنة القيمة العددية للخط من خلال نافذة منزلقة مع نمط بت الشكل.

في المثال الموضح في الشكل ، يتم وصف الموضع بـ 26 سطرًا. وفقًا لذلك ، يتم ترميزه باستخدام 104 بايت ، بينما لا يتطلب سجل الدُفعات العادية سوى 17 بايت.
من السهل تخمين أنه يتم الحصول على جميع التماثلات - المنعطفات والصور المتطابقة - ببساطة عن طريق تغيير الرقم (خلط) واتجاه الخطوط. لتحديد موضع والبحث السريع للمجموعات ، يطبق هذا المبدأ وظيفة تجزئة 32 بت تعطي قيمًا مختلفة فقط للمواضع غير المتماثلة.
استخدام التماثلات يقلل بشكل كبير من عدد المواقف التي تم النظر فيها. على سبيل المثال ، يتم تقليل عدد خيارات الحركة الثانية من 224 إلى 35.
عند البحث عن حلول ومجموعات (سيتم مناقشتها أدناه) ، فإن المواضع المحسوبة تشكل رؤوس الرسم البياني متعدد الطبقات. يتم تجميع القمم في طبقات وفقًا لعدد الخلايا المملوءة. تشكل الحركات حواف الرسم البياني ، وتربط رؤوس الطبقات المجاورة. عندما يتم تجاهل التحركات غير الناجحة أثناء البحث ، يتم حذف الحواف وتفقد بعض الرؤوس اتصالها بالفرع الرئيسي. لذلك ، بعد خطوات الحساب ، يتم تنفيذ تجميع البيانات المهملة (أو إعادة إنشاء الرسم البياني من الأعلى).
أثناء عملية التطوير ، تم أخذ عدة خوارزميات تشفير بعين الاعتبار ، لكن الخوارق الموضحة أعلاه أظهرت أعلى معدل لتقدير الموقع.
تقييم الموقف
أحد العوامل المهمة لتقييم الموقف هو مدى أهمية قيام المعارضين ببناء الأجزاء المهمة.
خمسة - إذا تم العثور على هذه القطعة على السبورة ، فإن اللعبة قد انتهت. للقواعد القياسية ، لا تمنح الستات والسبعات وما إلى ذلك جائزة جوموكو. لذلك ، فإن الخمسة ، بالمناسبة ، جميع الشخصيات الأخرى ، تتطلب عدم وجود أحجارهم على الخلايا المجاورة في خط.
 الأربعة المفتوحة
الأربعة المفتوحة - بطول 6 خلايا ، الأربعة الوسطى مشغولة بالحجارة من نفس اللون ، الخارجي منها فارغ بالضرورة. حسنًا ، كما هو الحال بالنسبة لخمسة أشخاص ، فإن أحجارهم غائبة في الخلايا المجاورة. شخصية قوية للغاية تعني الفوز حتى عند تحرك شخص آخر.
 أربعة
أربعة - طول 5 خلايا ، واحدة (أي) من الخلايا الخمس مجانية. يعطي الفوز من تلقاء نفسه. إنه يخلق تهديدًا ويجبر الخصم على التحرك في خلية حرة إذا لم يكن لديه الأربعة. يعطي 5 نقاط في تصنيف الموقف أثناء الدفاع.

 ثلاثية مفتوحة
ثلاثية مفتوحة - طول 6 أو 7 خلايا ، الخلايا البعيدة هي حرة بالضرورة. بالنسبة لـ 6 خلايا ، فإن ثلاثة من الخلايا الأربعة المتوسطة تشغلها أحجار من نفس اللون ، واحدة خالية. لمدة 7 خلايا - ثلاث منها متوسطة تشغلها الحجارة من نفس اللون. تصبح القطعة بدورها أربعة مفتوحة إذا لم يكن لدى الخصم أربعة أو ثلاثة مفتوحة. على خطوة شخص آخر ، فإنه يخلق تهديدا ويجبر الخصم على إغلاق الثلاثة أو وضع الأربعة في الرد. تحتوي الخلية السادسة ثلاثية على حركة رفع و 3 حركات إغلاق. تحتوي الخلية السابعة ثلاثية على حركات رفع وخطوتين إغلاق فقط. يعطي 2-4 نقاط في تصنيف الموقف.


 الثلاثي
الثلاثي ، أو الثلاثي المغلق ، يبلغ طوله 5 خلايا ، أي ثلاثة منها مشغولة بالحجارة من نفس اللون. يمكن تحويل الثلاثة في دورهم إلى أربعة ويستخدم في الهجوم والدفاع ، مما يخلق تهديدًا أكثر من ثلاثة من الخصم. يعطي 1 نقطة في تصنيف الموقف.


 فتح
فتح (منظور)
شيطان - من 6 إلى 7 خلايا طويلة. عند الهجوم ، يتم تحويله إلى ثلاثة مفتوحة. يعطي 1 أو 2 نقطة في تصنيف الموقف.


 السدادة
السدادة هي في الوقت نفسه تهديدان أو أكثر لا يمكن إغلاقهما دفعة واحدة. هناك 3x3 شوكات (ثلاثية ثلاثية) ، 3x4 (ثلاثيات مفتوحة و أربع) و شوكات 4x4 (أربعين مفتوحتين). تقدم الشوكات فوزًا إذا لم يكن لدى الخصم تهديد أكبر - أربعة أو ثلاثة مفتوحين لشوكة 3x3 ، أو لا يمكن للخصم إغلاق الشوكة بشكل متتابع ، خلق تهديدات كبيرة - سلسلة من أربع لشوكة 3x3.



 الجمع
الجمع - تسلسل مستمر للتهديدات والدفاعات ضد تهديدات الخصم الأكثر أهمية ، مما يؤدي إلى نتيجة إيجابية للاعب. المجموعات تهاجم (أو تفوز) ودفاعية.
تركيبة المهاجمة أو الرابحة ناجحة إذا تم العثور على حركات استجابة تؤدي إلى الفوز على أي تحركات دفاعية أو هجومية. وينتهي مزيج الهجوم بتركيب سدادة لا يمكن للخصم إغلاقها.
التوليفة الدفاعية ، على العكس ، تنجح عندما يتوقف الخصم عن إنشاء تهديدات ، أو يتم تجاوز حد التحركات الحسابية. مزيج دفاعي يتكون من حركات دفاعية أو خلق تهديد أكبر للخصم.
عند تقييم المركز ، يتم إجراء بحث عن مجموعة فائزة. إذا نجحت ، فزنا. خلاف ذلك ، إذا لم تكن هناك تهديدات من الخصم ، تكون الدولة محايدة. إذا كانت هناك تهديدات من الخصم ، فإننا نبحث عن مزيج دفاعي. إذا نجحت ، فإن الدولة محايدة ؛ وإذا فشلت ، فسوف نخسر.
نظرًا لأن عدد خيارات المهاجمة والتحركات القسرية الانتقامية محدود جدًا ، يجوز البحث عن مجموعات ذات عمق كبير بدرجة كافية. أثناء الإنشاء الأولي للاستراتيجية المثلى ، تم تأسيس العمق المسموح به للبحث عن المجموعات على 25 حركة. عند إعادة حساب الحل لتطبيق خوارزمية تقدير الموقع في javascript ، تم تقليل عمق البحث المسموح به إلى 17 حركة.
عند حساب الإستراتيجية المثلى ، كان عمق البحث للمجموعة الفائزة من الأعلى محدودًا بالإضافة إلى الحد الأقصى المستهدف لعدد الحركات.
نحن نبحث عن حل
لذلك ، قمنا بتصنيف الموضع المحدد بأنه محايد واختر ما ستكون عليه الخطوة التالية. يعتمد سلوكنا في هذه الحالة على ما إذا كنا الجانب المهاجم أو المدافع. بالنسبة للجانب المهاجم ، سيكون الحل الكامل هو سلسلة من الحركات التي يتم من خلالها تقييم الموضع على أنه الفائز (أي مجموعة رابحة) بالنسبة لحركة أي خصم ، أو أنه يحتوي على الخطوة التالية في الحل. تجدر الإشارة إلى أنه لحساب الاستراتيجية المثلى ، يكون الجانب المهاجم أسودًا دائمًا ، والجانب المدافع أبيض.
يحتاج الجانب المهاجم إلى العثور على خطوة واحدة فقط ، مما يؤدي إلى أسرع انتصار. في ظروف نقص الموارد ، يحد المهاجم بشكل مصطنع من عدد خيارات الانتهاك ، سأبحث أولاً في الحركات المؤدية إلى الموضع بأعلى درجة تقييم. بعد العثور على أي حلول ، في اتجاه أطولها ، يوسع المهاجم نطاق الخيارات ، ويستكشف مواقع أقل تصنيفًا من أجل تقليل طول الحل.
يكفي أن يجد الجانب المدافع خطوة واحدة لا تؤدي إلى انتصار الخصم في الحد المحدد للحركات. يمكن استخدام جميع الخلايا الحرة للتعداد.
لتقليل عدد الحركات المراد فرزها ، نستخدم خوارزمية "تخطي". نحن نتخطى هذه الخطوة الدفاعية ونبحث عن تشكيلة هجومية رابحة. إذا نجحت ، قد تقتصر التحركات الدفاعية المحتملة على التحركات التي تؤثر على نجاح المجموعة المختلطة. في المتوسط ، يسمح لك هذا في كل خطوة بتقليل مساحة البحث بمقدار 4-6 مرات. يرجى ملاحظة أنه من بين التحركات التي تم تجاهلها ، قد يكون هناك فروع أطول للحل. لذلك ، للبحث عن الحلول المثلى ، يتم استخدام خوارزمية "تخطي" فقط في البحث الأولي.
نحسب الاستراتيجية
جميع المكونات جاهزة ، وضعنا أول حجر أسود في وسط الملعب ، وابدأ البحث عن حل ... وفي هذا ، بعد بضع ساعات ، نفدت موارد جهاز الكمبيوتر المحمول وعلي أن أعترف بالهزيمة "في المعركة ، ولكن ليس في المعركة".
في الواقع ، كان لدي في متناول يدي قوة الحوسبة مع مائة ونصف النوى زيون وتيرابايت من ذاكرة الوصول العشوائي الحرة. ولكن ، تذكر أنه في منتصف التسعينات ، كان لدى Allis 10 SUN SPARCstation 2 فقط على كل من 128 ميغابايت من ذاكرة الوصول العشوائي ، وشعر بالندم على السلوك غير الرياضي وقررت قصر مقدار ذاكرة الوصول العشوائي على جهاز java على 1 غيغابايت وخصصت خيطًا واحدًا فقط للمهمة المعالج. يمكن أن تعوض بطريقة ما عن بلدي جيجاهيرتز مقارنة به ميغاهيرتز. بالإضافة إلى أنه وعد نفسه في نهاية العمل بنقل الخوارزميات إلى javascript للمتصفح.
لذلك ، كان يجب أن يبدأ البحث عن الاستراتيجيات بقرار الرسومات الأولية. يمكن العثور على وصف تفصيلي لأول مرة في لعبة Renju باللغة الروسية في كتب Sagar الشهيرة "من البداية إلى Middlegame" و Mikhail Kozhin و Alexander Nosovsky "Ringing of the Stones"
هنا . الكتب عمرها 20 عامًا بالفعل ، ولكن منذ ذلك الحين تم نشر القليل من هذه الأدبيات. المجموعة الأحدث من Dmitry Epifanov "Tiger in a cage" لعام 2015 ، للأسف ، غير متوفرة في شكل إلكتروني.
تم إجراء البحث عن قرارات الفتح المثلى وفقًا للخوارزمية التالية. في الخطوة الأولى ، تم إجراء حساب أولي دون تحديد طول الدُفعة. ثم ، لأطول الحلول ، تم إجراء التحسين: استبدال المجموعات التي تم العثور عليها مع حلول أقصر للخطوات النهائية والبحث عن فروع قرارات أقصر لجميع الحركات الوسيطة. تم إجراء التحسين حتى تم الوصول إلى الحد المستهدف لجميع فروع الحل. ثم انخفض الحد المستهدف وتم إجراء محاولة لتحسين قيمة جديدة.


لم تكن هناك مشاكل مع الظهور العمودي الأول في الشكل 3. وكانت النتيجة مجموعة كاملة من الحلول. تم حل المواقف الأكثر صعوبة بعد التحرك الرابع i8 و j10 في 31 حركة. ثم تم تعيين الحد المستهدف وهو 35 حركة لكل لعبة.


من قطري القرار ، اختار تقليديا لاول مرة 7TH. موقف أصعب تنشأ بعد الخطوة 4 G9. تم العثور على حلول طول المسموح به لمدة 6 تحركات g8 و g7.

لكن بالنسبة لهذا الخيار ، مع التحرك السادس في j9 ، لم أتمكن من إيجاد حل أقصر من 33 خطوة. لقد كانت كارثة تقريبًا. بدافع اليأس ، جربت حلول الخطوة الخامسة البديلة ، وكذلك جميع الأنواع الأخرى من الفتحات القطرية. تم حل الظهور لأول مرة ، ولكن لا يمكن العثور على أي شيء أقل من 39 خطوة لكل لعبة.
بالعودة إلى أول ظهور قطري 7 ، قام بإعادة اكتشاف الخوارزمية لتوليد جمل لمهاجمة التحركات. ونتيجة لذلك ، بدأت التحركات المؤدية إلى المراكز التي حصلت على درجة تقييم من العشرة الثالثة بشكل غير متوقع في إعطاء نتيجة وتقليل طول مسار الحل. أصبح تباين الحساب مع هذا المبلغ كبيرًا جدًا. مع وجود عمق حل يبلغ 12 خطوة ، كان هناك أكثر من 2 مليون موضع (باستثناء المواقف عند البحث عن مجموعات). استمرار تقع على 1GB من ذاكرة الوصول العشوائي المخصصة لهذه المهمة. وبالتالي ، من أجل التحقق من القرار على مفترق الطرق النهائي ، في بعض الحالات كان من الضروري تحديد المواقف بشكل منفصل من الخطوة 18.
بعد أن تم تحديد الظهور الأول للقطر السابع في 35 خطوة معينة ، يمكن للمرء الاحتفال بالفوز - لقد تم الفوز في المعركة من أجل المركز. ما زال أمامنا قدر هائل من العمل الحسابي الروتيني ، وحسابات التحركات البيضاء "غير المثالية" لاستكمال الاستراتيجية. من إجمالي حجم الإستراتيجية المثلى ، كانت الإجابة على مثل هذه التحركات نتيجة لذلك 80٪. لحسن الحظ ، تم حلها تلقائيًا بالكامل عند الحساب الأولي بعد الخطوة الثانية ، وتمت إضافة كل هذا الحجم إلى الإستراتيجية المثلى في غضون يومين.
لذلك ، تم العثور على حلول لجميع التحركات 2. لقد وضعنا أول حجر أسود في وسط الحقل ، وابدأ البحث عن حل ، ولم يكن لدينا الوقت حتى نشعر بأهمية اللحظة - تم حل الوضع الأولي في 35 حركة. تم بناء الرسم البياني للاستراتيجية الفوز الأمثل.
التحقق من أنفسنا
الخطوة التالية هي التحقق من الحل. أطفئ ذكاء الجانب المدافع تمامًا. بعد كل خطوة من خطوات Black ، يذهب White إلى أي مربع مجاني من اللوحة. يجب العثور على الموضع الذي تم الحصول عليه بعد تحرك White في الرسم البياني للقرار أو تقييمه على أنه فائز لعدد الحركات التي لا تتجاوز أطول فرع في موضع البداية. عند تقييم كل موقف ، نتحقق من المجموعة المختارة الفائزة لكل تحركات White المقبولة قبل أن يقوم Black بإنشاء القطعة النهائية - خمس مرات متتالية.
تم إجراء الفحص عدة مرات حتى اكتماله. استغرق التشغيل النهائي الخالي من الأخطاء في الوضع المفرد 14 ساعة. في أثناء عملية الفحص ، تم العثور على أخطاء وتصحيحها التي نشأت نتيجة للاختلافات في عمق البحث عن المجموعات ، والافتراضات الخاصة بالتخطي ، وتكرار المواضع المتماثلة.
أجب عن السؤال - هل القرار في 35 خطوة هو في الحقيقة الأكثر مثالية. وفقًا لبحثي ، بالنسبة لعدد من أطول فروع الفروع الرأسية ، من الممكن إيجاد حلول أكثر مثالية بطول 33 حركة. ولكن بالنسبة للقطري بعد الخطوة السادسة في j9 ، أمضى الكثير من الوقت في البحث عن حل في 33 حركة ، توسع التباين لـ Black إلى 50 حركة في كل خطوة ودون جدوى. لا يمكن إثبات عدم وجود حل في 33 خطوة بشكل صارم ، فقد انتهى الوقت المخصص للمشروع واتخذ قرار بالتوقف عند الحد المستهدف وهو 35 خطوة.
تحويل من جافا إلى جافا سكريبت
يتطلب نشر حل لمشكلة الوضوح.
لاستخدام الحل مباشرة في المتصفح ، كان مطلوبًا:- قلل من عمق البحث عن المجموعات عند تقييم المواضع إلى 17 حركة. هذا أدى إلى زيادة 2-3 أضعاف في عدد التحركات المحسوبة للاستراتيجية المثلى.
- تحويل تنسيق الرسم البياني للقرار الثنائي إلى تسلسل JSON من التحركات. هذا التنسيق هو أكثر ملاءمة في جافا سكريبت والبصرية.
- تحويل فئات جافا إلى وحدات جافا سكريبت ، باستثناء إجراءات اتخاذ القرار. هنا ، في واجهة الويب ، استبدل مكالمات خدمة الراحة بالوظائف المحلية.
قائمة فئات التطبيق:- المجلس - إدارة الحزب على متنها ، واجهة البصرية
- Vertex - أعلى الرسم البياني للقرار ، الموروثة من الموقف
- حافة - حافة الرسم البياني القرار ، ونقل المواقف التي تربط
- تخطيط - موقف ، يحتوي على مجموعة من الخطوط
- خط - خط في اتجاه معين ، يحتوي على مجموعة من الأشكال
- الشكل - شكل يحدد نوع وبدء الشكل على الخط
- نمط - أنماط من الأشكال للمقارنة عند البحث
يمكن تنزيل الحل الكامل بتنسيق JSON من ملف gomoku.json .المصادر في المستودع على جيثب .للتوضيح ، سأقدم أدناه أمثلة لأطول الألعاب التي تم الحصول عليها في العرض التوضيحي بالنقر فوق "التالي".لاول مرة قطري:
 لاول مرة عمودي:
لاول مرة عمودي:
