نموذج رياضي للعبة dobble

مستويات صعوبة القراءة

• أنا أصغر من أن أفكر

  
  
  • قواعد مقدمة اللعبة
  • كيف يفعلون ذلك؟
  • مصفوفة حادثة Dobble
  • ما اثنين من بطاقات مفقودة في اللعبة؟
  • لماذا يوجد بطاقتان أقل من الحد الأقصى الممكن في اللعبة؟
  • شكر وتقدير
  
  

• تجعلني أذكياء

  
  
  • قواعد مقدمة اللعبة
  • كيف يفعلون ذلك؟
  • ما علاقة البطاقة بها؟
  • الطائرات الإسقاطية للأوامر الصغيرة
  • مصفوفة حادثة Dobble
  • ما اثنين من بطاقات مفقودة في اللعبة؟
  • لماذا يوجد بطاقتان أقل من الحد الأقصى الممكن في اللعبة؟
  • شكر وتقدير
  
  

• كابوس

  
  
  • قواعد مقدمة اللعبة
  • كيف يفعلون ذلك؟
  • الهندسة النهائية للأطفال
  • ما علاقة البطاقة بها؟
  • الطائرات الإسقاطية للأوامر الصغيرة
  • كيفية بناء طائرة الإسقاط؟
  • مصفوفة حادثة Dobble
  • ما اثنين من بطاقات مفقودة في اللعبة؟
  • لماذا يوجد بطاقتان أقل من الحد الأقصى الممكن في اللعبة؟
  • شكر وتقدير
  
  

قواعد مقدمة اللعبة

قبل بضع سنوات اشتريت لعبة Dobble ( Dobble ، الاسم الأصلي هو "Spot It!"). إنها لعبة بسيطة وسريعة وممتعة ، أعتبرها واحدة من أفضل ألعاب الطاولة بشكل عام.

يوجد 55 لعبة في اللعبة مع 8 رموز مختلفة على كل منها. إليك شكل هذه البطاقات:

شكل 1. مثال على بطاقة اللعبة.

على كل ورقتين واحدة ورمز واحد فقط مباريات. في الشكل أعلاه ، هذا رمز قلم رصاص:

شكل 2. مطابقة الشخصيات على البطاقات.

يقوم اللاعب الذي شاهد المباراة لأول مرة بعمل على إحدى البطاقات ، اعتمادًا على جولة اللعبة. على سبيل المثال ، أخذه إلى نفسه أو يرميه إلى خصم.
غالبًا ما يؤدي هذا إلى حقيقة أن إحدى البطاقات التي يبحث عنها اللاعبون عن المباريات تتغير. لهذا السبب ، يجب عليك البحث عن تطابق جديد ، والذي قد يكون رمزًا مختلفًا تمامًا:

شكل 3 ، 4. يتم استبدال البطاقة الأولى بأخرى جديدة. الآن هناك صدفة جديدة بينهما - رمز المهرج.

كيف يفعلون ذلك؟

للوهلة الأولى ، يبدو من غير المعقول أنه على ورقتين بالضبط صدفة واحدة ، لا أكثر ولا أقل. تثار الأسئلة على الفور - كم عدد الشخصيات الموجودة في اللعبة؟ لا يمكن أن يكون عددهم أقل من اللازم (ثم سيكون هناك أكثر من تطابق على البطاقات) أو أكثر من اللازم (ثم قد لا تكون هناك أي تطابقات على البطاقات).
بالإضافة إلى ذلك ، من الواضح أن الرموز موجودة على البطاقات بترتيب خاص ، مما يضمن المطابقة الوحيدة لأي بطاقتين.

تقودنا مهارات Google الأساسية إلى موقع stackoverflow ، الذي يصف سبب حدوث ذلك: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game

تستخدم اللعبة مبادئ الهندسة المحدودة . على الرغم من وجود كلمة "علم الهندسة" في هذه العبارة ، يشير هذا المفهوم إلى علم التوافقيات أكثر من علم الهندسة. إنه يعمل مع عدد محدد من النقاط التي يمكن تحديد موقعها ، على وجه الخصوص ، في شكل طائرة إسقاطية .

البطاقات والرموز في اللعبة هي عناصر من الطائرة الإسقاطية من المرتبة السابعة. هذا يعني أنه يوجد على كل بطاقة رمز n + 1 ، والرقم الإجمالي للرموز الفريدة في اللعبة هو n ^ 2 + n + 1 ، أي 57 حرفا.

هناك طائرات من كل من الطلبات المنخفضة والعليا. على سبيل المثال ، هناك طائرة من الدرجة الخامسة. بالنسبة لها ، يتم عرض 6 رموز على البطاقة ، ويبلغ إجمالي عدد الرموز الفريدة في اللعبة 5 ^ 2 + 5 + 1 = 31. يتم استخدام الطائرة الإسقاطية لهذا التكوين في إصدار أبسط من اللعبة Doble تسمى "Doble 1،2،3" .

يتم تعيين العلاقة بين النقاط والخطوط للمستوى الإسقاط باستخدام مصفوفة الحدوث . يتم عرض مظهره في قسم "مصفوفة الوقوع للعبة Dobble".

الهندسة النهائية للأطفال

بعد وقت طويل من كتابة المقال الأصلي ، حضرت محاضرة ألكسي ساففاتيف ، حيث تحدث عن الهندسة الإسقاطية أقصر بكثير وأكثر قابلية للفهم. ولكن بما أنني لا أملك القوة أو الرغبة في إعادة كتابة نصف المقال بسبب هذا ، فإنني أوصي فقط بكتابه "الرياضيات للإنسانيات" ، إذا كانت محاولتي التي قام بها المتوحش لتفسير جهاز السيارة على الأصابع غير مفهومة أو مملة.

أولاً ، انتقل إلى ويكيبيديا وقراءة بعض المقالات. تصف المقالة الأولى مفهوم الهندسة المحدودة:

الهندسة المحدودة هي أي نظام هندسي له عدد محدد من النقاط . [1]

حتى الآن ، كل شيء بسيط. إذا قمت برسم عدة نقاط بقلم على ورقة ، فسوف يشكلون بالفعل نوعًا من الهندسة المحدودة.
مفاجأة تنتظر الكثير:

على سبيل المثال ، هندسة Euclidean ليست منتهية ، نظرًا لأن الخط Euclidean يحتوي على عدد غير محدود من النقاط ، أو بالأحرى ، يحتوي على العديد من النقاط بالضبط حيث توجد أرقام حقيقية . [1]

وهذا يعني بالنسبة لنا أن الورقة التي يتم رسم نقاطنا عليها ليست طائرة من حيث الشكل الهندسي المحدود . انها مجرد نقطة حاملة.

هناك نوعان من الهندسة على متن الطائرة: أفيني وإسقاطي . في هندسة القرابة ، يتم استخدام مفهوم التوازي المعتاد للخطوط. [1]

أذكر ما تصفه البديهيات بقسم الهندسة

هندسة أفين على متن طائرة هي مجموعة X فارغة (تسمى العناصر "نقاط") ، مع مجموعة غير فارغة من مجموعات فرعية L من X (تسمى عناصرها "مباشرة") ، بحيث:

1. لنقطتين مختلفتين ، يوجد سطر واحد فقط يحتوي على كلتا النقطتين.
2. بالنسبة للسطر ℓ والنقطة p التي لا تنتمي إلى ℓ ، يوجد سطر واحد فقط يحتوي على p بحيث يكون ℓ ∩ ℓ ′ = ∅.
3. هناك العديد من النقاط الأربع ، لا يوجد أي منها على نفس الخط. [1]

هذه البديهيات تعطينا الفرصة لفهم كيف تبدو أبسط الطائرة في الهندسة المحدودة:

أبسط طائرة أفيني تحتوي على 4 نقاط فقط ، وتسمى طائرة أفين من الدرجة الثانية . كل زوج من النقاط يحدد خطًا فريدًا ، وبالتالي فإن المستوى المشار إليه يحتوي على 6 خطوط. [1]

ليس واضحا جدا؟ هذا صحيح. إذا نظرت عن كثب إلى تعريف هندسة الأقارب ، يمكنك أن ترى أنه يعمل مع مفاهيم نظرية المجموعة (عنصر ، مجموعة ، مجموعة فرعية).
هذا يعني أن الخطوط قد لا تبدو على الإطلاق مثل الخطوط المعتادة للهندسة الإقليدية.

في الواقع ، هو عليه. إذا نظرت إلى صورة طائرة أفيني من الدرجة الثانية ، فسنرى الصورة التالية:

شكل 5. الطائرة الأثينية من الدرجة الثانية. (المصدر ru.wikipedia.org )

تبدو النقاط هنا كالنقاط السوداء العادية ، لكن الخطوط المستقيمة عبارة عن شرائح متعددة الألوان. تعتبر خطوط من نفس اللون موازية.

كما ترون ، الخطوط الموجودة هنا ليست ذات طول غير محدود. سراً ، سأقول أنه لا يوجد مفهوم للطول هنا على الإطلاق ، ويمكن أن يكون للخطوط المستقيمة أي شكل ، كما سنرى قريبًا.

من المؤكد أن٪ username٪ لا يزال يشك في أن صورة هذه الطائرة تلبي البديهيات للهندسة المتقاربة. لنفحص:

1. نأخذ 2 أي نقطة ، على سبيل المثال ، اليسار العلوي والسفلي الأيسر.
   كل من هذه النقاط تحتوي على خط أحمر واحد فقط اليسار.
   لا يحتوي الخط الأحمر الأيمن على أي من هذه النقاط ، والخطوط المتبقية تحتوي على واحدة منها فقط.
2. خذ الخط المستقيم الأحمر الأيسر والنقطة العليا اليمنى. من الواضح أن خطًا واحدًا مستقيمًا (أحمر يمين) موازٍ للخط الأحمر الأيسر ، حيث يمر عبر النقطة اليمنى العليا ، لكنه لا يمر عبر أي من النقطتين الأيسرتين.
3. يوضح الشكل بوضوح أنه بغض النظر عن 3 نقاط نأخذها ، واحدة منها تقع على خط مختلف عن الخط الذي تكمن عليه كلتا النقطتين الأخريين.
   لا يتقاطع الخطان اللذان يشكلان الأقطار المربعة للمربع ، نظرًا لعدم وجود نقاط مشتركة بينهما.

إذا فهمت جيدًا محتويات الصورة السابقة ، فستكون الصورة أكثر تعقيدًا:

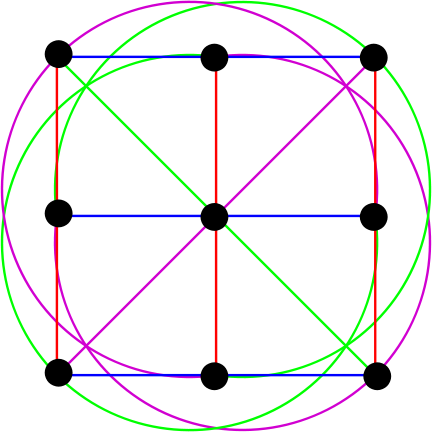
شكل 6. الطائرة الأثينية من الدرجة الثالثة. (المصدر ru.wikipedia.org )

هنا نرى 9 نقاط و 12 خطوط. نعم ،٪ اسم المستخدم٪ ، هذه الأشكال البيضاوية هي في الواقع خطوط مستقيمة من حيث الهندسة المحدودة.
الأشكال من نفس اللون هي خطوط متوازية. من الصعب ملاحظة ذلك ، لذلك نقسم الصورة إلى عدة:

الطائرة رقم 1	الطائرة رقم 2	الطائرة رقم 3	الطائرة رقم 4

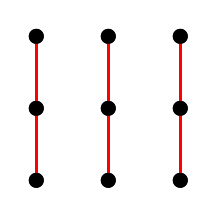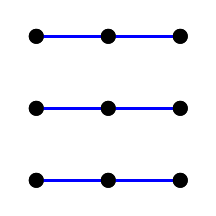شكل 7. خطوط مستقيمة موازية للطائرة affine من الدرجة الثالثة.

هنا ، يستغرق التحقق من تنفيذ البديهيات وقتًا أطول قليلاً:

1. نأخذ 2 أي نقطة ، على سبيل المثال ، العلوي الأيمن والسفلي المركزي. من خلالهم يمر واحد فقط من الخطوط الأرجواني.
2. خذ الخط الأحمر الأيسر والنقطة اليمنى السفلى. على غرار طائرة من الدرجة الثانية ، يمر خط أحمر واحد فقط من هذه النقطة ، لكنه لا يمر عبر أي من النقاط اليسرى الثلاثة.
3. هنا الأمر أكثر تعقيدًا قليلاً من حالة الطائرة من الدرجة الثانية. يوضح بيان البديهية أنك بحاجة إلى العثور على مجموعة واحدة على الأقل (غير فارغة) من أربع نقاط ، حيث لا يوجد ثلاثة على أكثر من سطر واحد.
   من الواضح ، 12 مجموعة مع ثلاث نقاط من خلالها الخطوط في الشكل لا تفي بهذا الشرط. لكنه يرضي ، على سبيل المثال ، مجموعة من أربع نقاط ركنية.

في حالة أكثر عمومية ، توجد طائرة ذات رتبة محدودة من الترتيب n لها نقاط n ^ 2 وخطوط n ^ 2 + n ؛ كل سطر يحتوي على نقاط n ، وكل نقطة تنتمي إلى خطوط n + 1 . [1]

مع الانتهاء من هندسة القرب ، نمر إلى النوع الثاني من الهندسة على متن الطائرة - الإسقاطية.

على العكس من ذلك ، في الهندسة الإسقاطية ، يتقاطع أي سطرين عند النقطة الوحيدة الممكنة ، وبالتالي لا توجد خطوط موازية. [1]

تصف الجملة السابقة البديهية الثانية للهندسة الإسقاطية. الأول والثالث هي نفسها كما في أثينا.

نظرًا لأن البديهية الثالثة تتطلب وجود أربع نقاط على الأقل ، يجب أن تحتوي الطائرة على 7 نقاط على الأقل من أجل تلبية شروط البديهيات الأولين. في هذا أبسط من الطائرات الإسقاط هناك أيضا 7 خطوط. كل نقطة تنتمي إلى ثلاثة خطوط ، وكل سطر يحتوي على ثلاث نقاط. وغالبا ما تسمى هذه الطائرة الإسقاطية "طائرة فانو" . [1]

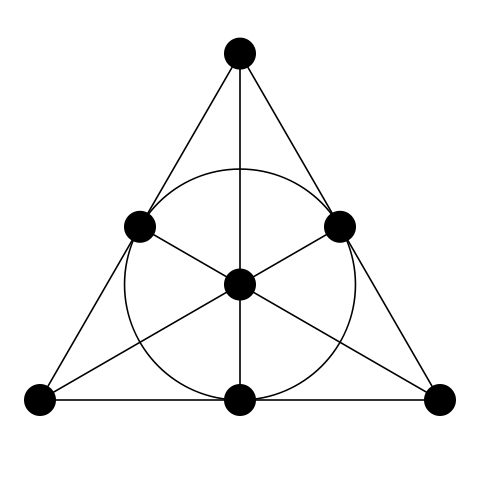
شكل 8. طائرة فانو. (المصدر en.wikipedia.org )

في هذا الشكل ، يصعب فهم جميع الأسطر السبعة على الفور ، لذلك هنا إصدار مهر لنفس الطائرة:

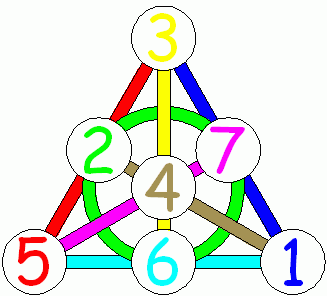
شكل 9. فانو الطائرة مع خطوط ملونة. (المصدر mathpuzzle.com . تستخدم بإذن من Ed Pegg Jr. )

لذلك ، فإن طائرة فانو هي طائرة إسقاطية ذات ترتيبين مع 7 نقاط و 7 خطوط.

ما علاقة البطاقة بها؟

ماذا يحدث إذا أعدنا صياغة 2 من البديهيات للهندسة المحدودة ، مع استبدال "الخط" بـ "الرمز" و "النقطة" بـ "البطاقة"؟

والنتيجة هي هذه:

1. لاثنين من بطاقات مختلفة ، هناك رمز واحد فقط ، والذي يظهر على كل من البطاقات.
2. بالنسبة إلى رمزين مختلفين ، لا يوجد سوى بطاقة واحدة تحتوي على كلا الرمزين.

الآن ، بناءً على هذه المعرفة ، لنرى كيف سيبدو دوبل في أبسط الحالات. سيكون لها 7 بطاقات و 7 أحرف ، وستحتوي كل بطاقة على 3 أحرف (حيث تتقاطع 3 خطوط عند نقطة واحدة):

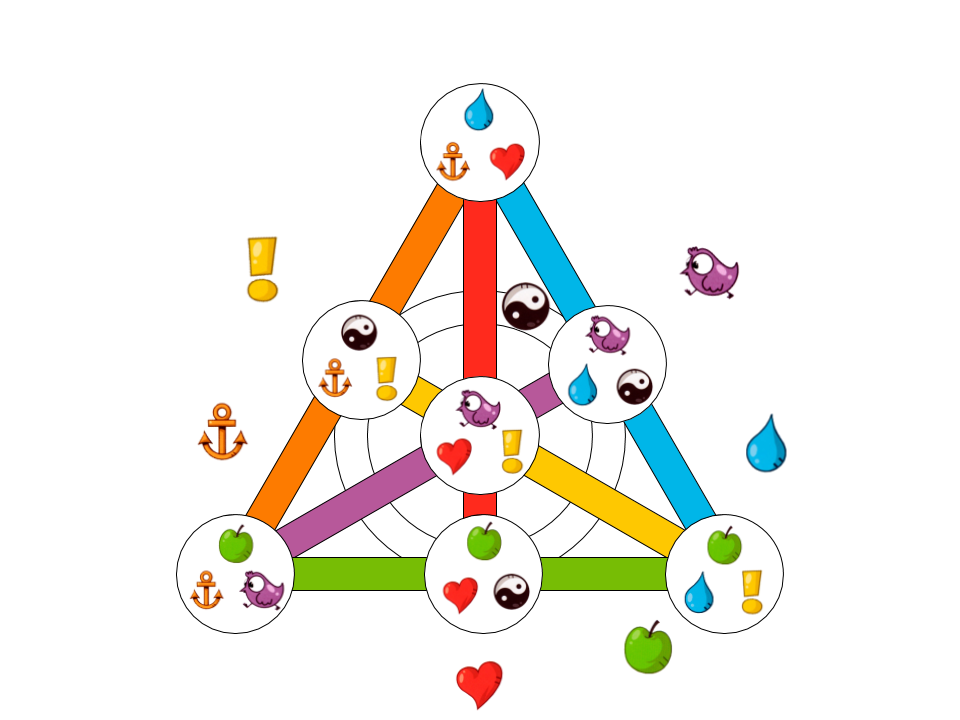
شكل 10. مثال على أصغر مجموعة ممكنة من البطاقات لـ Dobble.

يتم استخدام الأحرف السبعة التالية هنا:

، ، ، ، ، ،
بغض النظر عن أي ورقتين نأخذهما ، سيكون لديهم رمز مشترك ، مصور بجوار السطر الذي توجد عليه كلتا الورقتين.
على سبيل المثال ، تحتوي البطاقة الموجودة في الركن الأيسر السفلي والبطاقة الموجودة في منتصف الجانب الأيمن على رمز مشترك . يظهر بجانب السطر. .

الطائرات الإسقاطية للأوامر الصغيرة

على Wolfram ، يمكنك العثور على عرض مرئي للطائرات الإسقاطية للأوامر الصغيرة: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
تم تصميمه كمستند بتنسيق CDF (تنسيق المستند القابل للحساب) ، الذي تحتاج إلى تثبيت CDF Player عليه .

فيما يلي مثال لطائرة إسقاطية من النظام 3:

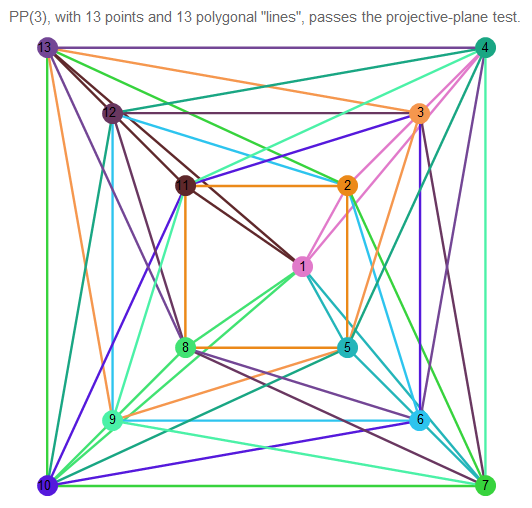
شكل 11. صورة من الطائرة الإسقاطية من 3 أوامر.

من الصعب فهم ما يحدث ، لذلك خذ خطين اعتباطيين:

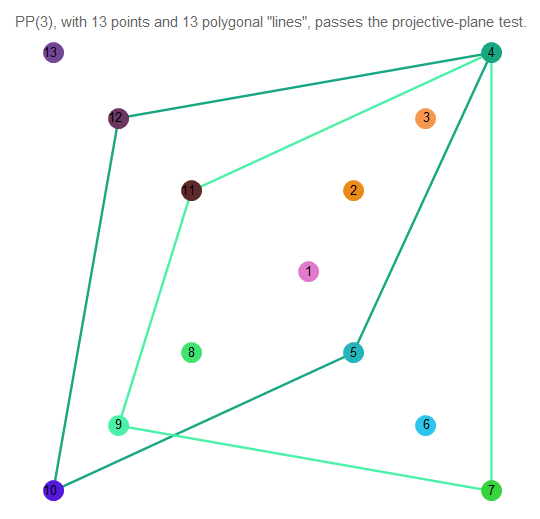
شكل 12. تقاطع سطرين من الطائرة الإسقاطية من الدرجة الثالثة.

كما نرى ، فهي تتقاطع تمامًا عند نقطة واحدة. الخطوط نفسها تحتوي على 4 نقاط.

للتأكد من مرور 4 أسطر عبر كل نقطة ، يجب عليك تبديل أزواج الخطوط المعروضة في مستند تفاعلي والتركيز على نقطة ما.

يتم عرض الطائرات الإسقاطية للطلبيات العليا في الأشكال أدناه.

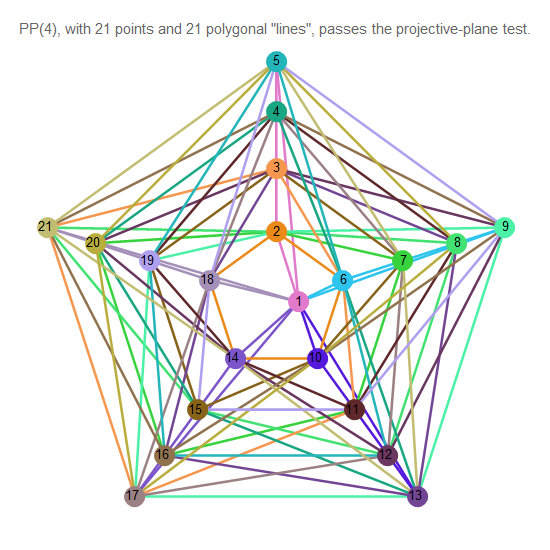
شكل 13. طائرة إسقاطية من أجل 4

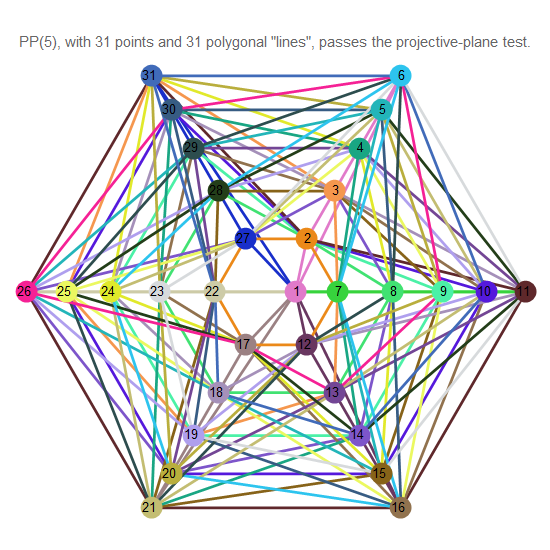
شكل 14. الطائرة الإسقاطية للنظام 5

شكل 15. طائرة إسقاطية من أجل 7

في التسلسل أعلاه ، لا توجد صورة للطائرة الإسقاطية من المرتبة السادسة. هذا ليس خطأ.

على الرغم من أن Wolfram يولد تمثيلًا بيانيًا لمثل هذا الهيكل ، إلا أنه لا يرضي البديهيات في الهندسة الإسقاطية ، ولا يمثل مستوى إسقاطي.

من المفترض ، ولكن لم يثبت بعد ، أن ترتيب الطائرة المحدودة هو دائمًا قوة رئيسية . [1]

كيفية بناء طائرة الإسقاط؟

يبدو الرسم البياني للطائرة الإسقاطية ممتعًا وواضحًا ، ولكن كيف يمكن العثور على مزيج من النقاط بحيث يمتلك الخصائص المذكورة أعلاه؟

أسهل طريقة هي زيارة المواقع التي تستضيف بيانات محسوبة مسبقًا للطائرات الإسقاطية ذات الطلبات المختلفة.

على سبيل المثال ، بالنسبة للطائرة الإسقاطية للنظام 7 ، يمكنك زيارة الصفحة التالية: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
ويرد مصفوفة من الأرقام هناك. الخطوط عبارة عن بطاقات (نقاط) من حيث Dobble. الأرقام في الأسطر هي الأرقام التسلسلية للأحرف (الأسطر) ، بدءًا من الصفر ، والتي يتم رسمها على كل بطاقة (تمر عبر هذه النقطة).

يمكنك أيضًا استخدام خدمات الحزم الرياضية ، مثل Matlab ، لإنشاء مصفوفة الحدوث للطائرة الإسقاطية. [2] [3]

مصفوفات الإصابة

مصفوفة الوقوع هي أحد تمثيلات الرسم البياني التي تشير إلى العلاقات بين العناصر الموضحة في الرسم البياني (الحافة (القوس) والرأس). تتوافق أعمدة المصفوفة مع الحواف ، والصفوف إلى القمم. تشير القيمة غير الصفرية في خلية المصفوفة إلى العلاقة بين الرأس والحافة ( حدوثها ). [2]

أحد أبسط أمثلة مصفوفة الوقوع يمكن أن يكون مصفوفة 2 × 1 للرسم البياني غير الموجه لرؤوسين متصلين بحافة واحدة:

شكل 16. رسم بياني غير موجه من رأسين متصلين بحافة واحدة ، ومصفوفة الإصابة.

مثال أكثر تعقيدًا للرسم البياني ومصفوفة الإصابة:

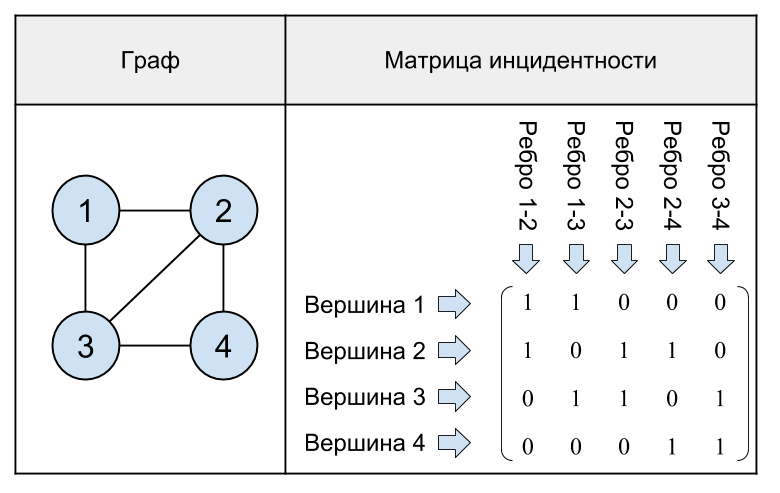
شكل 17. رسم بياني غير موجه مع 4 رؤوس ومصفوفة الإصابة.

كما يتضح من المثال الأخير ، في مصفوفة الوقوع في الرسم البياني في كل عمود هناك وحدتان بالضبط ، لأن حافة واحدة تربط اثنين من القمم.
المستوى الإسقاطي عبارة عن رسم توضيحي ، لأن سطر واحد (حافة) يربط عدة نقاط (القمم). لذلك ، في مصفوفة الحدوث لمستوى الإسقاط ، تحدث الوحدات في كل عمود n + 1 مرات ، حيث n هو ترتيب المستوى الإسقاطي.

للطائرة فانو هو مبين في الشكل. 9 ، سوف تكون مصفوفة الإصابة على النحو التالي:

شكل 18. مصفوفة وقوع طائرة فانو.

لتبسيط الإدراك ، لا يتم عرض الأصفار ، ويتم استبدال الوحدات بالرمز X.
في هذا التمثيل للطائرة الإسقاطية ، يكون مبدأ ازدواجية النقاط والخطوط واضحًا - يمر الخط بثلاث نقاط بالضبط ، وفي الوقت نفسه ، تنتمي النقطة إلى ثلاثة خطوط بالضبط.

بناء طائرة الإسقاط بالقوة الغاشمة

المعرفة الحالية حول خصائص مصفوفة الوقوع كافية لتصميمها للطائرة الإسقاطية من أي أمر n. للقيام بذلك ، يمكنك استخدام الكود الكاذب التالي:

          n+1 ,          n+1 ,                                ,                

بعد هذه الخوارزمية ، نحصل على مصفوفة متماثلة لطائرة Fano:

شكل 19. مصفوفة حدوث طائرة Fano التي تم إنشاؤها بواسطة خوارزمية الكود الزائف.

هذه المصفوفة لا تتطابق مع المصفوفة السابقة. في الواقع ، لا يهم.
إن التقليب في أي صفين من مصفوفة الوقوع يعادل إعادة ترقيم رؤوس الرسم البياني.
إن التقليب في أي عمودين من مصفوفة الوقوع يعادل إعادة ترقيم حواف الرسم البياني (إذا كانت مرقمة مسبقًا).

مصفوفة حادثة Dobble

بالنسبة للعبة Dobble في مصفوفة الوقوع ، تكون الصفوف مسؤولة عن البطاقات ، وتكون الأعمدة مسؤولة عن الشخصيات الموجودة عليها.
وبالتالي ، فإن التقليب في أي عمودين من مصفوفة الوقوع يعادل التغيير في تسلسل الحروف على البطاقة. ومع ذلك ، فإن الرموز الموجودة على البطاقة غير مرتبة ، لذلك لا تؤثر هذه العملية على مظهر البطاقات.
إعادة ترتيب سطرين تعني أنه على جميع البطاقات ، يحل الرمزان المقابلان محل بعضهما البعض.

العملية الأخيرة تغير مظهر البطاقات ، مما يعني أن مجموعة الشخصيات التي نراها في اللعبة هي مجرد واحدة من المجموعات الممكنة.
عدد مجموعات الأحرف لبطاقة معينة هو مزيج من 57 عنصرًا و 8 عناصر دون تكرار. يتم حسابه بواسطة الصيغة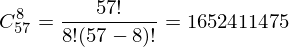

يتم عرض مصفوفة الإصابة في Dobble في الجدول أدناه. يتم نقله ، أي الصفوف هي رموز ، والأعمدة عبارة عن بطاقات (الصورة قابلة للنقر). لا يسمح لك Habr بإدراج صورة بالحجم والجودة المرغوبة ، وبالتالي فإن خيار الحجم الكامل هو رابط منفصل: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble٪20incidence٪20matrix.png

شكل 20. مصفوفة حدوث لعبة Dobble.

ما اثنين من بطاقات مفقودة في اللعبة؟

في المجموع ، يحتوي الجدول الذي يحتوي على مصفوفة الحدوث للعبة على 57 صفًا و 55 عمودًا. هذا يعني أنه يمكن أن تحتوي اللعبة على ورقتين إضافيتين.
هذا يعني أن الشخصيات التي يجب أن تكون على هذه البطاقات أقل شيوعًا في اللعبة من البقية. يظهر عدد الشخصيات في اللعبة في العمود الأخير من الجدول.

عدد الأحرف من البطاقات المفقودة هو كما يلي:

• ، ، ، ، ، ، ، ، ، ، ، ، و
  (إجمالي 14 حرفًا) يحدث 7 مرات.
• يحدث 6 مرات.

كيف تبدو البطاقات المفقودة؟ للإجابة على هذا السؤال ، خذ أيًا من الأحرف أعلاه في مصفوفة الوقوع (باستثناء رجل الثلج) ، ثم ضعه على البطاقة المفقودة (على سبيل المثال ، العمود قبل الأخير).

ثم نجد جميع البطاقات (الأعمدة) التي يظهر عليها هذا الرمز. هذا يعني أنه في جميع هذه البطاقات تتزامن الرموز ، ولا يمكن أن تكون هناك مطابقات أخرى.

نظرًا لأن هذه البطاقات تحتوي بالفعل على تطابق مع الحرف المحدد ، شطب من العمود ما قبل الأخير جميع الأحرف التي تظهر على البطاقات الأخرى.
الأحرف المفقودة التي لم يتم استبعادها ، وقم بتكوين أحرف إحدى البطاقات المتبقية. نظرًا لأنه تبين أنها بالضبط 8 ، يتم تحديد نوع البطاقة المفقودة الثانية بشكل لا لبس فيه.

هذه هي البطاقات 2:

شكل 21- وهناك نوع محتمل من البطاقات المفقودة هو الرقم 56 ورقم 57.

يبقى أن نجيب على السؤال الأخير - هل يؤثر غياب هذه البطاقات على خاصية تزامن رمز واحد بين بطاقتين (أي فجأة لا توجد تطابقات بين بعض البطاقات)؟

الجواب واضح ، إذا كنت لا تزال تنظر إلى مصفوفة وقوع اللعبة - لا ، لا. بين أي ورقتين (الأعمدة) لا تزال هي الصدفة الوحيدة.

لماذا يوجد بطاقتان أقل من الحد الأقصى الممكن في اللعبة؟

في البداية ، لم تكن القواعد الخاصة بالألعاب المصغرة الخمس موجودة في الكتيب ، ولكن في خمس بطاقات منفصلة. في الوقت نفسه ، يمكن طباعة 60 بطاقة فقط. لذلك ، قرر مؤلفو اللعبة إزالة ورقتين ، بحيث تحول في النهاية إلى 55 ورقة مع رموز + 5 بطاقات مع قواعد. (شكر خاص لـ Guillaume Gille-Naves للتوضيح.)

شكر وتقدير

أعرب عن امتناني لشبكة متاجر ألعاب الطاولة "Igroved" لمساعدتهم في كتابة المقال.
بفضل Ed Pegg Jr لتوفير صورة طائرة Fano.
بشكل منفصل ، أود أن أذكر anonymus و Master للمساعدة في التحقق من المقال.
أشكر متجر "Table City" على مساعدته في التحضير لنشر المقال.
من كل قلبي ، أشكر مؤلفي اللعبة إيغور بولوتشين ، دينيس بلانشوت ، غيوم غيل نافيس ، وكذلك أسمودي على حقهم في استخدام الصور من اللعبة.