ثلاثية متوازنة
أنا أعمل على محاضرات مبادئ هندسة الكمبيوتر لجامعتنا. وكواجب أود أن أقترح على طلابي بناء آلة بسيطة قابلة للبرمجة تعمل في
الثلاثية . السبب الرئيسي هو المتعة: كمحاضر يجب أن أحضر بعض الترفيه ، وإلا لن أستمع إلي. الى جانب ذلك ، من المهم لأسباب تاريخية. أي "لماذا؟" سيتم الرد على الأسئلة "لأنني أستطيع".
تصف هذه الصفحة الأساسيات ذاتها ، ولن تتجاوز مجرد إعلان ternary البسيط (وتطبيقه للأجهزة). ترقبوا المزيد.
لقد اخترت النظام الثلاثي المتوازن: كل سورة تمثل واحدة من ثلاث حالات ممكنة ، -1 أو 0 أو 1. ويمكن العثور على وصف شامل للغاية لهذا النظام
هنا .

لبنة البناء الأساسية: المضاعف الثلاثي
التجريد
الكتلة الوحيدة التي سيتم استخدامها في جهاز الكمبيوتر الخاص بي هي المضاعف الثلاثي.
يمكن اعتباره مربعًا أسودًا بخمسة دبابيس: يستقبل دبوس التحديد إشارة ثلاثية (إما -1 أو 0 أو 1) ، ثم يوجد مفتاح صغير داخل الصندوق يصل دبوس الخرج بواحد من ثلاثة دبابيس إدخال inN ، inO أو inP.
عادة ما يتم تصويره كما هو موضح هنا:
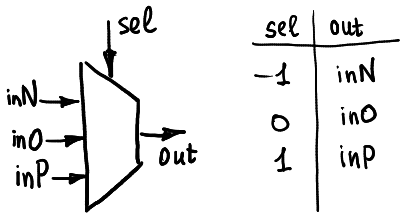
يعمل مزيل تعدد الإرسال الثلاثي بطريقة مماثلة: اعتمادًا على دبوس المحدد ، يتم توصيل إدخال واحد بواحد من ثلاثة دبابيس إخراج ممكنة. لاحظ أنه في أجهزتي أستخدم مفاتيح CMOS التناظرية. هذه هي ثنائية الاتجاه ، لذلك يمكن استخدام الأجهزة كل من المضاعف و demultiplexer. لكن على أي حال ، في الوقت الحالي ، لا أستخدم إمكانات إلغاء تعدد الإرسال.
تنفيذ الأجهزة
اقترح التصميم الأساسي بواسطة
Shaos .
الشيء الوحيد الذي فعلته هو إنشاء نسخة SMD من TRIMUX. يمكن شراء مفاتيح dg403 المثبتة على الأسطح مقابل 50p للقطعة الواحدة في الصين.
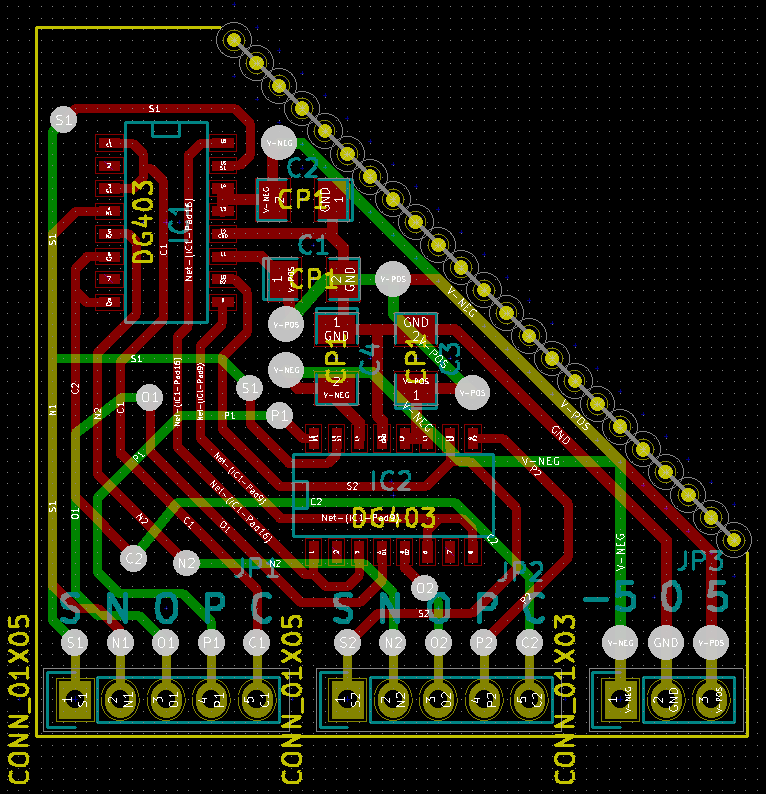
قبل أن أجد هذا التصميم ، حاولت استخدام مجموعات من cd4007 و cd4016. نجحت ، ولكن الأجهزة مرهقة وقبيحة. توفر محولات DG403 إمكانات حقيقية للحوسبة الثلاثية دون أي تكرار مثل استخدام ثنائي بت وحظر أحد التكوينات الأربعة.
يمكن إنشاء مُضاعِف ثلاثي ثلاثي باستخدام DG403: يستقبل أحد ICs مدخلات الطاقة من 5 إلى 0 فولت ، بينما يتم تشغيل الآخر مع 0 فولت إلى 5 فولت ، ويسمح باستخدام إشارات ثلاثية تمثلها ثلاث توترات -5 فولت ، 0 فولت و 5 فولت ، على التوالي. لا يستخدم هذا التصميم سوى نصف دبابيس dg403 ، لذلك من الطبيعي إنشاء لوحة بمضاعفين.
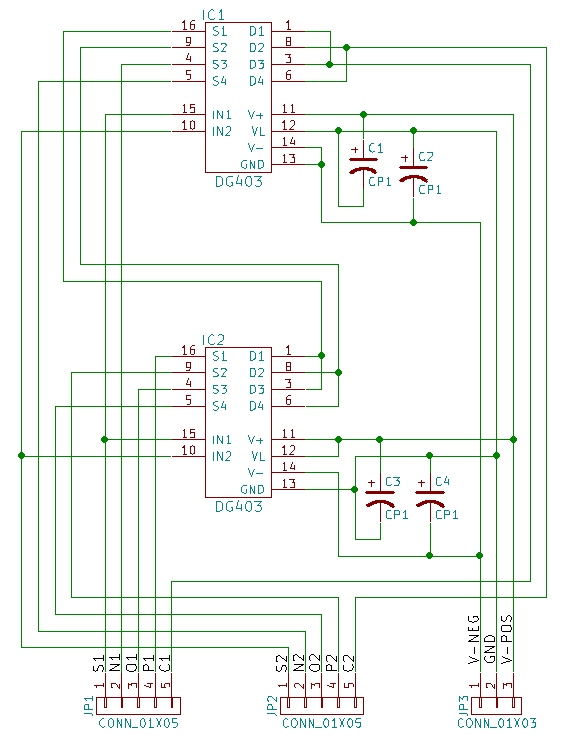
لا تتردد في الاتصال بشاوس
هنا . رجل مذهل ، وبدلاً من التكهن بفوائد الثلاثية ، قام بتصميم وتصنيع الشهادات المرحلية الثلاثية الخاصة به!

كيفية استخدامها؟ وظائف أحادي
دعونا نغفل وظيفة الهوية التي يمكننا الحصول عليها عن طريق إعطاء -1.0 و 1 إلى دبابيس الإدخال المقابلة من المضاعف.
للبدء ، دعنا نزيد إشارة الدخل A عن طريق حساب A + 1 (بالطبع ، في الحلقة -1،0،1):
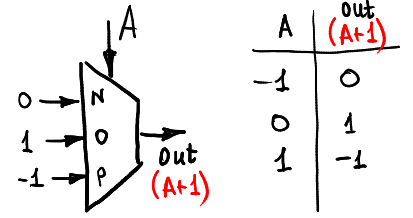
إليك الطريقة التي يمكن بها تقليل الإدخال:
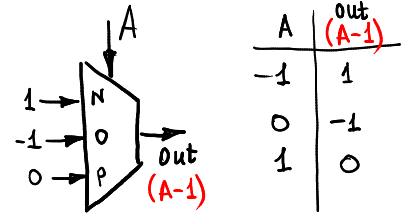
دعنا نحسب الحد الأقصى (A ، 0):
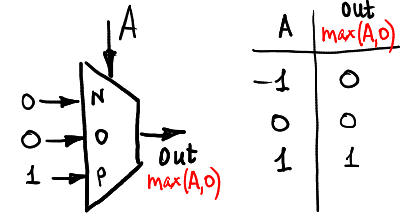
والدقيقة (A ، 0):
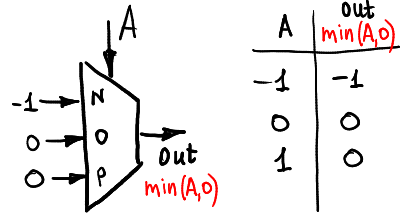
وظائف حجتين: نصف الأفعى
A + B
لذلك ، يتيح لنا مُضاعِف مضاعف حساب أي وظيفة أحادية. لحساب وظيفة الوسيطتين ، نحتاج إلى استخدام ثلاثة أو أربعة معددات. على سبيل المثال ، إذا أردنا حساب مجموع إشارتين A و B (لا يزالان في الحلقة -1،0،1) ، فيمكننا استخدام هذا المخطط:
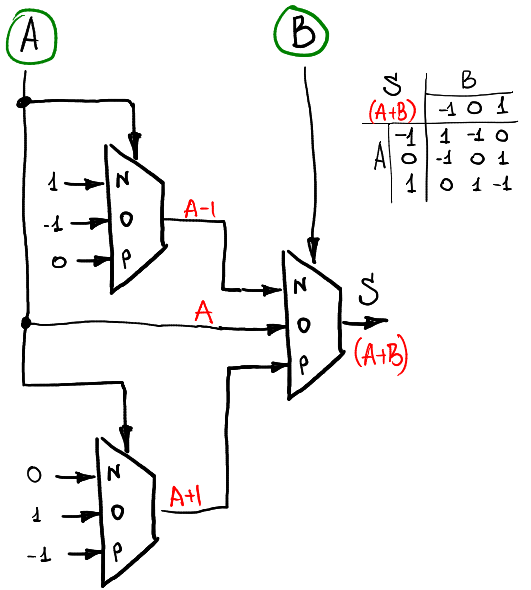
هناك طبقتان من المضاعفات: الأولى تحسب الدوال الأحادية لـ A ، والطبقة الثانية تجمعها وفقًا لـ B.
إجماع
إذا أردنا حساب دالة الإجماع لإشارتين ثلاثية (إجماع يساوي -1 إذا كانت A = B = -1 ، تساوي 1 إذا كانت A = B = 1 وكانت الصفر على خلاف ذلك) ، فيمكننا القيام بذلك مثل هذا:
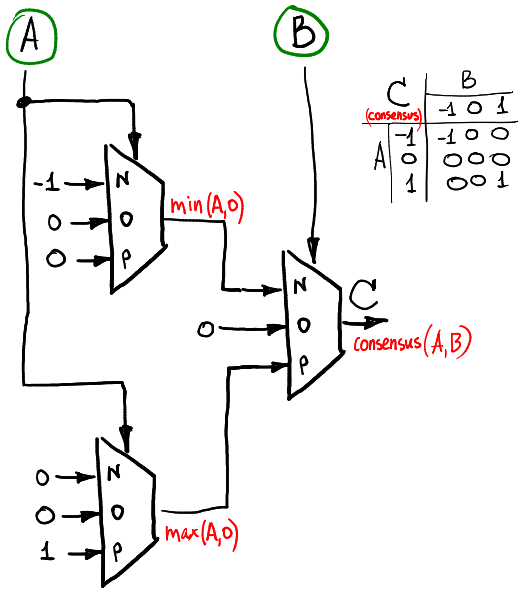
تنفيذ الأجهزة
في الواقع ، أنشأنا للتو
نصف الأفعى . بالنسبة إلى اثنين من المدخلات A و B ، فإنه يحسب اثنين من النواتج S و C المتعلقة A + B = S + 3 * C. S هي المجموع و C هي علامة الحمل.
دعونا اختبار التصميم! مؤشر LED الأحمر يعني -1 ، يعني إيقاف ، 0 ، مؤشر LED أخضر يعني 1. وهكذا ، تخبرنا هذه الصورة أن S = -1 ، C = 1 ، أو ، 1 + 1 = -1 + 3 * 1:

هنا هو الجدول الذي يسرد جميع الحالات التسع المحتملة من نصف الأفعى لدينا. تعطي كل خلية قيمًا مطابقة لـ S و C. يتم توفير ارتباط لصورة لكل خلية.
ثلاث حجج: الأفعى الكاملة
على النقيض من النصف الأفعى ، يتلقى
الأعلاف الكاملة ثلاثة مدخلات A و B و Cin ويحسب مخرجات S و Cout المرتبطة بـ A + B + Cin = S + 3 * Cout.
مجموع ثلاثة trits
إذا كنا نريد حساب مجموع A + B + Cin ، فإن الفكرة هي نفسها كما كانت من قبل: نحن نستخدم إعداد المدخلات طبقة تلو الأخرى. تستقبل الطبقة الأولى A كمدخل ، أما الثانية فتستخدم B وآخر طبقة أحادية الإرسال تستخدم Cin. فيما يلي طريقة واحدة ممكنة لحساب الإخراج S:
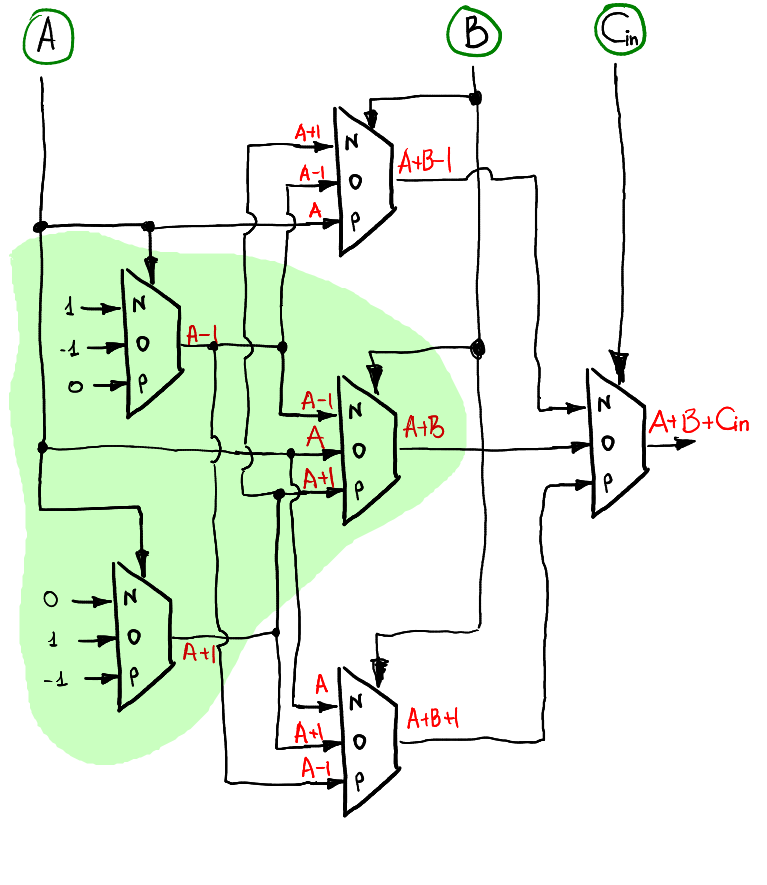
لاحظ أنه عندما يكون Cin = 0 ، فإنه يتصرف تمامًا بنفس طريقة سلوك نصف الأفعى ، لذلك فمن الطبيعي أن نرى تضمين (تم تمييزه باللون الأخضر) في مخططات النصف الآخر في الأفعى الكاملة.
الفائض (حمل العلم)
يمكن حساب ثقل الفائض بنفس طريقة تلو طبقة. ويشمل أيضا نصف الأفعى!
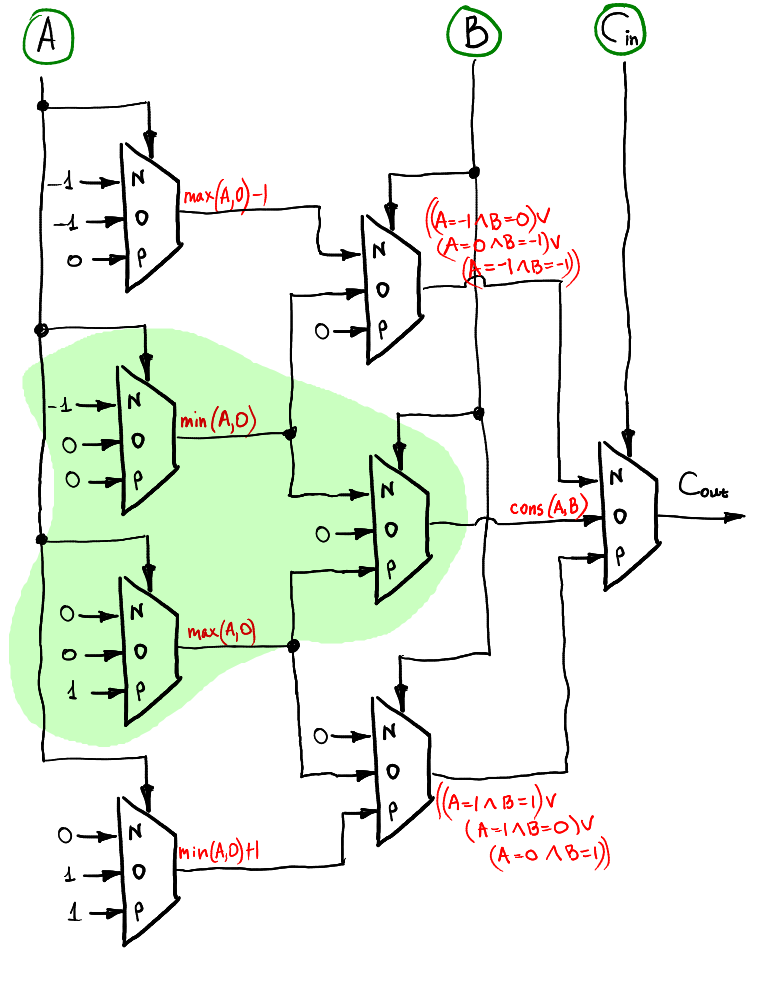
التحقق من صحة الأجهزة
هذه المرة كنت كسولًا جدًا في استخدام الألواح لاختبار الأفعى الكاملة ، لذلك قمت بعمل ثنائي الفينيل متعدد الكلور ذي الطبقة الواحدة:

ومن هنا بعد أن تم حفر النحاس:

ثلاثة الجداول التالية تسرد جميع الحالات الـ27 الممكنة من الأفعى الكاملة. كما كان من قبل ، الصور متاحة لكل ولاية. لاحظ أن الجدول الأوسط (Cin = 0) هو نفسه تمامًا بالنسبة للنصف الآخر.
ميزة الأفعى الكاملة فيما يتعلق بالنصف الأعمى هي إمكانية تكديس إضافات متعددة حتى نحصل على عدد كاف من الامتيازات لتمثيل الرقم الذي نريده.
هنا كومة من اثنين من الإضافات:

وهنا كيف يحل -4 + 2 (أقل طريقة مهمة موجودة على اليسار):

بالطبع ، نحن لسنا بحاجة إلى لوحة إعلان كاملة لأقل سمة مهمة (ليس لدينا علامة حمل لإدخال الأقلية أهمية) ، فإن نصف الأفعى يكفي.
الخاتمة
هذه هي نهاية مقدمة الحوسبة الثلاثية. ترقبوا الساعات والعدادات والذاكرة وأكثر!