أننا يجب أن بناء الطريق. الجزء 1

يقتصر مسار الرحلة اليومي لمعظمنا على السفر من المنزل إلى العمل والعودة. العقبة الأكثر صعوبة التي يمكن أن تبطئ حركتنا هي الاختناقات المرورية. ولكن في بلدنا هناك عدد كبير من الأماكن حيث يمكنك فقط الحصول على سيارات خاصة.

يعتبر هذا النقل جيدًا إذا كنت لا تحتاج إلى نقل كميات كبيرة من البضائع أو السفر إلى هذه المناطق التي يتعذر الوصول إليها بشكل منتظم. ثم يجب أن نفكر بالفعل في بناء البنية التحتية ، والتي يمكن نقلها على النقل المدني المعتاد.

ومن الجيد إذا كان التعقيد الكامل لتصميم طريق مستقبلي يكمن في إيجاد مسطرة وقلم رصاص لرسم خط مستقيم على الخريطة يربط عدة أشياء. لكن ، للأسف ، واقعنا مختلف تمامًا عن هذا. ماذا لو كانت التضاريس التي تحلق فوقها تشبه قطعة جيدة من الجبن السويسري؟

منذ أكثر من عام ، كنا نعمل مع زملاء من مختبر أبحاث التصميم الرقمي لإنشاء أداة يمكنها بناء شبكات اتصالات مختلفة في الوضع التلقائي. لمزيد من التفاصيل ، مرحبا بكم في القط.

كيف بدأ كل شيء

عادة ، تعود الرحلات إلى هذه الأماكن النائية إلى فوائد مالية معينة. رغم أنه من المعروف غالبًا أن تطوير هذه المناطق سيحقق أرباحًا جيدة ، فلماذا لا يوفر المال على الأشياء التي يمكن القيام بها دون صعوبات خاصة؟ ماذا لو سمح لنا طريق مصمم بطريقة أكثر كفاءة بعدم بناء عدة كيلومترات إضافية من الطريق السريع؟

لكن من الواضح أن توفر الطرق لتلقي أي ربح كبير ليس كافياً. وبشكل أساسي يتم إحضاره فقط بواسطة الرواسب المعدنية. لذلك ، بالإضافة إلى الطرق ، من الضروري تصميم شبكة من خطوط الأنابيب المختلفة ، وشبكة من خطوط أنابيب المياه ، وشبكة من خطوط الطاقة مع محطات الكهرباء الفرعية الموضوعة بشكل صحيح. يمكن تعيين كل هذه البنية التحتية ككائنات خطية.

وعندما يواجه مهندس مهمة تصميم شبكة اتصالات على الأرض مع ظروف هندسية وجيولوجية معقدة ، تقع عليه مهمة تحليلية معقدة بشكل لا يصدق.

كيف لا تصل الى منطقة الفيضان النهر؟ كيفية تقليل المسار على التربة دائمة التجمد؟ كيف يمكنك توفير كمية من وسادة الرمل عند وضع طريق من خلال مستنقع؟ أين يمكن الحصول على الرمل لهذه الوسادة؟

هذه ليست سوى جزء صغير من الأسئلة التي يسألها المهندس أثناء العمل ، ومع ذلك لا تزال بحاجة إلى مراعاة مختلف GOSTs و SNiPs. وكذلك ، إذا كنت ترغب في توصيل كائنين فقط ، وإذا كان هناك بضع عشرات الكائنات؟

لذلك ، فإن صناعة التصميم في حاجة ماسة إلى أداة يمكنها حساب تكلفة الأشياء الخطية التي صممها المهندس والقدرة على بنائها في الوضع التلقائي.

البيانات

أول شيء كان علينا التعامل معه عندما بدأنا المهمة هو البحث عن البيانات. ما هي البيانات المطلوبة؟ أين يمكن الحصول عليها؟ وإذا كان يمكن حل السؤال الثاني بمساعدة المستخدم ، ثم لفهم السؤال الأول الذي نحتاجه إلى تحليلات جدية.

وتتطلب بيانات الحساب الصحيح كثيرًا بالفعل - بدءًا من أكثر العلامات التي يتم تمييزها في المنطقة التي تتميز بها البحيرات والأنهار ، والمستنقعات المختلفة ، وكذلك المناطق الكارستية ، التي يوصى بشدة بعدم بنائها بسبب تهديد الانهيار. لذلك ، بالإضافة إلى المناطق التي يمكن رؤيتها من القمر الصناعي ، هناك حاجة أيضًا إلى بيانات من الدراسات الجيولوجية للمنطقة.

لكن لا تقتصر جميع البيانات على الأشياء الطبيعية في بلدنا. هناك أيضًا مجموعة من الأشياء التي تم إنشاؤها بواسطة الإنسان. على سبيل المثال ، في حالة إنشاء الطرق ، يمكننا استخدام الطرق التي تم إنشاؤها مسبقًا. ولكن في بناء خطوط الأنابيب ، لا يزال استخدام البنية التحتية الحالية بعيدًا عن الإمكان دائمًا. منذ اتصال خط أنابيب جديد بشبكة موجودة قد لا يمر حساب هيدروليكي.

بالإضافة إلى إعادة استخدام ما تم إنشاؤه من قبل الإنسان ، يجب على المرء أيضًا أن يأخذ في الاعتبار القيود المختلفة على الإنشاء بالقرب من أي كائنات ، على سبيل المثال ، لبناء خطوط الكهرباء ، تحتاج إلى أن تأخذ في الاعتبار المسافات البادئة من أماكن سكن الإنسان اعتمادًا على الجهد على خط الطاقة نفسه.

لكن ليس صحيحًا تمامًا النظر في حساب المشكلة فقط على متن طائرة ، لأنه بالإضافة إلى التضاريس المسطحة ، هناك مناطق ذات اختلاف كبير في الارتفاع ، والتي لا يمكن إجراء البناء عليها أيضًا.

يعد الحصول على البيانات على التضاريس عملية أبسط بكثير من البيانات المتعلقة بتحديد المناطق والبنية التحتية الحالية. لتبسيط التطوير ، نستخدم بيانات الارتفاع المفتوحة SRTM (Shuttle Radar Topography Mission) التي يمكن لأي شخص الحصول عليها.

لذلك ، لدينا البيانات ، ونعرف أين يمكننا البناء ، وحيث لا يمكننا البناء ، هناك تكاليف بناء لمناطق مختلفة من التضاريس. لدينا منطقة ، ولديها مجموعة من الأشياء التي نريد توصيلها بشبكة اتصال واحدة. من الناحية الرياضية ، سيبدو هذا كبحث عن حل لمشكلة شتاينر.

قليلا من الرياضيات

من المعروف أن كل صيغة تقلل من عدد القراء إلى النصف ، لذلك قمنا بتقليل هذا القسم بشكل كبير ...

من أجل تحسين مسار المنشأة الخطية المصممة ، من الضروري أن تكون قادرًا على حساب تكلفة الإنشاء. يمكن تمثيل كل كائن خطي على شكل خط متعدد $$$L = \ {A_i ، B_i \} _ {i = 0} ^ n$ تتكون من شرائح $$$AB_ {i}$.
يمكن تمثيل تكلفة البناء لكل قسم مستقيم كقيمة وظيفة $$$C_ {AB_ {i}}$، حيث يتم تحديد كل قطعة بشكل حدودي:

$$عرض $$ $ {\ displaystyle AB_i \ colon \ left \ {{\ start {محاذاة & s = s \ left (t \ right) - \ mbox {معلمة منحنى} ، \\ & h = h \ left (s (t ) \ right) - \ mbox {function of ارتفاع الارتفاع} ، \\ & c = c \ left (s (t) \ right) - \ mbox {وظيفة تكلفة وحدة البناء عند نقطة} ، \\ \ end {محاذاة}} \ اليمين .} $$ عرض $$

اين $$$t \ in \ left [0 ، 1 \ right]$- معلمة القطاع.

$$$C_ {AB_i} = \ int \ limit_ {AB_i} c \ left (s (t) \ right) \ sqrt {\ left [g_ {xy} (s (t)) + \ frac {\ جزئي h} {\ جزئية s_x} \ cdot \ frac {\ جزئية h} {\ جزئية s_y} \ right] \ dot {s} _ {x} \ dot {s} _ {y}} dt$اين $$$g$- الموتر المتري لسطح الأرض دون مراعاة التخفيف ، وهذا هو ، بعبارة بسيطة ، وظيفة قياس المسافة على سطح الأرض.

نظرًا لحقيقة أن كوكبنا له شكل جيودي ، فمن الضروري استخدام صيغ خاصة لقياس المسافات. لهذا نستخدم صيغة Haversinus. في ذلك ، يبدو شكل الكوكب وكأنه كرة ، ولكن هذا يكفي لأغراضنا ، لأن خطأ القياس يبلغ حوالي 0.3 ٪ ، وتبقى سرعة حساب المسافات بهذه الطريقة عالية.

نهج لإيجاد أفضل طريقة

ولكن قبل الانتقال إلى الانضمام إلى مجموعة من الكائنات ، تحتاج إلى معرفة كيفية العثور على المسار الأمثل بين الاثنين. طريقتان للقيام بذلك تتبادر إلى الذهن على الفور:

1. بناء رسم بياني ، ثم قم بتطبيق أقصر طرق البحث عن المسار ؛
2. استخدام حل يعتمد على أساليب التحسين.

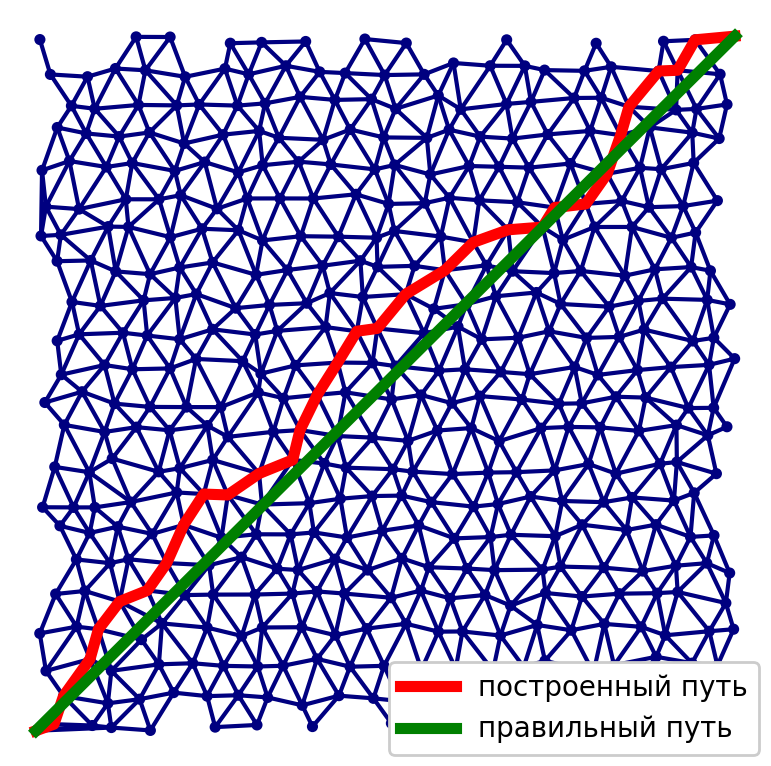
عند تنفيذ الطريقة الأولى ، لدينا مشكلة مرتبطة بطريقة إنشاء رسم بياني للحصول على أعلى دقة ممكنة من الحل. من الضروري إيجاد توازن بين عدد الرؤوس والحواف في الرسم البياني ، وجودة الحل ، والوقت اللازم لحسابه.

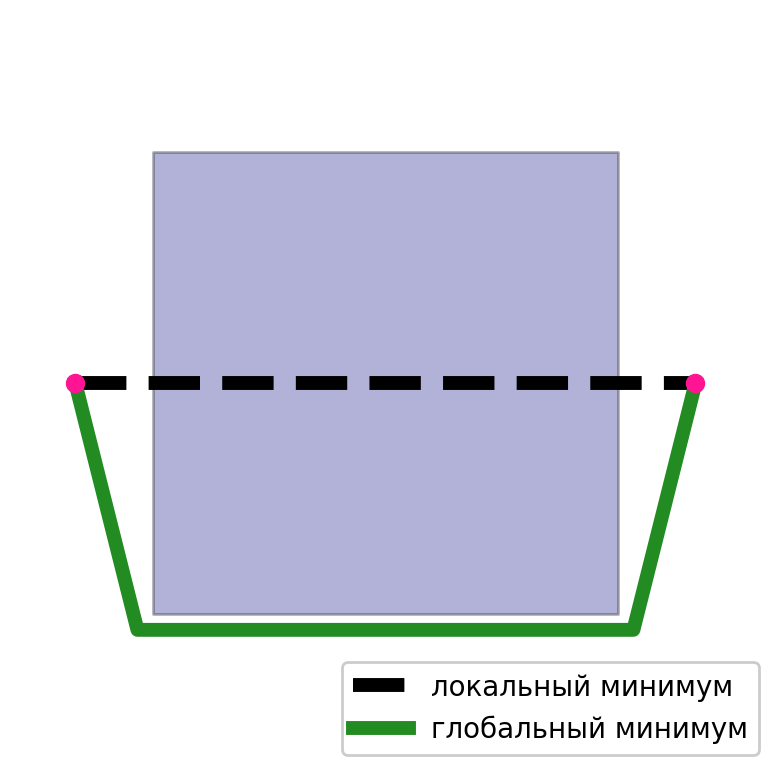
في الحالة الثانية ، المشكلة الرئيسية هي الحد الأدنى المحلي. من السهل اختيار حالة لا يتلاقى فيها الحل أو يكون بعيدًا عن الحل الأمثل. منذ الحل التي تم الحصول عليها بواسطة هذه الطريقة يعتمد بشكل لا يصدق على التقريب الأولي. إذا كان لدينا تقريب أولي جيد ، فستكون النتيجة عالية الجودة.

لذلك ، لدينا نهجين لحل هذه المشكلة. النوع الأول منخفض الجودة إلى حد ما ، لكن لا توجد مشكلة في الحجم المحلي الصغير. والثاني لديه مشكلة صغيرة المحلية ، ولكن حل ذات جودة عالية. وإذا قمت بدمج هذين النهجين بشكل صحيح ، فسوف تختفي عيوب كل منهما. نحن نأخذ الحل الذي تم الحصول عليه على الرسم البياني كتقريب أولي ، ثم نطبق طرق التحسين عليه.

في هذا الجزء من المقالة ، سننظر بالضبط في الحل المقترح لهذه المشكلة على الرسم البياني.

اختيار الأداة

لقد تم تحديد خطة عمل ، يبقى فقط "ترميزها". نظرًا لأننا في المرحلة الأولى من كتابة التطبيق ، كان لدينا القليل من المعرفة حول مجال الموضوع ، فقد احتجنا إلى لغة مرنة حتى يتسنى لك في حالة وجود بعض التقديرات المعمارية الخاطئة إعادة كتابة الكود بالكامل لبضع علب من البيرة المسائية. أردت أيضًا اختيار مكتبات لجميع المناسبات ، حتى لا ألجأ إلى اختراع الدراجات. لذلك ، تم اختيار بيثون كلغة برمجة رئيسية.

في التطبيق ، استخدمنا رصة تكنولوجية رائعة ، والتي لا تقتصر على ما يلي:

• رشيق للعمل مع البيانات الهندسية مثل المضلعات و polylines ؛
• geopandas للعمل مريحة مع رشيق .
• سكيبي لتخزين الرسم البياني المحسوب والعثور على أقصر الطرق على ذلك ، وكذلك العثور على الحد الأدنى من الأشجار الممتدة ؛
• PyTorch للعمل مع وظيفة التكلفة ؛
• وسادة للعمل مع الصور.

التنفيذ

يمكن تقسيم الوحدة إلى عدة مراحل:

• توليد وظيفة التكلفة ؛
• توليد الشبكة الحسابية.
• بناء الرسم البياني على أساس الشبكة ؛
• الرسم البياني الترجيح.
• حساب أقصر الطرق على الرسم البياني.

نظرًا لأن حواف الرسم البياني عبارة عن مقاطع ، يمكننا وزن هذه الحواف عن طريق حساب قيمة تكامل معين ، والذي تم تقديمه أعلاه. ولكن هناك العديد من الحواف في الرسم البياني ، وبالتالي ، يجب الحصول على قيم التكاليف والارتفاعات لعدد كبير جدًا من النقاط ، والتي قد تستغرق الكثير من الوقت.

في البداية ، كانت الفكرة هي العثور على تكلفة وحدة البناء من خلال تحديد ما إذا كانت النقطة تنتمي إلى مضلع أم لا. لكن تمت ملاحظة هذه الفكرة بسبب التعقيد الخوارزمي العالي لهذا النهج ، حيث يمكن أن يكون هناك العديد من المضلعات ، ولكل منها عدد كبير من الرؤوس.

لذلك ، لحل هذه المشكلة ، يمكننا تمثيل جميع المضلعات التي لدينا في صورة ، والتي في شكل رياضي هو مصفوفة. وبالتالي ، يمكننا الحصول على تكلفة وحدة البناء في نقطة تتجاوز O (1) ، وبالتالي يمكننا الحصول على تكلفة بناء ضلع معين بدقة عالية.

نحن الآن على استعداد لبناء رسم بياني ، ولكن لا توجد طريقة صحيحة فريدة لإنشاءه للحصول على حلول عالية الدقة. من أجل إنشاء رسم بياني ، من الضروري إنشاء شبكة حسابية ، أي مجموعة من النقاط في المنطقة قيد النظر ، متصلة بالترتيب المقابل بواسطة شرائح تشكل وجوه الخلايا. يمكن تقسيم الشبكات إلى نوعين: منتظم وغير متساو.

يصف نموذج الشبكة الموحد إحداثيات النقاط الفردية ، بحيث تكون المسافة بين عقد الشبكة متماثلة. تظهر شبكة غير متساوية كمجموعة عشوائية من النقاط الفردية.

لن يؤدي استخدام شبكة موحدة دائمًا إلى الحصول على نتيجة عالية الجودة للعثور على أقصر مسار ، لذلك ، من الضروري اختبار هذه الطريقة على شبكة غير متساوية. الأكثر تنوعا هو شبكة الثلاثي.

تم إنشاء الشبكة عن طريق إدخال الضوضاء ذات معامل معين في شبكة مستطيلة موحدة ، ثم تطبيق نقاط التثليث Delaunay لهذه المجموعة من النقاط.

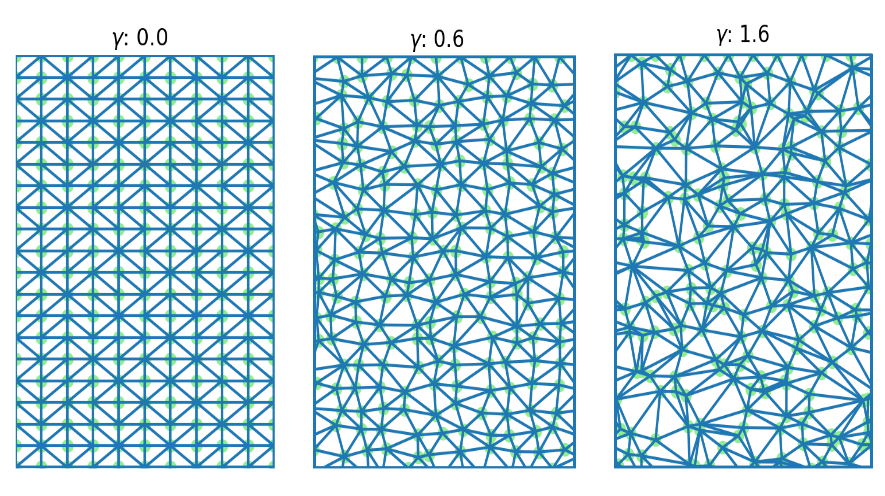
تم اختبار فعالية الشبكات المبنية على خرائط نموذجية مختلفة للمنطقة ، والتي أخذت في الاعتبار التكاليف المختلفة للمناطق والإغاثة ، ثم تم إجراء مقارنة مع الحل الذي تم الحصول عليه تحليليًا. من خلال البحث عن طول حافة الرسم البياني ومعامل إدخال الضوضاء في الشبكة الموحدة ، تم العثور على المعلمات المثلى لبناء المسار الأمثل بين نقطتين.

القضايا الرئيسية

في البداية سارت الأمور على ما يرام ، قامت الخوارزمية بحساب الشبكات المثلى ، ولكن بمجرد وجود مشكلة في جودة المسار المُنشأ. كانت الحالة بسيطة للغاية: كان عليك توصيل كائنين على خريطة طويلة إلى حد ما. لم ترغب الخوارزمية في بناء مسار كان صحيحًا بشكل واضح.

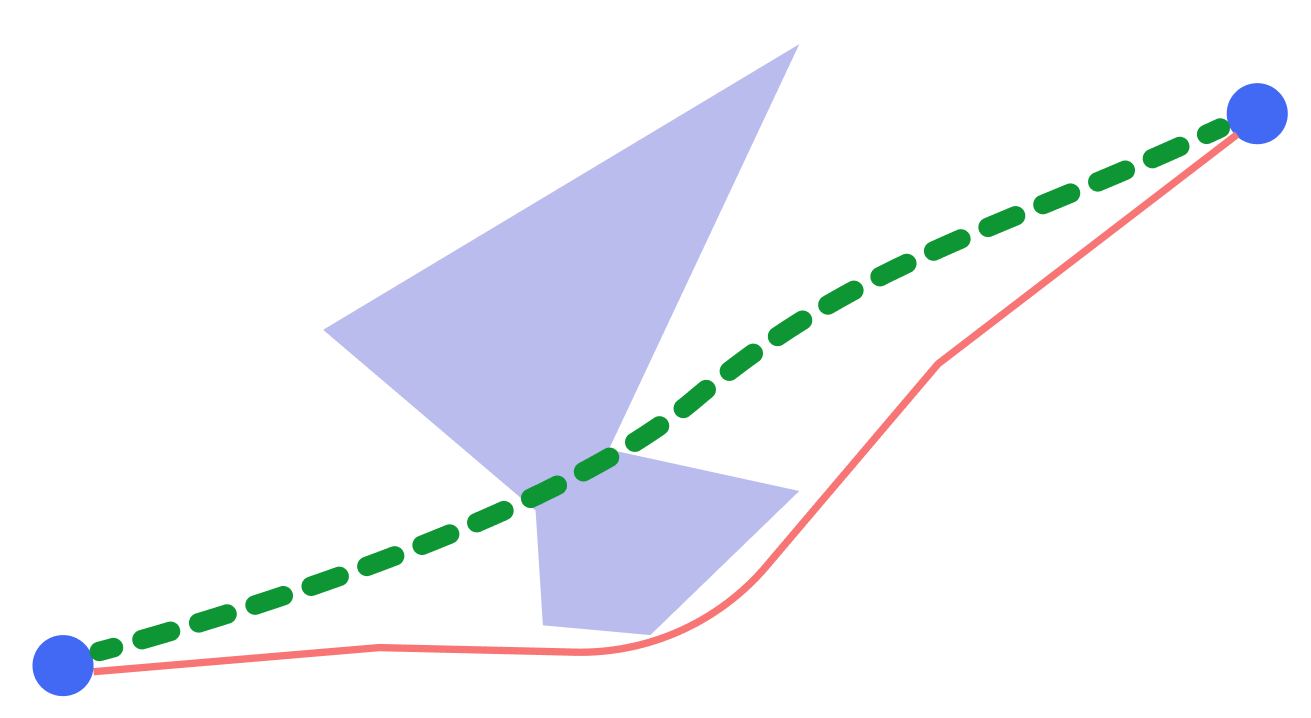
المشكلة ، كما هو الحال دائما ، كانت مع الشبكة الحسابية. واصلنا تجاربنا مع ظهور الشبكات وتوصلنا إلى استنتاج مفاده أن ربط القمم برسم بياني ، حيث يتم توصيل كل رأس بقرب جيران قريبين ، يعد حلاً لمشاكلنا.

الشبكات

بعد أن تعلمنا كيفية العثور على المسارات المثلى بين نقطتين ، كانت الخطوة التالية هي حل مشكلة إنشاء شبكة مثالية من الكائنات الخطية. الخوارزميات التي تمت مواجهتها في الأدبيات الخاصة ببناء أشجار شتاينر على الرسوم البيانية موجهة نحو مشاكل أكثر عمومية ، وبالتالي لن تكون فعالة في حالتنا. الرسم البياني الخاص بنا متناثر للغاية ، مع وجود عدد صغير من القمم الطرفية ، نسبة إلى إجمالي عدد القمم في الرسم البياني ، ويتم تطبيق مهمتنا أيضًا. لذلك ، لعدد من الأسباب الأخرى ، تقرر تطوير خوارزمية خاصة بنا تستخدم مجريات بحثية معينة لإنشاء شبكة مثالية بشكل فعال.

وصف الخوارزمية لإنشاء الشبكة المثلى على الرسم البياني لحالتنا هو موضوع لنشر منفصل ، ونحن لن تنظر فيه هنا. نظرًا لأنه عند حساب مهمة حقيقية ، من الضروري مراعاة العديد من الشروط الإضافية من صناعة البناء ذات الصلة بالمستخدم النهائي ، والتي تفرض قيودًا معينة على الخوارزمية المستخدمة.

حالة حقيقية

لذلك ، الآن ننتقل إلى نتائج الخوارزمية. مهمتنا هي توصيل مجموعة معينة من الكائنات بشبكة اتصال. حدثت مقارنة نتائج الخوارزمية مع شبكة طرق تم إنشاؤها مسبقًا. يبلغ الطول الإجمالي للشبكة الحالية 153.5 كم مقابل 122.6 كم للشبكة المحسوبة. وهذا يعطي حوالي 25 ٪ انخفاض في طول شبكة الطرق ، مما سيوفر في نهاية المطاف حوالي 5-15 ٪ على تكاليف بناء رأس المال.

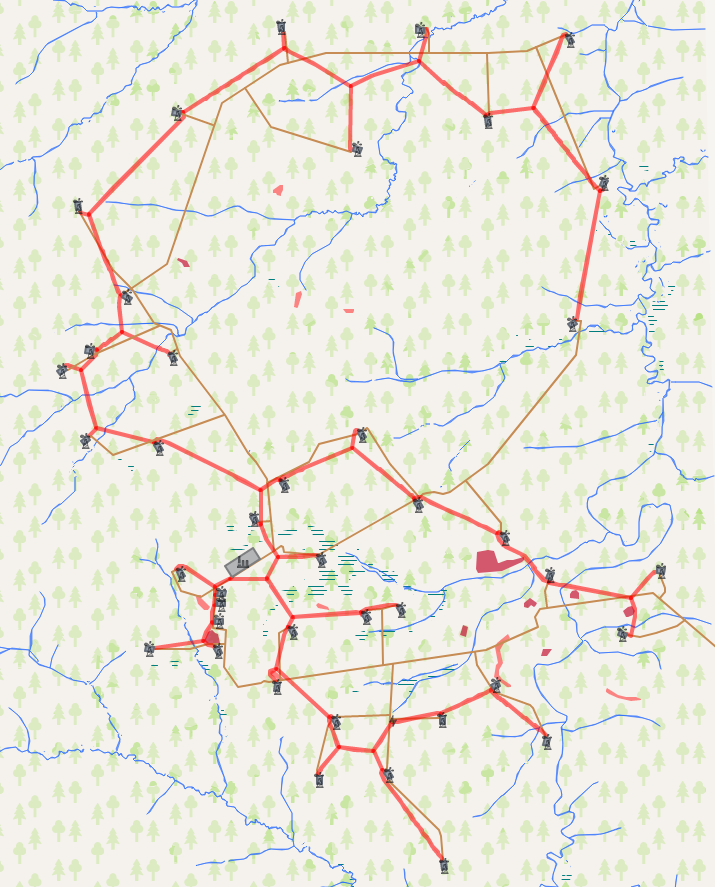
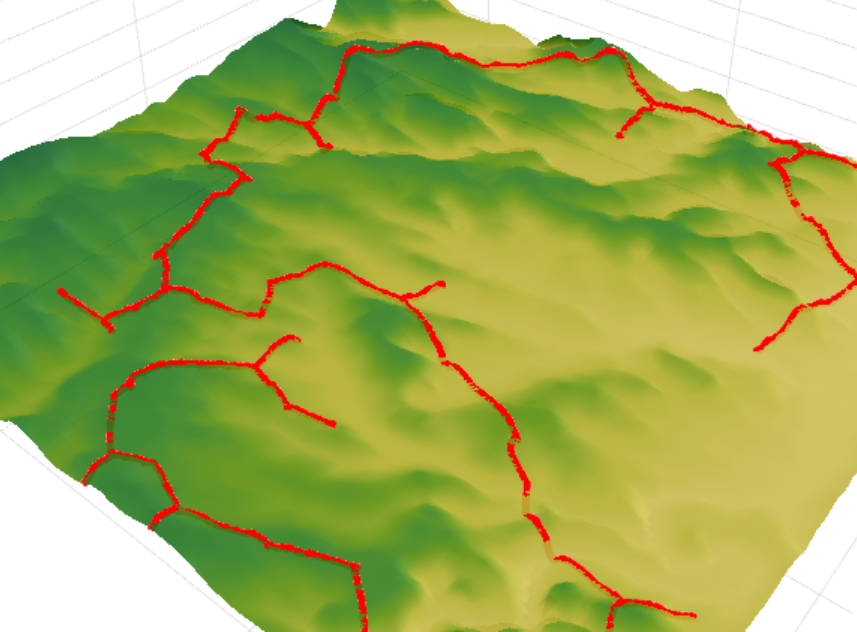
يمكنك الاطلاع عن كثب على نتائج الحسابات هنا .

سيكون وصف طرق التحسين المستخدمة في الجزء التالي من المقالة.