تاريخ Shipastik

المسامير في كل مكان

نحن نسميه Spikey ، وفي حياتي اليوم أقابله باستمرار:



إنه يأتي من كائن ثلاثي الأبعاد ، متعدد السطوح يسمى "المعيني الستين".



ولكن ما هو تاريخها ولماذا جعلناها رمزنا؟

أصل شوكة

في عام 1987 ، عندما كنا نعمل على تطوير الإصدار الأول من Mathematica ، كان أحد ابتكاراتها إمكانية إنشاء رسومات ثلاثية الأبعاد مستقلة عن الدقة تستند إلى أوصاف رمزية. في المظاهرات المبكرة ، سمح لنا ذلك بإنتاج صور واضحة بشكل مدهش لأشكال متعددة الوجوه العادية. ولكن مع اقتراب إصدار Mathematica 1.0 ، أردنا استخدام مثال أكثر إثارة للإعجاب. لذلك ، قررنا أن نأخذ آخر تعدد السطوح المنتظم - الإيكوساهيدرون - ونجعل منه شيئًا أكثر تعقيدًا من خلال إعطائه شكل نجمة ، أو بشكل أكثر تراكمًا بشكل صحيح. نعم ، هذا ما كانت عليه واجهة الكمبيوتر المحمول الأولى منذ 30 عامًا.



في البداية كانت مجرد مظاهرة لطيفة عملت بسرعة كبيرة على أجهزة الكمبيوتر الخاصة بنا في ذلك الوقت. ولكن سرعان ما بدأ استخدام الكائن الثلاثي الأبعاد الذي تم إنشاؤه كشعار لـ Mathematica. وبحلول الوقت الذي تم فيه إصدار الإصدار 1.0 في عام 1988 ، كانت إيكوساهيدرون النجمية في كل مكان:



مع مرور الوقت ، بدأت تظهر الإهداءات المختلفة للعديد من السطوح النجمية - مصنوعة بمواد وأحجام مختلفة:



ولكن بعد عام واحد فقط من إصدار Mathematica 1.0 ، كنا على استعداد لإصدار Mathematica 1.2 ، ولتقديم تعقيد المنتج ، كنا بحاجة إلى شعار متطور. دافع إيغور ريفين ، أحد مطورينا ، عن أطروحته الدكتوراه حول تعدد الوجوه في الفضاء الزائدي - وبفضل جهوده ، تم تزيين المواد الخاصة بالإصدار 1.2 بجهاز إيكوساهيدرون زائدي:



قدم لي الموظفون قميصًا مع شركة Shipastik الحديثة آنذاك بمناسبة عيد ميلادي الثلاثين عام 1989 ، وأقتبس أنني أؤيده حتى بعد سنوات عديدة:


"الشركة ممتعة"

بعد إصدار Mathematica 1.2 ، في موادنا التسويقية ، يمكن للمرء أن يجد مجموعة كاملة من متعدد الوجوه العادية الزائدية ، ولكن مع ظهور الإصدار 2.0 في عام 1991 ، قررنا أننا أحببنا إيكوساهيدرون الزائدي أكثر:



لكننا واصلنا استكشاف أشكال أخرى ارتفعت. مستوحاة من رسم ليوناردو دافنشي "نموذجًا خشبيًا" للإيكوساهيدرون النجمية (المصنوع بمنظور دقيق بشكل مدهش) لكتاب Luke Pacioli "On Divine Proportion" ، طلبنا إصدارًا 2.0 ملصقًا حيث يتم ترتيب خمسة رباعيات متقاطعة تتقاطع بحيث تكون رؤوسها الخارجية مكونة من dodecahedron:



اليوم ، من خلال الاطلاع على أرشيفي من عام 1991 ، أجد الكود "التوضيحي" ، ومن الجيد أن نرى أنه يمكن تنفيذه بسهولة في أحدث إصدار من Wolfram Language (على الرغم من أنه يمكن كتابته اليوم بشكل أكثر أناقة):



على مر السنين ، أصبح هذا طقوسًا غريبًا - استعدادًا لإطلاق الإصدار الرئيسي التالي من Mathematica ، سننظم اجتماعات جادة حيث نشارك في "اختيار Shipastik جديد". في بعض الأحيان يتعين عليك الاختيار من بين مئات الخيارات المختلفة التي تم إنشاؤها باستخدام خوارزميات مختلفة تمامًا:



ولكن على الرغم من أن لوحات الألوان تتغير ، وغالبًا ما تعكس Shipastiks وجود ميزات جديدة في النظام (وإن كان ذلك ضمنيًا إلى حد ما) ، فنحن لدينا تقليد مدته 30 عامًا يتمثل في اختيار خيارات ل dodecahedron الزائدي:



في الآونة الأخيرة ، أصبح من المعتاد دراسة الفضاء حدودي - على الرغم من أننا الآن تراكمت بالفعل مئات المعلمات:



يحتوي dodecahedron الزائدي على 20 قمة - كان مثالياً للاحتفال بالذكرى السنوية العشرين ل Mathematica في عام 2008. ولكن عندما أردنا أن نفعل شيئًا مماثلاً للاحتفال بالذكرى 25 في عام 2013 ، واجهنا مشكلة عدم وجود تعدد الوجوه العادية مع 25 رأسًا. لكن (في الواقع ، باستخدام وظيفة SpherePoints [25]) ، تمكنا من إنشاء رقم تقريبي ، وطباعته على طابعة ثلاثية الأبعاد لجميع موظفي الشركة ، بأحجام تتناسب مع مدة خدمة الموظفين.

خروج ولفرام | ألفا

في عام 2009 ، كنا نستعد لإصدار Wolfram | Alpha ، وكان النظام بحاجة إلى شعار. كان هناك العديد من المفاهيم:



أردنا التأكيد على أن Wolfram | Alpha يعمل عن طريق الحسابات ، وليس ، على سبيل المثال ، كمحرك بحث. ولبعض الوقت أردنا استخدام شيء مع التروس. لكننا أردنا أيضًا أن يشبه الشعار شعار Mathematica الطويل. وأدى ذلك إلى واحد من تلك المشاريع مثل "جنرأ الجنرال لدينا": إنشاء آلية العتاد من أشكال ارتفعت.

ساعدنا مستخدمًا قديمًا في Mathematica و Wolfram Language ، وهو مهندس ميكانيكي من المجر ، Sandor Kabai ، من خلال اقتراح "التروس المسننة":



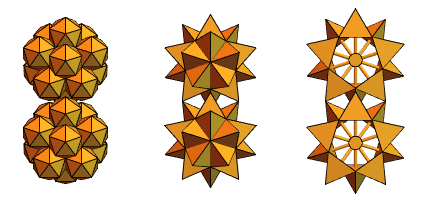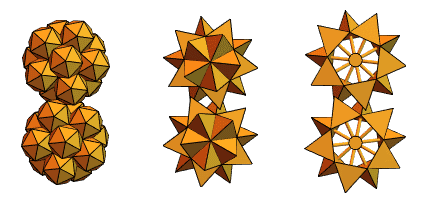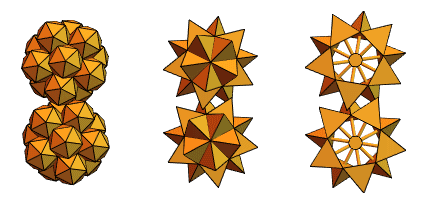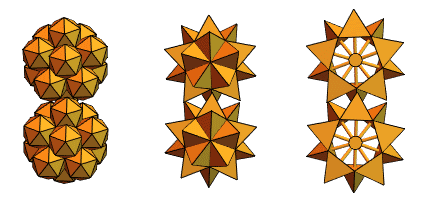
بالرجوع إلى رباعي السطوح المتقاطعة من الإصدار 2 ، قام بإنشاء شيء مثل هذا:



في عام 2009 ، أصبحت الطابعات ثلاثية الأبعاد شائعة للغاية ، واعتقدنا أنه سيكون من الجيد إنشاء شعار لـ Wolfram | Alpha يمكن طباعته. لم يكن الشكل المتعدد السطوح مناسبًا - فقد تنفجر المسامير وتشكل تهديدًا. الأشكال مثل المسامير من الإصدار 4 ، مع "المسامير آمنة" ، تفتقر إلى الأناقة.

لفترة من الوقت تشبثنا بفكرة مع التروس. لكن في النهاية ، قرروا أن الأمر يستحق إلقاء نظرة أخرى على المجسمات المتعددة السطوح العادية. ولكن أي متعدد السطوح يمكن أن نختار؟

بالطبع ، هناك عدد لا حصر له من متعدد الوجوه ممكن. لكن بالنسبة لشعارنا ، أردنا اختيار متعدد السطوح "متماثل" وإلى حد ما "صحيح". يمكن اعتبار خمسة أشكال متعددة الوجوه العادية (أو "المواد الصلبة الأفلاطونية") - التي تكون وجوهها هي نفس المضلعات العادية - "الأكثر انتظامًا" على الإطلاق:



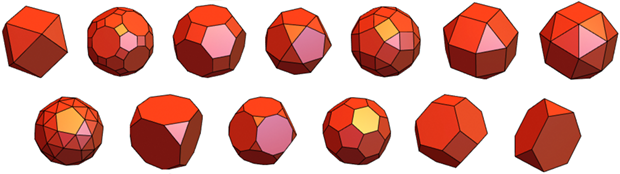
هناك 13 جثة أرخميدية أخرى - لها رؤوس متماثلة ، والمضلعات المنتظمة ، على الرغم من أنواع مختلفة ، تعمل كوجوه:



هناك العديد من أنواع "صحة" متعدد الوجوه. ومن الأمثلة على ذلك "تعدد الوجوه المتجانسة" الذي يظهره ملصق من مجلة Mathematica Journal منذ عام 1993:



على مر السنين التي جمعها إريك وينشتاين ، والتي تحولت بحلول عام 1999 إلى MathWorld ، حاول تضمين مقالات عن أكبر عدد ممكن من المضلعات. في عام 2006 ، كجزء من إدراج بيانات منظمة منتظمة في Mathematica و Wolfram Language ، بدأنا في تضمين بيانات المضلع مع MathWorld. نتيجة لذلك ، بعد إصدار الإصدار 6.0 في عام 2007 ، ظهرت وظيفة PolyhedronData فيه ، والتي تضمنت بيانات شاملة عن 187 مضلّعًا ملحوظًا:



في Mathematica و Wolfram Language ، يمكنك دائمًا إنشاء مضلعات منتظمة ، ولكن أصبح من السهل الآن القيام بذلك. مع الإصدار 6.0 ، أصدرنا أيضًا مشروع مظاهرات Wolfram ، الذي سرعان ما بدأ في التجديد بالعديد من العروض التوضيحية المتعلقة بالأشكال المتعددة الوجوه.

صُنعت واحدة منها بواسطة ابنتي كاترينا عندما كانت في العاشرة من عمرها (وهي اليوم تواصل تطويرها في مجالات الهندسة): هذه "متعددة السطوح" ، موزعة بواسطة جميع الأشكال المتعددة السطوح من PolyhedronData [] المستخدمة:



على هذه الخلفية ، أردنا في عام 2009 "اختيار متعدد السطوح" لـ Wolfram | Alpha. تم تحديد كل شيء يوم الجمعة ، 6 فبراير ، عندما بدأت العمل بمفردي.

لقد حافظت على هذا الكمبيوتر الدفتري ، وهذا يدل على أنني حاولت أولاً تنفيذ الفكرة المشكوك فيها المتمثلة في وضع كرات في قمم متعدد الوجوه:



ولكن ، كما تم تسجيله في " سجل الحواسب المحمولة" ، بعد دقيقتين فقط ، قمت بالتبديل إلى روابط متعددة السطوح - كانت جميعها برتقالية ، ثم أردنا استخدامها للشعار:





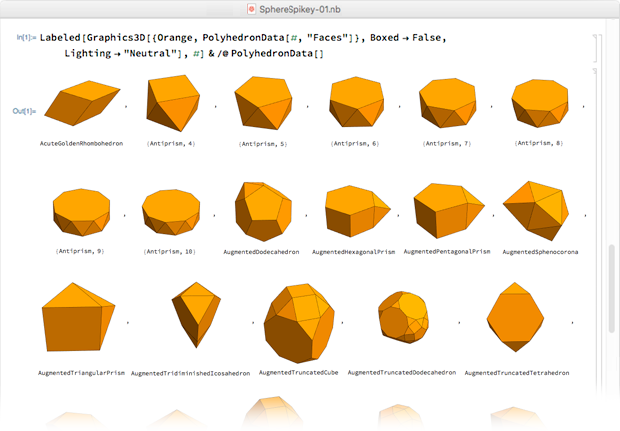
تم ترتيب تعدد الوجوه حسب الترتيب الأبجدي بالاسم ، وفي السطر الثامن والعشرين ظهر - سداسي الشكل المعيني.



بعد دقيقتين ، في الساعة 00:24:24 ، 7 فبراير 2009 ، اكتشفت هذا الشكل السداسي الشكل المعيني وحوله إلى وضع متماثل ، نستخدمه الآن:



أردت أن أرى كيف سيبدو باللون الرمادي وفي صورة ظلية ، وبعد أربع دقائق استخدمت ColorSeparate لمعرفة:



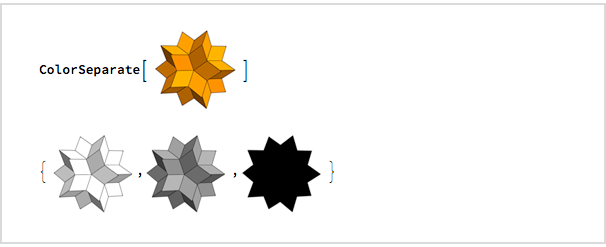
بدأت على الفور في كتابة رسالة بريد إلكتروني أرسلتها في الساعة 00:32:

أنا حقا أحب RhombicHexecontahedron. لديها شكل مثير للاهتمام ومتناظر للغاية. يبدو لي أن دقتها تناسبنا تمامًا وأن الصورة الظلية تبدو معقولة جدًا.



من الواضح ، لقد قمت فقط بنسخ RhombicHexecontahedron من دفتر الملاحظات (أشك في أنني قد كتبت السداسي [hexecontahedron] دون أخطاء). من أرشيفي ، أعلم أن هذه كانت المرة الأولى التي أكتب فيها اسم المجسم متعدد السطوح ، والذي أصبح مفضلاً ليصبح المفضل لدي.

في Wolfram Language ، كان من السهل جدًا الحصول على صورة لسداسي الشكل المعيني ، واللعب بها:



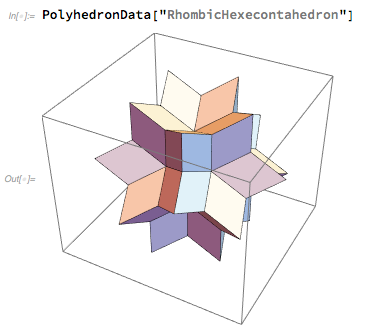
بحلول يوم الاثنين ، كان من الواضح أن سداسية الشكل المعينية قد فازت - وكان قسمنا البصري مشغولاً في وضعه كشعار لـ Wolfram | Alpha. جربنا توجهات مختلفة منه ، لكن في النهاية استقرنا على الموقف المتماثل "في مرأى ومسمع" الذي اخترته. (نحتاج أيضًا إلى اختيار أفضل "البعد البؤري" للزاوية الأكثر ملائمة).



مثل إيكوساهيدرون المرقط من الإصدار 1.0 ، يحتوي سداسي الوجوه المعيني على 60 وجهًا. لكن بطريقة ما ، بفضل مجموعات "خمس بتلات" ، تبدو أكثر أناقة. تم بذل الكثير من الجهد في اختيار مثل هذا التظليل للوجوه بحيث يعكس الرسم ثنائي الأبعاد الكائن ثلاثي الأبعاد بشكل صحيح. ولكن سرعان ما قدمنا ​​النسخة الرسمية الأولى من شعارنا:



سرعان ما بدأت تظهر في كل مكان ، وكتحية لأفكارنا المبكرة ، غالبًا على خلفية مزينة بتروس:



بعد بضع سنوات ، صححنا قليلاً تظليل الحواف ، مما أدى إلى إنشاء شعار Wolfram | Alpha ، والذي لا يزال قيد الاستخدام:



مسدس المعينية

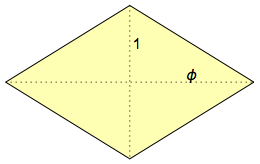
ما هو سداسي الشكل المعيني؟ في اللغة الإنجليزية ، يطلق عليه hexecontahedron ، لأنه يحتوي على 60 وجهًا ، و ἑξηκοντα (hexekont) هي الكلمة اليونانية لـ "60". وجوهها هي المعين الذهبي ، والتي سميت بذلك لأن أقطارها مرتبطة ببعضها البعض وفقًا للنسبة الذهبية: φ = (1 + √5) / 2 & sime؛ 1،618:



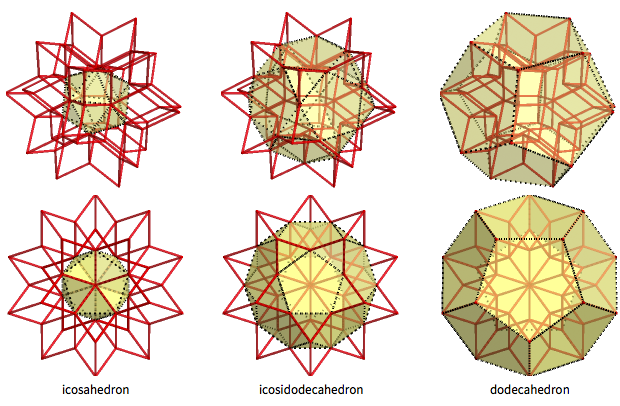
السداسية المعينية عبارة عن جسم وسيط مثير للاهتمام بين الإيكوساهيدرون والديكوداهيدرون (مع الإيكودوكاهيدرون بينهما). تشكل القمم الداخلية ذات الشكل المعياري 12 رأسًا سداسيًا الشكل ، كما تشكل القمم الخارجية العشرون رأسًا عاديًا. 30 "القمم الوسيطة" تشكل الإيكودوديكهرون ، ذو 32 وجهًا (لها 20 وجهًا ثلاثي الأضلاع و 12 وجهًا خماسيًا):



في المجموع ، يحتوي سداسي الشكل المعيني على 62 رأسًا و 120 حافة (بالإضافة إلى 120-62 + 2 = 60 وجهًا). له ثلاثة أنواع من القمم ("داخلية" و "متوسطة" و "خارجية") ، تقابل 12 + 30 + 20 رأسًا من المجسم الإيكوساهيدروني ، والإيكودودكاهيدرون والوديكاهيدرون. في هذه القمم 3 و 4 و 5 حواف تتلاقى معا ، على التوالي. لكل وجه قمة واحدة "داخلية" تلتقي عندها 5 حواف ، وقمة خارجية واحدة تلتقي فيها ثلاثة حواف ، واثنتان من العقد "المتوسطة" حيث تلتقي 4 حواف. القمم الخارجية والداخلية هي القمم ذات الزوايا الحادة للقوافي الذهبية ، والقوس الوسيطة ذات الزوايا المنحرفة.

الزاوية عند قمم مدببة من المعين الذهبي هي 2 تان ⁻¹ (φ ⁻¹ ) ≈ 63.43 درجة ، وعند قمم مدببة حادة 2 تان ⁻¹ (φ) .57 116.57 درجة. تسمح لك هذه الزوايا بتجميع سداسية الشكل المعينية من مُنشئ Zometool باستخدام الدعامات الحمراء فقط (كما في حالة dodecahedron):



من بين 120 من حواف سداسية الشكل المعينية لـ 60 "مفصلات داخلية" ، تكون الزاوية ثنائية السطوع 4π / 5 = 144 ° ، وفي 60 منها خارجية تبلغ 2 is / 5 = 72 °. الزوايا المتعاقد عليها من القمم الخارجية والداخلية هي π / 5 و 3π / 5.

لرسم سداسي الشكل المعيني ، تحتاج إلى معرفة الإحداثيات ثلاثية الأبعاد لرؤوسها. يتم الحصول عليها بسهولة باستخدام حقيقة أن سداسي الشكل المعيني ثابت بالنسبة لمجموعة الايكوساهيدرون ، بحيث يمكنك البدء مع المعين الذهبي واضافة 60 مصفوفة تشكل تمثيل ثلاثي الأبعاد لمجموعة الايكوساهيدرون. هذا ، على سبيل المثال ، يعطي الإحداثيات النهائية للرؤوس في {± φ ، ± 1،0} ، {± 1 ، ± φ ، ± (1 + φ)} ، {± 2φ ، 0،0} ، {± φ ، ± ( 1 + 2φ) ، 0} ، {± (1 + φ) ، ± (1 + φ) ، ± (1 + φ)} والتباديل الدوري مع كل العلامات الممكنة.

بالإضافة إلى حقيقة أن وجوه سداسي الشكل المعيني هي المعين الذهبي ، يمكن بناء سداسي الشكل المعيني من 20 المعين الذهبي (حيث تكون الوجوه الستة المعينية الذهبية):



هناك طرق أخرى لإنشاء سداسي الشكل المعيني من متعددات الوجوه الأخرى. يمكن الحصول عليها من خمسة مكعبات متقاطعة ومن 182 dodecahedrons في اتصال مع الوجوه:



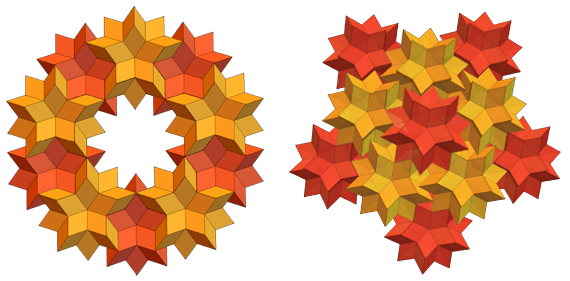
لا يمكنك وضع فسيفساء مستمرة من المعين الستين مسدس الشكل ، لكنها تتشابك بشكل جيد مع بعضها البعض (ونعم ، رأيت عشرات من الورق Shipastiks قابلة للطي بهذه الطريقة):



يمكنك أيضًا إنشاء جميع أنواع الخواتم وتكوينات أخرى منها:



قريب من سداسية المعينية (جمهورية صربسكا) هو المعين ثلاثين رباعي الاسطح (RT). RS و RT لها وجوه التي هي المعين الذهبي. لكن RS لديه 60 منهم ، و RT لديه 30. إليك ما يبدو عليه RT منفصل:



يتم استثمار العديد من RTs في جيوب RS ، وتتحول الأشياء المماثلة إلى:



Sandor Kabay ، التي ذكرناها سابقًا ، أصبحت مهتمة بـ RSh و RT حوالي عام 2002. وبعد إطلاق مشروع مظاهرات Wolfram ، أضاف هو ، إلى جانب عالم الرياضيات السلوفيني إيسيدور هافنر ، أكثر من مائة عرض توضيحي للمشروع المتعلق ب RS و RT والعديد من ممتلكاتهم:

نماذج ورقة شائك

بمجرد أن قررنا أن Shipastik سيكون RS ، بدأنا في صنع نماذج 3D. الآن أصبح من السهل جدًا القيام بذلك باستخدام وظيفة Printout3D [PolyhedronData [...]] ، ويمكن العثور على الطرز المحسوبة بالفعل على موارد الجهة الخارجية .

في مايو 2009 ، عندما تم إطلاق Wolfram | Alpha ، كان لدينا بالفعل العديد من المسامير ثلاثية الأبعاد في متناول اليد:



ولكن ، مع الاستعداد لموسم العطلات الأول بعد هذا الحدث ، قررنا أن نمنح الجميع الفرصة لإنشاء شباكستك ثلاثية الأبعاد الخاصة بهم. أولاً ، نظرنا في الخيار مع 20 مغنطيسًا مؤلفًا من البلاستيك المغلف بالبلاستيك. لكنها خرجت باهظة الثمن ، ولم تلتصق ببعضها البعض جيدًا.

هذا قادنا إلى فكرة جعل Shipastik من الورق أو الورق المقوى الرقيق. لذلك ، في البداية أردنا وضع مخطط يمكن طيه في Shipastika:



عملت ابنتي كاترينا كاختبار (وما زالت لديها عينة اختبار) ، لكن أصبح من الواضح أن الكثير من المواقف غير المريحة تظهر في عملية الطي ، حيث من غير الواضح كيفية الانتقال من موضع إلى آخر. يمكنك عمل عدد كبير من التصميمات (يوجد 43،380 منها فقط للديكيديهدرون والإيكوساهيدرون) - واعتقدنا أنه ربما سيكون من الممكن اختيار شيء أفضل منها:



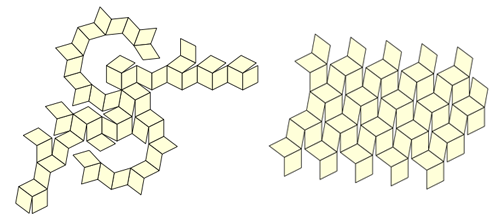
ولكن ، عندما لم نتمكن من العثور على مثل هذا المخطط ، كانت لدينا فكرة جديدة (وإن كانت واضحة): إذا كان النموذج سيُمسك بالأذنين ، فلماذا لا نجعله من عدة قطع؟ لقد أدركنا بسرعة أنك تحتاج إلى أن تأخذ فقط 12 قطعة متطابقة من هذا النوع:



بمساعدتهم ، أنشأنا " مجموعات للتماثيل الورقية ":



كانت مهمة مثيرة للاهتمام كتابة التعليمات التي كان من السهل فهمها ، ولكن بعد عدة تكرارات ، أصبحت التعليمات متطورة وبسيطة:



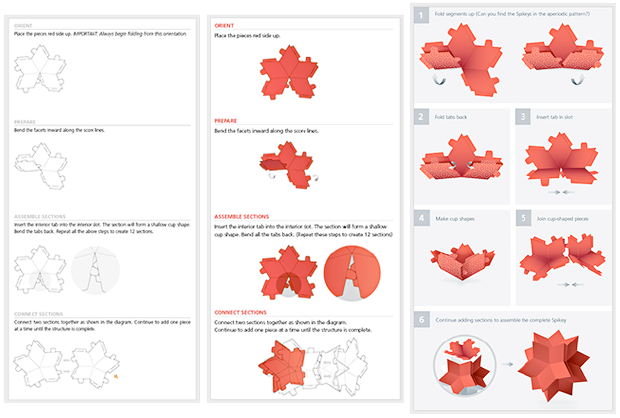
وبعد أن ذهبت ورقة Shipastiks إلى الناس ، بدأ مستخدمونا في إرسال جميع أنواع صور Shipastik إلينا "على الأرض":

الطريق إلى مسدس المعينية

المكعب متعدد الجوانب من مصر القديمة

من غير المعروف من الذي وصف لأول مرة المواد الصلبة الأفلاطونية. ربما تم ذلك بواسطة فيثاغورس (الذين عاشوا بالقرب من هذه الرواسب الكبيرة من بلورات البايرايت متعددة الأوجه). ربما فعل شخص ما هذا قبلهم بفترة طويلة. ربما كان معاصرا لأفلاطون ، تيتيت أثينا . ولكن ، على أي حال ، بحلول زمن أفلاطون (حوالي 400 قبل الميلاد) ، كانت هناك خمس مواد صلبة أفلاطونية معروفة. وعندما كتب إقليدس عناصره (حوالي 300 غرام قبل الميلاد) ، كانت إحدى دعائم هذا العمل دليلًا على عدم وجود تعدد الوجوه العادية الأخرى. هذا الدليل معروف بأخذ أكبر عدد من الخطوات من البديهيات الإقليدية الأصلية - 32.

واستخدمت المواد الصلبة الأفلاطونية للنرد والزينة. لكن تم تكليفه أيضًا بدور مركزي في التفكير في الطبيعة - على سبيل المثال ، اقترح أفلاطون أن كل شيء يمكن أن يتكون منهم: الأرض من المكعبات ، والهواء من أوكتاهيدرونات ، والماء من إيكوساهيدرون ، والنار من رباعي الأسطح ، والسماء ("الأثير") ) من dodecahedrons.

ماذا عن المجسمات المتعددة الأخرى؟ في القرن الرابع الميلادي كتب باب الإسكندرية أنه قبل قرنين من الزمان اكتشف أرخميدس 13 "تعدد الوجوه العادية" - على ما يبدو ، ما يسمى الآن الأجسام الأرخميدية - على الرغم من أن تفاصيل هذا ضاعت. ولمدة ألف عام ، لم يحدث سوى القليل في تعدد الوجوه. ولكن في القرن الخامس عشر ، مع بداية عصر النهضة ، أصبحت المجسمات المتعددة الأبعاد فجأة عصرية مرة أخرى. استخدمهم ليوناردو دا فينشي وألبرشت دورر بانتظام في الفن والتصميم ، حيث اكتشفوا بعض الأجسام الأرتشميدية - بالإضافة إلى اكتشاف تعدد الوجوه الجديد ، على سبيل المثال ، الإيكودودكاهيدرون.

لكن أكبر خطوة للأمام في تعدد الوجوه كان عمل يوهانس كبلر في بداية القرن السابع عشر. بدأ كل شيء بنظرية أنيقة ، وإن كانت غير صحيحة تمامًا. يعتقد كبلر ، بناءً على الافتراضات اللاهوتية ، أنه ينبغي إنشاء الكون بدقة رياضية ، واقترح أن تتحرك الكواكب الستة المعروفة في ذلك الوقت على طول مجالات متداخلة مدرجة ووصفت حول خمس مواد صلبة أفلاطونية:



في كتابه الصادر عام 1619 ، هارمونيسيس موندي ، هارموني أوف ذا وورلد ، جادل كيبلر بأن العديد من ميزات الموسيقى والكواكب والأرواح تعمل وفقًا للعلاقات والمبادئ الهندسية المماثلة. لتأكيد الحجج ، درس كيبلر المضلعات ومتعددة الوجوه ، خاصة مع الاهتمام بالأشياء التي تشكل مجموعات كاملة ، مثل المواد الصلبة الأفلاطونية.

لقد درس "تعدد الوجوه الملامسة" الذي تمهد به الطائرة - ووجد ، على سبيل المثال ، " بلاطات وحشية " ، كما سماها (يتكون من خماسيات ، خماسية وعشرات). قام بدراسة "تعدد السطوح النحاسية" ووجد العديد من الإصدارات النجمية من المواد الصلبة الأفلاطونية ( وجسم كبلر - بونسوت ). في عام 1611 ، نشر كتابًا صغيرًا يتعلق بالهيكل السداسي لرقائق الثلج ، كُتب كهدية للعام الجديد لأحد رواده. في هذا الكتاب ، ناقش التعبئة ثلاثية الأبعاد للكرات (والذرات الكروية) ، مقترحًا فرضية أن التعبئة الأكثر كثافة للكرات في الفضاء ثلاثي الأبعاد (نلاحظ بانتظام تنفيذه في عبوات الفاكهة في المتاجر) هي عبوة مكعبة مركزية (تم إثبات هذه الفرضية رسميًا فقط بعد عام 2000) سنوات - باستخدام Mathematica).

في حزم Kepler المختلفة ، يتم إخفاء تعدد السطوح المختلفة. لنبدأ من أي مجال ، ونأخذ جيراننا وربط مراكزهم لجعل قمم متعدد السطوح. في أضيق عبوات كيبلر ، يلمس 12 آخرون أي كرة ، ومن مراكزهم يتم الحصول على كوبوكتاهدرون مع 12 رأسًا و 14 وجهًا. لكن كبلر وصف أيضًا حزمة أخرى ، أقل كثافة بنسبة 8٪ ، حيث تغطي كل كرة 8 كرات أخرى ، و 6 أخرى قريبة جدًا. إذا وصلنا مراكزهم ، فسوف نحصل على dodecahedron المعينية ، مع 14 رأسًا و 12 وجهًا:



بعد اكتشاف ذلك ، بدأ كيبلر في البحث عن "تعدد الوجوه المعينية" الأخرى. في الدودكاهيدرون المعيني الذي وجده ، تتكون المعينات من أزواج من مثلثات متساوية الأضلاع. ولكن بحلول عام 1619 ، درس كيبلر أيضًا المعين الذهبي - وعثر على المعيني من ثلاثين جانبًا ، وبعد ذلك رسم في كتابه صورته الجميلة ، بجانب الثنائي المعيني الشكل:



وجد Kepler على الفور طلبًا للمضلعات المعينية: أراد استخدامها ومكعبًا لبناء نموذج من الكرات المتداخلة المناسبة لمدار مدارات أقمار كوكب المشتري الأربعة التي اكتشفها غاليليو عام 1610.

لماذا لم يفتح كيبلر مسدس سداسي الشكل؟ أعتقد أنه اقترب منه. درس غير محدب النغمات المتعددة السطوح. نظر إلى تعدد الوجوه المعينية. ولكن ، على ما يبدو ، نظرياته الفلكية ، كان المعيني من جانب وثلاثين يكفي ، وبعد ذلك توقف عن البحث.

نتيجة لذلك ، بطبيعة الحال ، أصبحت قوانين كيبلر ، غير المتعلقة بالعديد السطوح ، هي المساهمة الرئيسية لعلم الفلك الذي نجا منها. لكن عمل كيبلر في مجال متعدد السطوح - وإن كان يتم في إطار نظرية فيزيائية غير صحيحة - لا يزال يمثل مساهمة أبدية في الرياضيات.

على مدى القرون الثلاثة التالية ، تم العثور على المزيد من المجسمات المتعددة للصحة المختلفة - وبحلول بداية العشرين ، عرف علماء الرياضيات بالفعل الكثير من أنواعها:



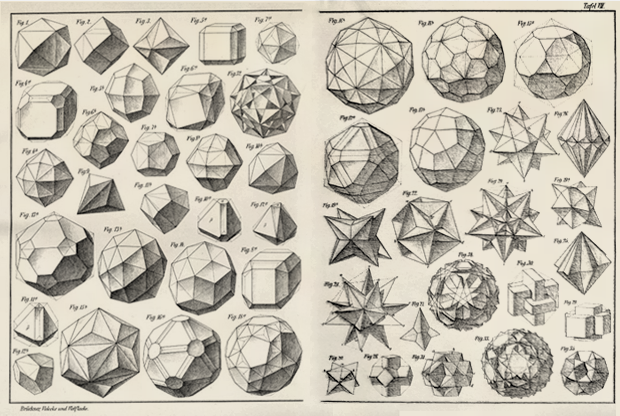
ولكن ، بقدر ما أستطيع أن أقول ، لم يكن هناك RS بينهم. كان اكتشافه ينتظر عمل هيلموت أونكلباخ . من مواليد عام 1910 ، دافع عن الدكتوراه في الرياضيات في جامعة ميونيخ في عام 1937 (على الرغم من أنه درس الفيزياء لأول مرة). وقد كتب العديد من الأعمال حول رسم الخرائط المطابقة ، وربما - بسبب دراسة رسم خرائط الأشكال المتعددة الوجوه - نشر في عام 1940 العمل المعنون "Edge-Symmetric Polyhedra" باللغة الألمانية.

وأوضح أن هدفه كان دراسة شاملة لجميع الأشكال المتعددة الوجوه الممكنة التي تفي بتعريف جديد خاص للصحة: ​​جميع الحواف لها نفس الطول وتكون في مستوى تناظر الأشكال المتعددة السطوح. كانت النتيجة الرئيسية للعمل جدول يحتوي على 20 صورة متعددة الأشكال لهذه الخاصية:


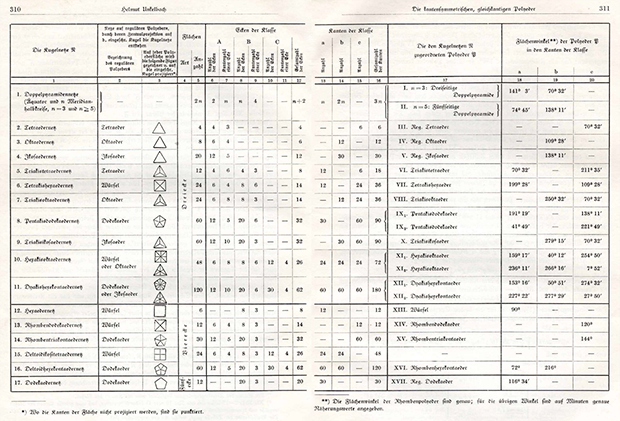قابل للنقر

معظمهم كانوا بالفعل الشهيرة. لكن Unkelbach خص بها ثلاثة منهم ، والتي اعتبرها جديدة: اثنان من hexaciscosahedra (أو disdakis dodecahedron) ، واثنين من hexacisicosahedra (أو disdacystriacontahedron) وما يسمى Rhombenhexekontaeder. واعتبر بوضوح أن RSh إنجازه الرئيسي ، وتضمن صورة لنموذجه الذي أدلى به بنفسه:



كيف أحضر RS؟ بدأ مع dodecahedron ، وحدد اثنين من الطائرة من التماثل:



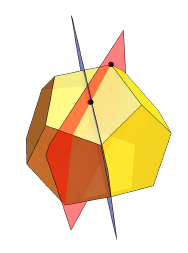
ثم قسّم كل وجه من وجوهه:



ثم ، في جوهره ، قام بالضغط على مراكز كل وجه من الوجوه بمسافة مساوية للمسافة المعتادة للمركز مضروبة في α معينة:



بالنسبة إلى α <1 ، لم تتقاطع الوجوه الناتجة. لكن بالنسبة لمعظم قيم α ، لم تكن جوانبها متساوية. يحدث هذا فقط في حالة معينة - عندما يتزامن متعدد السطوح الناتج تمامًا مع RS.

اعتبر Unkelbach عمله 1940 ليكون "الاحماء" لدراسة أكثر شمولا من "متعدد الوجوه متماثل" مع متطلبات التناظر أقل صرامة. لكن بالفعل ، بالطبع ، كانت معجزة أنه بعد بداية الحرب العالمية الثانية ، تم نشر مجلة رياضية في ألمانيا - بعد وقت قصير من هذا المنشور ، تم استدعاء Unkelbach إلى المقدمة ، حيث طور طوربيدات صوتية للأسطول الألماني لعدة سنوات.

لم ينشر المزيد من الأعمال على تعدد الوجوه ، وتوفي في عام 1968. بعد سنوات ، عاد إلى الخرائط المطابقة ، وبدأ أيضًا في نشره على نظرية التصويت ، معتبرًا أنه مفتاح إنشاء ديمقراطية تعمل جيدًا ، والتفكير في أن علماء الرياضيات ملزمون بجعل الناس بدأ استخدامه.

لكن ، حتى في أعمال 1940 ، يمكن أن تبقى RS هناك إلى الأبد إذا لم يكتب هارولد سكوت ماكدونالد كوكسيتر في عام 1946 مراجعة قصيرة لهذا العمل لمجلة American Mathematical Reviews الجديدة نسبيًا. يسرد مراجعته المجسمات المتعددة الوجوه المذكورة في العمل ، حيث يستطيع عالم الطبيعة سرد الأنواع الجديدة التي اكتشفها في رحلة استكشافية. الشيء الرئيسي هو أنه وصف هناك "سداسية الشكل المعينية الرائعة" ، وذكر أن "شكل وجوهها يتزامن مع شكل وجوه من جانب الثلاثين ، والتي يتم الحصول عليها من خلال إعطاء شكل نجمة".

لم تكن Polyhedrons موضوعًا شائعًا في الرياضيات في منتصف القرن العشرين ، ولكن كان Coxeter هو الداعم الرئيسي له - وكان مرتبطًا بشكل ما بكل من درسها. في عام 1948 ، نشر كتاب "العلماء السياسيون الصحيحون". إنه يصف بشكل منهجي العديد من العائلات متعددة السطوح المنتظمة ، على وجه الخصوص ، والنغمة المتعددة السطوح الكبيرة الثلاثية - في الواقع ، تحتوي على RS:



لكن في كتابه ، لا يذكر Coxeter بشكل مباشر RS ، وعلى الرغم من أنه تم تكريمه بمراجع بعض عشاق متعدد الوجوه ، إلا أن RS ظل غير معروف.

البلورات

لطالما كانت البلورات أمثلة مهمة على تعدد الوجوه في الطبيعة. ولكن بحلول القرن التاسع عشر ، عندما اكتسبت النظرية الذرية المزيد والمزيد من الاعتراف ، بدأ العلماء في إجراء المزيد من البحوث الجادة في مجال علم البلورات وترتيب الذرات في البلورات. بدأ تعدد الوجوه في الظهور بشكل متكرر ، على وجه الخصوص ، في تمثيلات هندسية لتكرار كتل الذرات ("الخلايا") في البلورات.

بحلول عام 1850 ، كان من المعروف أنه لا يمكن أن يكون هناك سوى 14 من هذه الأشكال الهندسية - من بينها هناك أيضا واحدة على أساس dodecahedron المعينية. وهي ملحوظة لوجود تماثلات من الدرجة الثانية أو الثالثة أو الرابعة أو السادسة - والتي ، في جوهرها ، هي نتيجة لحقيقة أنه لا يمكن ملء الفضاء إلا بأشكال متعددة الوجوه ، تمامًا مثل المضلعات النظامية فقط مثل المربعات يمكنها ملء طائرة ثنائية الأبعاد ، المثلثات والسداسي.

ماذا عن المواد الأخرى غير البلورية - مثل السوائل أو الزجاج؟ منذ بداية القرن العشرين ، اهتم الناس بإمكانية وجود تماثل تقريبي من الدرجة الخامسة على الأقل هناك. لن يكون من الممكن ملء المساحة باستخدام الرموز المجسمة الصحيحة ، لكن قد يكون من الممكن إنشاء أقسام ذات عشرين وجهًا مع وجود فجوات صغيرة بينها.

بقي هذا السؤال دون حل حتى الثمانينيات ، عندما أثبتت دراسة بلورات حيود الإلكترون باستخدام سبيكة مبردة بسرعة من الألمنيوم والمنغنيز وجود تماثل خمسة أضعاف. نظريات لتحقيق هذا التناظر موجودة بالفعل ، وبعد بضع سنوات ، ظهرت أيضًا صور من مجهر إلكتروني ، والتي ظهرت عليها جسيمات لها شكل معيني من ثلاثين جانبًا:



وبينما تخيل الناس كيف يمكن الجمع بين هذه heptahedrons الثلاثين مع بعضها البعض ، بدا سداسي الشكل المعيني ك "ثقب" في مجموعة من 12 ثلاثي المعبد:



في البداية كان يسمى النجمة ذات 20 نقطة. ولكن بعد ذلك ارتبط مع أوصاف في الأدب على متعدد السطوح ، وحدد بأنه RS.

وفي الوقت نفسه ، اكتسبت فكرة إنشاء كائنات من العناصر المعينية شعبية أكثر فأكثر. انضم Michael Longe Higgins ، عالم المحيطات وخبير في تشكيل موجة المحيط ، إلى الهواية الجماعية ، وفي عام 1987 حصل على براءة اختراع لعبة تعتمد على عناصر rhombohedral ، حيث كان من الممكن تجميع "Kepler star" (RS) أو "Kepler ball" (المعيني الثلاثين ):



وعلى الرغم من أنني اكتشفت عن ذلك الآن فقط ، فإن كتل rhombohedral التي اعتبرناها في عام 2009 كخيار لإنشاء "Shipastiks" ، تم إنتاجها فعليًا من قِبل شركة Dextro Mathematical Toys (Rhombo.com) ، والتي عملت في قاعدة Longge-Higgins في San دييغو

مسألة ملء الفراغ بنجاح بأشكال ثلاثية الأبعاد - أو حتى طائرة ذات أشكال ثنائية الأبعاد - معقدة إلى حد ما. من المعروف منذ الستينيات أنه في الحالة العامة ، فإن مشكلة ما إذا كانت مجموعة معينة من النماذج يمكنها ملء الطائرة غير قابلة للحل. (من حيث المبدأ ، يمكن التحقق مما إذا كان يمكن تكوين 1000 من هذه النماذج مع بعضها البعض ، ولكن كلما زادت النماذج التي نراها ، زادت موارد الحوسبة التي يتطلبها ذلك).

ربما افترض أشخاص مثل كيبلر أنه إذا كانت مجموعة من الأشكال يمكن أن تملأ الطائرة ، فيمكن القيام بذلك كنمط متكرر. ومع ذلك ، بعد أن أصبح من الواضح أنه في الحالة العامة لم يتم حل هذه المشكلة ، توصل روجر بنروز في عام 1974 إلى شكلين يمكنهما ملء الطائرة دون تكرار الأنماط. بحلول عام 1976 ، توصل Penrose (و Robert Ammann) إلى نسخة مبسطة من هذه الأشكال:



ونعم ، هذه الأشكال تبدو مثل المعين ، ولكن ليس الذهب. ولكن مع زوايا 36 درجة ، 144 درجة و 72 درجة ، 108 درجة ، لديهم التماثل 5 أضعاف و 10 أضعاف.

لا يمكن لهذه المعين وضع أنماط متكررة. لكن اتضح أنه يمكنهم وضع نمط مبني بطريقة متداخلة بشكل منتظم:



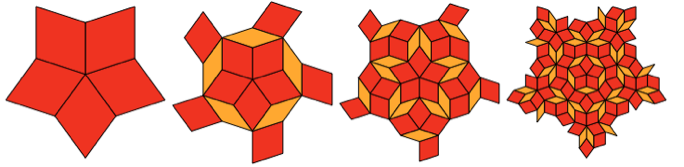
ونعم ، الجزء الأوسط من الخطوة الثالثة يشبه إلى حد بعيد Shipastik بالارض. لكنها لا تتزامن تمامًا مع ذلك ، يكون تنسيق المعين الخارجي مختلفًا قليلاً.

ومع ذلك ، لا يزال هناك اتصال وثيق بينهما. تخيل أننا لن نبدأ من طائرة ، ولكن من نصف مربع ثلاثي الأبعاد ثلاثي الأبعاد ، يتكون من المعين الذهبي:



من الأعلى ، يبدو تمامًا بداية تصميم الفسيفساء Penrose المتداخل. إذا واصلنا هذه العملية ، فسوف نحصل على هذه الفسيفساء:



إذا نظرت إليها "من الجانب" ، يمكنك أن ترى أنها لا تزال نفس المعين الذهبي:



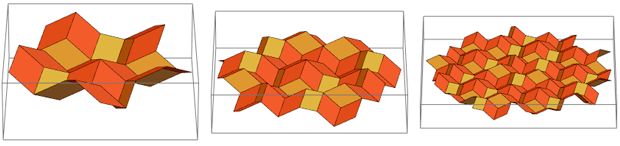
بعد تجميع أربعة من هذه "أسطح Wieringa" ، يمكنك الحصول على RS فقط:



ما هي العلاقة بين هذه الهياكل المدمجة والطريقة الحقيقية لتشكيل البلورات الجسدية؟ ليس واضحا بعد. لكن من المثير للاهتمام أن نرى كيف تظهر تلميحات RS في الطبيعة.

تاريخياً ، بفضل المناقشة حول البلورات البلورية ، بدأ Sandor Kabaei في دراسة RS باستخدام Mathematica ، مما دفع إريك وينشتاين إلى اكتشافها ، مما أدى إلى إدراجها في Mathematica و Wolfram Language ، مما دفعني إلى اختيار واحدة منها لشعارنا. تكريما لهذا ، نطبع الفسيفساء Penrose داخل ورقة Shipastik لدينا:

تسطيح ثورن

انفجرت السفينة Shipastik for Wolfram | Alpha في العالم عام 2009 بعد إصدار Wolfram | Alpha. ولكن لدينا أيضا Shipastik لدينا ل Mathematica ، التي تم تطويرها وتتطور لفترة طويلة. لذلك ، عندما بنينا مقرنا الأوروبي الجديد في عام 2011 ، تنافست شركتا Shipastik على التواجد فيه.

توصل المخرج الفني لدينا منذ فترة طويلة جيريمي ديفيس إلى ما يلي: خذ واحدة من Shipastiks و "جعله مثاليًا" باستخدام "هيكله العظمي" فقط. قرار البدء بـ RS كان قرارًا بسيطًا. ولكن بعد ذلك قمنا بتسويتها ، وهكذا ظهرت النسخة الأولى من الشعار المألوف الآن:

مفاجأة برازيلية

عندما بدأت هذه المقالة ، اعتقدت أن القصة بأكملها ستنتهي هناك. بعد كل شيء ، لقد وصفت بالفعل كيف اخترنا RS لأنفسنا ، وكيف توصل علماء الرياضيات معها. لكن قبل أن أنهيت الكتابة ، قررت: "سأنظر في جميع الرسائل حول Shipastik طوال السنوات ، فقط للتأكد من أنني لم أفتقد أي شيء".

ثم لاحظت رسالة بريد إلكتروني من يونيو 2009 من الفنانة البرازيلية يولاندا كيبريانو. كتبت أنها شاهدت مقالًا عن Wolfram | Alpha في مجلة أخبار برازيلية ، ولفت الانتباه إلى Shipastika ، وقدمت رابطًا لموقعها. لقد مرت أكثر من 9 سنوات منذ ذلك الحين ، لكنني ما زلت أتابع هذا الرابط ، وقد دهشت لرؤية ما يلي:



واصلت قراءة رسالتها: "في البرازيل ، يسمى هذا الكائن Giramundos أو" زهرة Mandakaru "وهو مصنوع من المناديل كزينة فنية."

ماذا؟ في البرازيل ، هناك تقليد مرتبط بشركة Shipastik ، ولم نسمع عنه طوال السنوات الماضية؟ سرعان ما اكتشفت صوره على الشبكة. تم تصنيع جزء صغير من النماذج من الورق ، وكان معظمها مصنوعًا من القماش - ولكن كان هناك الكثير منها:



كتبت إلى صديقي البرازيلي الذي عمل على الإصدارات الأولى من Wolfram | Alpha. أجاب بسرعة: "هذه الأشياء تبدو مألوفة حقًا. لعاري ، لم تكن لدي رغبة كافية لمقارنة اثنين واثنين "، وأرسلت لي صوراً من الكتالوج المحلي للأعمال الفنية والحرفية:



بدأت عملية البحث: ما هي هذه الأشياء ومن أين أتوا؟ قال شخص من شركتنا أن جدته الكبيرة من تشيلي كروشيه مثل هذه الأشياء ، وجعلتها دائمًا ذيلًا. بدأنا في التواصل مع الأشخاص الذين نشروا صورًا لـ "shipastiks الشعبية" على الشبكة. في كثير من الأحيان اتضح أنهم اشتروا نسخهم في المتاجر. ولكن في بعض الأحيان قال الناس أنهم يعرفون كيفية صنعها. وكان لدى الجميع نفس القصة تقريبًا: لقد تعلموا هذا من جداتهم.

من الطرق النموذجية لجمع المسامير الشعبية - على الأقل في عصرنا - قطع 60 ماسة من الورق المقوى. ثم يحتاج الجميع إلى لفهم في القماش ، وخياطة لهم معا:



ولكن بعد ذلك تنشأ مشكلة رياضية على الفور. هل هؤلاء الأشخاص يقومون بتمييز ونحت المعين الذهبي بشكل صحيح بزاوية 63 درجة؟ عادة لا. أنها تجعل المعين مع 60 درجة من أزواج من مثلثات متساوية الأضلاع - وهذا هو الشكل المعيني القياسية المستخدمة في تصنيع لحاف. إذا كيف يحدث الثورنيز؟ حسنًا ، الفرق بين 60 درجة و 63 درجة صغير ، وإذا قمت بخياطة الوجوه معًا ، فستكون هناك مساحة كافية بينهما للمناورة ، لذلك من السهل جدًا إنشاء مجسم متعدد السطوح دون تحقيق زوايا دقيقة تمامًا. (هناك أيضًا شبه - Shipastiks ، والتي ، كما هو الحال في بناء Unkelbach ، بدلاً من الوجوه ، لا توجد معابر رمش ، ولكن "مثلثات خارجية حادة").

تم تعيين المسامير على الإنترنت بشكل مختلف. في معظم الأحيان - Giramundos. غالبًا ما يطلق عليهم Estrelas da Felicidade ("نجوم السعادة"). إن حقيقة ما يطلق عليه أحيانًا "نجوم مورافيا" أمر مثير للارتباك ، ولكن في الواقع ، فإن النجوم المورافيا هي أشكال متعددة السطوح أكثر حدة (غالبًا ما تكون مصنوعة من rhombocubooctahedron) ، والتي اكتسبت مؤخرًا شعبية كمصابيح.

على الرغم من التحقيق المطول ، ما زلت لا أعرف التاريخ الكامل للطفرات الشعبية. إليكم ما اكتشفته.أولاً ، تتركز معظم الطفرات الشائعة اليوم في البرازيل (على الرغم من أن لدينا قصصًا عن ظهورها في أماكن أخرى). ثانياً ، يبدو التقليد قديمًا تمامًا ، فقد ظهر بالتأكيد قبل وقت طويل من القرن العشرين ، وربما قبل عدة قرون. بقدر ما أستطيع أن أقول ، يتم تمريره من الفم إلى الفم ، كما هو الحال عادة مع الفن الشعبي ، ولم أجد أي وثائق تاريخية حقيقية حول هذا الموضوع.

قدمت لي أفضل المعلومات من قبل شخص ما بولا غيرا ، الذي باع المسامير الشعبية في مقهى سياحي تمكنت من إدارته قبل عشر سنوات ، ويقع في مدينة ساو لويس دو بارايتينغ التاريخية. قالت إن الناس من جميع أنحاء البرازيل أتوا إلى المقهى الخاص بهم ، وشاهدوا طفرات شعبية ، وقالوا شيئًا مثل "لم أر مثل هذه الأشياء منذ حوالي 50 عامًا".

علمت باولا نفسها عن المسامير الشعبية (تسميها "نجوم") من امرأة كبيرة السن كانت تعيش في مزرعة عائلية ، والتي كانت تصنعها منذ أن كانت فتاة ، وتعلمت ذلك من والدتها. كانت عمليتها - على ما يبدو عملية نموذجية - تتألف من جمع الورق المقوى في مكان ما (في الأصل كان يشبه صناديق الصناديق) ، وتغطي القطع بقطعة قماش وتضعها معًا للحصول على جسم بحجم 15 سم.

كم عمر شائك الشعبية؟ لا يمكن تقدير ذلك إلا من خلال التقاليد الشفوية. لقد وجدنا العديد من الأشخاص الذين رأوا كيف تم صناعة السفن من قبل أقاربهم المولودين في منطقة 1900. قالت باولا إنها قبل عشر سنوات التقت بامرأة تبلغ من العمر 80 عامًا أخبرتها أنها عندما كانت تربي في مزرعة للبن قبل 200 عام ، كان هناك رف كامل حيث كانت هناك طفرات شعبية صنعتها أربعة أجيال من النساء.

يبدو أن جزءًا من تاريخ shipastik الوطني يدور حول التقاليد المنقولة من الأم إلى الابنة. يقال إن الأمهات غالبا ما يصنعن المسامير كهدايا زفاف لبناتهن. عادةً ما كان يصنع السفن من قصاصات من الملابس وأشياء أخرى تذكّر البنات بطفولتهن - وهو ما يشبه لحاف الترقيع اليوم بالنسبة للأطفال الذين يذهبون إلى الجامعة.

ومع ذلك ، تم اكتشاف تطور آخر بالطفرات الشعبية: في كثير من الأحيان قبل الخياطة على لعبة ، وضعت الأم الأموال التي يمكن أن تستخدمها ابنتها في الحالات الحرجة. وأبقت ابنتها على shipastik جنبا إلى جنب مع لوازم الخياطة لها ، حيث كان زوجها بالكاد وجدته. تم استخدام بعض المسامير كدبابيس وسادة - والتي قد تكون بمثابة عقبة إضافية أمام الأزواج.

ما هي العائلات التي دعمت تقليد صنع المسامير الشعبية؟ منذ حوالي عام 1750 ، كان هناك العديد من مزارع البن والسكر في المناطق الريفية في البرازيل ، بعيدة عن المدن. حتى القرن العشرين تقريبًا ، كان المزارعون يأخذون الفتيات إلى عرائسهم - وغالبًا ما يكونون صغارًا ، وحتى 13 عامًا - من المدن النائية. ربما كانت هذه العرائس - التي تأتي عادة من عائلات جيدة من أصل برتغالي ، مع تعليم جيد نسبيا - تحمل الأشواك الشعبية.

على ما يبدو ، مع مرور الوقت ، امتدت التقاليد إلى الأسر الأسوأ ، وبقيت هناك أساسًا. لكن في مكان ما في منتصف القرن العشرين - ربما عندما بدأت الطرق في الظهور في البلاد ، بدأ التحضر وبدأ الناس في مغادرة المزارع - كاد التقليد أن ينتهي. ومع ذلك ، في المدارس الريفية في جنوب البرازيل في الخمسينيات من القرن الماضي ، تم تعليم الفتيات في فصول فنية لصنع المسامير الشعبية مع فتحة خاصة لاستخدامها كبنوك خنزير.

المسامير الشعبية لها تاريخ مختلف في أجزاء مختلفة من البرازيل. في المناطق الحدودية الجنوبية (بالقرب من الأرجنتين وأوروغواي) هناك تقليد يقول "نجم سانت تم صنع ميغيل (وهي أيضًا سفينة سفينة وطنية) في القرى من قبل المعالجات (أي "الساحرات") اللائي كان يتعين عليهن أثناء تصنيع الألعاب التفكير في صحة المريض.

في أجزاء أخرى من البرازيل ، كانت الألعاب تسمى غالبًا أسماء الزهور والفواكه التي تشبهها قليلاً. في الشمال الشرقي - فلور Mandacarú (باسم الزهور الصبار). في الأراضي الرطبة الاستوائية - Carambola (تكريما لثمار carambola ، التي تسمى أحيانا "النجوم الاستوائية"). في المناطق المشجرة المركزية - Pindaíva (على شرف الفاكهة شائك الحمراء).



ولكن في أكثر الأحيان ، تسمى السفينة الشراكتية الشهيرة Giramundo ، وهي كلمة برتغالية قديمة تعني حرفيًا "عالم يحوم". على ما يبدو ، كانت الألعاب تستخدم كتمائم تجلب الحظ السعيد مع دورانها في مهب الريح. بدأت ذيول تعلق عليها في الآونة الأخيرة ، ولكن ، على ما يبدو ، كان من المعتاد أن نعلقها في المنازل ، وربما في أيام العطلات.

غالبًا ما يكون من غير الواضح أي من التقاليد التي أدت إلى ظهور shipastika كانت أصلية والتي ظهرت مؤخرًا. في موكب عيد الغطاس (الاسم المحلي هو "يوم الملوك الثلاثة") في ساو لويس دو باريتينج ، استخدمت المسامير الشعبية كرمز لنجم بيت لحم - لكن هذا ، على ما يبدو ، ليس تقليدًا قديمًا جدًا ، ومن الواضح أنه لا يظهر أي روابط مع الدين.

وجدنا عدة أمثلة على المسامير الشعبية التي تظهر في المعارض الفنية. قام المهندس المعماري لينا بو باردي بتنظيم إحداها ، التي عقدت في عام 1963 ، ومكرسة للفنون الشعبية في شمال شرق البرازيل. الآخر ، حيث تم عرض أكبر المسامير ثلاثية الأبعاد التي رأيتها ، تم تنظيمها في عام 1997 من قبل المهندس المعماري والمصمم فلاديفيو إمبيريو:



من أين أتت الطفرات الشعبية؟ ما زلت لا أعرف هذا. يمكن أن تظهر في البرازيل ، ويمكن أن تأتي من البرتغال أو جزء آخر من أوروبا. قد تكون حقيقة أنهم استخدموا قطعًا من القماش والخياطة لتصنيعها حججًا لصالح أصلهم الأفريقي أو الأمريكي الأصلي.

قالت إحدى المصنّفات الحديثات اللائي يصنعن صناعة السفن إن جدتها العظيمة - التي صنعت مثل هذه الألعاب ولدت في نهاية القرن التاسع عشر - جاءت من منطقة في إيطاليا تُدعى Romagna (وقالت أخرى إنها تعلمت أن تصنع shipastiks من جدتها التي جاءت من كنديين فرنسيين). أعتقد أنه من الممكن تمامًا أن تكون الطفرات الشعبية شائعة في أوروبا ، ولكنها توفي قبل أجيال عديدة ، ولم ينج هذا التقليد هناك. وعلى الرغم من ظهور الكثير من تعدد السطوح المتعددة الوجوه في اللوحات الأوروبية التي تعود إلى القرون السابقة ، إلا أنني لست على علم بأي من صور شيباستيك بينهم (كما أنني لم أشاهد شيباستيك في الفن الإسلامي).

لكنني متأكد من أن الطفرات الشعبية لها نقطة أصل واحدة. مثل هذا الشيء كان من الصعب اختراعه مرتين.

يجب أن أقول أن هذه ليست مطاردة لي الأولى في مجال الفن. تبين أن البحث عن النمط الأول المضمن ( Sierpinski ) كان أكثر نجاحًا - مما أدى بي في النهاية إلى سرداب الكنيسة الإيطالية ، حيث شاهدت كيف تم اكتشاف هذا النمط تدريجيًا باستخدام مثال من الفسيفساء الحجرية التي يعود تاريخها إلى القرن الثالث عشر.

حتى الآن ، لم يستسلم Shipastik بهذه السهولة - ويعقد الموقف هو حقيقة أنه تم تصنيعه بشكل أساسي من القماش الذي لا يظل جيدًا مثل الحجر.

المسامير تأتي في الحياة

أيا كان أصلها ، تلعب Shipastik دور شعار قوي وجدير. لكن في بعض الأحيان يكون من الممتع إحياء Shipastik - وعلى مر السنين ، قمنا بإنتاج العديد من Shipastiks المخصصة لأسباب مختلفة:



عند استخدام Wolfram | Alpha ، يعرض النظام عادةً Shipastik هندسية. ولكن في بعض الأحيان ، ينشط طلبك - على سبيل المثال ، طلبات π في يوم pi:

blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4

المسامير إلى الأبد

تعدد الوجوه أبدية. يمكن رؤيتها في صورة قبل 500 عام ، والتي تبدو واضحة وحديثة مثل متعدد السطوح على جهاز الكمبيوتر الخاص بي.

قضيت الكثير من وقتي في البحث عن أشياء حوسبية مجردة (على سبيل المثال ، الأوتوماتة الخلوية). لديهم أيضا بعض الخلود. لكن بالنسبة لهم لم أجد أي دليل تاريخي. مثل الكائنات المجردة ، يمكن إنشاؤها في أي وقت. لكن ظهرت اليوم بفضل منصاتنا وأدواتنا المفاهيمية - ولم يرها أحد من قبل.

التاريخ الغني وثبات متعدد الوجوه عمره آلاف السنين. في المظهر ، أنها تشبه الأحجار الكريمة. العثور على متعدد السطوح الصحيح من نوع معين يشبه العثور على جوهرة في عالم هندسي من جميع الأشكال الممكنة.



RS هي واحدة من هذه الأحجار المذهلة ، ودراسة خصائصها ، بدأت أقدر ذلك أكثر. لكنه أيضًا جوهرة لها تاريخ بشري - ومن المثير للاهتمام بشكل كبير أن نرى كيف يمكن لهذا التجريد مثل متعدد السطوح أن يوحد الناس من جميع أنحاء العالم بمثل هذا التاريخ والأهداف المختلفة.

من كان أول من اخترع سداسي الشكل المعيني؟ نحن لا نعرف ، وربما لا نعرف أبدا. ولكن الآن بعد أن حصلنا عليه ، سيبقى معنا إلى الأبد. بلدي متعدد السطوح المفضل.