تقدير الاتجاه المكاني ، أو كيف لا تخافوا من مرشحات ماهوني وماجويك

عن ماذا نتحدث؟

كان ظهور Habre لمشاركة حول مرشح Majwik حدثًا رمزيًا بطريقته الخاصة. على ما يبدو ، فإن الحماس العام للطائرات بدون طيار أحيا الاهتمام بمهمة تقييم اتجاه الجسم عن طريق القياسات بالقصور الذاتي. في الوقت نفسه ، توقفت الطرق التقليدية القائمة على مرشح Kalman عن إرضاء الجمهور - إما بسبب المتطلبات العالية للموارد الحوسبية التي كانت غير مقبولة للطائرات بدون طيار ، أو بسبب الإعدادات المعقدة وغير السهلة.

رافق المنشور تطبيق مضغوط وفعال للغاية للمرشح على C. ومع ذلك ، واستنادا إلى التعليقات ، ظل المعنى المادي لهذه الشفرة ، وكذلك المادة بأكملها ، غامضا بالنسبة لشخص ما. حسنًا ، نحن نعترف بصدق: مرشح Majwik هو الأكثر تعقيدًا في مجموعة المرشحات التي تعتمد بشكل عام على مبادئ بسيطة وأنيقة للغاية. سوف ننظر في هذه المبادئ في منصبي. الرمز لن يكون هنا. إن نشرتي ليست قصة عن تنفيذ محدد لخوارزمية تقدير الاتجاه ، ولكنها دعوة لاختراع الأشكال الخاصة بك حول موضوع معين ، والتي يمكن أن تكون كثيرة.

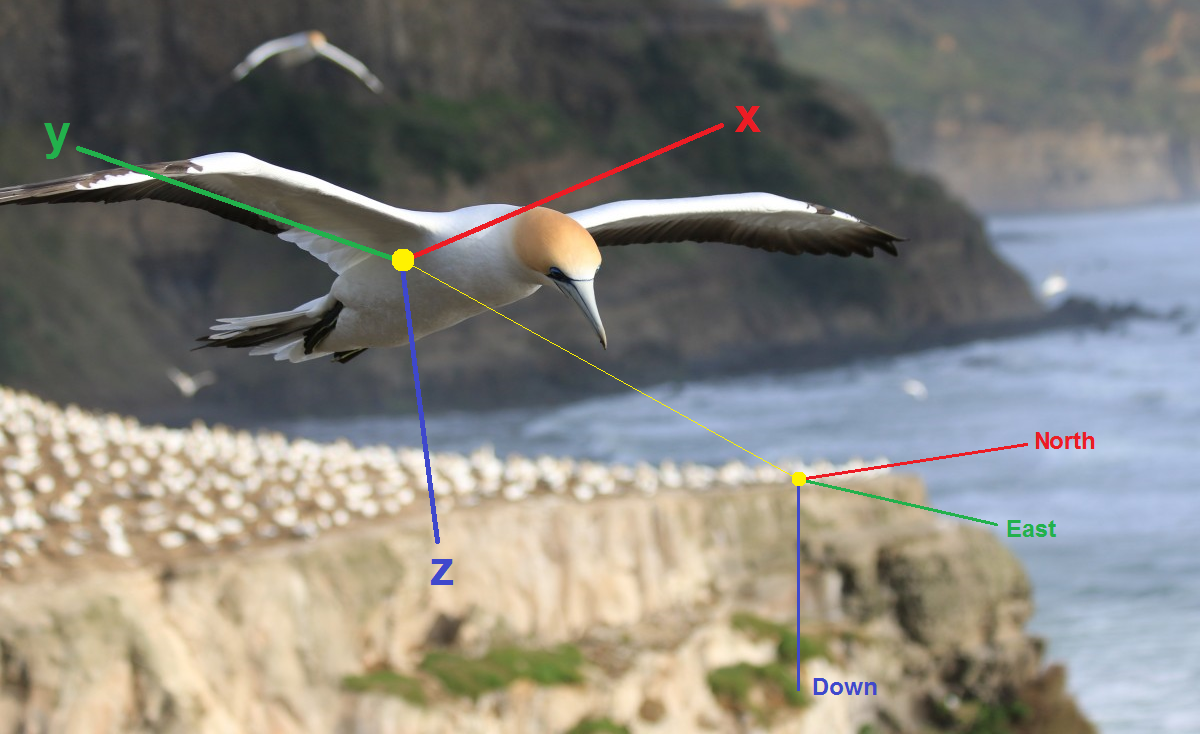
عرض الاتجاه

أذكر الأساسيات. لتقييم اتجاه الجسم في الفضاء ، تحتاج أولاً إلى تحديد بعض المعلمات التي تحدد معًا هذا الاتجاه بشكل فريد ، أي أساسا اتجاه نظام الإحداثيات المرتبط $$$xyz$ النظام الثابت المشروط نسبيًا - على سبيل المثال ، النظام الجغرافي NED (الشمال ، الشرق ، الأسفل). فأنت بحاجة إلى إنشاء معادلات حركية ، على سبيل المثال التعبير عن معدل تغيير هذه المعلمات من خلال السرعة الزاوية من الجيروسكوبات. أخيرًا ، يحتاج المرء إلى إدخال قياسات ناقلات من مقاييس التسارع ومقاييس المغنطيسية وغيرها في الحساب. فيما يلي أكثر الطرق شيوعًا لتمثيل التوجه:

زوايا أويلر - لفة (لفة ، $$$\ phi$ ) ، الملعب (الملعب ، $$$\ theta$ ) ، بالطبع (العنوان ، $$$\ psi$ ) هذه هي المجموعة الأكثر بديهية والأكثر إيجازًا من معلمات الاتجاه: عدد المعلمات يساوي تمامًا عدد درجات الحرية الدورانية. بالنسبة لهذه الزوايا ، يمكننا كتابة المعادلات الحركية لـ Euler . إنهم مغرمون جداً بالميكانيكا النظرية ، لكن في مشكلات الملاحة لا تُستخدم إلا قليلاً. أولاً ، لا تسمح معرفة الزوايا بالتحويل المباشر لمكونات أي متجه من جهاز متصل بنظام إحداثيات جغرافية أو العكس. ثانياً ، عند درجة 90 ± درجة ، تتدهور المعادلات الحركية ، وتصبح الدورة والمقرر إلى أجل غير مسمى.

مصفوفة الدوران - المصفوفة $$$\ mathbf {C}$ 3 × 3 حجم ، والتي تحتاج إلى ضرب أي متجه في نظام الإحداثيات المرتبط للحصول على نفس المتجه في النظام الجغرافي: $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ . المصفوفة دائمًا متعامدة ، أي $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ . المعادلة الحركية لها الشكل $$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ .
هنا $$$\ mathbf {\ Omega}$ - مصفوفة من مكونات السرعة الزاوية تقاس الجيروسكوبات في نظام إحداثيات متصل:

$$

$$\ mathbf {\ Omega} = \ تبدأ {bmatrix} 0 & - \ omega_ {z} & \ omega_ {y} \\ \ omega_ {z} & 0 & - \ \ omega_ {x} \\ - \ omega_ {y } & \ omega_ {x} & 0 \\ \ end {bmatrix}$$

إن مصفوفة الدوران أقل وضوحًا قليلاً من زوايا Euler ، ولكن على عكسها ، فهي تتيح لك تحويل المتجهات مباشرة ولا تفقد المعنى في أي موضع زاوي. من وجهة نظر حسابية ، فإن العيب الرئيسي هو التكرار: من أجل ثلاث درجات من الحرية ، يتم تقديم تسع معلمات دفعة واحدة ، وكلها تحتاج إلى تحديث وفقًا للمعادلة الحركية. يمكن تبسيط المشكلة قليلاً باستخدام التعامد بين المصفوفة.

رباعي الدوران هو علاج جذري ولكنه غير بديهي للغاية ضد التكرار والانحطاط. هذا كائن مكون أربعة. $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ - ليس رقمًا ، وليس متجهًا ، وليس مصفوفة. يمكن رؤية الربع من زاويتين. أولا ، ماذا عن المبلغ الرسمي للعدد $$$q_ {0}$ وناقلات $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ اين $$$\ mathbf {i}، \ mathbf {j}، \ mathbf {k}$ - متجهات محور الوحدة (والتي ، بالطبع ، تبدو سخيفة). ثانياً ، كتعميم للأرقام المعقدة ، حيث نستخدم الآن ليست واحدة ، ولكن ثلاث وحدات وهمية مختلفة $$$\ mathbf {i}، \ mathbf {j}، \ mathbf {k}$ (والذي لا يبدو أقل سخافة). كيف يرتبط رباعي بدوره؟ من خلال نظرية أويلر: يمكن دائمًا نقل الجسم من اتجاه معين إلى آخر مع دوران محدود بزاوية $$$\ alpha$ حول بعض المحور مع ناقل دليل $$$\ mathbf {u}$ . يمكن دمج هذه الزاوية والمحور في رباعي: $$$\ mathbf {q} = \ mathrm {cos} (\ alpha / 2) + \ mathbf {u} \ mathrm {sin} (\ alpha / 2)$ . مثل المصفوفة ، يمكن استخدام رباعي لتحويل مباشرة أي ناقل من نظام إحداثي إلى آخر: $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {- 1}$ . كما ترون ، فإن التمثيل الرباعي للاتجاه يعاني أيضًا من التكرار ، ولكنه أقل بكثير من المصفوفة: المعلمة الإضافية واحدة فقط. كان الاستعراض الشامل ل quaternions بالفعل على حبري . تحدثوا عن الهندسة والرسومات ثلاثية الأبعاد. نحن مهتمون أيضًا بالحركية ، حيث يجب أن يكون معدل التغير في الربع مرتبطًا بالسرعة الزاوية المقاسة. المعادلة الحركية المقابلة لها الشكل $$$\ dot {\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ اين المتجه $$$\ mathbf {\ omega}$ يعتبر أيضا رباعي مع جزء العددية صفر.

تصفية مخططات

تتمثل الطريقة الأكثر سذاجة في حساب الاتجاه في تسليح معادلة حركية وتحديثها وفقًا لأي مجموعة من المعلمات التي نحبها. على سبيل المثال ، إذا اخترنا مصفوفة دوران ، فيمكننا كتابة دورة بها شيء بروح C += * Omega * dt . النتيجة سوف يخيب. تتميز الجيروسكوب ، وخاصةً ممس ، بإزاحة صفرية كبيرة وغير مستقرة - ونتيجة لذلك ، حتى في حالة الراحة الكاملة ، سيكون للاتجاه المحسوب خطأ غير محدود في التراكم (الانجراف). جميع الحيل التي اخترعها ماهوني وماجويك والعديد من الحيل الأخرى ، باستثناءي ، كانت تهدف إلى تعويض هذا الانجراف عن طريق إشراك القياسات من مقاييس التسارع ومقاييس المغنطيسات وأجهزة استقبال الشبكات العالمية لسواتل الملاحة وتأخرها ، إلخ. وهكذا ولدت مجموعة كاملة من مرشحات التوجيه ، بناءً على مبدأ أساسي بسيط.

المبدأ الأساسي. للتعويض عن انجراف الاتجاه ، من الضروري إضافة السرعة الزاويّة المقاسة بواسطة الجيروسكوبات إلى سرعة زاويّة تحكم إضافية مبنية على أساس قياسات المتجهات لأجهزة الاستشعار الأخرى. يجب أن يسعى متجه السرعة الزاوية للتحكم إلى الجمع بين اتجاهات المتجهات المقاسة واتجاهاتها الحقيقية المعروفة.

يتم اتباع نهج مختلف تمامًا هنا عن بناء مصطلح تصحيح مرشح Kalman. الفرق الرئيسي هو أن السرعة الزاوية للتحكم ليست مصطلحًا ، ولكن عاملًا للقيمة المقدرة (المصفوفة أو الربع). مزايا هامة تتبع من هذا:

• يمكن بناء مرشح تقييم للاتجاه نفسه ، وليس للانحرافات الصغيرة للاتجاه عن تلك التي توفرها الجيروسكوبات. علاوة على ذلك ، ستلبي القيم المقدرة تلقائيًا جميع المتطلبات التي تفرضها المهمة: المصفوفة ستكون متعامدة ، وتم تطبيع الربع.
• المعنى المادي للسرعة الزاوية للتحكم أكثر وضوحًا من مصطلح التصحيح في مرشح Kalman. تتم جميع عمليات التلاعب مع المتجهات والمصفوفات في الفضاء المادي ثلاثي الأبعاد العادي ، وليس في مساحة دولة متعددة الأبعاد مجردة. يعمل ذلك على تبسيط عملية تصفية المرشح وتعديله بشكل كبير ، وكميزة إضافية يتيح لك التخلص من المصفوفات ذات البعد الكبير ومكتبات المصفوفات الثقيلة.

الآن دعونا نرى كيف يتم تطبيق هذه الفكرة في خيارات مرشح معين.

مرشح ماهوني. كُتبت جميع الرياضيات الغاضبة لمقال ماهوني الأصلي لتبرير المعادلات البسيطة (32). نعيد كتابتها في تدويننا. إذا تجاهلنا تقدير التشريد الصفري للجيروسكوبات ، فستبقى معادلتان أساسيتان - المعادلة الحركية لمصفوفة الدوران نفسها (مع السرعة الزاوية للتحكم في شكل مصفوفة $$$\ mathbf {\ Omega} '$ ) وقانون تشكيل هذه السرعة جدا في شكل ناقل $$$\ mathbf {\ omega} '$ . للبساطة ، نفترض أنه لا توجد تسارع أو التقاطات المغناطيسية ، وبفضل هذا ، تتوفر قياسات تسارع السقوط الحر لنا. $$$- \ hat {\ mathbf {g}} _ {xyz}$ من التسارع والحقل المغناطيسي للأرض $$$\ hat {\ mathbf {m}} _ {xyz}$ من المغنطيسية. يتم قياس كلا المتجهين بواسطة أجهزة استشعار في نظام إحداثيات متصل ، وفي النظام الجغرافي يعرف موقعهما: $$$- \ mathbf {g} _ {NED}$ لافتا $$$\ mathbf {m} _ {NED}$ - إلى الشمال المغناطيسي. عندئذٍ ستبدو معادلات مرشح Mahoney كما يلي:

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} (\ mathbf {\ Omega} + \ mathbf {\ Omega} ') \\ \ mathbf {\ omega'} = k_ {g} \ hat {\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

دعونا ننظر بعناية في المعادلة الثانية. المصطلح الأول على الجانب الأيمن هو منتج متجه. العامل الأول فيه هو تسارع الجاذبية المقاس ، والثاني صحيح. نظرًا لأن العوامل يجب أن تكون في نظام إحداثي واحد ، يتم تحويل العامل الثاني إلى نظام متصل عن طريق ضرب ب $$$\ mathbf {C} ^ {T}$ . السرعة الزاوية ، التي يتم بناؤها كمنتج متجه ، تكون عموديًا على مستوى متجهات العوامل. يسمح لك بتدوير الموضع المقدر لنظام الإحداثيات المرتبط حتى يتزامن متجه العامل في الاتجاه - ثم تتم إعادة تعيين المنتج الموجه إلى الصفر ويتوقف الدوران. معامل $$$k_ {g}$ يحدد صلابة مثل هذه الملاحظات. المصطلح الثاني يؤدي عملية مماثلة مع ناقل مغناطيسي. في الواقع ، يجسد مرشح Mahoney الأطروحة المعروفة: معرفة اثنين من ناقلات غير اللامركزية في نظامين إحداثيات مختلفة تتيح لك لاستعادة التوجه المتبادل لهذه النظم بشكل فريد. إذا كان هناك أكثر من متجهين ، فسيوفر ذلك تكرارًا مفيدًا للقياس. إذا كان هناك متجه واحد فقط ، فلا يمكن تحديد درجة تناوب واحدة من الحرية (الحركة حول هذا المتجه). على سبيل المثال ، إذا تم إعطاء متجه فقط $$$- \ mathbf {g}$ ، ثم يمكنك ضبط الانجراف للفة والملعب ، ولكن ليس بالطبع.

بالطبع ، لا يتعين على مرشح Mahoney استخدام مصفوفة الدوران. هناك أيضًا متغيرات رباعية غير قانونية.

منصة الدوران الافتراضية. في مرشح Mahoney ، قمنا بتطبيق السرعة الزاوية للتحكم $$$\ mathbf {\ omega '}$ لنظام الإحداثيات المرتبط. ولكن يمكنك تطبيقه على الموقع المقدر لنظام الإحداثيات الجغرافية. المعادلة الحركية تأخذ الشكل

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega} - \ mathbf {\ Omega} '\ mathbf {C}$$

اتضح أن هذا النهج يمهد الطريق لتشبيه جسدي مثمر للغاية. يكفي أن نتذكر ما بدأت به تقنية الجيروسكوب - أنظمة الملاحة الرأسية والقصور الذاتي القائمة على منصة مستقرة الدوران في انحراف.


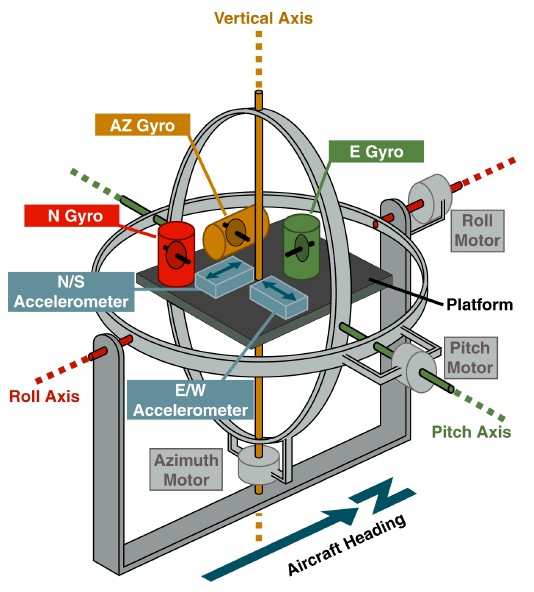www.theairlinepilots.com

الهدف من المنصة كان هناك تجسيد لنظام الإحداثيات الجغرافية. تم قياس اتجاه الموجة الحاملة بالنسبة لهذه المنصة بواسطة مجسات زاوية على إطارات التعليق. إذا كانت الجيروسكوبات قد انجرفت ، فقد انجرفت المنصة أيضًا بعدها ، وتراكمت الأخطاء في قراءات أجهزة استشعار الزاوية. للتخلص من هذه الأخطاء ، تم تقديم التعليقات من مقاييس التسارع المثبتة على المنصة. على سبيل المثال ، انحراف المنصة عن الأفق المحيط بالمحور الشمالي كان ينظر إليه بواسطة مقياس التسارع للمحور الشرقي. سمحت هذه الإشارة ضبط السرعة الزاوية للتحكم $$$\ mathbf {\ omega '}$ إعادة النظام الأساسي إلى الأفق.

يمكننا استخدام نفس المفاهيم البصرية في مهمتنا. يجب عندئذٍ قراءة المعادلة الحركية الموصوفة على النحو التالي: معدل التغير في الاتجاه هو الفرق بين حركات دوران اثنين - الحركة المطلقة للناقل (الفصل الأول) والحركة المطلقة للمنصة الدورانية الافتراضية (المصطلح الثاني). يمكن تمديد التشبيه إلى قانون تشكيل السرعة الزاوية المسيطرة. المتجهات $$$- \ hat {\ mathbf {g}} _ {NED} = - \ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ أنه يمثل شهادة التسارع ، من المفترض أن يقف على منصة الدوران. ثم ، لأسباب مادية ، يمكنك كتابة:

$$

$$\ omega '_ {N} = - gk_ {g} \ hat {g} _ {E}، \؛ \ omega '_ {E} = gk_ {g} \ hat {g} _ {N}$$

قد يكون من الممكن الوصول إلى نفس النتيجة تمامًا بطريقة رسمية ، عن طريق إجراء الضرب المتجهي بروح مرشح Mahoney ، ولكن ليس الآن في نظام متصل ، ولكن في نظام إحداثيات جغرافية. هل هو ضروري فقط؟

يظهر التلميح الأول للتشابه المفيد بين المنصة ونظام الملاحة بالقصور الذاتي ، على ما يبدو ، في براءة اختراع بوينغ القديمة . ثم تم تطوير هذه الفكرة بفعالية بواسطة Salychev ، ومؤخراً - من جانبي أيضًا . المزايا الواضحة لهذا النهج:

• يمكن تشكيل السرعة الزاوية للتحكم على أساس مبادئ فيزيائية مفهومة.
• بطبيعة الحال ، يتم فصل القنوات الأفقية والاتجاهية ، والتي تختلف اختلافًا كبيرًا في خصائصها وأساليب التصحيح. في مرشح Mahoney أنها مختلطة.
• من الملائم التعويض عن تأثير التسارع بسبب استخدام بيانات GNSS ، والتي يتم إصدارها بدقة في المحاور الجغرافية وليس ذات الصلة.
• من السهل تعميم الخوارزمية على حالة الملاحة بالقصور الذاتي عالية الدقة ، حيث من الضروري مراعاة شكل الأرض وتناوبها. كيفية القيام بذلك في مخطط ماهوني ، لا أستطيع أن أتخيل.

مرشح ماجويك. اختار مجويك الطريق الصعب . إذا كان ماهوني ، على ما يبدو ، قد توصل إلى قراره بشكل حدسي ، ثم برر ذلك رياضياً ، فقد أثبت مجويك من البداية أنه شخص شكلي. تعهد بحل مشكلة التحسين. انه سبب ذلك. ضبط اتجاه رباعي الدوران. في الحالة المثالية ، الاتجاه المحسوب لبعض المتجهات المقاسة (دعنا نحصل على هذا $$$- \ mathbf {g}$ ) يتزامن مع الحقيقي. ثم سوف يكون $$${\ mathbf {q}} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ . في الواقع ، لا يمكن تحقيق ذلك دائمًا (خاصة إذا كان هناك أكثر من متجهين) ، ولكن يمكنك محاولة تقليل الانحراف $$$\ mathbf {F} = {\ mathbf {q} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q}} - \ hat {\ mathbf {g}} _ {xyz}$ من المساواة بالضبط. للقيام بذلك ، نقدم معيار التقليل

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

يتطلب الحد الأدنى نزولًا متدرجًا - يتحرك في خطوات صغيرة في الاتجاه المعاكس للتدرج $$$\ nabla E$ ، أي عكس أسرع زيادة في الوظيفة $$$E$ . بالمناسبة ، يرتكب مجويك خطأ: فهو لا يعرض في جميع أعماله $$$E$ ويكتب بإصرار $$$\ nabla \ mathbf {F}$ بدلا من $$$\ nabla E$ ، على الرغم من أنه يحسب فعلا بالضبط $$$\ nabla E$ .

نتيجة لذلك ، يؤدي نزول التدرج إلى الحالة التالية: للتعويض عن اتجاه الاتجاه ، يجب إضافة مصطلح سلبي جديد يتناسب مع المعادلة الحركية من المعادلة الحركية $$$\ nabla E$ :

$$

$$\ dot {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega} - \ beta \ frac {\ nabla E} {| \ nabla E |}$$

هنا يغادر Majwik قليلاً من "مبدأنا الأساسي": فهو لا يضيف مصطلح التصحيح إلى السرعة الزاوية ، ولكن إلى معدل التغير في الربع ، وهذا ليس هو بالضبط نفس الشيء. نتيجة لذلك ، قد يتبين أن الربع المحدّث لم يعد منفردًا ، وبالتالي فقد القدرة على تمثيل الاتجاه. لذلك ، بالنسبة لعامل التصفية Majwik ، يعد التطبيع الاصطناعي للرباعي عملية حيوية ، في حين أنه بالنسبة للمرشحات الأخرى يكون مرغوبًا ، وليس اختياريًا.

تأثير التسارع

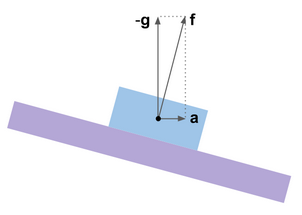
حتى الآن ، تم افتراض أنه لا توجد تسارع حقيقي ومقاييس التسارع تقيس تسارع الجاذبية فقط $$$- \ mathbf {g}$ . جعل ذلك من الممكن الحصول على معيار رأسي ، وبمساعدته ، التعويض عن الانجراف للفة والملعب. ومع ذلك ، في الحالة العامة ، فإن مقاييس التسارع ، بصرف النظر عن مبدأ التشغيل الخاص بها ، تقيس التسارع الظاهر - الفرق المتجه في التسارع الحقيقي والتسارع الجاذبي $$$\ mathbf {f} = \ mathbf {a} - \ mathbf {g}$ . لا يتزامن اتجاه التسارع الظاهر مع العمودي ، وتظهر الأخطاء الناتجة عن التسارع في تقديرات لفة ونبرة.

هذا سهل التوضيح باستخدام تشبيه منصة الدوران الافتراضية. تم تصميم نظام التصحيح الخاص بها بحيث تتوقف المنصة في هذا الموضع الزاوي حيث يتم إعادة تعيين إشارات مقاييس التسارع ، المفترض أن تكون مثبتة عليه ، إلى الصفر ، أي عندما ناقلات قياسها $$$\ mathbf {f}$ يصبح عموديًا على محاور حساسية مقاييس التسارع. إذا لم يكن هناك تسارع ، فإن هذا الموقف يتزامن مع الأفق. عند حدوث تسارع أفقي ، يتم تحويل منصة الدوران. يمكننا أن نقول أن منصة الجيروسكوب تشبه البندول المرتجع بشدة أو الخط السميك.



في التعليقات على المنشور حول مرشح Majwik ، سارع سؤال حول ما إذا كان من الممكن أن نأمل أن يكون هذا المرشح أقل عرضة للتسارع من ، على سبيل المثال ، مرشح Mahoney. للأسف ، جميع المرشحات الموصوفة هنا تستغل نفس المبادئ المادية وبالتالي تعاني من نفس المشاكل. من المستحيل خداع الفيزياء بالرياضيات. ثم ماذا تفعل؟

تم ابتكار الطريقة الأبسط والأصعب مرة أخرى في منتصف القرن الماضي من أجل الدوران العمودية للطيران: لتقليل أو عدم الصفر تمامًا للسرعة الزاوية للتحكم في وجود تسارع أو السرعة الزاوية للدورة (مما يشير إلى الدخول في منعطف). يمكن تطبيق نفس الطريقة على أنظمة النظام الأساسي الحالية. في هذه الحالة ، يجب الحكم على التسارع حسب القيم $$$\ hat {f} _ {N} ، \ hat {f} _ {E}$ لكن لا $$$\ hat {f} _ {x} ، \ hat {f} _ {y}$ والتي بدورها هي صفر. لكن في الحجم $$$\ hat {\ mathbf {f}} _ {NED}$ ليس من الممكن دائمًا التمييز بين التسارع الحقيقي وتوقعات تسارع الجاذبية ، والذي يرجع إلى ميل منصة الدوران ، والتي يجب القضاء عليها. لذلك ، لا تعمل الطريقة بشكل موثوق - لكنها لا تتطلب أي أجهزة استشعار إضافية.

تعتمد الطريقة الأكثر دقة على استخدام قياسات السرعة الخارجية من مستقبل GNSS. إذا كانت السرعة معروفة $$$\ mathbf {v}$ ، ثم يمكن تمييزه عدديًا والحصول على تسارع حقيقي $$$\ dot {\ mathbf {v}}$ . ثم الفرق $$$\ hat {\ mathbf {f}} _ {NED} - \ dot {\ mathbf {v}}$ سوف تكون متساوية تماما $$$- \ hat {\ mathbf {g}} _ {NED}$ بغض النظر عن حركة وسائل الإعلام. يمكن استخدامه كمعيار للرأسي. على سبيل المثال ، يمكنك تحديد السرعة الزاوية للتحكم في منصة الدوران في النموذج

$$

$$\ omega '_ {N} = gk_ {g} (\ hat {f} _ {E} - \ dot {v} _ {E})، \؛ \ omega '_ {E} = - gk_ {g} (\ hat {f} _ {N} - \ dot {v} _ {N})$$

الاستشعار صفر إزاحة

ميزة محزنة من الجيروسكوبات ومقاييس التسارع من فئة المستهلك هي عدم الاستقرار الكبير في التخالفات الصفرية في الوقت ودرجة الحرارة. للتخلص منها ، لا يكفي مجرد معايرة المصنع أو المختبر - تحتاج إلى إعادة التقييم أثناء التشغيل.

الجيروسكوبات. سنتعامل مع صفر إزاحة الجيروسكوبات $$$\ delta {\ mathbf {\ omega}}$ . يتحرك الموضع المقدر لنظام الإحداثيات المرتبط بعيدًا عن موضعه الحقيقي بسرعة زاوي يحددها عاملان متعارضان - التشريد الصفري للجيروسكوبات والتحكم في السرعة الزاوية: $$$\ delta {\ mathbf {\ omega}} - \ mathbf {\ omega '}$ . إذا تمكن نظام التصحيح (على سبيل المثال ، في عامل تصفية Mahoney) من إيقاف الخروج ، فسيكون في الحالة المستقرة $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega '}$ . وبعبارة أخرى ، في السيطرة على السرعة الزاوية $$$\ mathbf {\ omega '}$ معلومات حول اضطراب صالح غير معروف $$$\ delta {\ mathbf {\ omega}}$ . لذلك ، يمكن تطبيق التقدير التعويضي : لا نعرف حجم الاضطراب بشكل مباشر ، ومع ذلك ، فإننا نعرف الإجراء التصحيحي اللازم لموازنته. هذا هو الأساس لتقدير التشريد صفر من الجيروسكوبات. على سبيل المثال ، في ماهوني ، يتم تحديث النتيجة وفقًا للقانون

$$

$$\ dot {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega '}$$

ومع ذلك ، فإن النتيجة غريبة: تصل التقديرات إلى 0.04 rad / s. لا يحدث عدم استقرار هذه الإزاحة الصفرية حتى في معظم الجيروسكوبات السيئة. أظن أن المشكلة تكمن في أن Mahoney لا يستخدم GNSS أو أجهزة استشعار خارجية أخرى - ويتأثر تمامًا بتأثير التسارع. فقط على المحور العمودي ، حيث لا يضر التسارع ، يبدو التقدير أكثر أو أقل قوة:


ماهوني وآخرون ، 2008

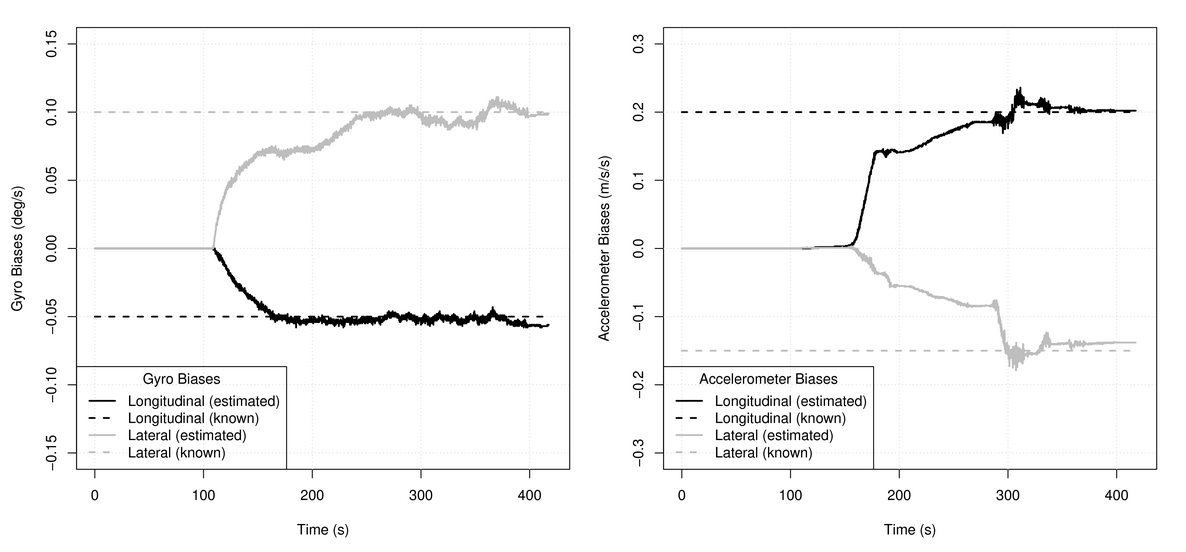
التسارع معدل صفر تسارع الأوفست $$$\ delta {\ mathbf {f}}$ أصعب بكثير. يجب استخراج المعلومات المتعلقة بهم من نفس السرعة الزاوية للتحكم $$$\ mathbf {\ omega '}$ . ومع ذلك ، في الحركة المستقيمة ، لا يمكن تمييز تأثير الإزاحة الصفرية لمقاييس التسارع من ميل الناقل أو انحراف تركيب كتلة المستشعر عليها. لا إضافات ل $$$\ mathbf {\ omega '}$ التسارع لا تخلق. لا تظهر المادة المضافة إلا عند منعطف ، مما يسمح لنا بالفصل وتقييم أخطاء الجيروسكوبات ومقاييس التسارع بشكل مستقل. مثال على كيفية القيام بذلك في مقالتي . إليكم الصور من هناك:

بدلاً من الاستنتاج: ماذا عن مرشح كالمان؟

ليس لدي أدنى شك في أن المرشحات الموضحة هنا ستكون دائمًا ميزة على مرشح Kalman التقليدي من حيث السرعة ، وضغط الشفرة وسهولة الإعداد - لهذا تم إنشاؤها. أما بالنسبة لدقة التقييم ، فكل شيء هنا غير واضح. لقد قابلت مرشحات Kalman المصممة دون نجاح ، والتي كانت بدقة أقل بشكل ملحوظ من المرشح ذي منصة الدوران الافتراضية. أثبت مجويك أيضًا فوائد مرشحه بالنسبة لبعض تقديرات كالمان. ومع ذلك ، بالنسبة لمهمة تقدير الاتجاه نفسها ، يمكنك إنشاء ما لا يقل عن اثنتي عشرة دائرة تصفية Kalman مختلفة ، وسيكون لكل منها إعدادات لا حصر لها. ليس لدي أي سبب للاعتقاد بأن مرشح Mahoney أو Majwik سيكون أكثر دقة من أفضل مرشح Kalman ممكن . وبطبيعة الحال ، سيكون لنهج كالمان دائمًا ميزة العالمية: فهو لا يفرض أي قيود صارمة على الخصائص الديناميكية المحددة للنظام المقيَّم.