هوفمان ضغط البيانات

الدخول

في هذه المقالة سأتحدث عن خوارزمية هوفمان المعروفة ، وكذلك تطبيقها في ضغط البيانات.

نتيجة لذلك ، سنكتب أرشيفي بسيط. كان هناك بالفعل مقال حول هذا الموضوع عن حبري ، لكن دون تطبيق عملي. إن المادة النظرية للوظيفة الحالية مأخوذة من دروس علوم الكمبيوتر بالمدرسة وكتاب روبرت لافور "هياكل البيانات والخوارزميات في جافا". لذلك ، كل شيء تحت الخفض!

القليل من التفكير

في ملف نص عادي ، يتم ترميز حرف واحد بثمانية بتات (ترميز ASCII) أو 16 (ترميز Unicode). كذلك سننظر في ترميز ASCII. على سبيل المثال ، خذ السطر s1 = "SUSIE تقول إنه أمر سهل \ n". في المجموع ، هناك 22 حرفًا في السطر ، بالطبع ، بما في ذلك المسافات وحرف السطر الجديد - '\ n'. سيزن الملف الذي يحتوي على هذا الخط 22 * ​​8 = 176 بت. السؤال الذي يطرح نفسه على الفور: هل من المنطقي استخدام كل 8 بت لتشفير حرف واحد؟ نحن لا نستخدم جميع أحرف ASCII. حتى لو تم استخدامها ، فسيكون من المنطقي بالنسبة للحرف الأكثر تكرارا - S - إعطاء أقصر رمز ممكن ، ولأحرف الحرف - T (أو U ، أو \ \ ') - لإعطاء رمز أكثر أصالة. هذه هي خوارزمية هوفمان: تحتاج إلى العثور على أفضل خيار ترميز ، حيث سيكون الملف أقل وزنًا. من الطبيعي تمامًا أن تختلف أطوال الشفرات لأحرف مختلفة - وهذا هو أساس الخوارزمية.

الترميز

لماذا لا تمنح الحرف "S" رمزًا ، على سبيل المثال ، طوله 1 بت: 0 أو 1. فليكن 1. ثم سنمنح ثاني أكثر الأحرف التي تمت مواجهتها - "(فضاء) - 0. تخيل أنك بدأت في فك تشفير رسالتك - السلسلة المشفرة s1 - وترى أن الكود يبدأ بـ 1. فما العمل: هل هو حرف S ، أم هو شخصية أخرى ، على سبيل المثال A؟ لذلك ، تنشأ قاعدة مهمة:

لا ينبغي أن يكون رمز البادئة من آخر

هذه القاعدة هي المفتاح في الخوارزمية. لذلك ، يبدأ إنشاء الشفرة بجدول التردد ، الذي يشير إلى التردد (عدد مرات الحدوث) لكل حرف:

يجب تشفير الأحرف التي تحتوي على أكبر عدد من الأحداث مع أصغر عدد ممكن من وحدات البت. سأقدم مثالًا على أحد جداول التعليمات البرمجية الممكنة:

وبالتالي ، ستبدو الرسالة المشفرة كما يلي:

10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110 

فصلت رمز كل حرف بمسافة. هذا لن يحدث بالفعل في ملف مضغوط!
السؤال الذي يطرح نفسه: كيف أتت هذه الملحمة برمز ؟ كيف تنشئ جدول أكواد؟ هذا سوف يناقش أدناه.

بناء شجرة هوفمان

هنا أشجار البحث الثنائية تأتي لإنقاذ. لا تقلق ، فهناك طرق البحث والإدخال والحذف غير مطلوبة. هنا هو هيكل شجرة في جافا:

 public class Node { private int frequence; private char letter; private Node leftChild; private Node rightChild; ... } 

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } ... } 

هذا ليس رمزًا كاملاً ، والكود الكامل سيكون أدناه.

هنا خوارزمية بناء الشجرة نفسها:

1. إنشاء كائن عقدة لكل حرف من الرسالة (السطر s1). في حالتنا ، سيكون هناك 9 عقد (كائنات عقدة). تتكون كل عقدة من حقلين للبيانات: الرمز والتردد
2. إنشاء كائن شجرة (BinaryTree) لكل من عقده العقد. تصبح العقدة جذر الشجرة.
3. الصق هذه الأشجار في قائمة الانتظار ذات الأولوية. كلما كان التردد أقل ، كلما زادت الأولوية. وبالتالي ، عند الاستخراج ، يتم تحديد dervo دائمًا بأقل تردد.

بعد ذلك ، عليك القيام بما يلي دوريًا:

1. استخرج شجرتين من قائمة انتظار الأولوية واجعلهما من نسل العقدة الجديدة (العقدة التي تم إنشاؤها حديثًا بدون خطاب). تردد العقدة الجديدة يساوي مجموع ترددات شجرتين متحدرين.
2. لهذه العقدة ، قم بإنشاء شجرة ذات جذر في هذه العقدة. الصق هذه الشجرة مرة أخرى في قائمة انتظار الأولوية. (نظرًا لأن الشجرة لها تردد جديد ، فمن المرجح أن تصل إلى مكان جديد في قائمة الانتظار)
3. تابع الخطوتين 1 و 2 حتى تبقى شجرة واحدة فقط في قائمة الانتظار - شجرة هوفمان

النظر في هذه الخوارزمية على الخط s1:



هنا ، يشير الرمز "lf" (linefeed) إلى الانتقال إلى سطر جديد ، "sp" (مسافة) هي مسافة.

ما التالي؟

لقد حصلنا على شجرة هوفمان. حسنا حسنا. وماذا تفعل به؟ لن يأخذوها مجانًا ، وبعد ذلك ، يتعين عليك تتبع جميع المسارات الممكنة من الجذر إلى أوراق الشجرة. دعنا نوافق على تعيين الحافة 0 إذا كانت تؤدي إلى السليل الأيسر و 1 إذا إلى الحافة اليمنى. بالمعنى الدقيق للكلمة ، في هذه الرموز ، رمز الرمز هو المسار من جذر الشجرة إلى الورقة التي تحتوي على هذا الرمز نفسه.



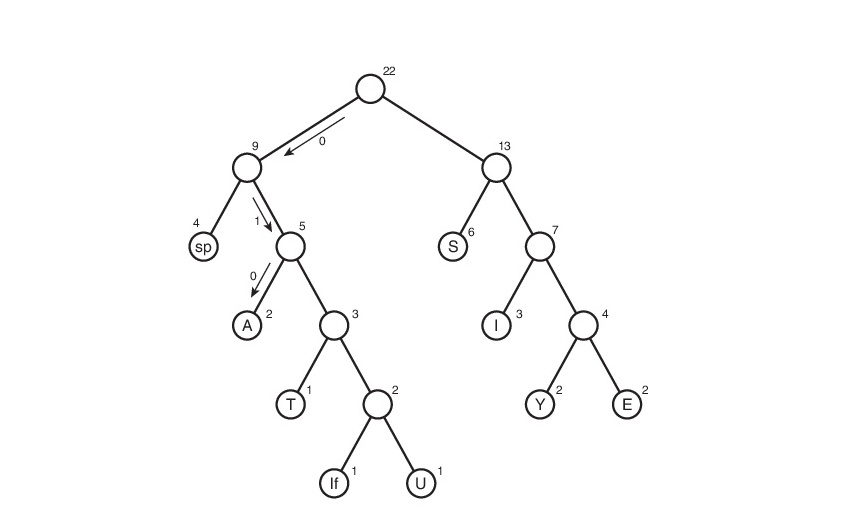
وبالتالي ، تحول جدول الرموز. لاحظ أنه إذا أخذنا في الاعتبار هذا الجدول ، يمكننا أن نستنتج حول "وزن" كل حرف - هذا هو طول الكود الخاص به. ثم يزن الملف المضغوط: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 بت. في البداية ، كان وزنه 176 بت. لذلك ، قمنا بتخفيضه بقدر 176/65 = 2.7 مرة! ولكن هذا هو اليوتوبيا. من غير المرجح الحصول على مثل هذا المعامل. لماذا؟ وسيتم مناقشة هذا في وقت لاحق قليلا.

فك التشفير

حسنًا ، ربما يكون أبسط شيء هو فك التشفير. أعتقد أن الكثير منكم خمن أنه من المستحيل إنشاء ملف مضغوط ببساطة دون أي إشارة إلى كيفية تشفيره - لن نتمكن من فك تشفيره! نعم ، كان من الصعب علي أن أدرك ذلك ، لكن كان عليّ إنشاء ملف نصي table.txt مع جدول ضغط:

 01110 00 A010 E1111 I110 S10 T0110 U01111 Y1110 

سجل الجدول في شكل "حرف" "رمز الحرف". لماذا 01110 بدون شخصية؟ في الواقع ، يكون ذلك برمز ، فقط أدوات java التي استخدمها عند الإخراج إلى ملف ، يتم تحويل حرف السطر الجديد - '\ n' - إلى سطر جديد (بغض النظر عن مدى غباءه). لذلك ، السطر الفارغ أعلاه هو رمز الكود 01110. بالنسبة للرمز 00 ، فإن الحرف هو مسافة في بداية السطر. يجب أن أقول على الفور أن طريقة تخزين هذا الجدول لدينا قد تدعي أنها غير عقلانية. لكنها بسيطة لفهم وتنفيذ. يسرني أن أسمع توصياتكم في التعليقات المتعلقة بالتحسين.

من السهل جدًا فك شفرة هذا الجدول. تذكر القاعدة التي كنا نسترشد بها عند إنشاء الترميز:

يجب أن لا يوجد كود بادئة أخرى

هذا هو المكان الذي تلعب فيه دور تسهيل. لقد قرأنا شيئًا فشيئًا بشكل متتابع ، وبمجرد أن تتطابق السلسلة المستلمة d ، التي تتكون من وحدات بت للقراءة ، مع الترميز المطابق لحرف الحرف ، نعرف على الفور أن حرف الحرف كان مشفرًا (وفقط!). بعد ذلك ، نكتب حرفًا في سطر فك التشفير (السطر الذي يحتوي على الرسالة التي تم فك شفرتها) ، ونصف السطر d ، ثم نقرأ الملف المشفر.

التنفيذ

حان الوقت لإذلال الكود الخاص بي عن طريق كتابة أرشيف. دعنا نسميها ضاغط.

لنبدأ من البداية. أولاً ، نكتب فئة العقدة:

 public class Node { private int frequence;// private char letter;// private Node leftChild;//  private Node rightChild;//  public Node(char letter, int frequence) { //,  this.letter = letter; this.frequence = frequence; } public Node() {}//    (.       ) public void addChild(Node newNode) {//  if (leftChild == null)//  =>  =>    leftChild = newNode; else { if (leftChild.getFrequence() <= newNode.getFrequence()) // ,   rightChild = newNode;// ,     else { rightChild = leftChild; leftChild = newNode; } } frequence += newNode.getFrequence();//  } public Node getLeftChild() { return leftChild; } public Node getRightChild() { return rightChild; } public int getFrequence() { return frequence; } public char getLetter() { return letter; } public boolean isLeaf() {//   return leftChild == null && rightChild == null; } } 

الآن الشجرة:

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } public int getFrequence() { return root.getFrequence(); } public Node getRoot() { return root; } } 

قائمة انتظار الأولوية:

 import java.util.ArrayList;//-,      class PriorityQueue { private ArrayList<BinaryTree> data;//  private int nElems;//-    public PriorityQueue() { data = new ArrayList<BinaryTree>(); nElems = 0; } public void insert(BinaryTree newTree) {// if (nElems == 0) data.add(newTree); else { for (int i = 0; i < nElems; i++) { if (data.get(i).getFrequence() > newTree.getFrequence()) {//     data.add(i, newTree);// . ,  c       1  break;//       } if (i == nElems - 1) data.add(newTree); } } nElems++;// -   1 } public BinaryTree remove() {//   BinaryTree tmp = data.get(0);//   data.remove(0);//,  nElems--;// -   1 return tmp;//  (   ) } } 

الفئة التي تنشئ شجرة هوفمان:

 public class HuffmanTree { private final byte ENCODING_TABLE_SIZE = 127;//   private String myString;// private BinaryTree huffmanTree;//  private int[] freqArray;//  private String[] encodingArray;//  //----------------constructor---------------------- public HuffmanTree(String newString) { myString = newString; freqArray = new int[ENCODING_TABLE_SIZE]; fillFrequenceArray(); huffmanTree = getHuffmanTree(); encodingArray = new String[ENCODING_TABLE_SIZE]; fillEncodingArray(huffmanTree.getRoot(), "", ""); } //--------------------frequence array------------------------ private void fillFrequenceArray() { for (int i = 0; i < myString.length(); i++) { freqArray[(int)myString.charAt(i)]++; } } public int[] getFrequenceArray() { return freqArray; } //------------------------huffman tree creation------------------ private BinaryTree getHuffmanTree() { PriorityQueue pq = new PriorityQueue(); //   for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) {//     Node newNode = new Node((char) i, freqArray[i]);//    Node BinaryTree newTree = new BinaryTree(newNode);//  Node  BinaryTree pq.insert(newTree);//   } } while (true) { BinaryTree tree1 = pq.remove();//    . try { BinaryTree tree2 = pq.remove();//     Node newNode = new Node();//  Node newNode.addChild(tree1.getRoot());//      newNode.addChild(tree2.getRoot()); pq.insert(new BinaryTree(newNode); } catch (IndexOutOfBoundsException e) {//     return tree1; } } } public BinaryTree getTree() { return huffmanTree; } //-------------------encoding array------------------ void fillEncodingArray(Node node, String codeBefore, String direction) {//   if (node.isLeaf()) { encodingArray[(int)node.getLetter()] = codeBefore + direction; } else { fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0"); fillEncodingArray(node.getRightChild(), codeBefore + direction, "1"); } } String[] getEncodingArray() { return encodingArray; } public void displayEncodingArray() {//  fillEncodingArray(huffmanTree.getRoot(), "", ""); System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); } } System.out.println("========================================================"); } //----------------------------------------------------- String getOriginalString() { return myString; } } 

الفئة التي تحتوي على الترميز / فك التشفير:

 public class HuffmanOperator { private final byte ENCODING_TABLE_SIZE = 127;//  private HuffmanTree mainHuffmanTree;//  (   ) private String myString;//  private int[] freqArray;//  private String[] encodingArray;//  private double ratio;//  public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress this.mainHuffmanTree = MainHuffmanTree; myString = mainHuffmanTree.getOriginalString(); encodingArray = mainHuffmanTree.getEncodingArray(); freqArray = mainHuffmanTree.getFrequenceArray(); } public HuffmanOperator() {}//for extract; //---------------------------------------compression----------------------------------------------------------- private String getCompressedString() { String compressed = ""; String intermidiate = "";// (  ) //System.out.println("=============================Compression======================="); //displayEncodingArray(); for (int i = 0; i < myString.length(); i++) { intermidiate += encodingArray[myString.charAt(i)]; } //      .       8=> //    ( 1,  ) byte counter = 0;//     (   : 0<=counter<8<127) for (int length = intermidiate.length(), delta = 8 - length % 8; counter < delta ; counter++) {//delta -    intermidiate += "0"; } // -         compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate; //  setCompressionRatio(); //System.out.println("==============================================================="); return compressed; } private void setCompressionRatio() {//   double sumA = 0, sumB = 0;//A-the original sum for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { sumA += 8 * freqArray[i]; sumB += encodingArray[i].length() * freqArray[i]; } } ratio = sumA / sumB; } public byte[] getBytedMsg() {//final compression StringBuilder compressedString = new StringBuilder(getCompressedString()); byte[] compressedBytes = new byte[compressedString.length() / 8]; for (int i = 0; i < compressedBytes.length; i++) { compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2); } return compressedBytes; } //---------------------------------------end of compression---------------------------------------------------------------- //------------------------------------------------------------extract----------------------------------------------------- public String extract(String compressed, String[] newEncodingArray) { String decompressed = ""; String current = ""; String delta = ""; encodingArray = newEncodingArray; //displayEncodingArray(); // -   for (int i = 0; i < 8; i++) delta += compressed.charAt(i); int ADDED_ZEROES = Integer.parseInt(delta, 2); for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) { //i = 8, ..      -   current += compressed.charAt(i); for (int j = 0; j < ENCODING_TABLE_SIZE; j++) { if (current.equals(encodingArray[j])) {//  decompressed += (char)j;//   current = "";//    } } } return decompressed; } public String getEncodingTable() { String enc = ""; for (int i = 0; i < encodingArray.length; i++) { if (freqArray[i] != 0) enc += (char)i + encodingArray[i] + '\n'; } return enc; } public double getCompressionRatio() { return ratio; } public void displayEncodingArray() {//  System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { //if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); //} } System.out.println("========================================================"); } } 

الفصل الذي يسهل الكتابة إلى ملف:

 import java.io.File; import java.io.PrintWriter; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.Closeable; public class FileOutputHelper implements Closeable { private File outputFile; private FileOutputStream fileOutputStream; public FileOutputHelper(File file) throws FileNotFoundException { outputFile = file; fileOutputStream = new FileOutputStream(outputFile); } public void writeByte(byte msg) throws IOException { fileOutputStream.write(msg); } public void writeBytes(byte[] msg) throws IOException { fileOutputStream.write(msg); } public void writeString(String msg) { try (PrintWriter pw = new PrintWriter(outputFile)) { pw.write(msg); } catch (FileNotFoundException e) { System.out.println(" ,     !"); } } @Override public void close() throws IOException { fileOutputStream.close(); } public void finalize() throws IOException { close(); } } 

الفصل الذي يسهل القراءة من ملف:

 import java.io.FileInputStream; import java.io.EOFException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.Closeable; import java.io.File; import java.io.IOException; public class FileInputHelper implements Closeable { private FileInputStream fileInputStream; private BufferedReader fileBufferedReader; public FileInputHelper(File file) throws IOException { fileInputStream = new FileInputStream(file); fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream)); } public byte readByte() throws IOException { int cur = fileInputStream.read(); if (cur == -1)//   throw new EOFException(); return (byte)cur; } public String readLine() throws IOException { return fileBufferedReader.readLine(); } @Override public void close() throws IOException{ fileInputStream.close(); } } 

حسنا ، والفئة الرئيسية:

 import java.io.File; import java.nio.charset.MalformedInputException; import java.io.FileNotFoundException; import java.io.IOException; import java.nio.file.Files; import java.nio.file.NoSuchFileException; import java.nio.file.Paths; import java.util.List; import java.io.EOFException; public class Main { private static final byte ENCODING_TABLE_SIZE = 127; public static void main(String[] args) throws IOException { try {//       if (args[0].equals("--compress") || args[0].equals("-c")) compress(args[1]); else if ((args[0].equals("--extract") || args[0].equals("-x")) && (args[2].equals("--table") || args[2].equals("-t"))) { extract(args[1], args[3]); } else throw new IllegalArgumentException(); } catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) { System.out.println("    "); System.out.println(" Readme.txt"); e.printStackTrace(); } } public static void compress(String stringPath) throws IOException { List<String> stringList; File inputFile = new File(stringPath); String s = ""; File compressedFile, table; try { stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath())); } catch (NoSuchFileException e) { System.out.println(" ,     !"); return; } catch (MalformedInputException e) { System.out.println("    "); return; } for (String item : stringList) { s += item; s += '\n'; } HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s)); compressedFile = new File(inputFile.getAbsolutePath() + ".cpr"); compressedFile.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) { fo.writeBytes(operator.getBytedMsg()); } //create file with encoding table: table = new File(inputFile.getAbsolutePath() + ".table.txt"); table.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(table)) { fo.writeString(operator.getEncodingTable()); } System.out.println("   : " + compressedFile.getAbsolutePath()); System.out.println("    " + table.getAbsolutePath()); System.out.println("     !"); double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//  double realRatio = Math.round((double) inputFile.length() / ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//  System.out.println("    " + idealRatio); System.out.println("      " + realRatio); } public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException { HuffmanOperator operator = new HuffmanOperator(); File compressedFile = new File(filePath), tableFile = new File(tablePath), extractedFile = new File(filePath + ".xtr"); String compressed = ""; String[] encodingArray = new String[ENCODING_TABLE_SIZE]; //read compressed file //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here: try (FileInputHelper fi = new FileInputHelper(compressedFile)) { byte b; while (true) { b = fi.readByte();//method returns EOFException compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0"); } } catch (EOFException e) { } //-------------------- //read encoding table: try (FileInputHelper fi = new FileInputHelper(tableFile)) { fi.readLine();//skip first empty string encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n' while (true) { String s = fi.readLine(); if (s == null) throw new EOFException(); encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length()); } } catch (EOFException ignore) {} extractedFile.createNewFile(); //extract: try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) { fo.writeString(operator.extract(compressed, encodingArray)); } System.out.println("    " + extractedFile.getAbsolutePath()); } } 

ملف التعليمات readme.txt متروك لك لكتابة نفسك :-)

الخاتمة

ربما هذا هو كل ما أردت قوله. إذا كان لديك ما تقوله حول عدم كفاءة التحسينات في الشفرة والخوارزمية وأي تحسين بشكل عام ، فلا تتردد في الكتابة. إذا أسأت فهم شيء ما ، فاكتب أيضًا. سأكون سعيداً أن أسمع منك في التعليقات!

PS

نعم ، نعم ، ما زلت هنا ، لأنني لم أنس معاملته. بالنسبة للسلسلة s1 ، يزن جدول الترميز 48 بايت - أكثر بكثير من الملف الأصلي ، ولم ينسوا أي أصفار إضافية (عدد الأصفار المضافة 7) => ستكون نسبة الضغط أقل من واحدة: 176 / (65 + 48 * 8 + 7) = 0.38. إذا لاحظت هذا أيضًا ، فأنت لست جيدًا في وجهك . نعم ، سيكون هذا التطبيق غير فعال للغاية بالنسبة للملفات الصغيرة. ولكن ماذا يحدث للملفات الكبيرة؟ تتجاوز أحجام الملفات حجم جدول الترميز. هنا الخوارزمية تعمل كما ينبغي! على سبيل المثال ، بالنسبة إلى المونولوج Faust ، يعطي أرشيف الأرشيف معاملًا حقيقيًا (غير مثالي) يساوي 1.46 - مرة واحدة ونصف تقريبًا! ونعم ، كان من المفترض أن يكون الملف باللغة الإنجليزية.