كتابة XGBoost من الصفر - الجزء 1: الأشجار القرار

مرحبا يا هبر!

بعد العديد من عمليات البحث عن أدلة عالية الجودة حول أشجار القرارات وخوارزميات المجموعات (التعزيز ، مجموعة القرارات ، إلخ) من خلال تنفيذها المباشر بلغات البرمجة ، وبدون العثور على أي شيء (من وجدها ، اكتب في التعليقات ، ربما سأتعلم شيئًا جديدًا) ، قررت أن أقود قيادتي الخاصة ، كما أرغب في رؤيتها. المهمة في الكلمات بسيطة ، ولكن كما تعلمون ، فإن الشيطان يكمن في الأشياء الصغيرة ، والتي يوجد بها الكثير من الخوارزميات مع الأشجار.

نظرًا لأن الموضوع واسع للغاية ، فسيكون من الصعب للغاية وضع كل شيء في مقال واحد ، لذلك سيكون هناك منشوران: الأول مخصص للأشجار ، وسيتم تخصيص الجزء الثاني لتنفيذ خوارزمية التدرج المعزز. يتم تجميع جميع المواد المعروضة هنا وتصميمها استنادًا إلى المصادر المفتوحة ورمزي ورمز الزملاء والأصدقاء. أحذرك على الفور ، سيكون هناك الكثير من التعليمات البرمجية.



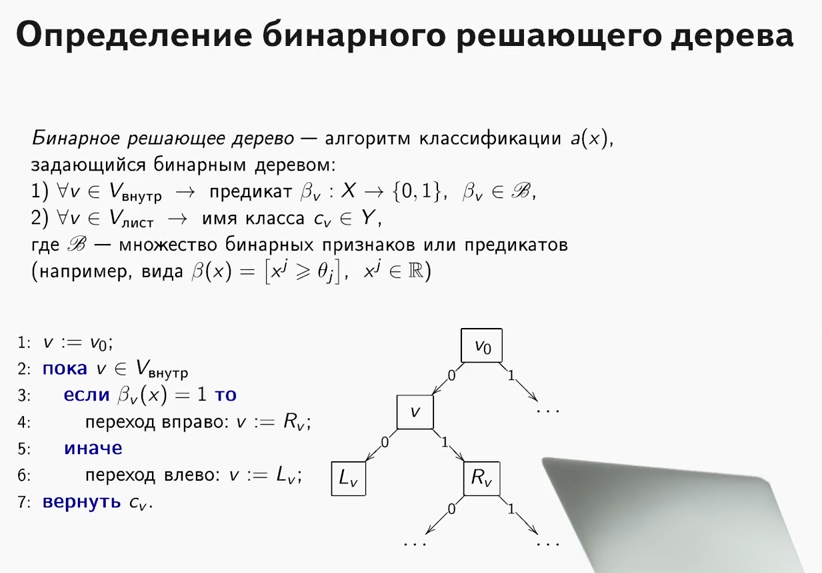
فما الذي تحتاج إلى معرفته وتكون قادرًا على تعلم كيفية كتابة خوارزميات المجموعات الخاصة بك مع أشجار القرار من الصفر؟ نظرًا لأن مجموعة الخوارزميات ليست أكثر من تكوين "خوارزميات ضعيفة" ، فإن كتابة مجموعة جيدة تتطلب "خوارزميات ضعيفة" جيدة ، وسنقوم بتحليلها بالتفصيل في هذه المقالة. كما يوحي الاسم ، فهذه أشجار مهمة ، وتتحول من بسيطة إلى معقدة ، وسوف نتعلم كيفية كتابتها. في هذه الحالة ، سيتم التركيز بشكل مباشر على التنفيذ ، وسيتم تقديم النظرية بأكملها كحد أدنى ، وسأقدم أساسًا روابط لمواد للدراسة المستقلة.

لمعرفة المواد ، تحتاج إلى فهم مدى خوارزمية لدينا جيدة أو سيئة. سوف نفهم ببساطة شديدة - سنصلح مجموعة من البيانات المحددة وسنقارن خوارزمياتنا بخوارزميات الأشجار من سكليرن (حسناً ، ما يمكن أن يحدث بدون هذه المكتبة). سنقارن الكثير: تعقيد الخوارزمية ، مقاييس البيانات ، مدة التشغيل ، إلخ.

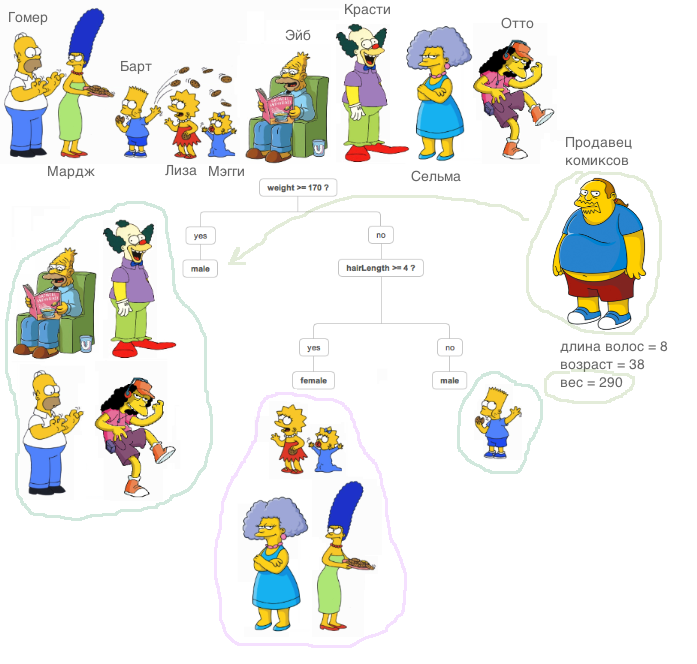
ما هي شجرة حاسمة؟ توجد مادة جيدة جدًا ، حيث يتم شرح مبدأ شجرة القرار ، في دورة نظام الوثائق الرسمية (بالمناسبة ، دورة رائعة ، أوصي لأولئك الذين يبدأون بالتعارف مع ML).

شرح مهم للغاية: في جميع الحالات الموضحة أدناه ، ستكون جميع العلامات حقيقية ، ولن نقوم بتحويلات خاصة مع بيانات خارج الخوارزميات (نقارن الخوارزميات ، وليس مجموعات البيانات).

الآن دعونا نتعلم كيفية حل مشكلة الانحدار باستخدام أشجار القرار. سوف نستخدم مقياس MSE كإنتروبيا.

نحن ننفذ فئة RegressionTree بسيطة للغاية ، والتي تعتمد على أسلوب تكراري. عن عمد ، نبدأ بتطبيق غير فعال للغاية ، لكن من السهل فهمه ، حتى نتمكن من تحسينه في المستقبل.

1. الفئة RegressionTree ()

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

سأشرح باختصار ما تفعله كل طريقة هنا.

طريقة fit ، كما يوحي الاسم ، تدرس النموذج. يتم تطبيق عينة التدريب على المدخلات ويتم إجراء تدريب على الأشجار. فرز العلامات ، نحن نبحث عن أفضل قسم للشجرة من حيث الحد من الانتروبيا ، في هذه الحالة mse . لتحديد أنه كان من الممكن العثور على انقسام جيد أمر بسيط للغاية ، يكفي تحقيق شرطين. لا نريد أن تندرج بعض الكائنات في القسم (الحماية من إعادة التدريب) ، ويجب أن يكون متوسط ​​الخطأ الخاص بـ mse أقل من الخطأ الموجود الآن في الشجرة - نحن نبحث عن نفس المكسب في الحصول على المعلومات . بعد الاطلاع على جميع العلامات وكل القيم الفريدة بهذه الطريقة ، سنتعرف على جميع الخيارات ونختار القسم الأفضل. ثم نقوم بإجراء مكالمة متكررة على الأقسام المستلمة حتى يتم استيفاء شروط الخروج من العودية.

أسلوب __predict ، كما يوحي الاسم ، يجعل المسند. بعد تلقي كائن كمدخل ، يمر عبر العقد الخاصة بالشجرة الناتجة - في كل عقدة ، يتم تثبيت رقم السمة والقيمة عليها ، واعتمادًا على القيمة التي تستخدمها الطريقة الواردة للكائن لهذه السمة ، نذهب إما إلى السليل الأيمن أو إلى اليسار ، حتى نصل إلى الورقة ، والتي سيكون هناك إجابة لهذا الكائن.

طريقة predict تفعل نفس الطريقة السابقة ، فقط لمجموعة من الكائنات.

نحن نستورد مجموعة بيانات كاليفورنيا الرئيسية المعروفة. هذه مجموعة بيانات منتظمة تحتوي على بيانات وهدف لحل مشكلة الانحدار.

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

حسنًا ، لنبدأ المقارنة! أولاً ، دعونا نرى مدى سرعة تعلم الخوارزمية. وضعنا في Sklearn وأنفسنا المعلمة max_depth الوحيدة ، max_depth تساوي 2.

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

سيتم عرض ما يلي:

• بالنسبة إلى الخوارزمية الخاصة بنا - أوقات وحدة المعالجة المركزية (CPU): المستخدم 4 دقائق و 47 ثانية ، SYS: 8.25 مللي ثانية ، المجموع: 4 دقائق و 47 ثانية
  الوقت الجدار: 4min 47s
• لأوقات Sklearn - CPU: المستخدم 53.5 مللي ثانية ، sys: 0 ns ، الإجمالي: 53.5 مللي ثانية
  وقت الجدار: 53.4 مللي ثانية

كما ترون ، الخوارزمية تتعلم آلاف المرات أبطأ. ما السبب؟ هيا بنا

تذكر كيف يتم ترتيب الإجراء الخاص بالعثور على أفضل قسم. كما تعلمون ، في الحالة العامة ، مع حجم الكائنات $$$N$ ومع عدد العلامات $$$د$ ، صعوبة العثور على أفضل الانقسام $$$O (N * logN * d)$ .

من أين يأتي هذا التعقيد؟

أولاً ، لإعادة حساب الخطأ بشكل فعال ، من الضروري فرز جميع الأعمدة من أجل الانتقال من الأصغر إلى الأكبر قبل المرور بالسمة. كما نفعل هذا لكل سمة ، وهذا يخلق تعقيد المقابلة. كما ترون ، نقوم بفرز العلامات ، لكن المشكلة تكمن في إعادة حساب الخطأ - في كل مرة نقوم فيها mse البيانات إلى طريقة mse ، والتي تعمل مع الخط. هذا يجعل خطأ إعادة فرز الأصوات غير فعالة للغاية! بعد كل شيء ، ثم صعوبة العثور على انقسام يزيد ل $$$O (N ^ 2 * d)$ لالكبير $$$N$ يبطئ بشكل كبير الخوارزمية. لذلك ، ننتقل بسلاسة إلى العنصر التالي.

2. فئة RegressionTree () مع إعادة فرز الأخطاء السريعة

ما يجب القيام به لإعادة سرد الخطأ بسرعة؟ خذ قلمًا وورقًا ، ورسم كيف ينبغي لنا تغيير الصيغ.

لنفترض في بعض الخطوات وجود خطأ محسوب بالفعل $$$N$ الأشياء. لديها الصيغة التالية: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$ . هنا لا بد من تقسيم $$$N$ ولكن الآن دعنا نتجاهل ذلك. نريد الحصول بسرعة على هذا الخطأ - $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2$ ، هذا هو ، رمي الخطأ الذي يقدمه العنصر $$$y_i$ إلى جزء آخر.

نظرًا لأننا نلقي الكائن ، يجب إعادة سرد الخطأ في مكانين - على الجانب الأيمن (باستثناء هذا الكائن) ، وعلى الجانب الأيسر (مع مراعاة هذا الكائن). لكن بدون فقدان العمومية ، سنستنتج صيغة واحدة فقط ، لأنها ستكون متشابهة.

نظرًا لأننا نعمل مع mse ، فقد كنا محظوظين: من الصعب إلى حد ما الحصول على إعادة فرز سريعة لخطأ ما ، ولكن عند العمل مع مقاييس أخرى (على سبيل المثال ، معيار Gini ، إذا قمنا بحل مشكلة التصنيف) ، فإن إعادة الفرز السريع أسهل بكثير.

حسنًا ، لنبدأ في اشتقاق الصيغ!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

سنكتب العضو الأول:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac { Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1 } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - 2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_N - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - \\ - (\ frac {y_N - y_i} { N}) ^ 2)$$

لاف ، فقط اليسار قليلاً. يبقى فقط للتعبير عن المبلغ المطلوب.

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) (\ frac {y_N - y_i} {N}) - (\ frac {y_N - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {y_i} {N}) ^ 2 دولا$$

ثم أصبح من الواضح كيفية التعبير عن المبلغ المرغوب. لإعادة حساب الخطأ ، نحتاج فقط إلى تخزين مجموع العناصر على اليمين واليسار ، وكذلك العنصر الجديد نفسه ، الذي وصل إلى الإدخال. الآن يتم سرد الخطأ ل $$$O (1)$ .

حسنًا ، دعنا ننفذ هذا في الكود.

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

دعونا نقيس الوقت الذي يقضيه الآن في التدريب ، ومقارنة مع التناظرية من Sklearn.

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• بالنسبة إلى الخوارزمية الخاصة بنا ، نحصل على - أوقات وحدة المعالجة المركزية: المستخدم 3.11 ثانية ، الأنظمة: 2.7 مللي ثانية ، الإجمالي: 3.11 ثانية
  وقت الجدار: 3.11 ثانية.
• بالنسبة إلى الخوارزمية من Sklearn - أوقات وحدة المعالجة المركزية: المستخدم 45.9 مللي ثانية ، sys: 1.09 مللي ثانية ، الإجمالي: 47 مللي ثانية
  وقت الجدار: 45.7 مللي ثانية.

النتائج بالفعل أكثر متعة. حسنًا ، دعنا نحسن الخوارزمية.

3. فئة RegressionTree () مع مجموعات خطية من الميزات

الآن ، في الخوارزمية الخاصة بنا ، لا يتم استخدام العلاقات بين السمات بأي طريقة. نصلح ميزة واحدة وننظر فقط إلى أقسام الفضاء المتعامدة. كيف تتعلم كيفية استخدام العلاقات الخطية بين السمات؟ وهذا هو ، للبحث عن أفضل أقسام ليست مثل $$$a_ {feat} <x$ و $$$\ sum_ {i = 1} ^ K b_i * a_i <x$ اين $$$K$ - هل الرقم أقل من بُعد فضاءنا؟

هناك العديد من الخيارات ، سأبرز اثنين من أكثر الخيارات إثارة للاهتمام من وجهة نظري. تم وصف كلا الطريقتين في كتاب فريدمان (اخترع هذه الأشجار).

سأقدم صورة حتى يكون واضحا المقصود منها:



أولاً ، يمكنك محاولة العثور على هذه الأقسام الخطية حسابيًا. من الواضح أنه من المستحيل فرز جميع المجموعات الخطية ، لأن هناك عددًا لا حصر له من المجموعات ، لذلك يجب أن تكون هذه الخوارزمية جشعة ، أي في كل تكرار ، تحسن نتيجة التكرار السابق. يمكن قراءة الفكرة الرئيسية لهذه الخوارزمية في الكتاب ، وسأترك أيضًا رابطًا هنا إلى مستودع صديقي وزميلي مع تنفيذ هذه الخوارزمية.

ثانياً ، إذا لم نبتعد عن فكرة العثور على أفضل قسم متعامد ، فكيف يمكننا تعديل مجموعة البيانات بحيث يتم استخدام المعلومات المتعلقة بعلاقة الميزات ويستند البحث إلى أقسام متعامدة؟ هذا صحيح ، لتحويل نوع من الميزات الأصلية إلى ميزات جديدة. على سبيل المثال ، يمكنك جمع مجموع من الميزات والبحث عن أقسام بها بالفعل. تتناسب هذه الطريقة مع مفهوم الخوارزمية ، ولكنها تؤدي مهمتها - فهي تبحث عن أقسام متعامدة موجودة بالفعل في نوع من الترابط بين السمات.

حسنًا ، دعنا ننفذها - سنضيف ميزات جديدة ، على سبيل المثال ، جميع أنواع مجموعات من ميزات الميزات $$$i، j$ اين $$$I <j$ . ألاحظ أن تعقيد الخوارزمية في هذه الحالة سيزداد ، فمن الواضح كم مرة. حسنًا ، لكي يتم النظر بشكل أسرع ، سوف نستخدم cython.

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. مقارنة النتائج

حسنًا ، دعنا نقارن النتائج. سنقارن ثلاث خوارزميات بنفس المعلمات - شجرة من سكليرن ، وشجرتنا العادية وشجرتنا بميزات جديدة. سنقوم بتقسيم مجموعة البيانات الخاصة بنا إلى مجموعات تدريب واختبار عدة مرات ، وحساب الخطأ.

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

الآن لنقم بتشغيل جميع الخوارزميات.

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

النتائج:



فقدت الشجرة العادية لدينا بسبب Sklearn (وهذا أمر مفهوم: Sklearn محسّن بشكل جيد ، وهي تستخدم بشكل افتراضي الكثير من المعلمات في الشجرة التي لا نأخذها في الاعتبار) ، ولكن عند إضافة كميات ، تصبح النتيجة أكثر متعة.

لتلخيص: تعلمنا كيفية كتابة الأشجار الحاسمة من نقطة الصفر ، وتعلمنا كيفية تحسين أدائها واختبار فعاليتها على مجموعات البيانات الحقيقية من خلال مقارنتها مع الخوارزمية من سكليرن. ومع ذلك ، فإن الطرق المقدمة هنا لا تحد من تحسين الخوارزميات ، لذلك ضع في اعتبارك أنه يمكن جعل الشفرة المقترحة أفضل. في المقالة التالية ، سنكتب تعزيز بناءً على هذه الخوارزميات.

كل النجاح!