كتابة XGBoost من نقطة الصفر - الجزء 2: زيادة التدرج

مرحبا بالجميع!

في المقالة الأخيرة ، اكتشفنا كيف يتم ترتيب الأشجار القرار ، ومن الصفر نفذنا
خوارزمية البناء ، في وقت واحد تحسين وتحسينه. في هذه المقالة ، سننفذ خوارزمية تعزيز التدرج ، وفي النهاية سننشئ XGBoost الخاص بنا. سيتبع السرد نفس النمط: نكتب خوارزمية ونصفها ونلخصها بمقارنة نتائج العمل مع نظائرها من سكليرن.

في هذه المقالة ، سيتم التركيز أيضًا على التطبيق في الكود ، لذلك من الأفضل قراءة النظرية بأكملها في أخرى معًا (على سبيل المثال ، في دورة ODS ) ، وبالفعل مع العلم بالنظرية ، يمكنك المتابعة إلى هذه المقالة ، لأن الموضوع معقد للغاية.



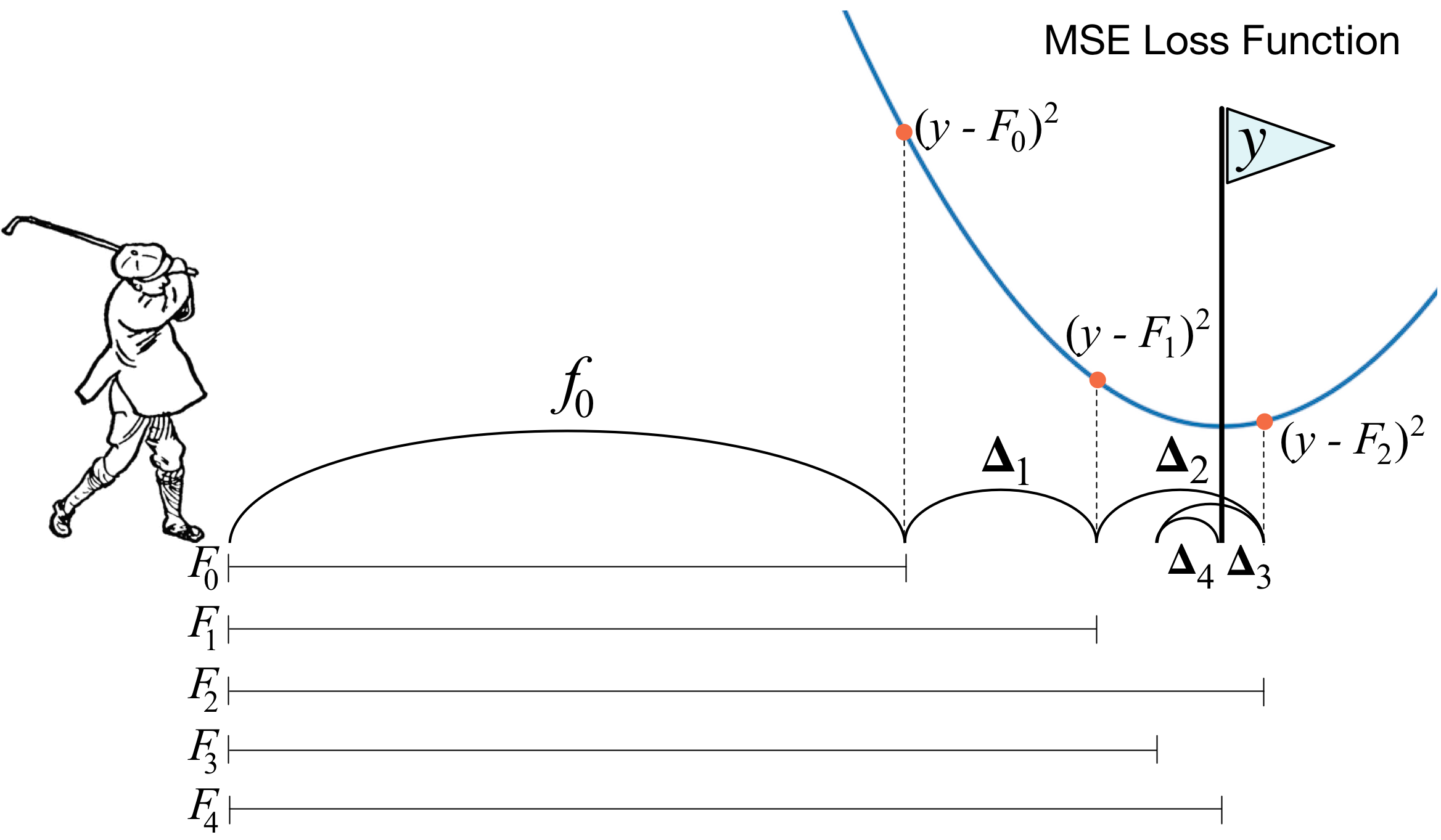
ما هو تعزيز التدرج؟ تصف صورة لاعب الجولف الفكرة الرئيسية تمامًا. من أجل دفع الكرة داخل الحفرة ، يقوم اللاعب بأداء كل ضربة تالية مع مراعاة تجربة السكتات الدماغية السابقة - بالنسبة له يعتبر هذا شرطًا ضروريًا لوضع الكرة في الحفرة. إذا كان الأمر وقحًا جدًا (لست سيدًا للجولف :)) ، فمع كل ضربة جديدة ، أول شيء ينظر إليه لاعب الجولف هو المسافة بين الكرة والثقب بعد الضربة السابقة. والمهمة الرئيسية هي تقليل هذه المسافة من خلال الضربة التالية.

تم بناء Boosting بطريقة مشابهة جدًا. أولاً ، نحتاج إلى تقديم تعريف "الحفرة" ، أي الهدف الذي سنسعى إليه. ثانياً ، نحتاج أن نتعلم فهم أي جانب نحتاج للتغلب عليه مع النادي من أجل الاقتراب من الهدف. ثالثًا ، مع أخذ كل هذه القواعد في الاعتبار ، تحتاج إلى الخروج بالتسلسل الصحيح للسكتات الدماغية بحيث يقلل كل منها لاحق المسافة بين الكرة والثقب.

الآن نعطي تعريف أكثر صرامة قليلاً. نقدم نموذج التصويت المرجح:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i ، x \ in X ، b_i \ in R$$

هنا $$$X$ هو الفضاء الذي نأخذ منه الأشياء ، $$$b_i ، a_i$ - هذا هو المعامل أمام النموذج والنموذج نفسه ، أي شجرة القرار. لنفترض أنه بالفعل في مرحلة ما ، باستخدام القواعد الموضحة ، كان من الممكن إضافة إلى التكوين $$ خوارزمية ضعيفة. لمعرفة كيفية فهم نوع الخوارزمية التي يجب أن تكون في الخطوة $$$T$ ، نحن نقدم وظيفة الخطأ:

$$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarrow min_ {a_T، b_T}$

اتضح أن أفضل الخوارزمية هي تلك التي يمكنها تقليل الخطأ الذي تم تلقيه في التكرارات السابقة. ونظرًا لأن التعزيز متدرج ، فيجب أن تحتوي وظيفة الخطأ هذه بالضرورة على متجه مضاد للتدرج يمكنك من خلاله البحث عن الحد الأدنى. هذا كل شئ!

قبل التنفيذ مباشرة ، سأضيف بضع كلمات حول كيفية ترتيب كل شيء معنا. كما في المقالة السابقة ، فإننا نعتبر MSE بمثابة خسارة. دعنا نحسب التدرج اللوني:

$$

$$mse (ذ ، التنبؤ) = (ذ - التنبؤ) ^ 2 \\ \ nabla_ {التنبؤ} mse (ذ ، التنبؤ) = التنبؤ - ذ$$

وبالتالي ، فإن ناقل antigradient سيكون مساويا ل $$$y - توقع$ . في الخطوة $$$i$ نحن نعتبر أخطاء الخوارزمية التي تم الحصول عليها في التكرارات السابقة. بعد ذلك ، نقوم بتدريب الخوارزمية الجديدة الخاصة بنا على هذه الأخطاء ، ثم نضيفها إلى مجموعتنا بعلامة ناقص وبعض المعاملات.

الآن لنبدأ.

1. تنفيذ التدرج المعتاد تعزيز الطبقة

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

سنقوم الآن ببناء منحنى الخسارة على مجموعة التدريب للتأكد من أن لدينا في كل تكرار انخفاض حقيقي.

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. التعبئة فوق الأشجار الحاسمة

حسنًا ، قبل أن نقارن النتائج ، دعونا نتحدث عن الإجراء الخاص بتعبئة الأشجار.

كل شيء بسيط هنا: نريد حماية أنفسنا من إعادة التدريب ، وبالتالي ، بمساعدة أخذ العينات مع العودة ، سنقوم بتقييم توقعاتنا حتى لا نواجه انبعاثات بطريق الخطأ (لماذا يعمل هذا - قراءة الرابط بشكل أفضل).

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

حسنًا ، الآن كخوارزمية أساسية ، لا يمكننا استخدام شجرة واحدة ، ولكننا نستخدمها في التعبئة من الأشجار - مرة أخرى ، سنحمي أنفسنا من إعادة التدريب.

3. النتائج

قارن نتائج خوارزمياتنا.

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

تلقى:



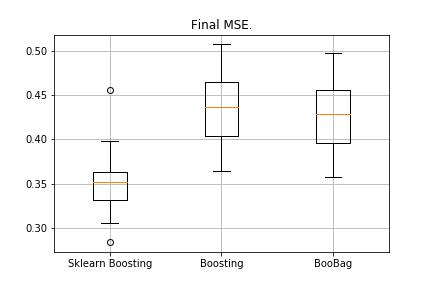
لا يمكننا بعد هزيمة التناظرية من سكليرن ، لأنه مرة أخرى لا نأخذ في الاعتبار الكثير من المعلمات المستخدمة في هذه الطريقة . ومع ذلك ، نرى أن التعبئة تساعد قليلاً.

دعونا لا تيأس ، وانتقل إلى كتابة XGBoost.

4. XGBoost

قبل قراءة المزيد ، أنصحك بشدة أولاً بالتعرف على الفيديو التالي ، والذي يشرح النظرية جيدًا.

أذكر ما الخطأ الذي قللناه في التعزيز الطبيعي:

$$

$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

يضيف XGBoost صراحة إلى وظيفة الخطأ هذه:

$$

$$err (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ {i = 1} ^ T \ أوميغا (a_i)$$

كيف تفكر في هذه الوظيفة؟ أولاً ، نقترب من ذلك بمساعدة سلسلة تايلور من الدرجة الثانية ، حيث تُعتبر الخوارزمية الجديدة بمثابة زيادة ننتقل إليها ، ثم نرسم بالفعل ، اعتمادًا على نوع الخسارة التي لدينا:

$$$f (x + \ delta x) \ thickapprox f (x) + f (x) '\ delta x + 0.5 * f (x)' '(\ delta x) ^ 2$

من الضروري تحديد الشجرة التي سنعتبرها سيئة وأيها جيدة.

أذكر ما هو مبدأ الانحدار الذي تم بناؤه $$$L_2 دولا$ -regularization - كلما كانت قيم المعاملات طبيعية قبل الانحدار ، كان الأسوأ ، لذلك ، يجب أن تكون أصغر ما يمكن.

في XGBoost ، الفكرة متشابهة للغاية: تغريم الشجرة إذا كان مجموع القيم في الأوراق فيها كبيرًا جدًا. لذلك ، يتم تقديم تعقيد الشجرة على النحو التالي:

$$

$$\ omega (a) = \ gamma Z + 0.5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$ - القيم في الأوراق ، $$$Z$ - عدد الأوراق.

هناك صيغ انتقال في الفيديو ، ولن نعرضها هنا. كل هذا يعود إلى حقيقة أننا سنختار قسمًا جديدًا ، مما يزيد من المكاسب:

$$

$$Gain = \ frac {G_l ^ 2} {S_l ^ 2 + \ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(G_l + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ gamma$$

هنا $$$\ gamma، \ lambda$ هي المعلمات العددية للتنظيم ، و $$$G_i ، S_i$ - المبالغ المقابلة للمشتقات الأولى والثانية لهذا القسم.

هذا كل شيء ، تم توضيح النظرية باختصار شديد ، يتم إعطاء الروابط ، والآن دعونا نتحدث عن ما ستكون المشتقات إذا كنا نعمل مع MSE. انها بسيطة:

$$$mse (ذ ، التنبؤ) = (ذ - التنبؤ) ^ 2 \\ \ nabla_ {التنبؤ} mse (ذ ، التنبؤ) = التنبؤ - y \\ \ nabla_ {التنبؤ} ^ 2 mse (ذ ، التنبؤ) = 1$

متى سنقوم بحساب المبلغ $$$G_i ، S_i$ ، فقط أضف إلى الأول $$ والثاني هو مجرد الكمية.

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

توضيح بسيط: لجعل الصيغ في الأشجار مع كسب أكثر جمالا ، في دفعة نحن ندرب الهدف مع علامة ناقص.

نقوم بتعديل طفيف لدينا تعزيز ، وجعل بعض المعلمات على التكيف. على سبيل المثال ، إذا لاحظنا أن الخسارة قد بدأت في الوصول إلى هضبة ، فإننا نخفض معدل التعلم ونزيد من الحد الأقصى للتقديرات التالية. سنضيف أيضًا حقائب جديدة - الآن سنعمل على زيادة حجم الحقيبة الشجرية مع تحقيق مكاسب:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. النتائج

حسب التقاليد ، نقارن النتائج:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

ستكون الصورة على النحو التالي:



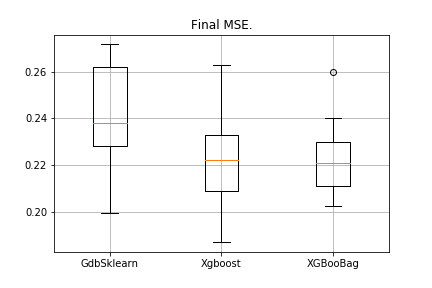
يحتوي XGBoost على أقل خطأ ، لكن XGBooBag لديه خطأ أكثر ازدحامًا ، وهو بالتأكيد أفضل: الخوارزمية أكثر استقرارًا.

هذا كل شيء. آمل حقًا أن تكون المادة المقدمة في مقالتين مفيدة ، ويمكنك أن تتعلم شيئًا جديدًا لنفسك. أعرب عن امتناني الخاص لديميتري للحصول على ملاحظات شاملة ورمز المصدر ، وعلى أنتون للحصول على المشورة ، وفلاديمير لمهام صعبة للدراسة.

كل النجاح!