كيف يعمل تصنيف الصفحات: التنفيذ في البحث عن طريق الجبر الخطي وطريقة القوة

مرحبا يا هابروفسك المواطنين!

اسمي اليكس هذه المرة أنا البث من مكان العمل في ITAR-TASS.

في هذا النص القصير ، سوف أعرض عليك طريقة حساب PageRank © (المشار إليها فيما يلي باسم PR) باستخدام أمثلة بسيطة مفهومة باللغة R. الخوارزمية هي ملكية فكرية لـ Google ، ولكن نظرًا لفائدتها في مهام تحليل البيانات ، يتم استخدام العديد من المهام ، والتي يمكن اختزالها للبحث عن العقد الكبيرة في الرسم البياني وتصنيفها حسب الأهمية.

ذكر شركة كبيرة في منشور ليس إعلانًا.

بما أنني لست عالم رياضيات محترفًا ، فإنني أستخدم هذا المقال وهذا البرنامج التعليمي كدليل وأوصي به.

فهم بديهي للعلاقات العامة

فهم كيف يعمل هذا ليس بالأمر الصعب. هناك مجموعة من العناصر المترابطة. إليكم مدى ارتباطهم بالتحديد - هذا سؤال واسع: ربما من خلال الروابط (مثل Google) ، وربما من خلال ذكر بعضهم البعض (نفس الروابط تقريبًا) ، يمكن أن تكون احتمالات الانتقال بين العناصر (مصفوفة عملية Markov) محددة مسبقًا دون تحديد المادي معنى التواصل. أود أن أسند إلى هذه العناصر معيارًا مهمًا للأهمية ، يحمل معلومات حول احتمال أن يزور هذا العنصر بعض الجسيمات المجردة التي تنتقل عبر الرسم البياني في عملية الانتشار.

أم ، هذا لا يبدو واضحا جدا. من الأسهل تخيل شخص يستخدم كمبيوتر محمول مع خشخاش ، ويتصفح صفحات نتائج البحث ، ويدخن الشيشة ، ويتبع الروابط من صفحة إلى أخرى ، وغالبًا ما يظهر على نفس الصفحة (أو الصفحات).

ويرجع ذلك إلى حقيقة أن بعض الصفحات التي يزورها تحتوي على مثل هذه المعلومات المثيرة للاهتمام في المصدر الأصلي والتي تضطر الصفحات الأخرى إلى إعادة طباعتها مع الإشارة إلى الارتباط.

مثل هذا الرجل في جوجل كان اسمه سيرفر عشوائي. إنه جسيم في عملية الانتشار: تغيير منفصل للموقف على الرسم البياني بمرور الوقت. والاحتمال الذي يزور به الصفحة مع وقت نشر يميل إلى ما لا نهاية هو العلاقات العامة.

تنفيذ بسيط لحساب العلاقات العامة

دعونا نتفق - نحن نعمل مع 10 عناصر ، في هذا الرسم البياني الصغير المريح.

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

يحتوي كل عنصر من العناصر (العقد) العشرة على 10 إلى 14 مرجعًا إلى عقد أخرى بترتيب عشوائي ، باستثناء نفسه. في الوقت الحالي ، نقرر فقط أن البيانات المذكورة هي رابط ويب.

من الواضح أنه قد يحدث أن يتم ذكر بعض العناصر أكثر من غيرها. تحقق من ذلك.

بالمناسبة ، أوصي باستخدام حزمة data.table للتجارب. بالتزامن مع مبادئ tidyverse ، كل شيء يتحول بكفاءة وبسرعة.

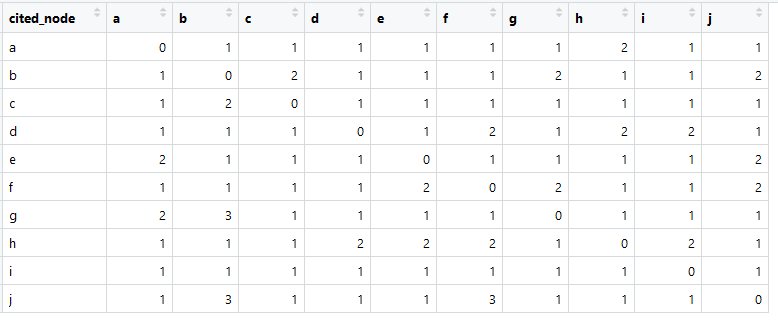
هذه هي الطريقة التي تبدو بها مصفوفة الارتباط الخاصة بنا (تسمى بالإنجليزية في معظم الأحيان باسم المصفوفة المجاورة).

المجموع في كل عمود أكبر من الصفر ، مما يعني وجود اتصال من كل عنصر مع بعض العناصر الأخرى (هذا مهم لمزيد من التحليل).

> تطبيق (dt [، - 1 ، مع = F] ، 2 ، المجموع)
abcdefghij
11 14 10 10 11 13 11 11 11 12

استنادًا إلى هذا الجدول ، يمكننا إنشاء مصفوفة تقارب ، أو ، في رأينا ، مصفوفة القرب (وتسمى أيضًا مصفوفة الانتقال) ، والتي يطلق عليها علماء الرياضيات المصفوفة العشوائية (المصفوفة العشوائية): المصدر الرئيسي

قم بتعيينه إلى متغير باسم A.



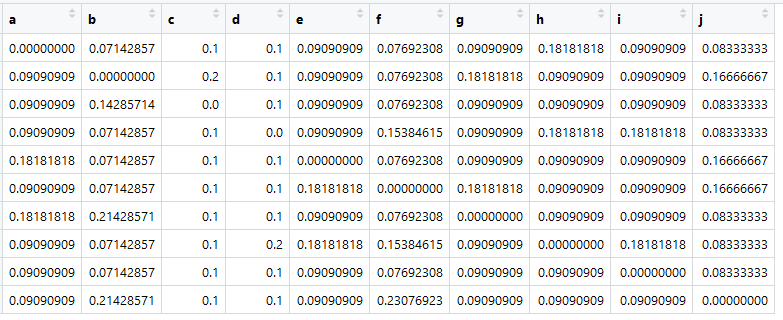
الشيء الأكثر أهمية الآن هو أن المجموع في جميع الأعمدة يساوي واحد.

> colSums (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1

ها هي - مصفوفة من التحولات ، إنها ماركوف ، إنها أوجه تشابه. الأشكال هي احتمالات الانتقال من عنصر في عمود إلى عنصر في صف واحد.

هذه ، بالطبع ، ليست "أوجه تشابه" حقيقية. الحاضر سيكون ، على سبيل المثال ، إذا قمنا بحساب جيب تمام الزاوية بين عرض المستندات. لكن من المهم أن يتم تقليل مصفوفة الانتقال إلى (شبه مستعارة) الاحتمالات بحيث يكون مجموع كل عمود مساويًا لكل عمود.

دعنا نلقي نظرة على الرسم البياني لماركوف (A):



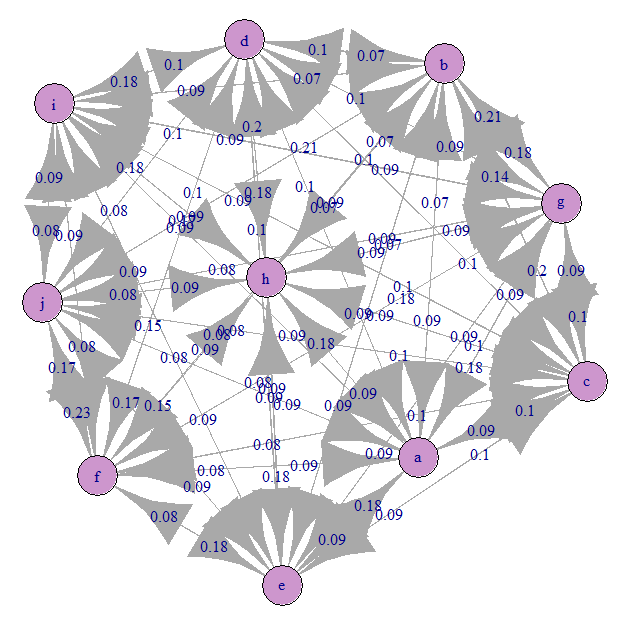
كل شيء مرتبك بالتساوي تقريبا). هذا لأننا حددنا التحولات equiprobable.

والآن حان الوقت للسحر!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

بالنسبة للمصفوفة العشوائية A ، يجب أن تكون القيمة الذاتية الأولى مساوية للوحدة ، ويكون المتجه الإلكتروني المقابل هو ناقل PageRank.

> طباعة (جولة (العلاقات العامة ، 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

هذا هو المتجه لقيم العلاقات العامة - وهذا هو المتغير الطبيعي لمصفوفة الانتقال A ، والذي يتوافق مع القيمة الذاتية لهذه المصفوفة المساوية للوحدة - المتجهات الذاتية المسيطرة.

الآن يمكنك ترتيب العناصر. ولكن نظرًا لخصائص التجربة ، فإن لها وزنًا مشابهًا للغاية.

المشاكل وحلولها باستخدام طريقة السلطة

قد لا تلبي مصفوفة الانتقال A شروط الاستوكاستك.

أولاً ، قد تكون هناك عناصر لا تشير إلى أي مكان ، أي مع عدم وجود ملاحظات (يمكن أن تشير إليها بنفسها). بالنسبة إلى الرسوم البيانية الحقيقية الكبيرة ، هذه مشكلة محتملة. هذا يعني أن أحد أعمدة المصفوفة سيكون به أصفار فقط. في هذه الحالة ، لن يعمل الحل من خلال المتغيرات الذاتية.

قامت Google بحل هذه المشكلة عن طريق ملء عمود بتوزيع احتمالي موحد p = 1 / N. حيث N هو عدد كل العناصر.

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

ثانياً ، قد يحتوي الرسم البياني على عناصر بها ملاحظات لبعضهم البعض ، ولكن لا تحتوي على العناصر المتبقية من الرسم البياني. هذه أيضًا مشكلة لا يمكن التغلب عليها للجبر الخطي بسبب انتهاك الافتراضات.

يتم حلها عن طريق إدخال ثابت يسمى عامل التخميد ، والذي يشير إلى احتمال مسبق للانتقال من أي عنصر إلى أي عنصر آخر ، حتى لو لم تكن هناك روابط مادية. بمعنى آخر ، الانتشار ممكن في أي ولاية.

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

إذا طبقنا هذه التحولات على المصفوفة الخاصة بنا ، فيمكن حلها مرة أخرى من خلال eigenvectors!

ثالثًا ، قد لا تكون المصفوفة المربعة مربعة ، لكن هذا أمر بالغ الأهمية! لن أتطرق في هذه اللحظة ، لأنني أعتقد أنك نفسك ستكتشف كيفية إصلاحها.

ولكن هناك طريقة أسرع وأكثر دقة ، وهي أيضًا أكثر اقتصادا في الذاكرة (والتي قد تكون ذات صلة برسوم بيانية كبيرة): طريقة الطاقة.

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

فويلا!

> طباعة (جولة (العلاقات العامة ، 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11
> طباعة (جولة (pr2 ، 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

على هذا سأنتهي البرنامج التعليمي. أتمنى أن تجدها مفيدة.

لقد نسيت أن أقول أنه لبناء مصفوفة من التحولات (الاحتمالات) ، يمكنك استخدام تشابه النصوص ، وعدد المراجع ، وحقيقة الارتباط ، والمقاييس الأخرى التي تؤدي إلى الاحتمالات الزائفة أو الاحتمالات. مثال مثير للاهتمام إلى حد ما هو ترتيب الجمل في النص على مصفوفة التشابه للكلمة bags tf-idf لتسليط الضوء على الجملة التي تلخص النص بأكمله. قد يكون هناك استخدامات مبتكرة أخرى للعلاقات العامة.

أوصي بتجربة اللعب بمصفوفة الانتقال والتأكد من حصولك على قيم علاقات عامة رائعة ، والتي يسهل تفسيرها أيضًا.

إذا رأيت معلومات غير دقيقة أو أخطاء معي - فذكر التعليقات أو الرسالة ، وسأقوم بتصحيح كل شيء.

يتم تجميع جميع الشفرات هنا:


ملاحظة: هذه الفكرة برمتها يتم تنفيذها بسهولة بلغات أخرى ، على الأقل في بيثون ، لقد فعلت كل شيء دون صعوبة.