جوليا وطريقة النسب المنسق

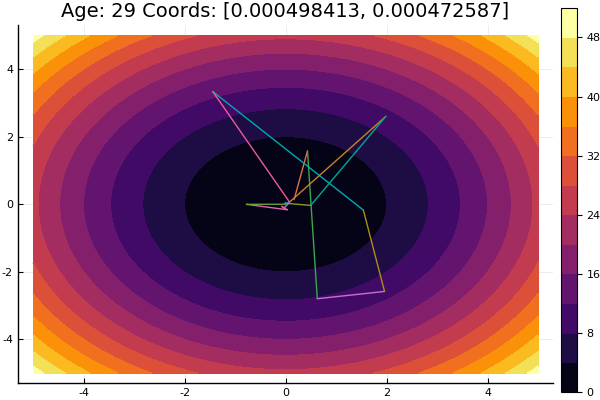
تعد طريقة الإحداثيات النسبية إحدى أبسط الطرق للتحسين متعدد الأبعاد وتقوم بعمل جيد للعثور على الحد الأدنى المحلي من الوظائف باستخدام طبوغرافيا سلسة نسبيًا ، لذلك من الأفضل أن تبدأ في التعرف على طرق التحسين منها.

يتم البحث عن الحد الأقصى في اتجاه محاور الإحداثيات ، أي أثناء عملية البحث ، يتم تغيير إحداثي واحد فقط. وبالتالي ، فإن مشكلة متعددة الأبعاد تقلل إلى مشكلة ذات بعد واحد.

خوارزمية

الدورة الأولى:

• $$$x_1 = var$ ، $$$x_2 = x_2 ^ 0$ ، $$$x_3 = x_3 ^ 0$ ، ... ، $$$x_n = x_n ^ 0$ .
• تبحث عن وظائف القصوى $$$f (x_1)$ . ضع أقصى وظيفة في هذه النقطة $$$x_1 ^ 1$ .
• $$$x_1 = x_1 ^ 1$ ، $$$x_2 = var$ ، $$$x_3 = x_3 ^ 0$ ، ... ، $$$x_n = x_n ^ 0$ . وظيفة القذف $$$f (x_2)$ يساوي $$$x_2 ^ 1$
• ...
• $$$x_1 = x_1 ^ 1$ ، $$$x_2 = x_2 ^ 1$ ، $$$x_3 = x_3 ^ 1$ ، ... ، $$$x_n = var$ .
  نتيجة لتنفيذ الخطوات n ، تم العثور على نقطة جديدة من النهج إلى الطرف $$$(x_1 ^ 1 ، x_2 ^ 1 ، ... ، x_n ^ 1)$ . بعد ذلك ، نتحقق من معيار نهاية الحساب: إذا تم الوفاء به ، فسيتم العثور على الحل ، وإلا فإننا نؤدي دورة أخرى.

التحضير

تحقق من إصدارات الحزمة:

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics 

نحدد وظيفة لرسم خطوط السطح أو المستوى التي سيكون من المناسب فيها ضبط حدود الرسم البياني:

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end 

كدالة نموذجية ، نختار مكافئ إهليلجي

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1]) 

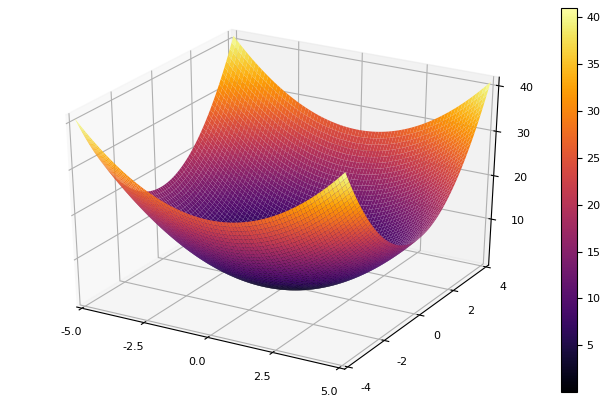
تنسيق النسب

نحن نطبق الطريقة في دالة تأخذ اسم طريقة التحسين أحادية البعد ، وأبعاد المشكلة ، والخطأ المطلوب ، والتقريب الأولي ، والقيود المفروضة على خطوط مستوى الرسم. يتم تعيين جميع المعلمات إلى القيم الافتراضية.

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end 

بعد ذلك ، سنحاول طرقًا مختلفة للتحسين أحادي البعد.

طريقة نيوتن

$$

$$x_ {n + 1} = x_n - \ frac {f (x_n)} {f '(x_n)}$$

فكرة الطريقة بسيطة مثل التنفيذ

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

يطلب نيوتن تقريبًا أوليًا ، وبدون حصر الخطوات ، يمكنه بسهولة ركوب مسافات غير معروفة. حساب المشتق أمر مرغوب فيه ، ولكن يمكن الاستغناء عن اختلاف بسيط. نقوم بتعديل وظيفتنا:

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

معكوس مكافئ الاستيفاء

طريقة لا تتطلب معرفة المشتق ولديها تقارب جيد

 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4]) 

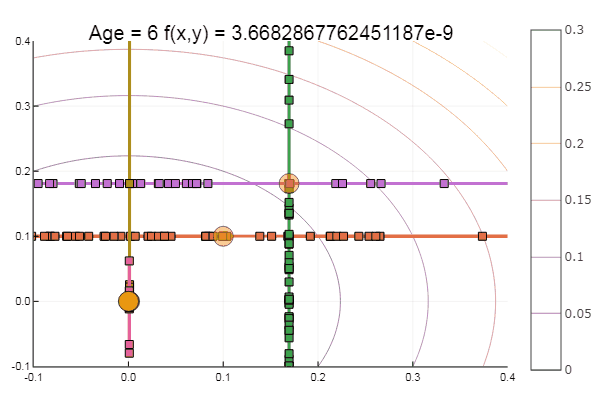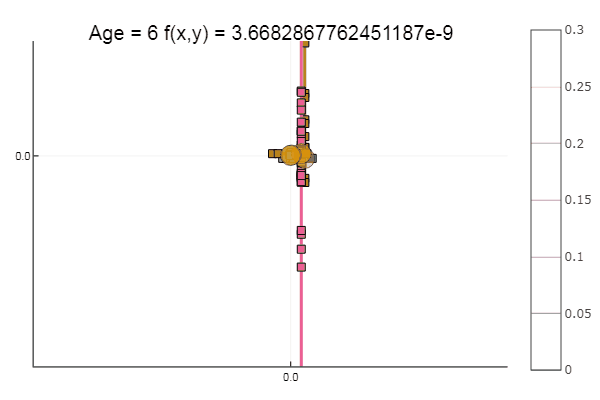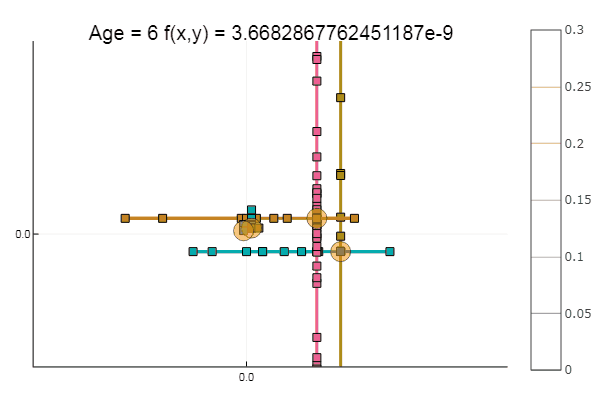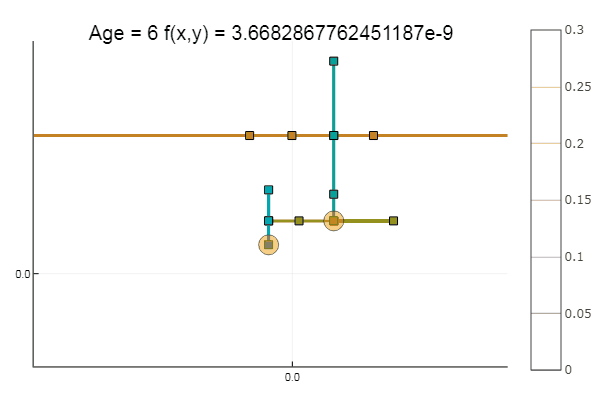
إذا أخذنا التقريب الأولي بشكل أسوأ ، فستبدأ الطريقة في المطالبة بعدد هائل من الخطوات لكل عصر من النسب الإحداثي. في هذا الصدد ، فاز شقيقه

مكافئ متسلسل الاستيفاء

يتطلب أيضًا ثلاث نقاط بداية ، لكن في العديد من وظائف الاختبار ، تظهر نتائج مرضية أكثر.

 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4]) 

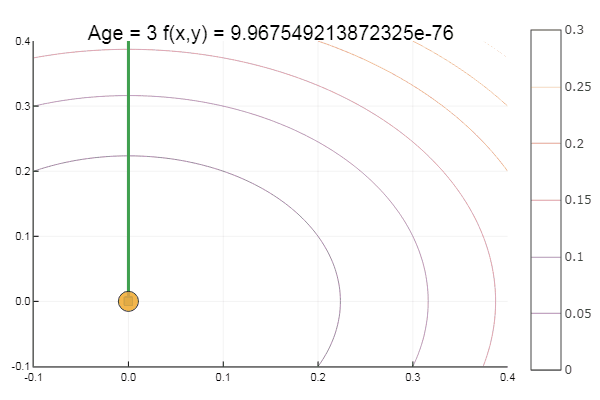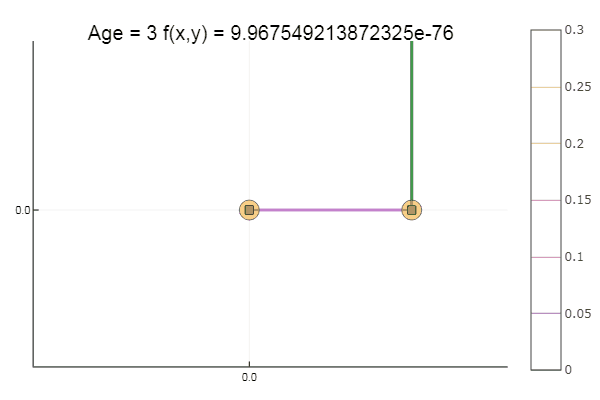
الخروج من نقطة بداية crappy جدا جاء في ثلاث خطوات! جيد ... لكن كل الطرق لها عيب - تتلاقى مع الحد الأدنى المحلي. الآن لنأخذ وظيفة أكلي للبحث

$$

$$f (x، y) = - 20 \ exp \ left [-0.2 {\ sqrt {0.5 \ left (x ^ {2} + y ^ {2} \ right)}} \ right] - \ exp \ left [ 0.5 \ left (\ cos 2 \ pi x + \ cos 2 \ pi y \ right) \ right] + e + 20$$

 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5]) 

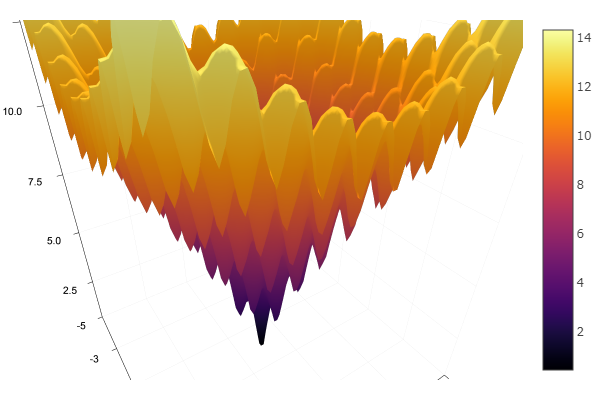
 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4]) 

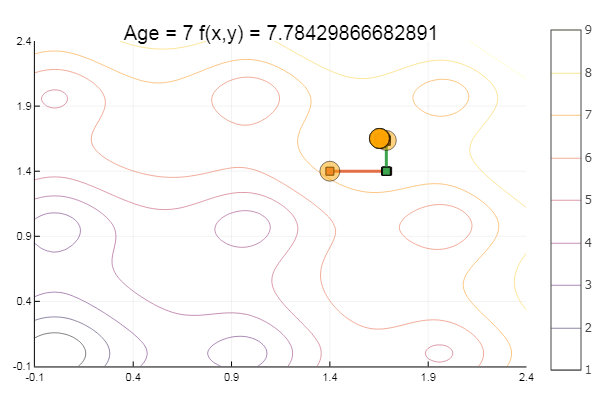
طريقة النسبة الذهبية

النظرية على الرغم من أن التنفيذ معقد ، إلا أن الطريقة تظهر أحيانًا بشكل جيد عن طريق القفز بالحد الأدنى المحلي

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.]) 

هذا كل شيء مع النسب المنسق. خوارزميات الطرق المقدمة بسيطة للغاية ، لذلك ليس من الصعب تنفيذها. في المستقبل ، يمكنك التفكير في الأدوات المضمنة للغة جوليا ، لكن في الوقت الحالي تريد أن تشعر بكل شيء بيديك ، إذا جاز التعبير ، فكر في طرق أكثر تعقيدًا وفعالية ، ثم يمكنك الانتقال إلى التحسين العالمي ، مع المقارنة في نفس الوقت بالتنفيذ بلغة أخرى.

الأدب

1. Zaitsev V.V. الطرق العددية للفيزيائيين. المعادلات غير الخطية والتحسين: تعليمي. - سمارة ، 2005 - 86 ثانية.
2. Ivanov A.V. أساليب الكمبيوتر لتحسين النظم البصرية. دليل الدراسة. - SPB: SPbSU ITMO ، 2010 - 114 ثانية.
3. Popova T. M. طرق التحسين متعدد الأبعاد: إرشادات ومهام العمل في المختبر في مجال "طرق التحسين" للطلاب في اتجاه "الرياضيات التطبيقية" / شركات. تي إم بوبوفا. - خاباروفسك: دار النشر للمحيط الهادئ. الدولة الجامعة ، 2012 .-- 44 ص.