احتمال الفوز في مباراة مع احتمال معروف للفوز نقطة الثانية

إذا لم تقرأ مقالتي الأولى حول هذا الموضوع ، فإنني أنصحك أن تبدأ به .

بما أنني ذكرت موقفًا معينًا ، وإن كان غير مباشر للغاية ، لعلماء الرياضيات الماليين ، اسمحوا لي أن أطور الموضوع إلى حد العبث بناءً على كيفية تطويره في تحليلات المخاطر. عند حساب سعر أحد الخيارات ، فغالبًا ما يأخذون في الاعتبار حساسية هذا السعر لمجموعة من المعلمات. على سبيل المثال ، كيف سيتغير سعر الخيار عندما يتغير سعر السهم الذي صدر له الخيار ، أو عندما يتغير تقلب سعر السهم ، أو معدل البنك المركزي ، إلخ.

قد نكون مهتمين بكيفية تغير احتمال الفوز بلعبة ما عندما يتغير احتمال الفوز بنقطة ما. في الواقع ، نريد حساب المشتق من الأول إلى الثاني. أبسط طريقة هي تقييمها بالعين من الرسم البياني. يمكن ملاحظة أن الحد الأقصى يتحقق في حالة 50:50. إذا تغيرت احتمالات الفوز بنقطة ما من 0.45 إلى 0.55 ، فإن احتمال الفوز بتنس الريشة يزيد من 0.26 إلى 0.74 ، أي بمقدار 0.48. يعطي التقدير التقريبي مشتقًا في المنطقة 5. وهذا يعني ، إذا نمت إلى 0.51 (أي 51٪) مع فرص متساوية ، فإن الزيادة في احتمال الفوز باللعبة ستكون حوالي 0.05 (أو 5٪). وبالمثل ، يمكنك حساب المشتق في أي نقطة أخرى على الرسم البياني.

في التمويل ، عادةً ما يتم استخدام نهج "bump and run" ، أي أنها تغير المعلمة بمقدار صغير وتحسب سعر الخيار الجديد ومشتقاته. بعد أن تصرفت بطريقة مماثلة ، أقتبس البيانات الدقيقة على الرسم البياني (لقد أخذت التغيير بنسبة مئوية ، غير مهذب قليلاً ، لكن مقبول في هذا الموقف). لمزيد من الوضوح ، أضاف الألعاب ما يصل إلى 5 و 31 نقطة. بالمناسبة ، يمكن اعتبار إطلاق النار في البياتلون كطرف يصل إلى 5. ليس هذا تشبيهًا مطلقًا ، حيث تم إصلاح العدد الإجمالي للطلقات. لكن طرق الحل هي نفسها تقريبا.



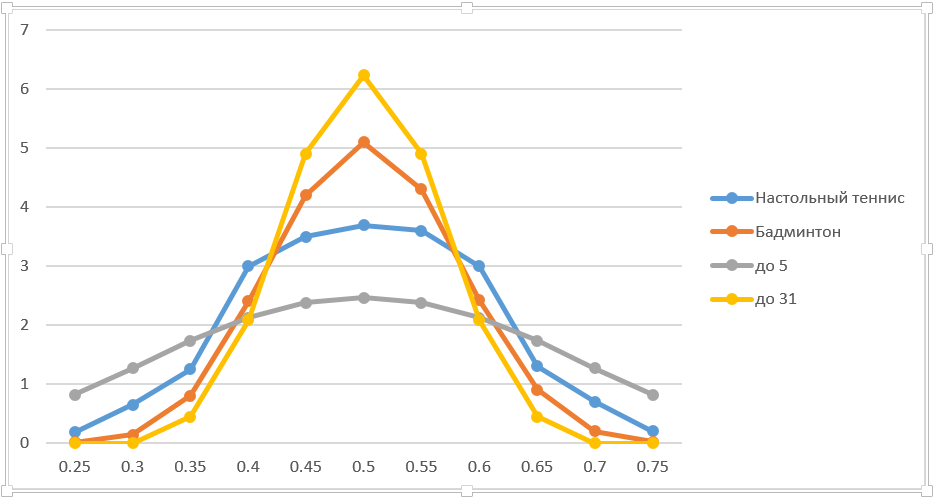
من الواضح أنه كلما طالت فترة الدفع ، ارتفع المشتق في 50:50. إذا كان طول الحفلة يميل إلى ما لا نهاية ، فمن الناحية العملية يكسب انتصار اللاعب الذي يتمتع بأقل ميزة. ينخفض ​​عرض المنحنى وفقًا لذلك. بشكل عام ، الاستنتاجات واضحة تمامًا.

يمكنك حساب حساسية التصريف العرضي لنقطة واحدة. على سبيل المثال ، تغذية في الشبكة. كم تؤثر قسيمة واحدة على نتيجة اللعبة؟ في الواقع ، هذا هو انخفاض في درجة الفوز للخصم بمقدار نقطة واحدة. الرسم البياني أدناه يعكس هذا الموقف. بطبيعة الحال ، في تنس الطاولة ، من المهم للغاية خسارة نقطة من لعبة تنس الريشة. مع القوى المتساوية ، ينخفض ​​احتمال نتائج اللعبة قدر الإمكان - من 0.5 إلى 0.41. انتبه إلى عدم تناسق المنحنيات (على عكس معظم الآخرين). هذه ليست صدفة. الحقيقة هي أن الرصيد ينتقل من 50:50 إلى احتمال أعلى للفوز بنقطة ما ، لأن النقطة المفقودة تزيد من فرص اللاعب.



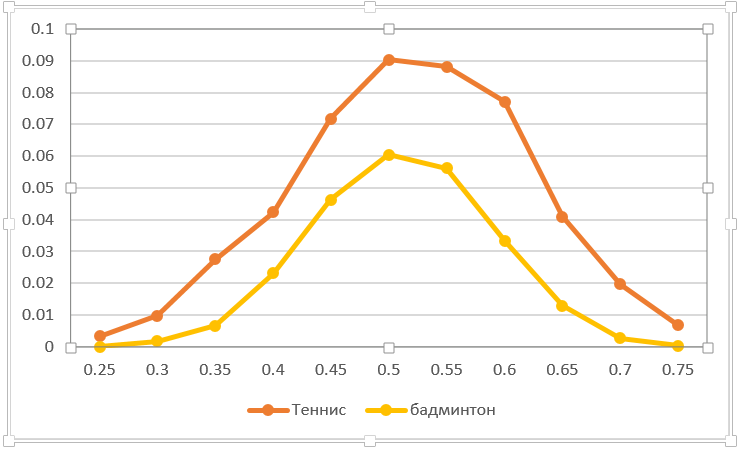
دعونا نضع تجربة أخرى مثيرة للاهتمام. تخيل أن أحد اللاعبين يمكنه التركيز ولعب 3 نقاط أعلى من المتوسط ​​(p1 + دلتا). افترض أنه بعد ذلك ، ستعود المحاذاة إلى الأصل (إلى المتوسط ​​المتوقع دون مراعاة "زيادة القوة"). من الواضح أن احتمال الفوز سيزداد. السؤال هو ، هل يهم متى يجب التركيز - في بداية اللعبة أم في نهايتها؟ أقترح القيام افتراض قبل قراءة المزيد.



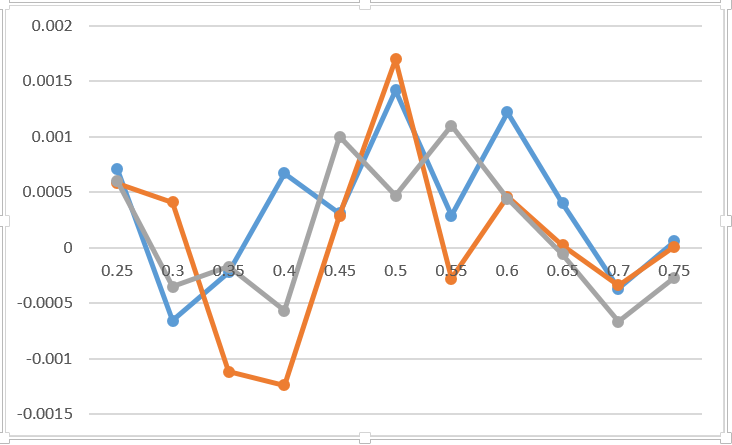
لذلك ، كما توضح التجربة ، ليس هناك فرق على الإطلاق عند التركيز بالضبط (لا تؤخذ عوامل الخطة الأخلاقية في الاعتبار). يوضح الرسم البياني الفرق بين احتمال الفوز باللعبة في حالة التركيز في 3 أماكن مختلفة من اللعبة مقارنة بالتركيز على أول 3 نقاط. أعتقد أن هذا الرسم البياني يعكس خطأ مونت كارلو وليس أكثر. أضفت 0.2 إلى نتيجة التعادل نقطة للاعب الأول لمدة ثلاثة تعادلات. لا أشير حتى على الرسم البياني إلى السطر الذي يتوافق مع أي خيار. بالتأكيد لا يغير شيئا. النصيحة القيمة الوحيدة بشأن هذا الموضوع هي الاستعداد قبل فوات الأوان.

الآن لننظر في ما سيحدث إذا كان أحد اللاعبين لديه الاستقرار. الأعصاب هي أعصاب ، تحدث لعبة مسؤولة. لنفترض ، في المتوسط ​​، أنه يكسب نفس النسبة المئوية من النقاط ، ولكن عند رسم نقطة محددة ، تطفو هذه النسبة. على سبيل المثال ، يتم لعب نصف النقاط باحتمال p1 + delta ، والنصف الآخر مع p1-delta. في هذه الحالة ، يظل متوسط ​​p1 هو الأصلي ، ويحدث فقدان + دلتا أو دلتا عشوائيًا مع احتمال 0.5. هل ستؤثر بطريقة ما على نتيجة اللعبة؟ كما أوضحت تجاربي بمساعدة مونتي كارلو ، لا يمكن تتبع الفرق عمليا. في الواقع ، عند إضافة مبلغ معين أو طرحه ، وإن كان بشكل عشوائي ، فإننا نظل في نفس الاحتمال المتوسط ​​للفوز بنقطة ما. يشير الاقتراح إلى أن منحنى التوزيع لا يؤثر على نتيجة اللعبة ، ولكن فقط على المتوسط ​​، لكنني لن أتحملها بنفسي. هنا عليك أن تفكر.

أود أيضًا استنباط معادلة تفاضلية ، مثل Black Scholes في التمويل ، لإكمال الارتباط. حدد المشتقات المهمة ، وقم بالتخلص من المكون العشوائي ... نحتاج أيضًا إلى التعامل مع السلطة التقديرية. ربما سأترك هذا لعالم الرياضيات الحقيقي.